3.3 解一元一次方程(二)——去括号与去分母(2) 课件(共23张PPT)
文档属性
| 名称 | 3.3 解一元一次方程(二)——去括号与去分母(2) 课件(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-08 17:52:30 | ||
图片预览








文档简介
(共23张PPT)
3.3 解一元一次方程(二)
——去括号与去分母(2)
人教版 七年级上册
教学目标
教学目标:
1.掌握含有括号的一元一次方程的解法;
2.经历运用方程解决实际问题的过程,进一步体会方程模型的作用。
重点:含有括号的一元一次方程的解法是重点;
难点:括号前面是负号时去括号是难点。
新知导入
1.化简下列式子:
解:原式=
解:原式=
思考:如果要解 ,你能想到什么办法吗?
新知导入
英国伦敦博物馆保存着一部极其珍贵的文物——纸草书.这是古代埃及人用象形文字写在一种用纸莎草压制成的草片上的著作,它于公元前1700年左右写成.这部书中记载了许多有关数学的问题.
数学小史料
问题:一个数,它的三分之二,它的一半,它的七分之一,它的全部,加起来总共是33,求这个数.
思考:(1)题中涉及到哪些数量关系和相等关系?
(2)引进什么样的未知数,根据这样的相等关系列出方程?
分析:设这个数为x.
根据题意,得
此方程与上两节学的一元一次方程有何差异
能不能用上节课学过的去括号的方法求解?
该怎么求方程解呢
合作探究
合作探究
方法1:
合并同类项,得
系数化为1,得
方法2:
方程两边同乘各分母的最小公倍数42,得
合并同类项,得
系数化为1,得
这样做的依据是什么
思考:
两种解法有什么不同?你认为哪种解法比较简便?
等式的基本性质2.
97x=1386
合作探究
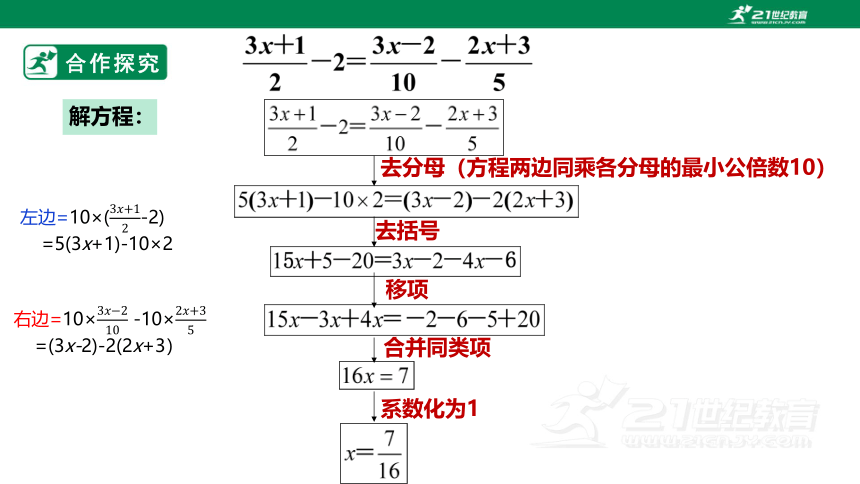
解方程:
去分母(方程两边同乘各分母的最小公倍数10)
去括号
移项
合并同类项
系数化为1
左边=10×(-2)
=5(3x+1)-10×2
右边=10× -10×
=(3x-2)-2(2x+3)
新知讲解
解含有分母的一元一次方程时,方程两边乘各分母的最小公倍数,从而约去分母,这个过程叫做去分母.
注意: (1) 去分母时,方程两边的每一项都要乘各分母的最小公倍数,不要漏乘没有分母的项;
(2) 由于分数线具有括号的作用,因此若分子是多项式,则去分母时,要将分子作为一个整体加上括号.
归纳总结
解一元一次方程的一般步骤和根据是:
(1)去分母(根据等式的性质2);
(2) 去括号(根据分配律);
(3) 移项 (根据等式性质1);
(4)合并同类项(逆用分配律);
(5)化系数为1,得到方程的解(根据等式性质2).
例题讲解
例3 解下列方程:
解:去分母(方程两边乘4),得
2(x + 1) – 4 = 8 +(2 – x).
去括号,得 2x + 2 – 4 = 8 + 2 – x.
移项,得 2x + x = 8 + 2 – 2 + 4 .
合并同类项,得 3x = 12.
系数化为1,得 x = 4.
例题讲解
解:去分母(方程两边乘6),得
18x + 3(x – 1)= 18 – 2(2x – 1)
去括号,得 18x + 3x – 3 = 18 – 4x + 2
移项,得 18x + 3x +4x = 18 + 2 + 3
合并同类项,得 25x = 23
系数化为1,得
针对训练
下列方程的解法对不对?如果不对,你能找出错在哪里吗?
解方程:
解:去分母,得 4x-1-3x + 6 = 1
移项,合并同类项,得 x=4
方程右边的“1”去分母时漏乘最小公倍数6
去括号符号错误
约去分母3后,(2x-1)×2在去括号时出错
课堂练习
1.以下解方程 的过程中,从哪一步开始出现错误( )
A.4(2y-1)-2(5y+2)=3(3y+1)-1
B.8y-4-10y-4=9y+3-1
C.-11y=10
D.y=-
A
课堂练习
2. 把方程 去分母,正确的是( )
A.18x+2(2x-1)=18-3(x+1)
B.3x+2(2x-1)=3-3(x+1)
C.18x+(2x-1)=18-(x+1)
D.18x+4x-1=18-3x+1
A
课堂练习
4.某书中一道解方程题 ,▲处印刷时被墨盖住了,查后面答案,发现这道题的解为x=-2.5,那么▲处的数字为 .
3.若关于x的一元一次方程 的解是x=-1,则k的值是( )
A.27 B.1 C.- D.0
B
5
课堂练习
5. 下面是解方程 的过程,请在前面的括号内填写变形步骤,在后面的括号内填写变形依据.
解:去分母,得3(3x+5)=2(2x-1).( )
去括号,得9x+15=4x-2.( )
( ),得9x-4x=-15-2.( )
( ),得5x=-17.
( ),得 ( )
等式的性质2
去括号法则
移项
等式的性质1
合并同类项
系数化为1
等式的性质2
课堂练习
6.解下列方程:
去括号,得2x-2-x-2=12-3x.
移项,得2x-x+3x=2+2+12.
合并同类项,得4x=16.
系数化为1,得x=4;
解:去分母,得2(x-1)-(x+2)=3(4-x).
课堂练习
6.解下列方程:
去括号,得3x-x+1=6x-2.
移项,得3x-x-6x=-2-1.
合并同类项,得-4x=-3.
系数化为1,得x= ;
去分母,得3x-(x-1)=6x-2.
解:原方程可化为
课堂练习
7. 当x为何值时,代数式2(x2-1)-x2的值比代数式
x2+3x-2的值大6.
解:依题意得 2( x2-1 )-x2-( x2+3x-2 ) =6,
去括号,得2x2-2-x2-x2-3x+2=6,
移项、合并同类项,得-3x=6,
系数化为1,得x=-2.
课堂练习
8. 某单位计划“五一”期间组织职工到东江湖旅游,如果单独租用40座的客车若干辆刚好坐满;如果租用50座的客车则可以少租一辆,并且有40个剩余座位.该单位参加旅游的职工有多少人?
解:设该单位参加旅游的职工有x人,由题意得方程:
解得 x=360.
答:该单位参加旅游的职工有360人.
课堂总结
解一元一次
方程的步骤
移项
合并同类项
系数化为1
去括号
去分母
2. 分子是多项式应添括号
1.不要漏乘不含分母的项
2.括号前是“-”号,要变号
1.不要漏乘括号中的每一项
移项要变号
系数相加,不漏项
分子、分母不要写倒了
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
3.3 解一元一次方程(二)
——去括号与去分母(2)
人教版 七年级上册
教学目标
教学目标:
1.掌握含有括号的一元一次方程的解法;
2.经历运用方程解决实际问题的过程,进一步体会方程模型的作用。
重点:含有括号的一元一次方程的解法是重点;
难点:括号前面是负号时去括号是难点。
新知导入
1.化简下列式子:
解:原式=
解:原式=
思考:如果要解 ,你能想到什么办法吗?
新知导入
英国伦敦博物馆保存着一部极其珍贵的文物——纸草书.这是古代埃及人用象形文字写在一种用纸莎草压制成的草片上的著作,它于公元前1700年左右写成.这部书中记载了许多有关数学的问题.
数学小史料
问题:一个数,它的三分之二,它的一半,它的七分之一,它的全部,加起来总共是33,求这个数.
思考:(1)题中涉及到哪些数量关系和相等关系?
(2)引进什么样的未知数,根据这样的相等关系列出方程?
分析:设这个数为x.
根据题意,得
此方程与上两节学的一元一次方程有何差异
能不能用上节课学过的去括号的方法求解?
该怎么求方程解呢
合作探究
合作探究
方法1:
合并同类项,得
系数化为1,得
方法2:
方程两边同乘各分母的最小公倍数42,得
合并同类项,得
系数化为1,得
这样做的依据是什么
思考:
两种解法有什么不同?你认为哪种解法比较简便?
等式的基本性质2.
97x=1386
合作探究
解方程:
去分母(方程两边同乘各分母的最小公倍数10)
去括号
移项
合并同类项
系数化为1
左边=10×(-2)
=5(3x+1)-10×2
右边=10× -10×
=(3x-2)-2(2x+3)
新知讲解
解含有分母的一元一次方程时,方程两边乘各分母的最小公倍数,从而约去分母,这个过程叫做去分母.
注意: (1) 去分母时,方程两边的每一项都要乘各分母的最小公倍数,不要漏乘没有分母的项;
(2) 由于分数线具有括号的作用,因此若分子是多项式,则去分母时,要将分子作为一个整体加上括号.
归纳总结
解一元一次方程的一般步骤和根据是:
(1)去分母(根据等式的性质2);
(2) 去括号(根据分配律);
(3) 移项 (根据等式性质1);
(4)合并同类项(逆用分配律);
(5)化系数为1,得到方程的解(根据等式性质2).
例题讲解
例3 解下列方程:
解:去分母(方程两边乘4),得
2(x + 1) – 4 = 8 +(2 – x).
去括号,得 2x + 2 – 4 = 8 + 2 – x.
移项,得 2x + x = 8 + 2 – 2 + 4 .
合并同类项,得 3x = 12.
系数化为1,得 x = 4.
例题讲解
解:去分母(方程两边乘6),得
18x + 3(x – 1)= 18 – 2(2x – 1)
去括号,得 18x + 3x – 3 = 18 – 4x + 2
移项,得 18x + 3x +4x = 18 + 2 + 3
合并同类项,得 25x = 23
系数化为1,得
针对训练
下列方程的解法对不对?如果不对,你能找出错在哪里吗?
解方程:
解:去分母,得 4x-1-3x + 6 = 1
移项,合并同类项,得 x=4
方程右边的“1”去分母时漏乘最小公倍数6
去括号符号错误
约去分母3后,(2x-1)×2在去括号时出错
课堂练习
1.以下解方程 的过程中,从哪一步开始出现错误( )
A.4(2y-1)-2(5y+2)=3(3y+1)-1
B.8y-4-10y-4=9y+3-1
C.-11y=10
D.y=-
A
课堂练习
2. 把方程 去分母,正确的是( )
A.18x+2(2x-1)=18-3(x+1)
B.3x+2(2x-1)=3-3(x+1)
C.18x+(2x-1)=18-(x+1)
D.18x+4x-1=18-3x+1
A
课堂练习
4.某书中一道解方程题 ,▲处印刷时被墨盖住了,查后面答案,发现这道题的解为x=-2.5,那么▲处的数字为 .
3.若关于x的一元一次方程 的解是x=-1,则k的值是( )
A.27 B.1 C.- D.0
B
5
课堂练习
5. 下面是解方程 的过程,请在前面的括号内填写变形步骤,在后面的括号内填写变形依据.
解:去分母,得3(3x+5)=2(2x-1).( )
去括号,得9x+15=4x-2.( )
( ),得9x-4x=-15-2.( )
( ),得5x=-17.
( ),得 ( )
等式的性质2
去括号法则
移项
等式的性质1
合并同类项
系数化为1
等式的性质2
课堂练习
6.解下列方程:
去括号,得2x-2-x-2=12-3x.
移项,得2x-x+3x=2+2+12.
合并同类项,得4x=16.
系数化为1,得x=4;
解:去分母,得2(x-1)-(x+2)=3(4-x).
课堂练习
6.解下列方程:
去括号,得3x-x+1=6x-2.
移项,得3x-x-6x=-2-1.
合并同类项,得-4x=-3.
系数化为1,得x= ;
去分母,得3x-(x-1)=6x-2.
解:原方程可化为
课堂练习
7. 当x为何值时,代数式2(x2-1)-x2的值比代数式
x2+3x-2的值大6.
解:依题意得 2( x2-1 )-x2-( x2+3x-2 ) =6,
去括号,得2x2-2-x2-x2-3x+2=6,
移项、合并同类项,得-3x=6,
系数化为1,得x=-2.
课堂练习
8. 某单位计划“五一”期间组织职工到东江湖旅游,如果单独租用40座的客车若干辆刚好坐满;如果租用50座的客车则可以少租一辆,并且有40个剩余座位.该单位参加旅游的职工有多少人?
解:设该单位参加旅游的职工有x人,由题意得方程:
解得 x=360.
答:该单位参加旅游的职工有360人.
课堂总结
解一元一次
方程的步骤
移项
合并同类项
系数化为1
去括号
去分母
2. 分子是多项式应添括号
1.不要漏乘不含分母的项
2.括号前是“-”号,要变号
1.不要漏乘括号中的每一项
移项要变号
系数相加,不漏项
分子、分母不要写倒了
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
