2022-2023学年冀教版八年级数学上册13.3.3利用ASA和AAS判定 课件(共24张PPT)
文档属性
| 名称 | 2022-2023学年冀教版八年级数学上册13.3.3利用ASA和AAS判定 课件(共24张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-08 20:59:39 | ||
图片预览





文档简介
(共24张PPT)
第十三章 全等三角形
13.3.3 利用"asa"和"aas"判定
两个三角形全等
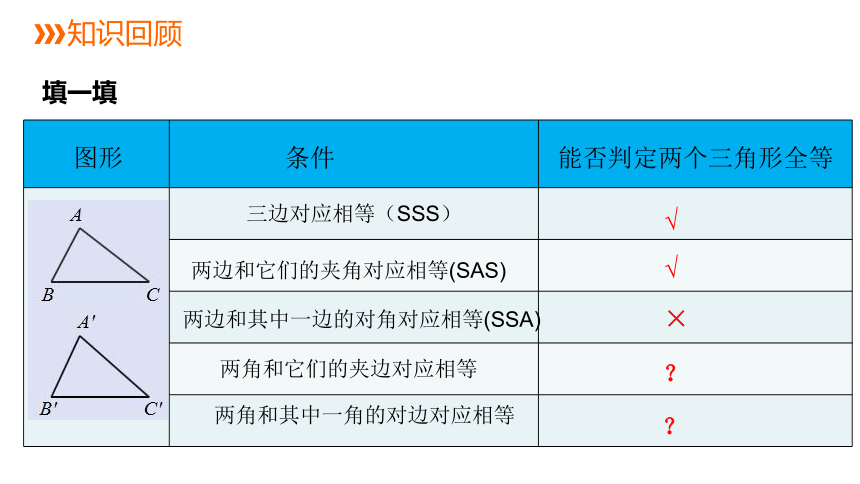
三边对应相等(SSS)
图形
条件
能否判定两个三角形全等
√
√
×
?
?
知识回顾
填一填
两边和它们的夹角对应相等(SAS)
两边和其中一边的对角对应相等(SSA)
两角和其中一角的对边对应相等
两角和它们的夹边对应相等
1.掌握三角形全等的判定方法:“ASA”和“AAS”.
2.能够运用“ASA”和“AAS”证明两个三角形全等.
3.会利用三角形全等的性质,证明线段、角相等.
学习目标
重点:掌握三角形全等的判定方法:“ASA”和“AAS”.
难点:能利用“ASA”和“AAS”解决相关的实际问题.
重点难点
认真阅读课本44页“一起探究”,并完成下列问题 :
1.动手作△ABC,要求:∠A=40°,∠B=60°,AB=10cm.
时间:3分钟,完成的同学请举手!
自学指导
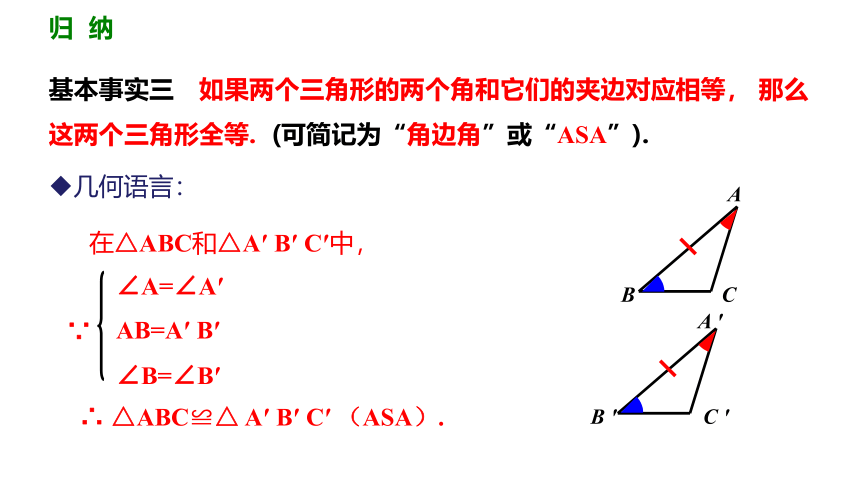
基本事实三 如果两个三角形的两个角和它们的夹边对应相等, 那么这两个三角形全等. (可简记为“角边角”或“ASA”).
归 纳
几何语言:
∠A=∠A′
AB=A′ B′
∠B=∠B′
在△ABC和△A′ B′ C′中,
∴ △ABC≌△ A′ B′ C′ (ASA).
A
B
C
A ′
B ′
C ′
∵
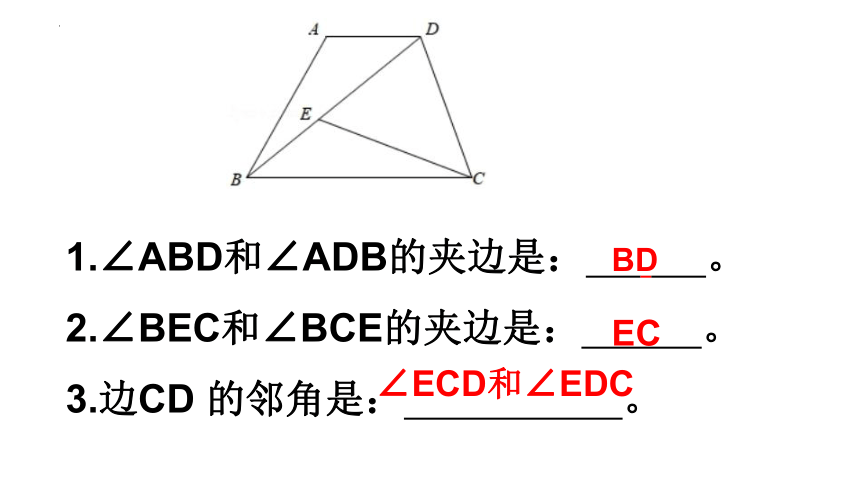
1.∠ABD和∠ADB的夹边是: 。
2.∠BEC和∠BCE的夹边是: 。
3.边CD 的邻角是: 。
BD
EC
∠ECD和∠EDC
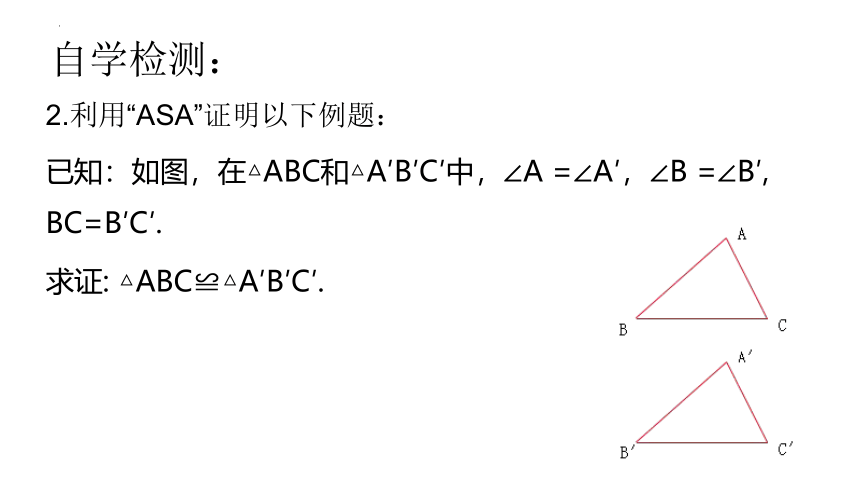
2.利用“ASA”证明以下例题:
已知:如图,在△ABC和△A′B′C′中,∠A =∠A′,∠B =∠B′, BC=B′C′.
求证: △ABC≌△A′B′C′.
3.完成P46例2,注意解题的格式方法和步骤。
时间:9 分钟,请注意坐姿端正,书写规范
自学检测:
证明:∵∠A+∠B+∠C=180°,∠A′+∠B′+∠C′=180°,
∴∠C=180°-∠A-∠B,∠C′=180°-∠A′- ∠B′
又∵ ∠A=∠A′,∠B=∠B′,
∴∠C=∠C′
∴ΔABC≌ΔA′B′C′(ASA)
在ΔABC和ΔA′B′C′中,
2:已知:如图,在△ABC和△A′B′C′中,∠A =∠A′,∠B =∠B′, BC=B′C′.求证: △ABC≌△A′B′C′.
判定定理:如果两个三角形的两角和其中一个角的对边对应相等,那么这两个三角形全等(简记为“角角边”或“AAS”)
几何语言:
在△ABC 和△ A′B′ C′中
∴ △ABC ≌△ A′B′ C′(AAS).
归纳
∠A =∠A′
∠C =∠C′
CB = C′B′
∵
在△ABC 和△ A′B′ C′中
∠A =∠A′
∠C =∠C′
CB = C′B′
∵
后教:
例1 如图,AD∥BC,BE∥DF,AE=CF,
求证:△ADF≌△CBE.
解析:根据平行线的性质可得∠A=∠C,∠DFE=∠BEC,再根据等式的性质可得AF=CE,然后利用ASA可证明△ADF≌△CBE.
∴△ADF≌△CBE(ASA).
∠DFA=∠BEC,
∵AE=CF,
∴AE+EF=CF+EF,即AF=CE.
在△ADF和△CBE中,
AF=CE,
∠A=∠C,
证明:∵AD∥BC,BE∥DF,
∴∠A=∠C,∠DFE=∠BEC.
∵
例2 如图,CA=CD,∠B=∠E,∠BCE= ∠ACD.
求证:AB=DE.
解析:由∠BCE=∠ACD推出∠BCA=∠ECD,然后由已知条件CA=CD,∠B=∠E,即利用AAS可得出△ABC≌△DEC,即可得出AB=DE.
证明:∵∠BCE=∠ACD,
∴∠BCE+∠ACE=∠ACD+∠ACE,
即∠BCA=∠ECD.
在△ABC和△DEC中,
∠B=∠E
∵ ∠BCA=∠ECD
CA=CD
∴△ABC≌△DEC(AAS).
∴AB=DE.
例3 如图,在△ABC中,AD⊥BC于点D,BE⊥AC于E.AD与BE交于F,若BF=AC,
求证:△ADC≌△BDF.
解析:先证明∠ADC=∠BDF,∠DAC=∠DBF,再由BF=AC,根据AAS即可得出两三角形全等.
∴△ADC≌△BDF(AAS).
AC=BF,
∠ADC=∠BDF,
思路1:证明:∵AD⊥BC,BE⊥AC,
∴∠ADC=∠BEC=90°.
∴∠C+∠CBE=90°,∠C+∠DAC=90°
∴∠DAC=∠CBE
在△ADC和△BDF中,
∠DAC=∠DBF,
思路2:∵∠CBE+∠C=90°,∠CBE+∠BFD=90°
∴∠C=∠BFD.
思路3:∵∠AFE=∠BFD,∠AEF=∠BDF=90°
在△AFE和△BFD中,
∴∠DAC=∠DBF
1.已知一边及其邻角对应相等
2.已知一边及其对角对应相等
3.已知两角对应相等
“AAS”
“ASA”
“SAS”
“AAS”
“ASA”
“AAS”
“AAS”
“ASA”
“SAS”
“AAS”
“AAS”
“ASA”
“SAS”
“AAS”
“ASA”
“SAS”
证明三角形全等的思路:
思路一:已知两边对应相等
通常采取下列方法:①找两边的夹角,利用“SAS”证明两个三角形全等;
②找第三边,利用“SSS”证明两个三角形全等.
思路二:已知一边及其邻角对应相等
当已知一边及其邻角对应相等时:
①找任意角,利用“AAS”或“ASA”证明两个三角形全等;
②找夹这个角的另一条边,利用“SAS”证明两个三角形全等.
注意:切记不能用“SSA”证明两个三角形全等.
思路三 已知一边及其对角对应相等
当已知一边及其对角对应相等时,找任意角,利用“AAS”证明两个三角形全等.
思路四 已知两角对应相等
当已知两角对应相等时,通常采取下列方法:
①找其中任意一角的对边,利用“AAS”证明两个三角形全等;
②找两角的夹边,利用“ASA”证明两个三角形全等.
例4:已知:如图,AB,CD相交于点O.OA=OD.要使ΔOAC≌ΔODB.还需要添加一个条件,这个条件是什么?
课堂小结
全等三角形的判定(3)
应用
事实
定理
有两角及其中一个角的对边对应相等的两个三角形全等.
(简记为“角角边”或 “AAS”)
有两角及夹边对应相等的两个三角形全等.(简记为“角边角”或 “ASA”)
为证明线段和角的相等提供了新的方法
完成导学案堂清作业。
下课上交,看谁完成的又对又快!
请注意坐姿端正,书写规范!
堂清作业
感谢各位老师的聆听,
请大家批评指正!
第十三章 全等三角形
13.3.3 利用"asa"和"aas"判定
两个三角形全等
三边对应相等(SSS)
图形
条件
能否判定两个三角形全等
√
√
×
?
?
知识回顾
填一填
两边和它们的夹角对应相等(SAS)
两边和其中一边的对角对应相等(SSA)
两角和其中一角的对边对应相等
两角和它们的夹边对应相等
1.掌握三角形全等的判定方法:“ASA”和“AAS”.
2.能够运用“ASA”和“AAS”证明两个三角形全等.
3.会利用三角形全等的性质,证明线段、角相等.
学习目标
重点:掌握三角形全等的判定方法:“ASA”和“AAS”.
难点:能利用“ASA”和“AAS”解决相关的实际问题.
重点难点
认真阅读课本44页“一起探究”,并完成下列问题 :
1.动手作△ABC,要求:∠A=40°,∠B=60°,AB=10cm.
时间:3分钟,完成的同学请举手!
自学指导
基本事实三 如果两个三角形的两个角和它们的夹边对应相等, 那么这两个三角形全等. (可简记为“角边角”或“ASA”).
归 纳
几何语言:
∠A=∠A′
AB=A′ B′
∠B=∠B′
在△ABC和△A′ B′ C′中,
∴ △ABC≌△ A′ B′ C′ (ASA).
A
B
C
A ′
B ′
C ′
∵
1.∠ABD和∠ADB的夹边是: 。
2.∠BEC和∠BCE的夹边是: 。
3.边CD 的邻角是: 。
BD
EC
∠ECD和∠EDC
2.利用“ASA”证明以下例题:
已知:如图,在△ABC和△A′B′C′中,∠A =∠A′,∠B =∠B′, BC=B′C′.
求证: △ABC≌△A′B′C′.
3.完成P46例2,注意解题的格式方法和步骤。
时间:9 分钟,请注意坐姿端正,书写规范
自学检测:
证明:∵∠A+∠B+∠C=180°,∠A′+∠B′+∠C′=180°,
∴∠C=180°-∠A-∠B,∠C′=180°-∠A′- ∠B′
又∵ ∠A=∠A′,∠B=∠B′,
∴∠C=∠C′
∴ΔABC≌ΔA′B′C′(ASA)
在ΔABC和ΔA′B′C′中,
2:已知:如图,在△ABC和△A′B′C′中,∠A =∠A′,∠B =∠B′, BC=B′C′.求证: △ABC≌△A′B′C′.
判定定理:如果两个三角形的两角和其中一个角的对边对应相等,那么这两个三角形全等(简记为“角角边”或“AAS”)
几何语言:
在△ABC 和△ A′B′ C′中
∴ △ABC ≌△ A′B′ C′(AAS).
归纳
∠A =∠A′
∠C =∠C′
CB = C′B′
∵
在△ABC 和△ A′B′ C′中
∠A =∠A′
∠C =∠C′
CB = C′B′
∵
后教:
例1 如图,AD∥BC,BE∥DF,AE=CF,
求证:△ADF≌△CBE.
解析:根据平行线的性质可得∠A=∠C,∠DFE=∠BEC,再根据等式的性质可得AF=CE,然后利用ASA可证明△ADF≌△CBE.
∴△ADF≌△CBE(ASA).
∠DFA=∠BEC,
∵AE=CF,
∴AE+EF=CF+EF,即AF=CE.
在△ADF和△CBE中,
AF=CE,
∠A=∠C,
证明:∵AD∥BC,BE∥DF,
∴∠A=∠C,∠DFE=∠BEC.
∵
例2 如图,CA=CD,∠B=∠E,∠BCE= ∠ACD.
求证:AB=DE.
解析:由∠BCE=∠ACD推出∠BCA=∠ECD,然后由已知条件CA=CD,∠B=∠E,即利用AAS可得出△ABC≌△DEC,即可得出AB=DE.
证明:∵∠BCE=∠ACD,
∴∠BCE+∠ACE=∠ACD+∠ACE,
即∠BCA=∠ECD.
在△ABC和△DEC中,
∠B=∠E
∵ ∠BCA=∠ECD
CA=CD
∴△ABC≌△DEC(AAS).
∴AB=DE.
例3 如图,在△ABC中,AD⊥BC于点D,BE⊥AC于E.AD与BE交于F,若BF=AC,
求证:△ADC≌△BDF.
解析:先证明∠ADC=∠BDF,∠DAC=∠DBF,再由BF=AC,根据AAS即可得出两三角形全等.
∴△ADC≌△BDF(AAS).
AC=BF,
∠ADC=∠BDF,
思路1:证明:∵AD⊥BC,BE⊥AC,
∴∠ADC=∠BEC=90°.
∴∠C+∠CBE=90°,∠C+∠DAC=90°
∴∠DAC=∠CBE
在△ADC和△BDF中,
∠DAC=∠DBF,
思路2:∵∠CBE+∠C=90°,∠CBE+∠BFD=90°
∴∠C=∠BFD.
思路3:∵∠AFE=∠BFD,∠AEF=∠BDF=90°
在△AFE和△BFD中,
∴∠DAC=∠DBF
1.已知一边及其邻角对应相等
2.已知一边及其对角对应相等
3.已知两角对应相等
“AAS”
“ASA”
“SAS”
“AAS”
“ASA”
“AAS”
“AAS”
“ASA”
“SAS”
“AAS”
“AAS”
“ASA”
“SAS”
“AAS”
“ASA”
“SAS”
证明三角形全等的思路:
思路一:已知两边对应相等
通常采取下列方法:①找两边的夹角,利用“SAS”证明两个三角形全等;
②找第三边,利用“SSS”证明两个三角形全等.
思路二:已知一边及其邻角对应相等
当已知一边及其邻角对应相等时:
①找任意角,利用“AAS”或“ASA”证明两个三角形全等;
②找夹这个角的另一条边,利用“SAS”证明两个三角形全等.
注意:切记不能用“SSA”证明两个三角形全等.
思路三 已知一边及其对角对应相等
当已知一边及其对角对应相等时,找任意角,利用“AAS”证明两个三角形全等.
思路四 已知两角对应相等
当已知两角对应相等时,通常采取下列方法:
①找其中任意一角的对边,利用“AAS”证明两个三角形全等;
②找两角的夹边,利用“ASA”证明两个三角形全等.
例4:已知:如图,AB,CD相交于点O.OA=OD.要使ΔOAC≌ΔODB.还需要添加一个条件,这个条件是什么?
课堂小结
全等三角形的判定(3)
应用
事实
定理
有两角及其中一个角的对边对应相等的两个三角形全等.
(简记为“角角边”或 “AAS”)
有两角及夹边对应相等的两个三角形全等.(简记为“角边角”或 “ASA”)
为证明线段和角的相等提供了新的方法
完成导学案堂清作业。
下课上交,看谁完成的又对又快!
请注意坐姿端正,书写规范!
堂清作业
感谢各位老师的聆听,
请大家批评指正!
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
