数学人教A版(2019)选择性必修第一册2.3.1两条直线的交点坐标(共21张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第一册2.3.1两条直线的交点坐标(共21张ppt) | 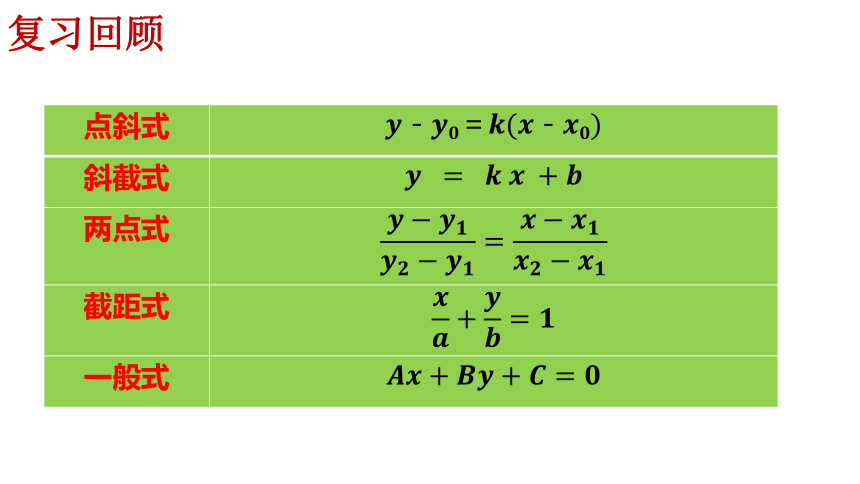 | |
| 格式 | zip | ||
| 文件大小 | 934.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-08 20:44:03 | ||
图片预览
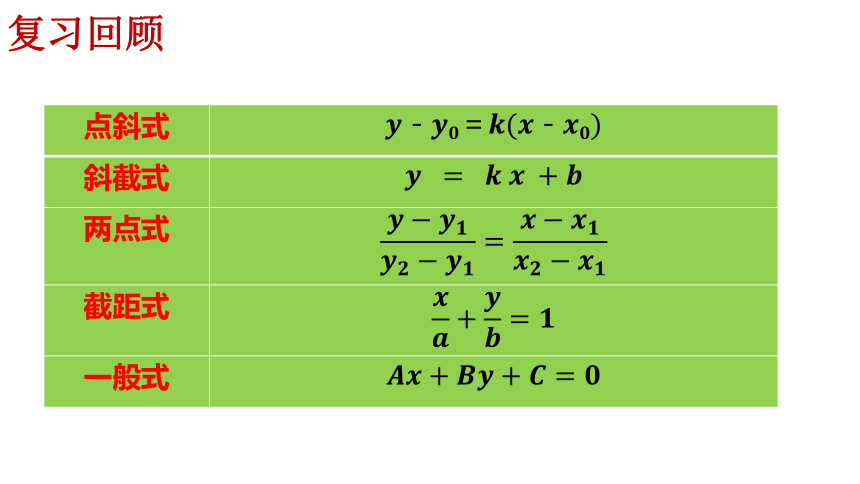






文档简介
(共21张PPT)
复习回顾
点斜式
斜截式
两点式
截距式
一般式
第二章 直线和圆的方程
2.3 直线的交点坐标与距离公式
课时1 两条直线的交点坐标
1.会用解方程组的方法求两条相交直线的交点坐标.(数学运算)
2.会根据方程解的个数判定两条直线的位置关系.(直观想象)
几何元素及关系 代数表示
点A
直线l
点A在直线l上
直线l1与l2的交点是A
A的坐标满足方程
A的坐标是方程组
一、两条直线的交点
做一做:
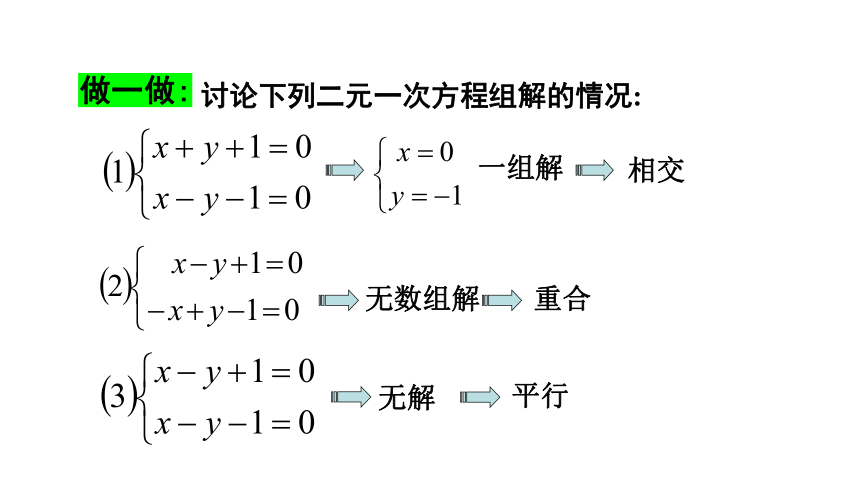
讨论下列二元一次方程组解的情况:
无数组解
无解
重合
平行
一组解
相交
两条直线的交点坐标是下列方程组的解
(1)联立
(2)求解
(3)得交点
(1)若方程组有且只有一个解,
(2)若方程组无解,
(3)若方程组有无数解,
则l1// l2;
则l1与l2相交;
则l1与l2重合.
两条直线的交点的分类:
*结论:
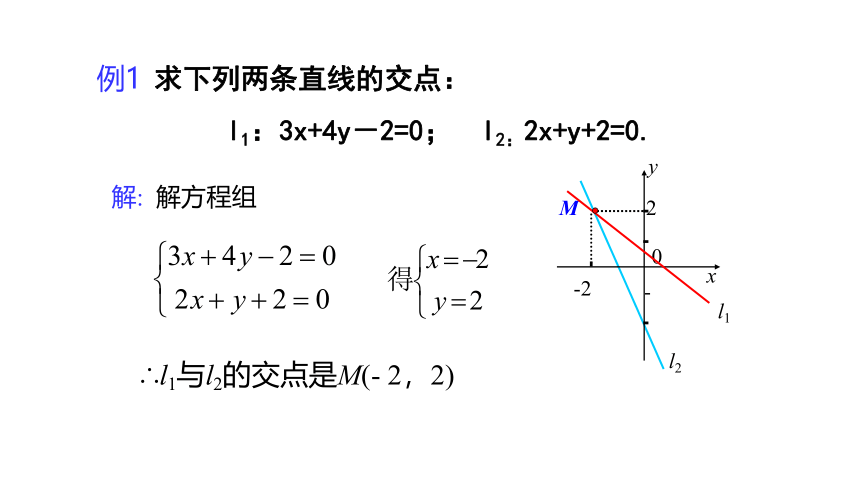
求下列两条直线的交点:
l1:3x+4y-2=0; l2:2x+y+2=0.
解: 解方程组
∴l1与l2的交点是M(- 2,2)
x
y
M
-2
2
0
l1
l2
例1
例2:判定下列各对直线的位置关系,若相交,则求交点的坐标
(1)
解:解方程组
得
所以直线l1与l2相交,交点是
例题分析:例 2(1)
另一方面,
(2)
另一方面,
无解
所以 l1 // l2
所以直线 l1 与 l2 无公共点,l1 // l2
解:解方程组
例题分析:例 2(2)
(3)
∴直线l1与l2重合
解: ∵
∴直线l1与l2的方程可化为同一个方程
∴直线l1与l2的方程表示同一条直线
例题分析: 例 2(3)
用斜率判断和通过解方程组判断这两种方法都是通过代数方法研究两条直线的位置关系.用斜率容易判断两条直线平行或相交(或垂直),但无法直接得出相交时两条直线的交点坐标.
还有其他方法吗?
画图!画出直线
新知运用
例1 求过直线
拓展:直线系方程
一般地,具有某种共同属性的一类直线的集合称为直线系,它的方程叫作直线系方程。直线系方程中除含变量x,y以外,还有根据具体条件取不同值的变量,称为参变量,简称参数。由于参数的属性及取法不同,故可得到不同的直线系。根据直线系的属性,常见的直线系有:
(1)共点直线系方程:经过直线l1:,l2: 交点的直线系方程为:
①(,为参变量,且,不同时为0)
②(为待定的系数)
=0时,方程为3x+4y-2=0
x
y
=1时,方程为5x+5y=0
=-1时,方程为x+3y-4=0
O
上式整理为:(3+2λ)x+(4+λ)y+2λ-2=0
几何意义: 此方程表示经过直线3x+4y-2=0与直线2x+y+2=0 交点的直线集合(直线束).
共点直线系方程
(2)平行直线系方程:与直线平行的直线系方程为
(为参变量,且
(3)垂直直线系方程:与直线垂直的直线系方程为
(为参变量
例1用直线系方程解
例1 求过直线
所以直线的方程为:
解: (1) 设经过二直线交点的直线方程为:
巩固练习
求过两直线x-2y+4=0和x+y-2=0的交点,且满足下列条件的直线l的方程.
(1)过点(2,1);
(2)和直线3x-4y+5=0垂直;
(3)和直线2x-y+6=0平行.
∵直线l过点(2,1)
解: (2) 设经过二直线交点的直线方程为:
所以直线的方程为:
∵直线l和直线3x-4y+5=0垂直
求过两直线x-2y+4=0和x+y-2=0的交点,且满足下列条件的直线l的方程.
(1)过点(2,1);
(2)和直线3x-4y+5=0垂直;
(3)和直线2x-y+6=0平行.
解: (3) 设经过二直线交点的直线方程为:
所以直线的方程为:
∵直线l和直线2x-y+6=0平行
求过两直线x-2y+4=0和x+y-2=0的交点,且满足下列条件的直线l的方程.
(1)过点(2,1);
(2)和直线3x-4y+5=0垂直;
(3)和直线2x-y+6=0平行.
课堂小结
解直线,的方程组成的方程组
(1)若方程组有唯一解,则与相交此解就是交点的坐标;
(2)若方程组无解,则﹔
(3)若方程组中的两个方程可化成同一个方程,则与重合.
判断两条直线的位置关系:
(1)求解
(2)斜率
(3)图像
复习回顾
点斜式
斜截式
两点式
截距式
一般式
第二章 直线和圆的方程
2.3 直线的交点坐标与距离公式
课时1 两条直线的交点坐标
1.会用解方程组的方法求两条相交直线的交点坐标.(数学运算)
2.会根据方程解的个数判定两条直线的位置关系.(直观想象)
几何元素及关系 代数表示
点A
直线l
点A在直线l上
直线l1与l2的交点是A
A的坐标满足方程
A的坐标是方程组
一、两条直线的交点
做一做:
讨论下列二元一次方程组解的情况:
无数组解
无解
重合
平行
一组解
相交
两条直线的交点坐标是下列方程组的解
(1)联立
(2)求解
(3)得交点
(1)若方程组有且只有一个解,
(2)若方程组无解,
(3)若方程组有无数解,
则l1// l2;
则l1与l2相交;
则l1与l2重合.
两条直线的交点的分类:
*结论:
求下列两条直线的交点:
l1:3x+4y-2=0; l2:2x+y+2=0.
解: 解方程组
∴l1与l2的交点是M(- 2,2)
x
y
M
-2
2
0
l1
l2
例1
例2:判定下列各对直线的位置关系,若相交,则求交点的坐标
(1)
解:解方程组
得
所以直线l1与l2相交,交点是
例题分析:例 2(1)
另一方面,
(2)
另一方面,
无解
所以 l1 // l2
所以直线 l1 与 l2 无公共点,l1 // l2
解:解方程组
例题分析:例 2(2)
(3)
∴直线l1与l2重合
解: ∵
∴直线l1与l2的方程可化为同一个方程
∴直线l1与l2的方程表示同一条直线
例题分析: 例 2(3)
用斜率判断和通过解方程组判断这两种方法都是通过代数方法研究两条直线的位置关系.用斜率容易判断两条直线平行或相交(或垂直),但无法直接得出相交时两条直线的交点坐标.
还有其他方法吗?
画图!画出直线
新知运用
例1 求过直线
拓展:直线系方程
一般地,具有某种共同属性的一类直线的集合称为直线系,它的方程叫作直线系方程。直线系方程中除含变量x,y以外,还有根据具体条件取不同值的变量,称为参变量,简称参数。由于参数的属性及取法不同,故可得到不同的直线系。根据直线系的属性,常见的直线系有:
(1)共点直线系方程:经过直线l1:,l2: 交点的直线系方程为:
①(,为参变量,且,不同时为0)
②(为待定的系数)
=0时,方程为3x+4y-2=0
x
y
=1时,方程为5x+5y=0
=-1时,方程为x+3y-4=0
O
上式整理为:(3+2λ)x+(4+λ)y+2λ-2=0
几何意义: 此方程表示经过直线3x+4y-2=0与直线2x+y+2=0 交点的直线集合(直线束).
共点直线系方程
(2)平行直线系方程:与直线平行的直线系方程为
(为参变量,且
(3)垂直直线系方程:与直线垂直的直线系方程为
(为参变量
例1用直线系方程解
例1 求过直线
所以直线的方程为:
解: (1) 设经过二直线交点的直线方程为:
巩固练习
求过两直线x-2y+4=0和x+y-2=0的交点,且满足下列条件的直线l的方程.
(1)过点(2,1);
(2)和直线3x-4y+5=0垂直;
(3)和直线2x-y+6=0平行.
∵直线l过点(2,1)
解: (2) 设经过二直线交点的直线方程为:
所以直线的方程为:
∵直线l和直线3x-4y+5=0垂直
求过两直线x-2y+4=0和x+y-2=0的交点,且满足下列条件的直线l的方程.
(1)过点(2,1);
(2)和直线3x-4y+5=0垂直;
(3)和直线2x-y+6=0平行.
解: (3) 设经过二直线交点的直线方程为:
所以直线的方程为:
∵直线l和直线2x-y+6=0平行
求过两直线x-2y+4=0和x+y-2=0的交点,且满足下列条件的直线l的方程.
(1)过点(2,1);
(2)和直线3x-4y+5=0垂直;
(3)和直线2x-y+6=0平行.
课堂小结
解直线,的方程组成的方程组
(1)若方程组有唯一解,则与相交此解就是交点的坐标;
(2)若方程组无解,则﹔
(3)若方程组中的两个方程可化成同一个方程,则与重合.
判断两条直线的位置关系:
(1)求解
(2)斜率
(3)图像
