2.2 基本不等式第2课时 基本不等式的应用人教A版(2019)必修 第一册第二章 一元二次函数、方程和不等式(习题课共31张PPT)
文档属性
| 名称 | 2.2 基本不等式第2课时 基本不等式的应用人教A版(2019)必修 第一册第二章 一元二次函数、方程和不等式(习题课共31张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-09 00:28:22 | ||
图片预览










文档简介
(共31张PPT)
第2课时 基本不等式的应用(习题课)
知识探究·素养启迪
课堂探究·素养培育
知识探究·素养启迪
小试身手
AC
3.若实数x,y满足xy=1,则x2+2y2的最小值为 .
4.长为2L的铁丝,围成一个矩形,该矩形的最大面积为 .
课堂探究·素养培育
探究点一
利用基本不等式求解实际问题中的最值
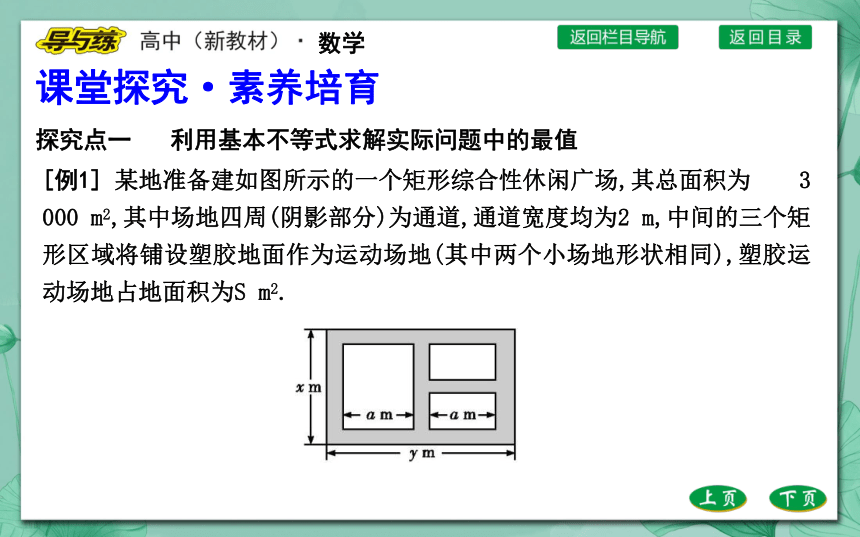
[例1] 某地准备建如图所示的一个矩形综合性休闲广场,其总面积为 3 000 m2,其中场地四周(阴影部分)为通道,通道宽度均为2 m,中间的三个矩形区域将铺设塑胶地面作为运动场地(其中两个小场地形状相同),塑胶运动场地占地面积为S m2.
(1)分别写出用x表示y和S的关系式;
(2)怎样设计能使S取得最大值,最大值为多少
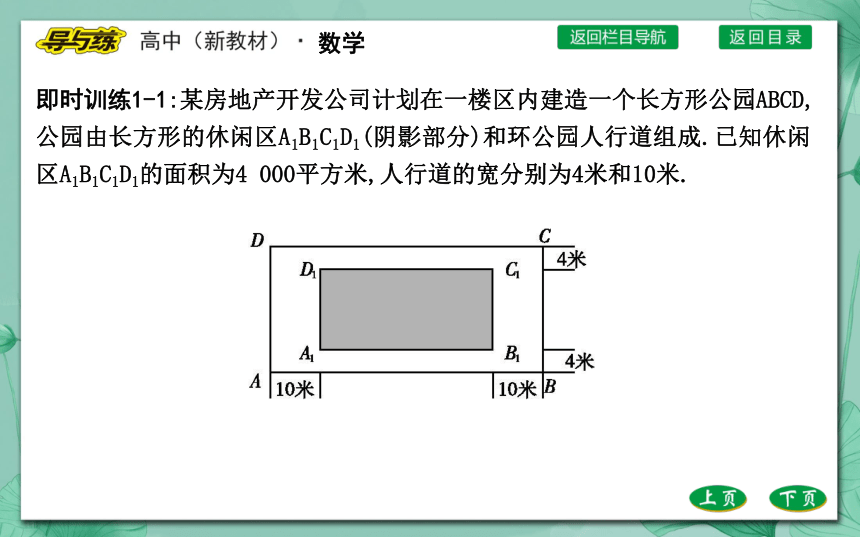
即时训练1-1:某房地产开发公司计划在一楼区内建造一个长方形公园ABCD,公园由长方形的休闲区A1B1C1D1(阴影部分)和环公园人行道组成.已知休闲区A1B1C1D1的面积为4 000平方米,人行道的宽分别为4米和10米.
(1)若设休闲区的长A1B1=x米,求公园ABCD所占面积S关于x的函数S(x)的解析式;
(2)要使公园所占面积最小,休闲区A1B1C1D1的长和宽该如何设计
探究点二
利用基本不等式求条件最值
(A)xy有最大值64
(B)xy有最小值64
(C)x+y有最小值18
(D)x+y有最小值16
方法总结
常数代换法适用于求解条件最值问题,应用此种方法求解最值的基本步骤为
(1)根据已知条件或其变形确定定值(常数);
(2)把确定的定值(常数)变形为1;
(3)把“1”的表达式与所求最值的表达式相乘或相除,进而构造和或积的形式;
(4)利用基本不等式求解最值.
探究点三
利用基本不等式求解含参数的恒成立问题
[例3] 若x>0时,x2-(k+1)x+2>0恒成立,求k的取值范围.
即时训练3-1:若x>0时,不等式x2+mx+4≥0恒成立,求实数m的取值范围.
方法总结
含参数的不等式恒成立问题,若能分离参数,常分离参数后求解.一般地,若a≥f(x)恒成立,则a≥f(x)的最大值(其中f(x)是关于变量x的关系式), a≤f(x)恒成立,则a≤f(x)的最小值.若a≥f(x)有解,则a≥f(x)的最小 值,a≤f(x)有解,则a≤f(x)的最大值.
备用例题
[例1] 设矩形ABCD(其中AB>BC)的周长为24,如图所示,把它沿对角线AC对折后,AB交DC于点P.设AB=x,求△ADP的最大面积.
课堂达标
答案:3
4.若x<0且不等式x2-ax+1≥0恒成立,则a的最小值是 .
答案:-2
第2课时 基本不等式的应用(习题课)
知识探究·素养启迪
课堂探究·素养培育
知识探究·素养启迪
小试身手
AC
3.若实数x,y满足xy=1,则x2+2y2的最小值为 .
4.长为2L的铁丝,围成一个矩形,该矩形的最大面积为 .
课堂探究·素养培育
探究点一
利用基本不等式求解实际问题中的最值
[例1] 某地准备建如图所示的一个矩形综合性休闲广场,其总面积为 3 000 m2,其中场地四周(阴影部分)为通道,通道宽度均为2 m,中间的三个矩形区域将铺设塑胶地面作为运动场地(其中两个小场地形状相同),塑胶运动场地占地面积为S m2.
(1)分别写出用x表示y和S的关系式;
(2)怎样设计能使S取得最大值,最大值为多少
即时训练1-1:某房地产开发公司计划在一楼区内建造一个长方形公园ABCD,公园由长方形的休闲区A1B1C1D1(阴影部分)和环公园人行道组成.已知休闲区A1B1C1D1的面积为4 000平方米,人行道的宽分别为4米和10米.
(1)若设休闲区的长A1B1=x米,求公园ABCD所占面积S关于x的函数S(x)的解析式;
(2)要使公园所占面积最小,休闲区A1B1C1D1的长和宽该如何设计
探究点二
利用基本不等式求条件最值
(A)xy有最大值64
(B)xy有最小值64
(C)x+y有最小值18
(D)x+y有最小值16
方法总结
常数代换法适用于求解条件最值问题,应用此种方法求解最值的基本步骤为
(1)根据已知条件或其变形确定定值(常数);
(2)把确定的定值(常数)变形为1;
(3)把“1”的表达式与所求最值的表达式相乘或相除,进而构造和或积的形式;
(4)利用基本不等式求解最值.
探究点三
利用基本不等式求解含参数的恒成立问题
[例3] 若x>0时,x2-(k+1)x+2>0恒成立,求k的取值范围.
即时训练3-1:若x>0时,不等式x2+mx+4≥0恒成立,求实数m的取值范围.
方法总结
含参数的不等式恒成立问题,若能分离参数,常分离参数后求解.一般地,若a≥f(x)恒成立,则a≥f(x)的最大值(其中f(x)是关于变量x的关系式), a≤f(x)恒成立,则a≤f(x)的最小值.若a≥f(x)有解,则a≥f(x)的最小 值,a≤f(x)有解,则a≤f(x)的最大值.
备用例题
[例1] 设矩形ABCD(其中AB>BC)的周长为24,如图所示,把它沿对角线AC对折后,AB交DC于点P.设AB=x,求△ADP的最大面积.
课堂达标
答案:3
4.若x<0且不等式x2-ax+1≥0恒成立,则a的最小值是 .
答案:-2
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
