5.1.2相交线,新人教版[下学期]
文档属性
| 名称 | 5.1.2相交线,新人教版[下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 295.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-02-20 00:00:00 | ||
图片预览




文档简介
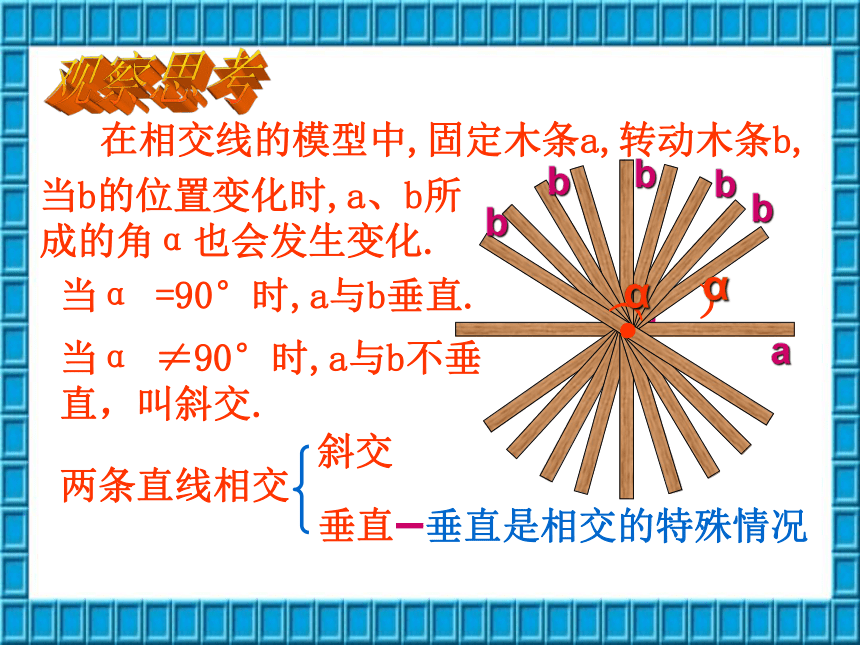
课件10张PPT。5.1 相交线孝感市文昌中学 程世富(5.1.2 垂线)在相交线的模型中,固定木条a,转动木条b,当α =90°时,a与b垂直.当b的位置变化时,a、b所成的角α也会发生变化.当α ≠90°时,a与b不垂直,叫斜交.两条直线相交斜交垂直垂直是相交的特殊情况观察思考)α abbbbb)α 1.垂直定义:当两条直线相交所成的四个角中,有一个角是直角时,这两条直线互相垂直,其中一条直线叫另一条直线的垂线,它们的交点叫垂足。例如、如图,a、b互相垂直,O叫垂足.a叫b的垂线,b也叫a的垂线。一、垂直的定义从垂直的定义可知,
判断两条直线互相垂直的关键:
只要找到两条直线相交时四个交角中一个角是直角。1.垂直定义:当两条直线相交所成的四个角中,有一个角是直角时,这两条直线互相垂直,其中一条直线叫另一条直线的垂线,它们的交点叫垂足。ba用“⊥”和直线字母表示垂直Oα 2.垂直的表示:例如、如图,a、b互相垂直, 垂足为O,则记为:a⊥b或b⊥a, 若要强调垂足,则记为:a⊥b, 垂足为O. 日常生活中,两条直线互相垂直的情形很常见,说出图5.1-6中的一些互相垂直的线条.你能再举出其他例子吗?ABCDO书写形式: 如图,当直线AB与CD相交于O点,∠AOD=90°时,AB⊥CD,垂足为O。∵∠AOD=90°(已知)
∴AB⊥CD(垂直的定义)书写形式: 反之,若直线AB与CD垂直,垂足为O,那么,∠AOD=90°。3.垂直的书写形式:∵ AB⊥CD (已知)
∴ ∠AOD=90° (垂直的定义)应用垂直的定义:∠AOC=∠BOC=∠BOD=90°例1 如图,直线AB、CD相交于点O,OE⊥AB,∠1=55°,求∠EOD的度数.ACEBDO1∴ ∠EOB=90°(垂直的定义) ∴ ∠ EOD= ∠ EOB+ ∠ BOD
=90 °+55 °=145 °(解:∵ AB⊥OE (已知)∵ ∠BOD= ∠1=55°
(对顶角相等)二、例题例2 如图,直线AB、CD相交于点O,OE⊥AB于O,OB平分∠ DOF,∠DOE=50°,求∠AOC、 ∠ EOF、 ∠ COF的度数.ACEBDO∴ ∠EOB=90°(垂直的定义) ∴ ∠COF=∠COD-∠DOF=180°-80°=100°
(邻补角定义)解:∵ AB⊥OE (已知)∴ ∠AOC= ∠DOB=40°(对顶角相等)F∵ ∠DOE= 50° (已知)∴ ∠DOB=40°(互余的定义)又∵OB平分∠DOF∴ ∠BOF= ∠DOB=40°(角平分线定义) ∴ ∠EOF= ∠EOB+ ∠BOF=90°+40°=130°作业: P9/3补充: 如图,直线AB、CD相交于点O,OE⊥AB,∠1=125°,
求∠COE的度数.ACEBDO1)再见
判断两条直线互相垂直的关键:
只要找到两条直线相交时四个交角中一个角是直角。1.垂直定义:当两条直线相交所成的四个角中,有一个角是直角时,这两条直线互相垂直,其中一条直线叫另一条直线的垂线,它们的交点叫垂足。ba用“⊥”和直线字母表示垂直Oα 2.垂直的表示:例如、如图,a、b互相垂直, 垂足为O,则记为:a⊥b或b⊥a, 若要强调垂足,则记为:a⊥b, 垂足为O. 日常生活中,两条直线互相垂直的情形很常见,说出图5.1-6中的一些互相垂直的线条.你能再举出其他例子吗?ABCDO书写形式: 如图,当直线AB与CD相交于O点,∠AOD=90°时,AB⊥CD,垂足为O。∵∠AOD=90°(已知)
∴AB⊥CD(垂直的定义)书写形式: 反之,若直线AB与CD垂直,垂足为O,那么,∠AOD=90°。3.垂直的书写形式:∵ AB⊥CD (已知)
∴ ∠AOD=90° (垂直的定义)应用垂直的定义:∠AOC=∠BOC=∠BOD=90°例1 如图,直线AB、CD相交于点O,OE⊥AB,∠1=55°,求∠EOD的度数.ACEBDO1∴ ∠EOB=90°(垂直的定义) ∴ ∠ EOD= ∠ EOB+ ∠ BOD
=90 °+55 °=145 °(解:∵ AB⊥OE (已知)∵ ∠BOD= ∠1=55°
(对顶角相等)二、例题例2 如图,直线AB、CD相交于点O,OE⊥AB于O,OB平分∠ DOF,∠DOE=50°,求∠AOC、 ∠ EOF、 ∠ COF的度数.ACEBDO∴ ∠EOB=90°(垂直的定义) ∴ ∠COF=∠COD-∠DOF=180°-80°=100°
(邻补角定义)解:∵ AB⊥OE (已知)∴ ∠AOC= ∠DOB=40°(对顶角相等)F∵ ∠DOE= 50° (已知)∴ ∠DOB=40°(互余的定义)又∵OB平分∠DOF∴ ∠BOF= ∠DOB=40°(角平分线定义) ∴ ∠EOF= ∠EOB+ ∠BOF=90°+40°=130°作业: P9/3补充: 如图,直线AB、CD相交于点O,OE⊥AB,∠1=125°,
求∠COE的度数.ACEBDO1)再见
