第六章 6.4平面向量的应用-用向量法研究三角形的性质 课件(共22张PPT)
文档属性
| 名称 | 第六章 6.4平面向量的应用-用向量法研究三角形的性质 课件(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 712.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-08 22:06:19 | ||
图片预览


文档简介
(共22张PPT)
用向量法研究
三角形的性质
情境引入
SITUATIONAL INTRODUCTION
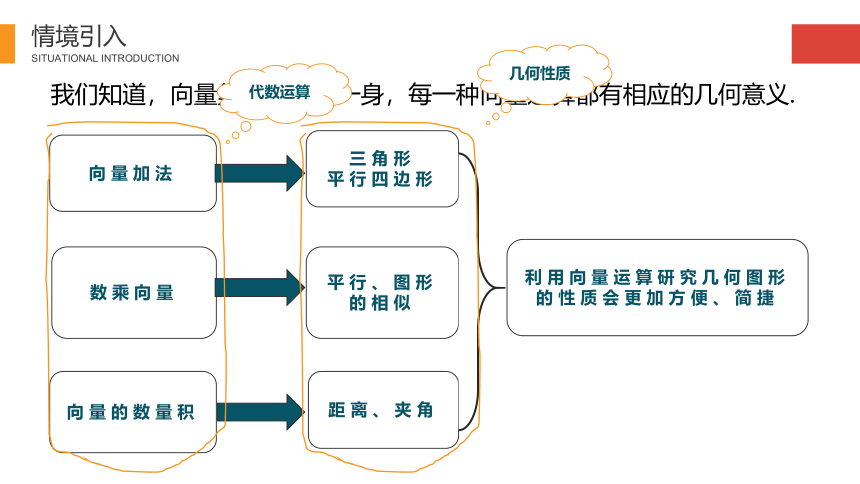
我们知道,向量集数与形于一身,每一种向量运算都有相应的几何意义.
向量加法
三角形
平行四边形
数乘向量
平行、图形的相似
向量的数量积
距离、夹角
利用向量运算研究几何图形的性质会更加方便、简捷
代数运算
几何性质
情境引入
SITUATIONAL INTRODUCTION
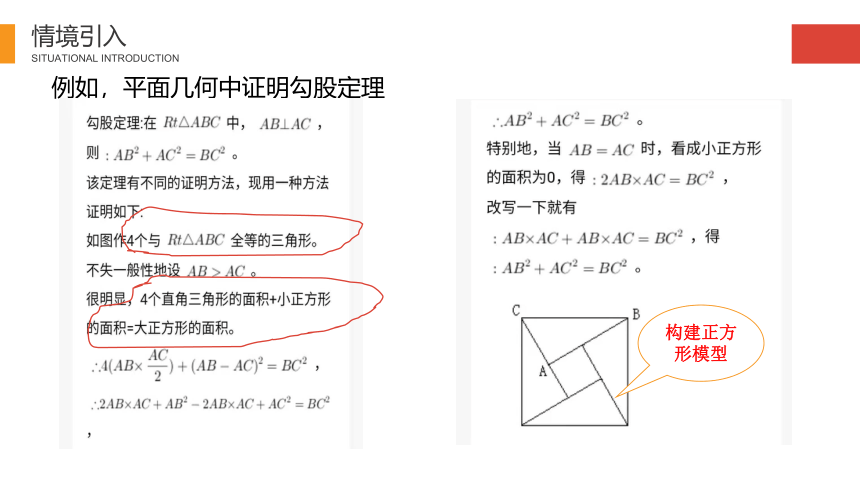
例如,平面几何中证明勾股定理
构建正方形模型
情境引入
SITUATIONAL INTRODUCTION
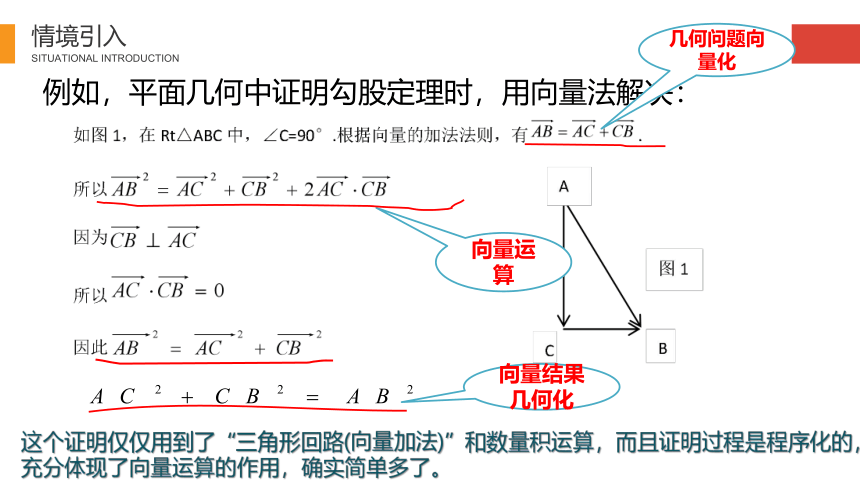
例如,平面几何中证明勾股定理时,用向量法解决:
这个证明仅仅用到了“三角形回路(向量加法)”和数量积运算,而且证明过程是程序化的,充分体现了向量运算的作用,确实简单多了。
几何问题向量化
向量运算
向量结果几何化
问题解决
THE PROBLEM IS RESOLVED
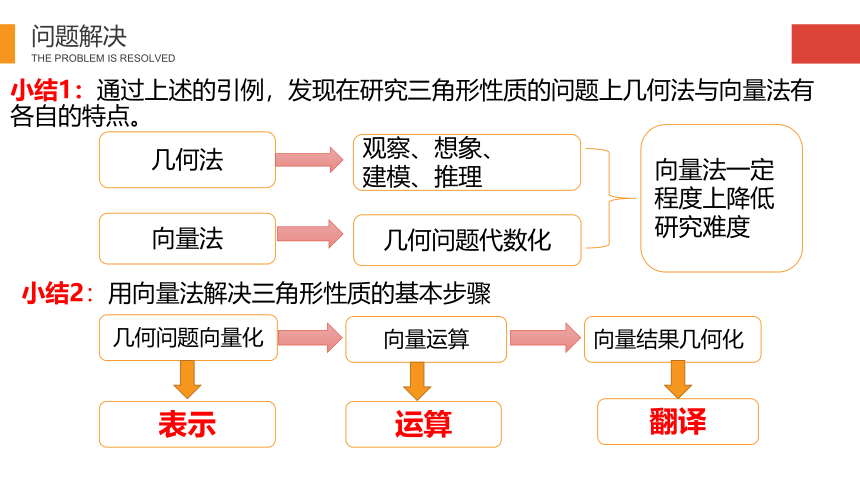
小结1:通过上述的引例,发现在研究三角形性质的问题上几何法与向量法有各自的特点。
小结2:用向量法解决三角形性质的基本步骤
几何法
观察、想象、
建模、推理
向量法
几何问题代数化
向量法一定程度上降低研究难度
几何问题向量化
翻译
运算
表示
向量结果几何化
向量运算
探究什么
THE PROBLEM IS RESOLVED
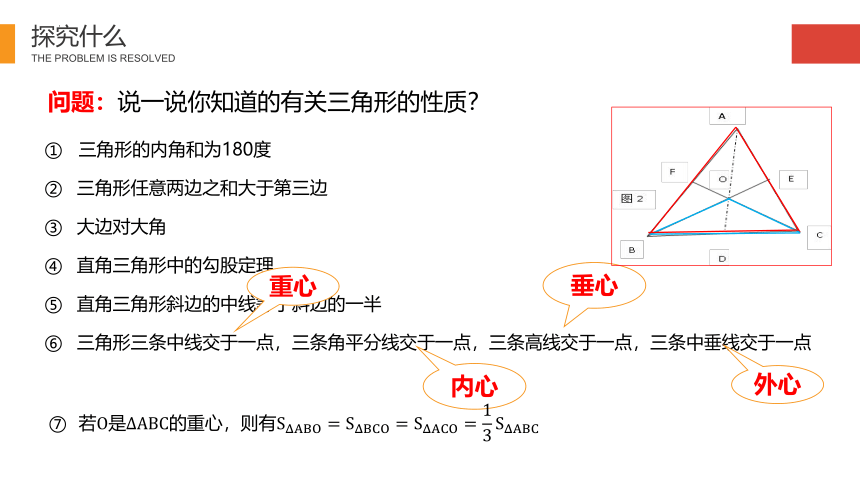
问题:说一说你知道的有关三角形的性质?
三角形的内角和为180度
三角形任意两边之和大于第三边
大边对大角
直角三角形中的勾股定理
直角三角形斜边的中线等于斜边的一半
三角形三条中线交于一点,三条角平分线交于一点,三条高线交于一点,三条中垂线交于一点
重心
内心
垂心
外心
探究活动
THE PROBLEM IS RESOLVED
向量加法
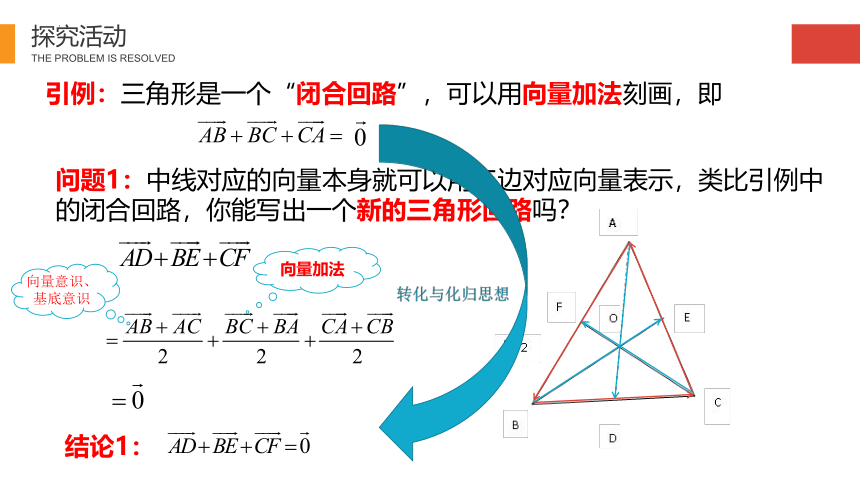
引例:三角形是一个“闭合回路”,可以用向量加法刻画,即
问题1:中线对应的向量本身就可以用三边对应向量表示,类比引例中的闭合回路,你能写出一个新的三角形回路吗?
结论1:
转化与化归思想
向量意识、基底意识
探究活动
THE PROBLEM IS RESOLVED
向量数乘运算
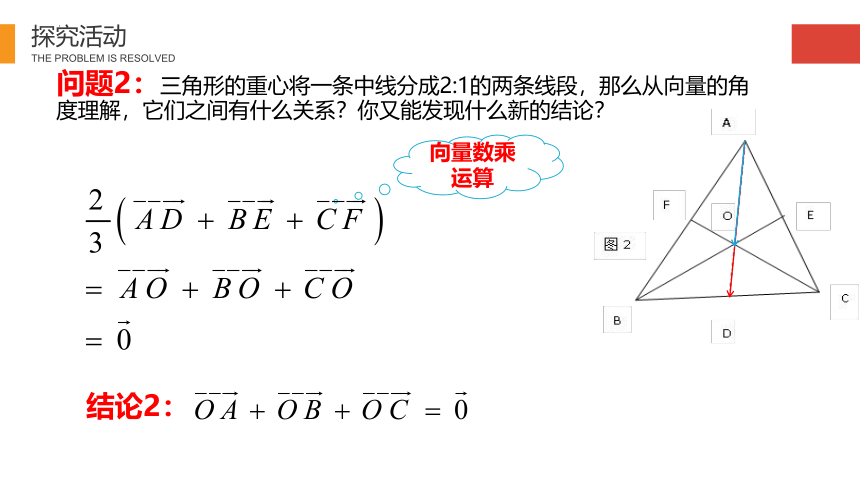
问题2:三角形的重心将一条中线分成2:1的两条线段,那么从向量的角度理解,它们之间有什么关系?你又能发现什么新的结论?
结论2:
探究活动
THE PROBLEM IS RESOLVED
问题3:与向量加法有密切联系的是向量的减法运算,引入平面上任意一点 ,结合向量减法运算,你能将 作出怎样的转化?
结论3:
向量减法
探究活动
THE PROBLEM IS RESOLVED
问题4:数量积是向量运算中非常重要的一种,本节课的主题是“用向量法研究三角形中线和重心的性质”,那么你会将中线与谁进行数量积运算?你能发现一个有关中线的数量积运算结果吗?
我们发现:
数量积运算
结论4:
向量意识、基底意识
向量法的本质:
以数代形
探究活动
THE PROBLEM IS RESOLVED
问题5:前面我们探究了很多关于中线和重心 的性质,那么请大家继续,大胆猜测点 还是哪个三角形的重心。
我们猜测:
结论5:
比如:
总结归纳
SITUATIONAL INTRODUCTION
用向量法研究三角形重心性质
三角形闭合回路
向量
加法
数乘运算
向量减法
数量积运算
回归几何
总结归纳
SITUATIONAL INTRODUCTION
用向量法解决三角形性质
1、用向量法解决三角形性质的本质:
以数代形
2、数学意识方面:
向量意识
基底意识
运算意识
数形结合意识
3、数学思想方法方面:
数形结合思想
转化与化归思想
研究报告
RESEARCH REPORT
用向量法研究三角形的性质
1.本课题组的的成员姓名:
2.发现的数学结论及发现过程概述
三角形是一个“闭合回路”,可以用向量加法刻画,即,而中线对应的向量本身就可以用三边对应向量表示,所以指引我们去探究新的有关重心的性质
3.证明思路及其形成过程描述
思路:将中线向量用三边对应向量表示,并结合向量加法、数乘、数量积等运算得出不同的结论
4.结论的证明或否定
选题
开题
做题
结题
总结归纳:
SITUATIONAL INTRODUCTION
这为我们以后的数学探究之路指引了方向
探究课
开 题
选 题
探究之法(向量法)
探究之道
做 题
解 题
翻 译
表 示
运 算
应用解题
SITUATIONAL INTRODUCTION
表示
运算
翻译
与三角形重心有关的性质:
NATURE RELATED TO THE CENTER OF GRAVITY OF THE TRIANGLE
与三角形重心有关的性质:
NATURE RELATED TO THE CENTER OF GRAVITY OF THE TRIANGLE
课后作业:
AFTER-SCHOOL HOMEWORK
用向量法研究三角形的其它性质,每位学生给出三角形垂心、内心、外心的向量表示及结论
研究报告
选
题
从以下几个课题中选择一个进行研究:
(1)探究2:《三角形角平分线的交点即三角形的内心》
(2)探究3:《三角形高的交点即三角形的垂心》
(3)探究4:《三角形边长的中垂线的交点即三角形的外心》
建议步骤
1、学生分为6组,确定一人为组长;
2、小组集体讨论探究方案,确定研究思路;
3、小组成员各自开展独立研究,并以专题作业的形式撰写研究报告;
4、小组内进行交流讨论,完善研究成果,并形成一份小组研究报告;全班进行成
果交流、评价。
研究报告:
RESEARCH REPORT
用向量法研究三角形的性质
1.本课题组的的成员姓名
2.发现的数学结论及发现过程概述
3.证明思路及其形成过程描述
4.结论的证明或否定
课堂练习:
感谢聆听,批评指导
用向量法研究
三角形的性质
情境引入
SITUATIONAL INTRODUCTION
我们知道,向量集数与形于一身,每一种向量运算都有相应的几何意义.
向量加法
三角形
平行四边形
数乘向量
平行、图形的相似
向量的数量积
距离、夹角
利用向量运算研究几何图形的性质会更加方便、简捷
代数运算
几何性质
情境引入
SITUATIONAL INTRODUCTION
例如,平面几何中证明勾股定理
构建正方形模型
情境引入
SITUATIONAL INTRODUCTION
例如,平面几何中证明勾股定理时,用向量法解决:
这个证明仅仅用到了“三角形回路(向量加法)”和数量积运算,而且证明过程是程序化的,充分体现了向量运算的作用,确实简单多了。
几何问题向量化
向量运算
向量结果几何化
问题解决
THE PROBLEM IS RESOLVED
小结1:通过上述的引例,发现在研究三角形性质的问题上几何法与向量法有各自的特点。
小结2:用向量法解决三角形性质的基本步骤
几何法
观察、想象、
建模、推理
向量法
几何问题代数化
向量法一定程度上降低研究难度
几何问题向量化
翻译
运算
表示
向量结果几何化
向量运算
探究什么
THE PROBLEM IS RESOLVED
问题:说一说你知道的有关三角形的性质?
三角形的内角和为180度
三角形任意两边之和大于第三边
大边对大角
直角三角形中的勾股定理
直角三角形斜边的中线等于斜边的一半
三角形三条中线交于一点,三条角平分线交于一点,三条高线交于一点,三条中垂线交于一点
重心
内心
垂心
外心
探究活动
THE PROBLEM IS RESOLVED
向量加法
引例:三角形是一个“闭合回路”,可以用向量加法刻画,即
问题1:中线对应的向量本身就可以用三边对应向量表示,类比引例中的闭合回路,你能写出一个新的三角形回路吗?
结论1:
转化与化归思想
向量意识、基底意识
探究活动
THE PROBLEM IS RESOLVED
向量数乘运算
问题2:三角形的重心将一条中线分成2:1的两条线段,那么从向量的角度理解,它们之间有什么关系?你又能发现什么新的结论?
结论2:
探究活动
THE PROBLEM IS RESOLVED
问题3:与向量加法有密切联系的是向量的减法运算,引入平面上任意一点 ,结合向量减法运算,你能将 作出怎样的转化?
结论3:
向量减法
探究活动
THE PROBLEM IS RESOLVED
问题4:数量积是向量运算中非常重要的一种,本节课的主题是“用向量法研究三角形中线和重心的性质”,那么你会将中线与谁进行数量积运算?你能发现一个有关中线的数量积运算结果吗?
我们发现:
数量积运算
结论4:
向量意识、基底意识
向量法的本质:
以数代形
探究活动
THE PROBLEM IS RESOLVED
问题5:前面我们探究了很多关于中线和重心 的性质,那么请大家继续,大胆猜测点 还是哪个三角形的重心。
我们猜测:
结论5:
比如:
总结归纳
SITUATIONAL INTRODUCTION
用向量法研究三角形重心性质
三角形闭合回路
向量
加法
数乘运算
向量减法
数量积运算
回归几何
总结归纳
SITUATIONAL INTRODUCTION
用向量法解决三角形性质
1、用向量法解决三角形性质的本质:
以数代形
2、数学意识方面:
向量意识
基底意识
运算意识
数形结合意识
3、数学思想方法方面:
数形结合思想
转化与化归思想
研究报告
RESEARCH REPORT
用向量法研究三角形的性质
1.本课题组的的成员姓名:
2.发现的数学结论及发现过程概述
三角形是一个“闭合回路”,可以用向量加法刻画,即,而中线对应的向量本身就可以用三边对应向量表示,所以指引我们去探究新的有关重心的性质
3.证明思路及其形成过程描述
思路:将中线向量用三边对应向量表示,并结合向量加法、数乘、数量积等运算得出不同的结论
4.结论的证明或否定
选题
开题
做题
结题
总结归纳:
SITUATIONAL INTRODUCTION
这为我们以后的数学探究之路指引了方向
探究课
开 题
选 题
探究之法(向量法)
探究之道
做 题
解 题
翻 译
表 示
运 算
应用解题
SITUATIONAL INTRODUCTION
表示
运算
翻译
与三角形重心有关的性质:
NATURE RELATED TO THE CENTER OF GRAVITY OF THE TRIANGLE
与三角形重心有关的性质:
NATURE RELATED TO THE CENTER OF GRAVITY OF THE TRIANGLE
课后作业:
AFTER-SCHOOL HOMEWORK
用向量法研究三角形的其它性质,每位学生给出三角形垂心、内心、外心的向量表示及结论
研究报告
选
题
从以下几个课题中选择一个进行研究:
(1)探究2:《三角形角平分线的交点即三角形的内心》
(2)探究3:《三角形高的交点即三角形的垂心》
(3)探究4:《三角形边长的中垂线的交点即三角形的外心》
建议步骤
1、学生分为6组,确定一人为组长;
2、小组集体讨论探究方案,确定研究思路;
3、小组成员各自开展独立研究,并以专题作业的形式撰写研究报告;
4、小组内进行交流讨论,完善研究成果,并形成一份小组研究报告;全班进行成
果交流、评价。
研究报告:
RESEARCH REPORT
用向量法研究三角形的性质
1.本课题组的的成员姓名
2.发现的数学结论及发现过程概述
3.证明思路及其形成过程描述
4.结论的证明或否定
课堂练习:
感谢聆听,批评指导
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
