平行线复习课[下学期]
图片预览


文档简介
平行线(复习课)教案
目的要求:
1、复习巩固平行线的判定和性质,能应用判定和性质进行简单的推理或计算。
2、使学生进一步学会识图,能将复杂图形分解为基本图形,学会图形、符号语言、几何语言的转化。
3、通过复习使学生了解分析问题的方法(分析法、综合法),初步领会化繁为简、化未知为已知的化归思想。
教学重点:
使学生掌握平行线的判定和性质,并能用它们进行简单的推理或计算,初步掌握分析问题和解决问题的方法。
教学难点:
使学生将知识条理化、系统化,能正确地运用。
教学过程:
一、复习引入:(2分钟)
老师:在同一平面上,两条直线的位置关系有几种?学生:有两种,或者相交,或者平行。这一节课我们就来复行线的判定与性质”。
(板书课题:平行线的判定与性质)
二、基础回顾:(5分钟)
1、定义:
教师:什么叫做平行线?
学生:在同一平面上,不相交的两直线叫平行线。
教师:答得很对。
2、如何判定两直线平行?
如果两直线平行,你可以得到什么性质?
填表:
平行线的判定 平行线的性质
1、 ,两直线平行。2、 ,两直线平行。3、 ,两直线平行。4、 的两直线平行。 1、两直线平行, 。2、两直线平行, 。3、两直线平行, 。
3、平行线的“判定”和“性质”之间有什么关系吗?
4、练习:
判断:
(1)两条直线被第三条直线所截,同位角相等( )
(2)同旁内角互补 ( )
(3)如果a⊥b且a⊥c,那么直线b∥c ( )
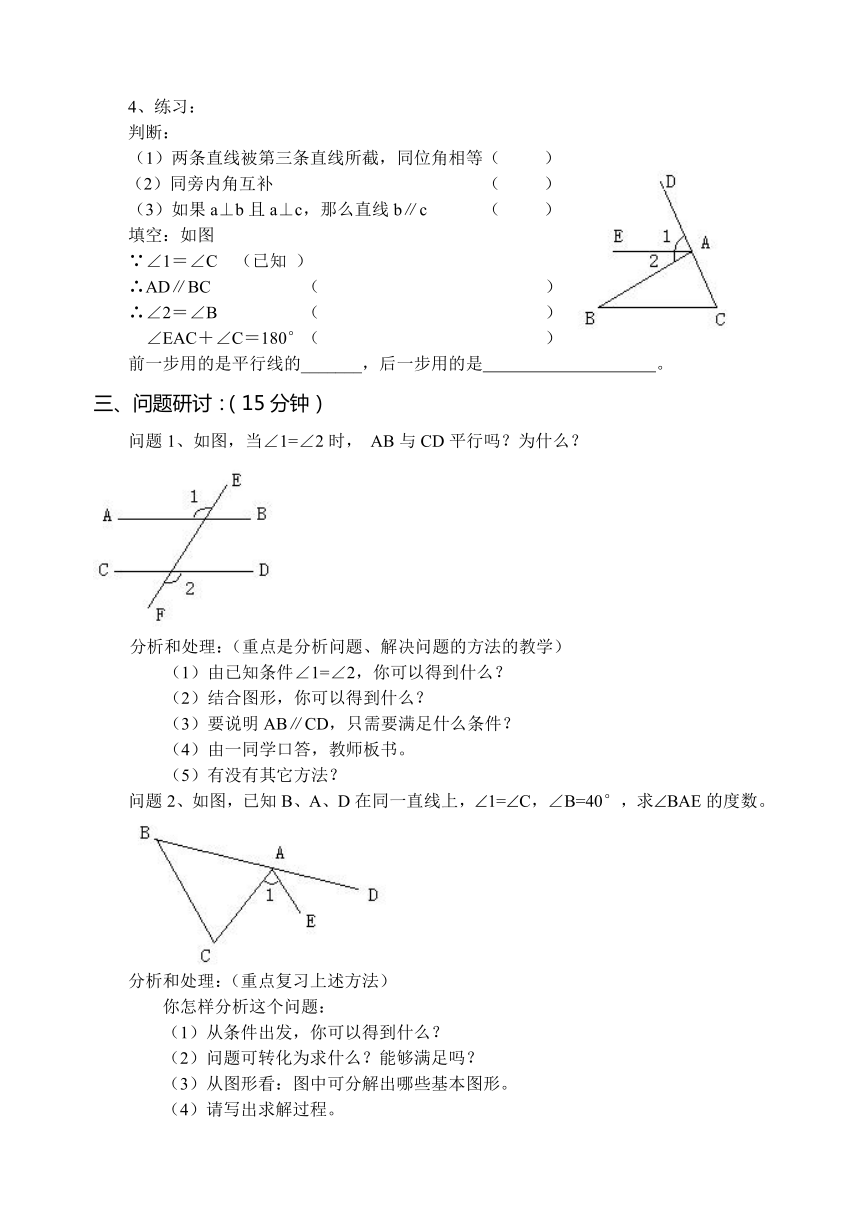
填空:如图
∵∠1=∠C (已知 )
∴AD∥BC ( )
∴∠2=∠B ( )
∠EAC+∠C=180°( )
前一步用的是平行线的_______,后一步用的是 。
三、问题研讨:(15分钟)
问题1、如图,当∠1=∠2时, AB与CD平行吗?为什么?
分析和处理:(重点是分析问题、解决问题的方法的教学)
(1)由已知条件∠1=∠2,你可以得到什么?
(2)结合图形,你可以得到什么?
(3)要说明AB∥CD,只需要满足什么条件?
(4)由一同学口答,教师板书。
(5)有没有其它方法?
问题2、如图,已知B、A、D在同一直线上,1=C,∠B=40°,求BAE的度数。
分析和处理:(重点复习上述方法)
你怎样分析这个问题:
(1)从条件出发,你可以得到什么?
(2)问题可转化为求什么?能够满足吗?
(3)从图形看:图中可分解出哪些基本图形。
(4)请写出求解过程。
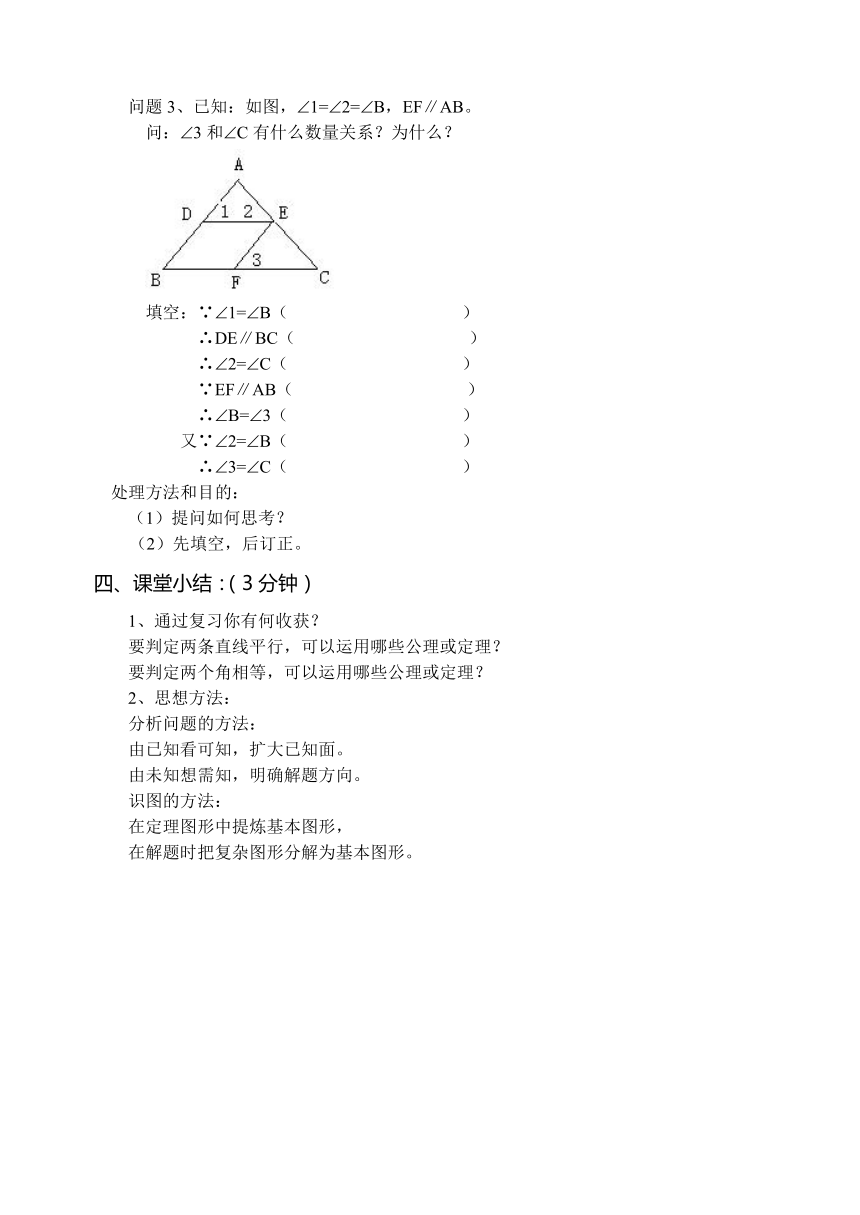
问题3、已知:如图,1=2=B,EF∥AB。
问:3和C有什么数量关系?为什么?
填空:∵1=B( )
∴DE∥BC( )
∴2=C( )
∵EF∥AB( )
∴B=3( )
又∵2=B( )
∴3=C( )
处理方法和目的:
(1)提问如何思考?
(2)先填空,后订正。
四、课堂小结:(3分钟)
1、通过复习你有何收获?
要判定两条直线平行,可以运用哪些公理或定理?
要判定两个角相等,可以运用哪些公理或定理?
2、思想方法:
分析问题的方法:
由已知看可知,扩大已知面。
由未知想需知,明确解题方向。
识图的方法:
在定理图形中提炼基本图形,
在解题时把复杂图形分解为基本图形。
五、课堂练习:(10分钟+3分钟)
1、填空:
(1)∵∠1=∠B(已知)
∴ ∥ ( )
(2)∵∠2=∠3(已知)
∴ ∥ ( )
∴∠B= ( )
2、如图,已知CD∥AB,EF∥AB,求∠A+∠AEC+∠C的度数。
∵CD∥AB (已知)
∴∠1+∠A=180° ( )
∵CD∥AB,EF∥AB ( )
∴ ∥ ( )
∴∠2+∠C=180° ( )
∴∠1+∠A+∠2+∠C=360°(等式的性质)
即∠A+∠AEC+∠C=360°。
3、如图,已知AB∥CD,∠A+∠B=180°,∠A=∠D吗?为什么?
六、课外作业:(2分钟)
1、∵∠3+∠4=180°(已知)
∴ ∥ ( )
∴∠1= ( )
2、如图,
∵AB∥CD (已知)
∴ = ( )
∵∠1=∠2 ( )
∴ ∥ ( )
∴∠DAB+∠ABC=180°( )
3、如图,已知∠1=∠2=∠3=35°,求∠AED的度数。
分析:
(1)由∠1=∠2=∠3=35°,你能得到 。
(2)分析图形,你能得到什么?
(3)看结论,你能转化为什么问题?
(4)请写出解题过程。
解:
4、如图,已知∠1=∠2,则∠2=∠3吗?为什么?
学习材料:
1、填表:
平行线的判定 平行线的性质
1、 ,两直线平行。2、 ,两直线平行。3、 ,两直线平行。4、 的两直线平行。 1、两直线平行, 。2、两直线平行, 。3、两直线平行, 。
2、练习:
判断:
(1)两条直线被第三条直线所截,同位角相等( )
(2)同旁内角互补 ( )
(3)如果a⊥b且a⊥c,那么直线b∥c ( )
填空:如图
∵∠1=∠C (已知 )
∴AD∥BC ( )
∴∠2=∠B ( )
∠EAC+∠C=180°( )
前一步用的是平行线的_______,后一步用的是 。
3、问题1、如图,当∠1=∠2时, AB与CD平行吗?为什么?
4、问题2、如图,已知B、A、D在同一直线上,1=C,∠B=40°,求BAE的度数。
4、问题3、已知:如图,1=2=B,EF∥AB。
问:3和C有什么数量关系?为什么?
填空:∵1=B( )
∴DE∥BC( )
∴2=C( )
∵EF∥AB( )
∴B=3( )
又∵2=B( )
∴3=C( )
课堂练习:(10分钟+3分钟)
1、填空:
(1)∵∠1=∠B(已知)
∴ ∥ ( )
(2)∵∠2=∠3(已知)
∴ ∥ ( )
∴∠B= ( )
2、如图,已知CD∥AB,EF∥AB,求∠A+∠AEC+∠C的度数。
∵CD∥AB (已知)
∴∠1+∠A=180° ( )
∵CD∥AB,EF∥AB ( )
∴ ∥ ( )
∴∠2+∠C=180° ( )
∴∠1+∠A+∠2+∠C=360°(等式的性质)
即∠A+∠AEC+∠C=360°。
3、如图,已知AB∥CD,∠A+∠B=180°,∠A=∠D吗?为什么?
六、课外作业:(2分钟)
1、∵∠3+∠4=180°(已知)
∴ ∥ ( )
∴∠1= ( )
2、如图,
∵AB∥CD (已知)
∴ = ( )
∵∠1=∠2 ( )
∴ ∥ ( )
∴∠DAB+∠ABC=180°( )
3、如图,已知∠1=∠2=∠3=35°,求∠AED的度数。
分析:
(1)由∠1=∠2=∠3=35°,你能得到 。
(2)分析图形,你能得到什么?
(3)看结论,你能转化为什么问题?
(4)请写出解题过程。
解:
4、如图,已知∠1=∠2,则∠2=∠3吗?为什么?
目的要求:
1、复习巩固平行线的判定和性质,能应用判定和性质进行简单的推理或计算。
2、使学生进一步学会识图,能将复杂图形分解为基本图形,学会图形、符号语言、几何语言的转化。
3、通过复习使学生了解分析问题的方法(分析法、综合法),初步领会化繁为简、化未知为已知的化归思想。
教学重点:
使学生掌握平行线的判定和性质,并能用它们进行简单的推理或计算,初步掌握分析问题和解决问题的方法。
教学难点:
使学生将知识条理化、系统化,能正确地运用。
教学过程:
一、复习引入:(2分钟)
老师:在同一平面上,两条直线的位置关系有几种?学生:有两种,或者相交,或者平行。这一节课我们就来复行线的判定与性质”。
(板书课题:平行线的判定与性质)
二、基础回顾:(5分钟)
1、定义:
教师:什么叫做平行线?
学生:在同一平面上,不相交的两直线叫平行线。
教师:答得很对。
2、如何判定两直线平行?
如果两直线平行,你可以得到什么性质?
填表:
平行线的判定 平行线的性质
1、 ,两直线平行。2、 ,两直线平行。3、 ,两直线平行。4、 的两直线平行。 1、两直线平行, 。2、两直线平行, 。3、两直线平行, 。
3、平行线的“判定”和“性质”之间有什么关系吗?
4、练习:
判断:
(1)两条直线被第三条直线所截,同位角相等( )
(2)同旁内角互补 ( )
(3)如果a⊥b且a⊥c,那么直线b∥c ( )
填空:如图
∵∠1=∠C (已知 )
∴AD∥BC ( )
∴∠2=∠B ( )
∠EAC+∠C=180°( )
前一步用的是平行线的_______,后一步用的是 。
三、问题研讨:(15分钟)
问题1、如图,当∠1=∠2时, AB与CD平行吗?为什么?
分析和处理:(重点是分析问题、解决问题的方法的教学)
(1)由已知条件∠1=∠2,你可以得到什么?
(2)结合图形,你可以得到什么?
(3)要说明AB∥CD,只需要满足什么条件?
(4)由一同学口答,教师板书。
(5)有没有其它方法?
问题2、如图,已知B、A、D在同一直线上,1=C,∠B=40°,求BAE的度数。
分析和处理:(重点复习上述方法)
你怎样分析这个问题:
(1)从条件出发,你可以得到什么?
(2)问题可转化为求什么?能够满足吗?
(3)从图形看:图中可分解出哪些基本图形。
(4)请写出求解过程。
问题3、已知:如图,1=2=B,EF∥AB。
问:3和C有什么数量关系?为什么?
填空:∵1=B( )
∴DE∥BC( )
∴2=C( )
∵EF∥AB( )
∴B=3( )
又∵2=B( )
∴3=C( )
处理方法和目的:
(1)提问如何思考?
(2)先填空,后订正。
四、课堂小结:(3分钟)
1、通过复习你有何收获?
要判定两条直线平行,可以运用哪些公理或定理?
要判定两个角相等,可以运用哪些公理或定理?
2、思想方法:
分析问题的方法:
由已知看可知,扩大已知面。
由未知想需知,明确解题方向。
识图的方法:
在定理图形中提炼基本图形,
在解题时把复杂图形分解为基本图形。
五、课堂练习:(10分钟+3分钟)
1、填空:
(1)∵∠1=∠B(已知)
∴ ∥ ( )
(2)∵∠2=∠3(已知)
∴ ∥ ( )
∴∠B= ( )
2、如图,已知CD∥AB,EF∥AB,求∠A+∠AEC+∠C的度数。
∵CD∥AB (已知)
∴∠1+∠A=180° ( )
∵CD∥AB,EF∥AB ( )
∴ ∥ ( )
∴∠2+∠C=180° ( )
∴∠1+∠A+∠2+∠C=360°(等式的性质)
即∠A+∠AEC+∠C=360°。
3、如图,已知AB∥CD,∠A+∠B=180°,∠A=∠D吗?为什么?
六、课外作业:(2分钟)
1、∵∠3+∠4=180°(已知)
∴ ∥ ( )
∴∠1= ( )
2、如图,
∵AB∥CD (已知)
∴ = ( )
∵∠1=∠2 ( )
∴ ∥ ( )
∴∠DAB+∠ABC=180°( )
3、如图,已知∠1=∠2=∠3=35°,求∠AED的度数。
分析:
(1)由∠1=∠2=∠3=35°,你能得到 。
(2)分析图形,你能得到什么?
(3)看结论,你能转化为什么问题?
(4)请写出解题过程。
解:
4、如图,已知∠1=∠2,则∠2=∠3吗?为什么?
学习材料:
1、填表:
平行线的判定 平行线的性质
1、 ,两直线平行。2、 ,两直线平行。3、 ,两直线平行。4、 的两直线平行。 1、两直线平行, 。2、两直线平行, 。3、两直线平行, 。
2、练习:
判断:
(1)两条直线被第三条直线所截,同位角相等( )
(2)同旁内角互补 ( )
(3)如果a⊥b且a⊥c,那么直线b∥c ( )
填空:如图
∵∠1=∠C (已知 )
∴AD∥BC ( )
∴∠2=∠B ( )
∠EAC+∠C=180°( )
前一步用的是平行线的_______,后一步用的是 。
3、问题1、如图,当∠1=∠2时, AB与CD平行吗?为什么?
4、问题2、如图,已知B、A、D在同一直线上,1=C,∠B=40°,求BAE的度数。
4、问题3、已知:如图,1=2=B,EF∥AB。
问:3和C有什么数量关系?为什么?
填空:∵1=B( )
∴DE∥BC( )
∴2=C( )
∵EF∥AB( )
∴B=3( )
又∵2=B( )
∴3=C( )
课堂练习:(10分钟+3分钟)
1、填空:
(1)∵∠1=∠B(已知)
∴ ∥ ( )
(2)∵∠2=∠3(已知)
∴ ∥ ( )
∴∠B= ( )
2、如图,已知CD∥AB,EF∥AB,求∠A+∠AEC+∠C的度数。
∵CD∥AB (已知)
∴∠1+∠A=180° ( )
∵CD∥AB,EF∥AB ( )
∴ ∥ ( )
∴∠2+∠C=180° ( )
∴∠1+∠A+∠2+∠C=360°(等式的性质)
即∠A+∠AEC+∠C=360°。
3、如图,已知AB∥CD,∠A+∠B=180°,∠A=∠D吗?为什么?
六、课外作业:(2分钟)
1、∵∠3+∠4=180°(已知)
∴ ∥ ( )
∴∠1= ( )
2、如图,
∵AB∥CD (已知)
∴ = ( )
∵∠1=∠2 ( )
∴ ∥ ( )
∴∠DAB+∠ABC=180°( )
3、如图,已知∠1=∠2=∠3=35°,求∠AED的度数。
分析:
(1)由∠1=∠2=∠3=35°,你能得到 。
(2)分析图形,你能得到什么?
(3)看结论,你能转化为什么问题?
(4)请写出解题过程。
解:
4、如图,已知∠1=∠2,则∠2=∠3吗?为什么?
