5.2 图形的运动 课件(共38张PPT)
文档属性
| 名称 | 5.2 图形的运动 课件(共38张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 18.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-10 19:30:39 | ||
图片预览








文档简介
(共38张PPT)
图形的运动
Motion of a figure
苏科版七年级上册第5章走进图形世界
教学目标
01
通过具体实例,从图形运动变化的角度感悟“点动成线”、“线动成面”、“面动成体”的形象,理解几何体是由点、线、面构成的
03
通过图案设计的“实验”,了解图形的翻折、平移和旋转等变化,初步探索图形间的变换关系
02
能正确识别出棱柱和棱锥,并描绘出它们的特征,意识到圆柱与棱柱、圆锥与棱锥的异同
旋转体
01
情境引入
已知:面与面相交得到线,线与线相交得到点
反之,点动起来会形成什么呢?线动起来又会形成什么呢?
请先观察图片,再回答问题~
点运动形成线
01
情境引入
我们所看到的流星雨可以看作是:
点运动形成的美丽的线
01
情境引入
线运动形成面
01
情境引入
汽车驾驶室前的雨刮器可以看成线:
当它来回刷洗车玻璃上的雨水时,就形成一个扇形面
01
情境引入
总结起来就是:点动成线,线动成面~
那么,新的问题又来了,面动起来会形成什么呢?
让我们一起来动手完成以下三个操作,再回答问题~
(1)长方形纸板绕它的一条边旋转1周;
(2)直角三角尺绕它的一条直角边旋转1周;
(3)一枚银币在桌面上竖直快速旋转.
01
情境引入
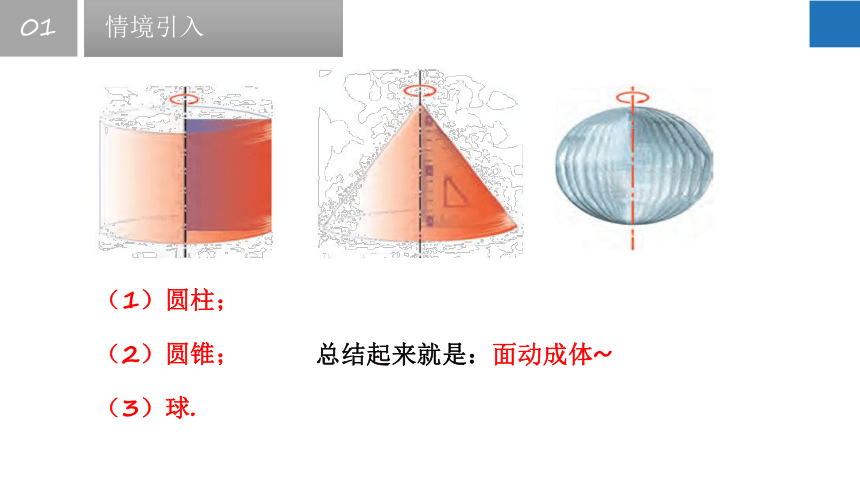
(1)圆柱;
(2)圆锥;
(3)球.
总结起来就是:面动成体~
02
知识精讲
点动成线,线动成面,面动成体~
几何体是由点、线、面组成的
02
知识精讲
认识圆柱、圆锥与球
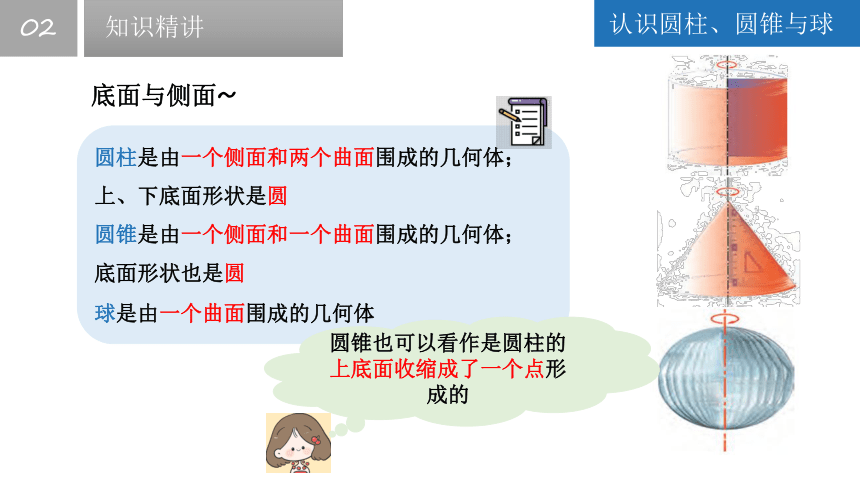
圆柱是由一个侧面和两个曲面围成的几何体;
上、下底面形状是圆
底面与侧面~
圆锥是由一个侧面和一个曲面围成的几何体;
底面形状也是圆
球是由一个曲面围成的几何体
圆锥也可以看作是圆柱的上底面收缩成了一个点形成的
02
知识精讲
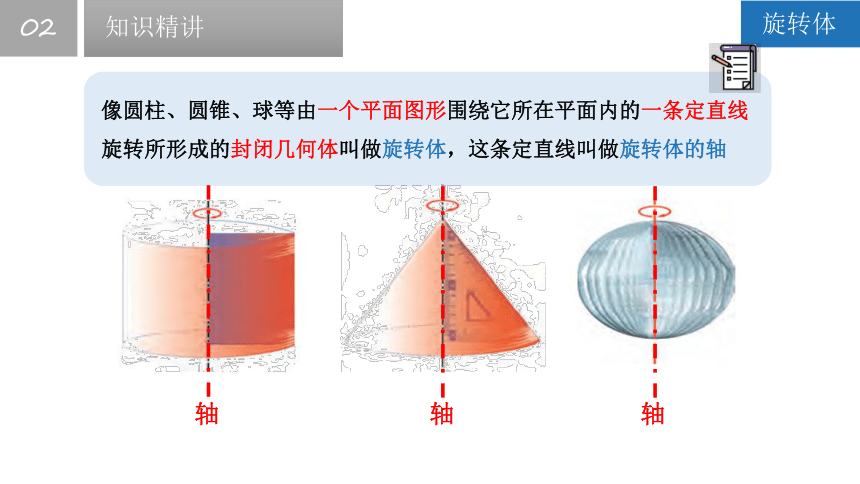
像圆柱、圆锥、球等由一个平面图形围绕它所在平面内的一条定直线旋转所形成的封闭几何体叫做旋转体,这条定直线叫做旋转体的轴
轴
轴
轴
旋转体
02
知识精讲
圆柱VS棱柱~
相同点:
不同点:
圆柱和棱柱的上、下底面相互平行,且能完全重合
(1)圆柱的底面形状是圆,棱柱的底面形状是多边形
(2)圆柱的侧面是曲面,棱柱的侧面是平行四边形
02
知识精讲
圆锥VS棱锥~
相同点:
不同点:
不算棱锥底面的顶点,圆锥和棱锥都只有一个顶点
(1)圆锥的底面形状是圆,棱锥的底面形状是多边形
(2)圆锥的侧面是曲面,棱锥的侧面是三角形
例1 “枪挑一条线,棍扫一大片”,从数学的角度解释为( )
A.点动成线,线动成面
B.线动成面,面动成体
C.点动成线,面动成体
D.点动成面,面动成线
A
例2 下列几何体中可以由平面图形绕某条直线旋转一周得到的是( )
A. B. C. D.
B
例3 我们知道,圆柱是由长方形绕着它的一边所在直线旋转一周得到的,下列绕着直线旋转一周能得到下图的是( )
A. B. C. D.
A
图形的翻折、平移
与旋转
Q1:将两块相同的直角三角尺相等的边拼在一起,可以拼成哪些不同的平面图形?你能说出这些图形的名称吗?
以斜边为公共边~
矩形
其他图形
01
情境引入
以短直角边为公共边~
等腰三角形
平行四边形
以长直角边为公共边~
等腰三角形
平行四边形
01
情境引入
Q2:在下图的空白方格中画出相应的图形,使直线两旁的图形完全相同
01
情境引入
翻折能设计出优美的图案~
图(1)虚线以下的部分向右平移2格
图(1)
图(2)
Q3-1:图(1)是由“ ”向右平移而成的.
把图(1)沿着虚线剪开,怎样改变图形的位置可以得到图(2)?
01
情境引入
Q3-2:图(1)虚线以下的部分向右平移4格,得到怎样的图形?
在图(3)中把它画出来.
图(1)
图(3)
01
情境引入
Q4:如何分别将下图中的三角尺旋转到图中虚线所示的位置?
O
(1)将三角尺绕着点O旋转180°
(2)将三角尺绕着点A顺时针旋转90°
(1)
(2)
A
01
情境引入
从以上4个实验探究中,我们可以感受到“翻折”、“平移”、“旋转”之美
02
知识精讲
“翻折”、“平移”、“旋转”是图形变换的三种基本类型
02
知识精讲
翻折的概念
翻折的定义:
翻折就是将一个图形沿着某一条直线翻折过来,直线两旁的部分能够相互重合
翻折的特点:
沿直线运动,位置改变,但形状、大小不变
02
知识精讲
平移的概念
平移的定义:
将一个图形沿着某个方向移动一定的距离,叫图形的平移
平移的距离是物体某个点到移动后相应的点的距离
平移的特点:
沿直线运动,位置改变,但形状、大小不变
02
知识精讲
旋转的概念
旋转的定义:
一个图形绕着一个定点旋转一定的角度得到另一个图形的变化,叫旋转
这个定点叫旋转中心
与时针旋转方向相同的是顺时针旋转,与时针旋转方向相反的是逆时针旋转
旋转的特点:
位置改变,但形状、大小不变
例4 如图的四个图形中,由基础图形通过平移、旋转或轴对称这三种变换都能得到的是( )
A. B. C. D.
B
例5 如图,在9×6的方格纸中,小树从位置A经过平移旋转后到达位置B,下列说法中正确的是( )
A.先向右平移6格,再绕点B顺时针旋转45°
B.先向右平移6格,再绕点B逆时针旋转45°
C.先向右平移6格,再绕点B顺时针旋转90°
D.先向右平移6格,再绕点B逆时针旋转90°
B
例6 如图,△ABC通过平移、轴对称或旋转得到△DEC,下列变换正确的是( )
A.△ABC绕点C顺时针旋转90°后再向左平移3个单位长度得△DEC
B.△ABC沿BC翻折后再绕点C逆时针旋转90°得到△DEC
C.△ABC沿AC翻折后再绕点C逆时针旋转90°得到△DEC
D.△ABC沿AC翻折后再绕点C顺时针旋转90°得到△DEC
C
A.× 修正:△ABC绕点C顺时针旋转90°沿EC翻折
B.× 修正:ABC沿BC翻折后再绕点C顺时针旋转90°
C.√
D.× 修正:见C
例7 一个图形无论经过翻折变换、平移变换还是旋转变换,下列结论一定正确的是__________.
(把所有你认为正确的序号都写上)
①对应线段平行;
②对应线段相等;
③对应角相等;
④图形的形状和大小都不变.
②③④
课后总结
点动成线,线动成面,面动成体~
几何体是由点、线、面组成的
圆柱、圆锥与球:
圆柱是由一个侧面和两个曲面围成的几何体;
上、下底面形状是圆
圆锥是由一个侧面和一个曲面围成的几何体;
底面形状也是圆
球是由一个曲面围成的几何体
像圆柱、圆锥、球等由一个平面图形围绕它所在平面内的一条定直线旋转所形成的封闭几何体叫做旋转体,这条定直线叫做旋转体的轴
课后总结
圆柱VS棱柱~
相同点:
圆柱和棱柱的上、下底面相互平行,且能完全重合
不同点:
(1)圆柱的底面形状是圆,棱柱的底面形状是多边形
(2)圆柱的侧面是曲面,棱柱的侧面是平行四边形
圆锥VS棱锥~
相同点:
不算棱锥底面的顶点,圆锥和棱锥都只有一个顶点
不同点:
(1)圆锥的底面形状是圆,棱锥的底面形状是多边形
(2)圆锥的侧面是曲面,棱锥的侧面是三角形
课后总结
“翻折”、“平移”、“旋转”是图形变换的三种基本类型
翻折的定义:
翻折就是将一个图形沿着某一条直线翻折过来,直线两旁的部分能够相互重合
翻折的特点:
沿直线运动,位置改变,但形状、大小不变
课后总结
平移的定义:
将一个图形沿着某个方向移动一定的距离,叫图形的平移
平移的距离是物体某个点到移动后相应的点的距离
平移的特点:
沿直线运动,位置改变,但形状、大小不变
旋转的定义:
一个图形绕着一个定点旋转一定的角度得到另一个图形的变化,叫旋转
这个定点叫旋转中心
与时针旋转方向相同的是顺时针旋转,与时针旋转方向相反的是逆时针旋转
旋转的特点:
位置改变,但形状、大小不变
课后预习
几何体是由点、线、面组成的,要深刻地去认识一个几何体,我们还需对它进行“解剖”,把它的一个个“部分”放到我们熟悉的平面领域来探究~
或者大家可以先来思考这样一个小问题:
用一把刀去切圆柱,你能得到什么样形状的图形呢?
谢谢学习
Thank you for learning
图形的运动
Motion of a figure
苏科版七年级上册第5章走进图形世界
教学目标
01
通过具体实例,从图形运动变化的角度感悟“点动成线”、“线动成面”、“面动成体”的形象,理解几何体是由点、线、面构成的
03
通过图案设计的“实验”,了解图形的翻折、平移和旋转等变化,初步探索图形间的变换关系
02
能正确识别出棱柱和棱锥,并描绘出它们的特征,意识到圆柱与棱柱、圆锥与棱锥的异同
旋转体
01
情境引入
已知:面与面相交得到线,线与线相交得到点
反之,点动起来会形成什么呢?线动起来又会形成什么呢?
请先观察图片,再回答问题~
点运动形成线
01
情境引入
我们所看到的流星雨可以看作是:
点运动形成的美丽的线
01
情境引入
线运动形成面
01
情境引入
汽车驾驶室前的雨刮器可以看成线:
当它来回刷洗车玻璃上的雨水时,就形成一个扇形面
01
情境引入
总结起来就是:点动成线,线动成面~
那么,新的问题又来了,面动起来会形成什么呢?
让我们一起来动手完成以下三个操作,再回答问题~
(1)长方形纸板绕它的一条边旋转1周;
(2)直角三角尺绕它的一条直角边旋转1周;
(3)一枚银币在桌面上竖直快速旋转.
01
情境引入
(1)圆柱;
(2)圆锥;
(3)球.
总结起来就是:面动成体~
02
知识精讲
点动成线,线动成面,面动成体~
几何体是由点、线、面组成的
02
知识精讲
认识圆柱、圆锥与球
圆柱是由一个侧面和两个曲面围成的几何体;
上、下底面形状是圆
底面与侧面~
圆锥是由一个侧面和一个曲面围成的几何体;
底面形状也是圆
球是由一个曲面围成的几何体
圆锥也可以看作是圆柱的上底面收缩成了一个点形成的
02
知识精讲
像圆柱、圆锥、球等由一个平面图形围绕它所在平面内的一条定直线旋转所形成的封闭几何体叫做旋转体,这条定直线叫做旋转体的轴
轴
轴
轴
旋转体
02
知识精讲
圆柱VS棱柱~
相同点:
不同点:
圆柱和棱柱的上、下底面相互平行,且能完全重合
(1)圆柱的底面形状是圆,棱柱的底面形状是多边形
(2)圆柱的侧面是曲面,棱柱的侧面是平行四边形
02
知识精讲
圆锥VS棱锥~
相同点:
不同点:
不算棱锥底面的顶点,圆锥和棱锥都只有一个顶点
(1)圆锥的底面形状是圆,棱锥的底面形状是多边形
(2)圆锥的侧面是曲面,棱锥的侧面是三角形
例1 “枪挑一条线,棍扫一大片”,从数学的角度解释为( )
A.点动成线,线动成面
B.线动成面,面动成体
C.点动成线,面动成体
D.点动成面,面动成线
A
例2 下列几何体中可以由平面图形绕某条直线旋转一周得到的是( )
A. B. C. D.
B
例3 我们知道,圆柱是由长方形绕着它的一边所在直线旋转一周得到的,下列绕着直线旋转一周能得到下图的是( )
A. B. C. D.
A
图形的翻折、平移
与旋转
Q1:将两块相同的直角三角尺相等的边拼在一起,可以拼成哪些不同的平面图形?你能说出这些图形的名称吗?
以斜边为公共边~
矩形
其他图形
01
情境引入
以短直角边为公共边~
等腰三角形
平行四边形
以长直角边为公共边~
等腰三角形
平行四边形
01
情境引入
Q2:在下图的空白方格中画出相应的图形,使直线两旁的图形完全相同
01
情境引入
翻折能设计出优美的图案~
图(1)虚线以下的部分向右平移2格
图(1)
图(2)
Q3-1:图(1)是由“ ”向右平移而成的.
把图(1)沿着虚线剪开,怎样改变图形的位置可以得到图(2)?
01
情境引入
Q3-2:图(1)虚线以下的部分向右平移4格,得到怎样的图形?
在图(3)中把它画出来.
图(1)
图(3)
01
情境引入
Q4:如何分别将下图中的三角尺旋转到图中虚线所示的位置?
O
(1)将三角尺绕着点O旋转180°
(2)将三角尺绕着点A顺时针旋转90°
(1)
(2)
A
01
情境引入
从以上4个实验探究中,我们可以感受到“翻折”、“平移”、“旋转”之美
02
知识精讲
“翻折”、“平移”、“旋转”是图形变换的三种基本类型
02
知识精讲
翻折的概念
翻折的定义:
翻折就是将一个图形沿着某一条直线翻折过来,直线两旁的部分能够相互重合
翻折的特点:
沿直线运动,位置改变,但形状、大小不变
02
知识精讲
平移的概念
平移的定义:
将一个图形沿着某个方向移动一定的距离,叫图形的平移
平移的距离是物体某个点到移动后相应的点的距离
平移的特点:
沿直线运动,位置改变,但形状、大小不变
02
知识精讲
旋转的概念
旋转的定义:
一个图形绕着一个定点旋转一定的角度得到另一个图形的变化,叫旋转
这个定点叫旋转中心
与时针旋转方向相同的是顺时针旋转,与时针旋转方向相反的是逆时针旋转
旋转的特点:
位置改变,但形状、大小不变
例4 如图的四个图形中,由基础图形通过平移、旋转或轴对称这三种变换都能得到的是( )
A. B. C. D.
B
例5 如图,在9×6的方格纸中,小树从位置A经过平移旋转后到达位置B,下列说法中正确的是( )
A.先向右平移6格,再绕点B顺时针旋转45°
B.先向右平移6格,再绕点B逆时针旋转45°
C.先向右平移6格,再绕点B顺时针旋转90°
D.先向右平移6格,再绕点B逆时针旋转90°
B
例6 如图,△ABC通过平移、轴对称或旋转得到△DEC,下列变换正确的是( )
A.△ABC绕点C顺时针旋转90°后再向左平移3个单位长度得△DEC
B.△ABC沿BC翻折后再绕点C逆时针旋转90°得到△DEC
C.△ABC沿AC翻折后再绕点C逆时针旋转90°得到△DEC
D.△ABC沿AC翻折后再绕点C顺时针旋转90°得到△DEC
C
A.× 修正:△ABC绕点C顺时针旋转90°沿EC翻折
B.× 修正:ABC沿BC翻折后再绕点C顺时针旋转90°
C.√
D.× 修正:见C
例7 一个图形无论经过翻折变换、平移变换还是旋转变换,下列结论一定正确的是__________.
(把所有你认为正确的序号都写上)
①对应线段平行;
②对应线段相等;
③对应角相等;
④图形的形状和大小都不变.
②③④
课后总结
点动成线,线动成面,面动成体~
几何体是由点、线、面组成的
圆柱、圆锥与球:
圆柱是由一个侧面和两个曲面围成的几何体;
上、下底面形状是圆
圆锥是由一个侧面和一个曲面围成的几何体;
底面形状也是圆
球是由一个曲面围成的几何体
像圆柱、圆锥、球等由一个平面图形围绕它所在平面内的一条定直线旋转所形成的封闭几何体叫做旋转体,这条定直线叫做旋转体的轴
课后总结
圆柱VS棱柱~
相同点:
圆柱和棱柱的上、下底面相互平行,且能完全重合
不同点:
(1)圆柱的底面形状是圆,棱柱的底面形状是多边形
(2)圆柱的侧面是曲面,棱柱的侧面是平行四边形
圆锥VS棱锥~
相同点:
不算棱锥底面的顶点,圆锥和棱锥都只有一个顶点
不同点:
(1)圆锥的底面形状是圆,棱锥的底面形状是多边形
(2)圆锥的侧面是曲面,棱锥的侧面是三角形
课后总结
“翻折”、“平移”、“旋转”是图形变换的三种基本类型
翻折的定义:
翻折就是将一个图形沿着某一条直线翻折过来,直线两旁的部分能够相互重合
翻折的特点:
沿直线运动,位置改变,但形状、大小不变
课后总结
平移的定义:
将一个图形沿着某个方向移动一定的距离,叫图形的平移
平移的距离是物体某个点到移动后相应的点的距离
平移的特点:
沿直线运动,位置改变,但形状、大小不变
旋转的定义:
一个图形绕着一个定点旋转一定的角度得到另一个图形的变化,叫旋转
这个定点叫旋转中心
与时针旋转方向相同的是顺时针旋转,与时针旋转方向相反的是逆时针旋转
旋转的特点:
位置改变,但形状、大小不变
课后预习
几何体是由点、线、面组成的,要深刻地去认识一个几何体,我们还需对它进行“解剖”,把它的一个个“部分”放到我们熟悉的平面领域来探究~
或者大家可以先来思考这样一个小问题:
用一把刀去切圆柱,你能得到什么样形状的图形呢?
谢谢学习
Thank you for learning
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
