4.4.2 探索三角形相似的条件(第2课时) 课件(共24张PPT)
文档属性
| 名称 | 4.4.2 探索三角形相似的条件(第2课时) 课件(共24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-09 16:39:40 | ||
图片预览





文档简介
(共24张PPT)
北师大版 九年级上册
4.4.2 探索三角形相似的条件(第2课时)
学习目标
1.理解并掌握三角形相似的判定定理:“两边对应成比例且夹角相等的两个三角形相似”.
2.会运用三角形相似的判定方法解决简单问题.
情境导入
请给出从这些判定三角形相似的六个条件中选出两个条件的组合还有哪些?这些条件能否判定两个三角相似?
边
角
边
角
角
边
只有两角分别相等的两个三角形相似
探究新知
核心知识点一:
相似三角形的判定定理2
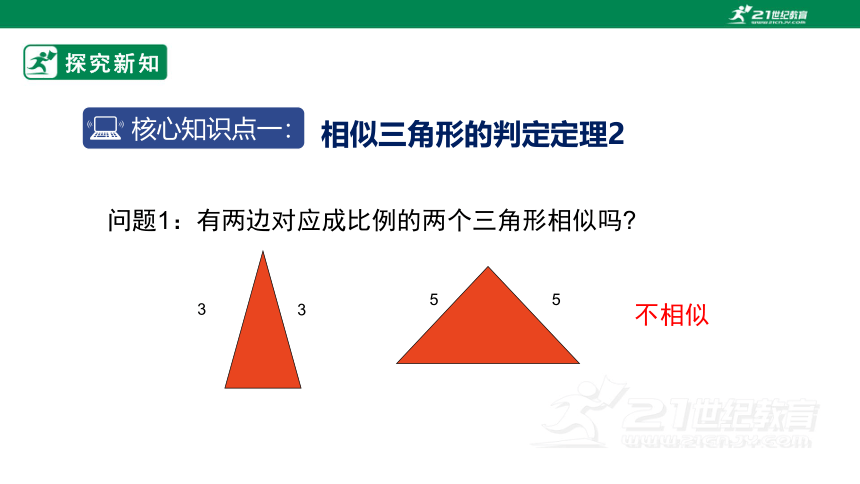
问题1:有两边对应成比例的两个三角形相似吗
3
3
5
5
不相似
探究新知
问题2:类比三角形全等的判定方法(SAS),猜想可以添加什么条件来判定两个三角形相似?
3
3
5
5
角相等?
探究新知
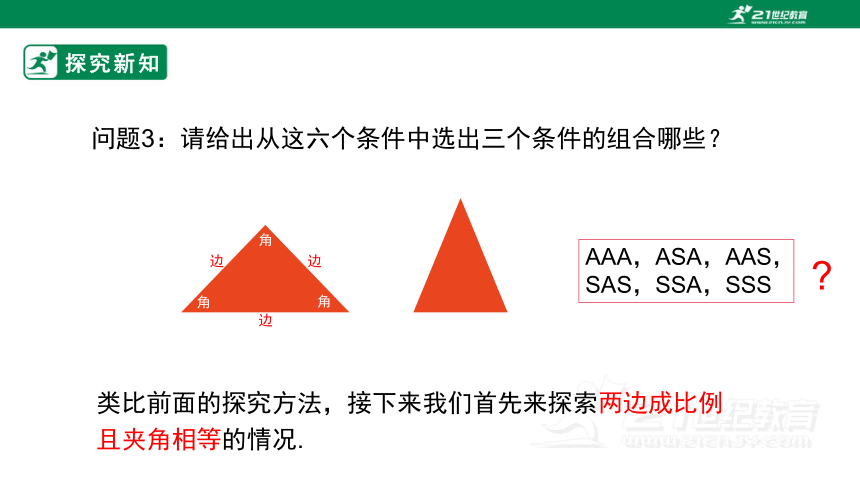
问题3:请给出从这六个条件中选出三个条件的组合哪些?
边
角
边
角
角
边
类比前面的探究方法,接下来我们首先来探索两边成比例且夹角相等的情况.
AAA,ASA,AAS,SAS,SSA,SSS
探究新知
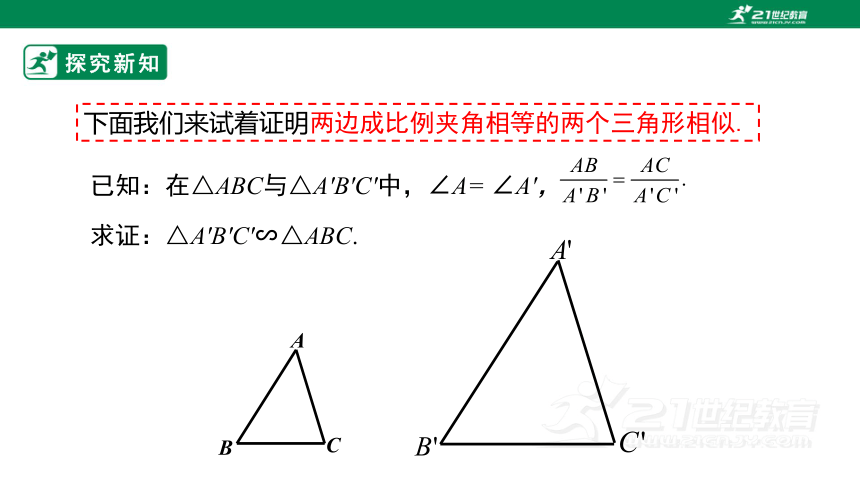
下面我们来试着证明两边成比例夹角相等的两个三角形相似.
已知:在△ABC与△A′B′C′中,∠A= ∠A′,
求证:△A′B′C′∽△ABC.
A
B
C
探究新知
A
B
C
D
E
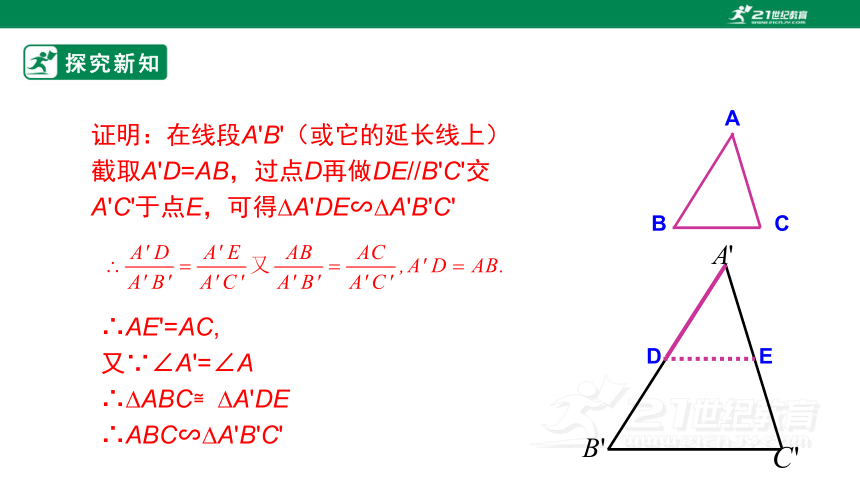
证明:在线段A'B'(或它的延长线上)截取A'D=AB,过点D再做DE//B'C'交A'C'于点E,可得 A'DE∽ A'B'C'
∴AE'=AC,
又∵∠A'=∠A
∴ ABC≌ A'DE
∴ABC∽ A'B'C'
探究新知
归纳总结
如果两个三角形的两组对应边的比相等,并且相应的夹角相等,那么这两个三角形相似。
相似三角形判定定理2:
几何语言:
∵
∴△ABC∽△A′B′C′
A
B
C
A '
B '
C '
探究新知
两边成比例且其中一边所对的角相等,那么这两个三角形不一定相似.
想一想: 如果△ABC 与△A'B'C' 两边成比例,且其中一边所对的角相等,那么这两个三角形一定相似吗?
小明和小颖分别画出了如图所示的三角形.由此你能得到什么结论?
探究新知
例1: 如图,D,E分别是 △ABC 的边 AC,AB 上的点,AE=1.5,AC=2,BC=3,且 ,求 DE 的长.
解:∵ AE=1.5,AC=2,
∴
又∵∠EAD=∠CAB,
∴ △ADE ∽△ABC,
∴
∴
提示:
解题时要找准对应边.
A
C
B
E
D
探究新知
解:(1)证明:∵CD是边AB上的高
∴∠ADC=∠CDB=90°
又CD2=AD·BD
∴
∴△ACD∽△CBD
探究新知
(2)∵△ACD∽△CBD
∴∠A=∠BCD.
在△ACD中,∠ADC=90°,
∴∠A+∠ACD=90°,
∴∠BCD+∠ACD=90°.
即∠ACB=90°.
随堂练习
1.下列条件能判断△ABC和△A′B′C′相似的是( )
C
随堂练习
2.如图,每个小正方形边长均为1,则下列图中的三角形(阴影部分)与右图中△ABC相似的是( )
A
B
C
D
B
随堂练习
3.如图,△ABC中∠ACB=90o,CD⊥AB于D。则图中能够相似的三角形共有( )
A.1对 B.2对
C.3对 D.4对
C
随堂练习
4.△ABC中,D是AB上一固定点。E是AC上的一个动点,若使△ABC和△ADE相似,则这样的点E有( )
A.1个 B.2个 C.3个 D.很多
B
随堂练习
5.如图,在△ABC中,D,E分别为AC,AB上的点,且∠ADE=∠B,AE=3,BE=4,则AD·AC=_______.
21
随堂练习
6.如图,正方形ABCD中,E为AB中点,BF= BC,那么图中与△ADE相似的三角形有____________.
△BEF,△EDF
随堂练习
7. 如图,∠DAB =∠CAE,且 AB · AD = AE·AC,
求证 △ABC ∽△AED.
证明:∵ AB · AD = AE·AC,
∴
又∵ ∠DAB =∠CAE,
∴∠ DAB +∠BAE =∠CAE +∠BAE ,
即∠DAE =∠BAC,
∴ △ABC ∽△AED.
A
B
C
D
E
随堂练习
8.△ABC为锐角三角形,BD、CE为高 . 求证:△ ADE∽ △ ABC.
证明:∵BD⊥AC,CE⊥AB,
∴∠ABD+∠A=90°,
∠ACE+∠A= 90°.
∴ ∠ABD= ∠ACE.
又∵ ∠A= ∠A,
∴△ ABD ∽ △ ACE.
∴
∵ ∠A= ∠A,
∴ △ ADE ∽ △ ABC.
A
B
D
C
E
O
课堂小结
这节课我们学习了哪些知识?
判定定理二:两边成比例且夹角相等的两个三角形相似.
∠B=∠B '
∴ △ABC∽△A ' B ' C '
∵ 在△ABC与△A ' B ' C ' 中
A
B
C
A '
B '
C '
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
北师大版 九年级上册
4.4.2 探索三角形相似的条件(第2课时)
学习目标
1.理解并掌握三角形相似的判定定理:“两边对应成比例且夹角相等的两个三角形相似”.
2.会运用三角形相似的判定方法解决简单问题.
情境导入
请给出从这些判定三角形相似的六个条件中选出两个条件的组合还有哪些?这些条件能否判定两个三角相似?
边
角
边
角
角
边
只有两角分别相等的两个三角形相似
探究新知
核心知识点一:
相似三角形的判定定理2
问题1:有两边对应成比例的两个三角形相似吗
3
3
5
5
不相似
探究新知
问题2:类比三角形全等的判定方法(SAS),猜想可以添加什么条件来判定两个三角形相似?
3
3
5
5
角相等?
探究新知
问题3:请给出从这六个条件中选出三个条件的组合哪些?
边
角
边
角
角
边
类比前面的探究方法,接下来我们首先来探索两边成比例且夹角相等的情况.
AAA,ASA,AAS,SAS,SSA,SSS
探究新知
下面我们来试着证明两边成比例夹角相等的两个三角形相似.
已知:在△ABC与△A′B′C′中,∠A= ∠A′,
求证:△A′B′C′∽△ABC.
A
B
C
探究新知
A
B
C
D
E
证明:在线段A'B'(或它的延长线上)截取A'D=AB,过点D再做DE//B'C'交A'C'于点E,可得 A'DE∽ A'B'C'
∴AE'=AC,
又∵∠A'=∠A
∴ ABC≌ A'DE
∴ABC∽ A'B'C'
探究新知
归纳总结
如果两个三角形的两组对应边的比相等,并且相应的夹角相等,那么这两个三角形相似。
相似三角形判定定理2:
几何语言:
∵
∴△ABC∽△A′B′C′
A
B
C
A '
B '
C '
探究新知
两边成比例且其中一边所对的角相等,那么这两个三角形不一定相似.
想一想: 如果△ABC 与△A'B'C' 两边成比例,且其中一边所对的角相等,那么这两个三角形一定相似吗?
小明和小颖分别画出了如图所示的三角形.由此你能得到什么结论?
探究新知
例1: 如图,D,E分别是 △ABC 的边 AC,AB 上的点,AE=1.5,AC=2,BC=3,且 ,求 DE 的长.
解:∵ AE=1.5,AC=2,
∴
又∵∠EAD=∠CAB,
∴ △ADE ∽△ABC,
∴
∴
提示:
解题时要找准对应边.
A
C
B
E
D
探究新知
解:(1)证明:∵CD是边AB上的高
∴∠ADC=∠CDB=90°
又CD2=AD·BD
∴
∴△ACD∽△CBD
探究新知
(2)∵△ACD∽△CBD
∴∠A=∠BCD.
在△ACD中,∠ADC=90°,
∴∠A+∠ACD=90°,
∴∠BCD+∠ACD=90°.
即∠ACB=90°.
随堂练习
1.下列条件能判断△ABC和△A′B′C′相似的是( )
C
随堂练习
2.如图,每个小正方形边长均为1,则下列图中的三角形(阴影部分)与右图中△ABC相似的是( )
A
B
C
D
B
随堂练习
3.如图,△ABC中∠ACB=90o,CD⊥AB于D。则图中能够相似的三角形共有( )
A.1对 B.2对
C.3对 D.4对
C
随堂练习
4.△ABC中,D是AB上一固定点。E是AC上的一个动点,若使△ABC和△ADE相似,则这样的点E有( )
A.1个 B.2个 C.3个 D.很多
B
随堂练习
5.如图,在△ABC中,D,E分别为AC,AB上的点,且∠ADE=∠B,AE=3,BE=4,则AD·AC=_______.
21
随堂练习
6.如图,正方形ABCD中,E为AB中点,BF= BC,那么图中与△ADE相似的三角形有____________.
△BEF,△EDF
随堂练习
7. 如图,∠DAB =∠CAE,且 AB · AD = AE·AC,
求证 △ABC ∽△AED.
证明:∵ AB · AD = AE·AC,
∴
又∵ ∠DAB =∠CAE,
∴∠ DAB +∠BAE =∠CAE +∠BAE ,
即∠DAE =∠BAC,
∴ △ABC ∽△AED.
A
B
C
D
E
随堂练习
8.△ABC为锐角三角形,BD、CE为高 . 求证:△ ADE∽ △ ABC.
证明:∵BD⊥AC,CE⊥AB,
∴∠ABD+∠A=90°,
∠ACE+∠A= 90°.
∴ ∠ABD= ∠ACE.
又∵ ∠A= ∠A,
∴△ ABD ∽ △ ACE.
∴
∵ ∠A= ∠A,
∴ △ ADE ∽ △ ABC.
A
B
D
C
E
O
课堂小结
这节课我们学习了哪些知识?
判定定理二:两边成比例且夹角相等的两个三角形相似.
∠B=∠B '
∴ △ABC∽△A ' B ' C '
∵ 在△ABC与△A ' B ' C ' 中
A
B
C
A '
B '
C '
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
