平行线期末复习[下学期]
文档属性
| 名称 | 平行线期末复习[下学期] |  | |
| 格式 | rar | ||
| 文件大小 | 765.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-06-13 13:56:00 | ||
图片预览




文档简介
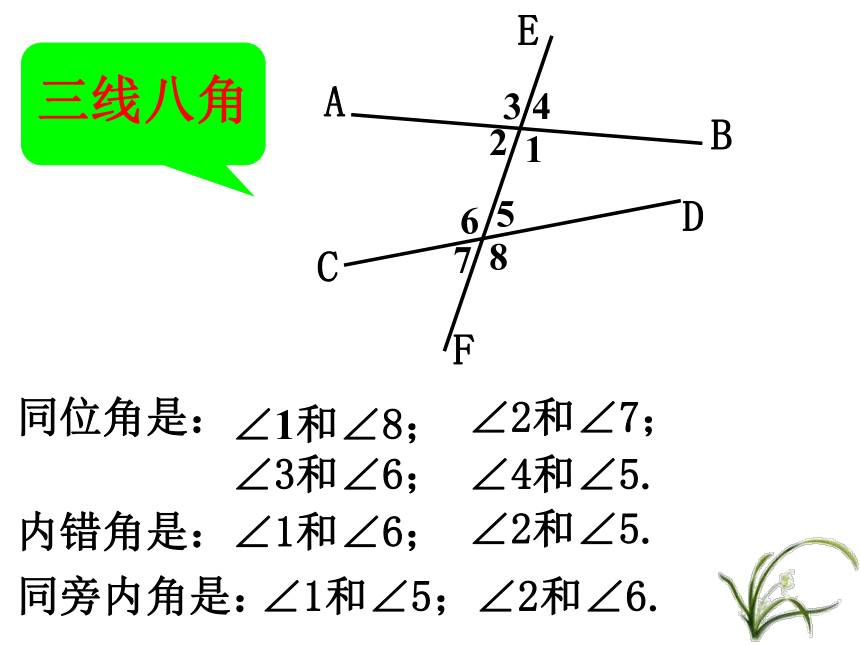
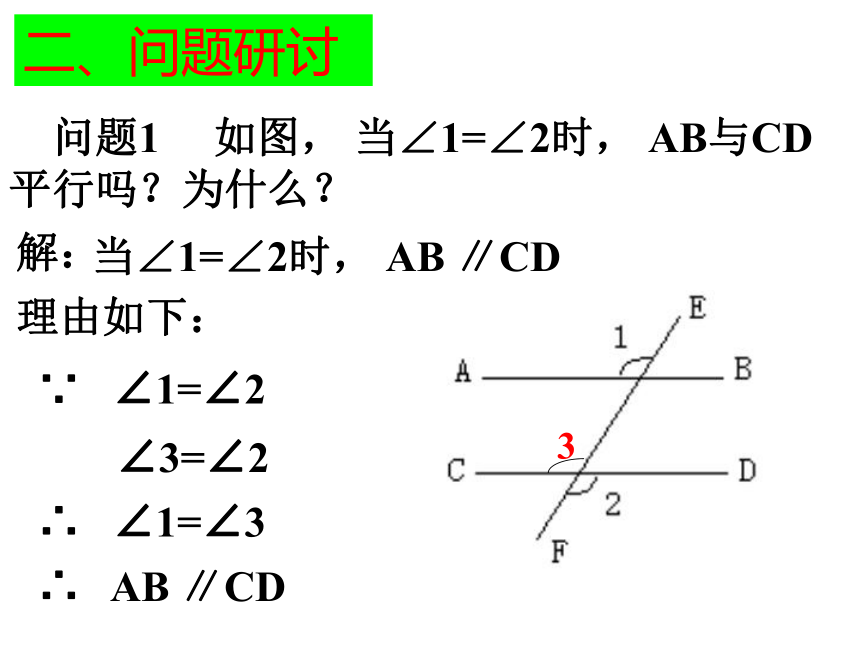
课件18张PPT。第二课 平行线复习第一课 相交线、垂线复习泽国第三中学 在同一平面内,两条不相交的直线叫做平行线记作:AB∥CD同位角是:∠1和∠8;∠2和∠7;∠3和∠6;∠4和∠5.内错角是:∠1和∠6;∠2和∠5.同旁内角是:∠1和∠5;∠2和∠6.一、知识回顾 平行线的判定: 1、同位角相等,两直线平行。2、内错角相等,两直线平行。3、同旁内角互补,两直线平行。4、平行于同一条直线的两条直线平行。(平行线的传递性) 一、知识回顾 平行线的性质: 1、两直线平行,同位角相等。2、两直线平行,内错角相等。3、两直线平行,同旁内角互补。 二、问题研讨 问题1 如图, 当∠1=∠2时, AB与CD
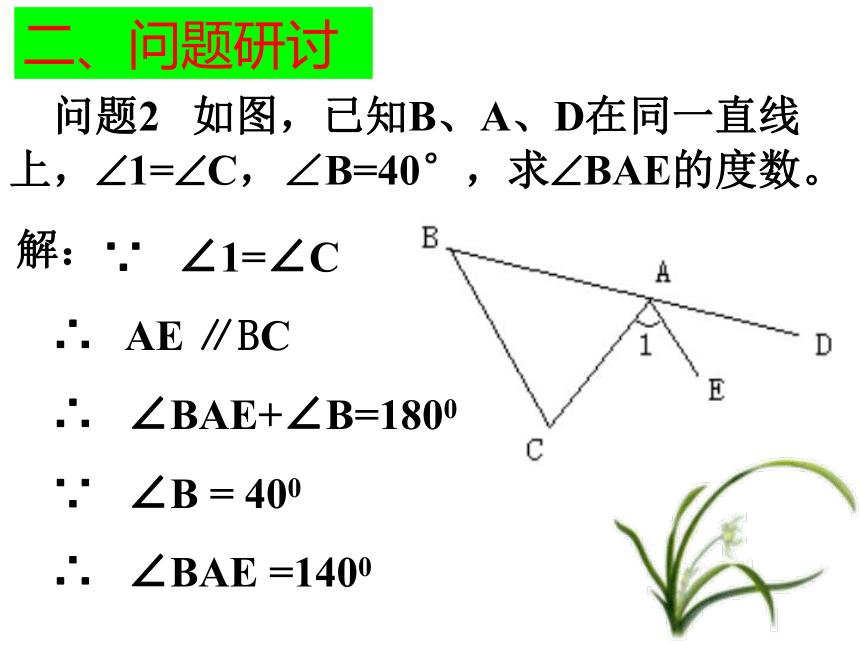
平行吗?为什么? 解:当∠1=∠2时, AB ∥CD理由如下:∵ ∠1=∠2 ∠3=∠2 ∴ ∠1=∠3 ∴ AB ∥CD二、问题研讨 问题2 如图,已知B、A、D在同一直线
上,?1=?C,∠B=40°,求?BAE的度数。 解:∵ ∠1=∠C ∴ AE ∥BC∴ ∠BAE+∠B=1800 ∵ ∠B = 400 ∴ ∠BAE =1400 问题3 已知:如图,
?1=?2=?B,EF∥AB。
问:?3和?C有什么数
量关系?为什么 ?∴ ?3=?C( ) 填空:∵?1=?B( )已知∴DE∥BC( )同位角相等,两直线平行∴?2=?C( )两直线平行,同位角相等∵ EF∥AB( ) 已知∴?B=?3( ) 两直线平行,同位角相等∵?2=?B( )已知等量代换三、课堂练习(1)两条直线被第三条直线所截,同位角相等 ( )1. 判断题:(2)同旁内角互补 ( )× × × 三、课堂练习2. 填空:如图
∵∠1=∠C (已知 )
∴AE∥BC ( )
∴∠2=∠B ( )∠EAC+∠C=180( )
前一步用的是平行线的_______,
后一步用的是 。 同位角相等,两直线平行两直线平行,内错角相等两直线平行,同旁内角互补判定平行线的性质三、课堂练习 3、小明在一张白纸上,先画一条直线,再画这条直线的平行线,然后依次画前 一条直线的平行线,当他画到第十条时, 第十条直线与第一条直线 , 理由是 。 平行平行线的传递性三、课堂练习0个、1个、2个 或 3个A三、课堂练习6、 l1,l2,l3为同一平面内的三条直线,若l1与l2不平行,l2与l3不平行,下列判断正确的是 ( )A、l1与l3一定不平行; B、l1与l3一定平行; C、l1与l3一定垂直; D、l1与l3可能相交,也可能平行。D三、课堂练习7、下列结论中,正确的个数是( )。
⑴在同一平面内不相交的两条线段必平行;⑵在同一平面内不相交的两条直线必平行;⑶在同一平面内不平行的两条线段必相交;⑷在同一平面内不平行的两条直线必相交。
(A) 1个 (B) 2个
(C) 3个 (D) 4个。 B8.如图,DE∥BC,∠D∶∠DBC = 2∶1,∠1 =∠2,求∠DEB的度数。
解:∵ DE∥BC ∴ ?E = ?1∠D+∠DBC=1800∵ ?D =2?DBC∴ ?DBC = 600∵ ?1 = ?2∴ ?E = 300四、课外作业作业(2)
复习题再 见祝大家学习愉快再见!
平行吗?为什么? 解:当∠1=∠2时, AB ∥CD理由如下:∵ ∠1=∠2 ∠3=∠2 ∴ ∠1=∠3 ∴ AB ∥CD二、问题研讨 问题2 如图,已知B、A、D在同一直线
上,?1=?C,∠B=40°,求?BAE的度数。 解:∵ ∠1=∠C ∴ AE ∥BC∴ ∠BAE+∠B=1800 ∵ ∠B = 400 ∴ ∠BAE =1400 问题3 已知:如图,
?1=?2=?B,EF∥AB。
问:?3和?C有什么数
量关系?为什么 ?∴ ?3=?C( ) 填空:∵?1=?B( )已知∴DE∥BC( )同位角相等,两直线平行∴?2=?C( )两直线平行,同位角相等∵ EF∥AB( ) 已知∴?B=?3( ) 两直线平行,同位角相等∵?2=?B( )已知等量代换三、课堂练习(1)两条直线被第三条直线所截,同位角相等 ( )1. 判断题:(2)同旁内角互补 ( )× × × 三、课堂练习2. 填空:如图
∵∠1=∠C (已知 )
∴AE∥BC ( )
∴∠2=∠B ( )∠EAC+∠C=180( )
前一步用的是平行线的_______,
后一步用的是 。 同位角相等,两直线平行两直线平行,内错角相等两直线平行,同旁内角互补判定平行线的性质三、课堂练习 3、小明在一张白纸上,先画一条直线,再画这条直线的平行线,然后依次画前 一条直线的平行线,当他画到第十条时, 第十条直线与第一条直线 , 理由是 。 平行平行线的传递性三、课堂练习0个、1个、2个 或 3个A三、课堂练习6、 l1,l2,l3为同一平面内的三条直线,若l1与l2不平行,l2与l3不平行,下列判断正确的是 ( )A、l1与l3一定不平行; B、l1与l3一定平行; C、l1与l3一定垂直; D、l1与l3可能相交,也可能平行。D三、课堂练习7、下列结论中,正确的个数是( )。
⑴在同一平面内不相交的两条线段必平行;⑵在同一平面内不相交的两条直线必平行;⑶在同一平面内不平行的两条线段必相交;⑷在同一平面内不平行的两条直线必相交。
(A) 1个 (B) 2个
(C) 3个 (D) 4个。 B8.如图,DE∥BC,∠D∶∠DBC = 2∶1,∠1 =∠2,求∠DEB的度数。
解:∵ DE∥BC ∴ ?E = ?1∠D+∠DBC=1800∵ ?D =2?DBC∴ ?DBC = 600∵ ?1 = ?2∴ ?E = 300四、课外作业作业(2)
复习题再 见祝大家学习愉快再见!
