平行线复习[下学期]
图片预览





文档简介
课件19张PPT。平行线(一)知识点一、平行线的意义1。平行线的定义: 在同一平面内,不相交的两条直线叫平行线。2。同一平面内,两条直线的位置关系:在同一平面内,两条直线的位置关系只有相交和平行两种。3。平行公理: 如果两条直线都与第三条直线平行,那么这两条直线,也互相平行。数学形式:图形形式:∵a∥c,b∥c,∴a∥b文字形式:文字语言符号语言图形语言例1、下列说法正确的是( )
A、同一平面内不相交的两条射线是平行线。
B、同一平面内不相交的两条线是平行线。
C、同一平面内不相交的两条直线是平行线。
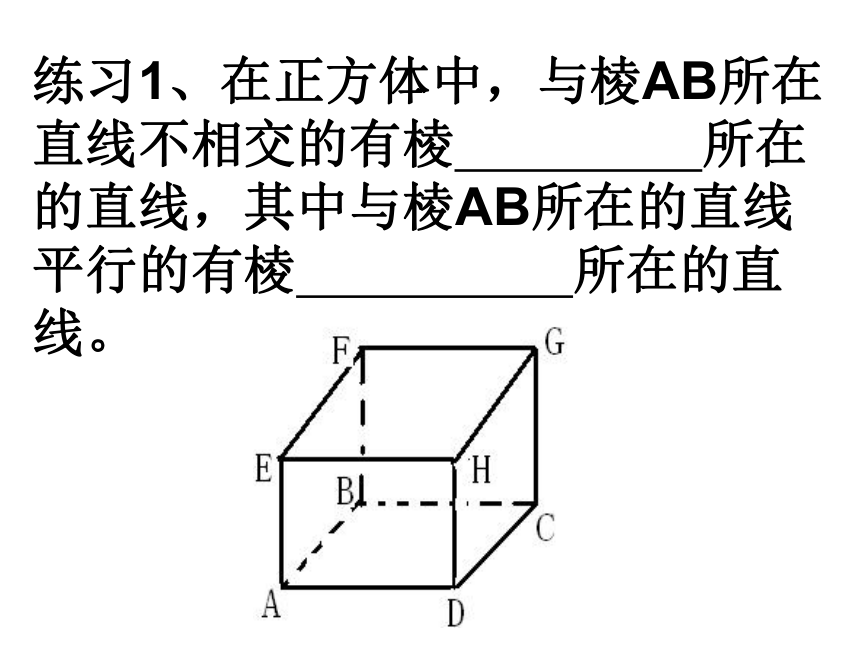
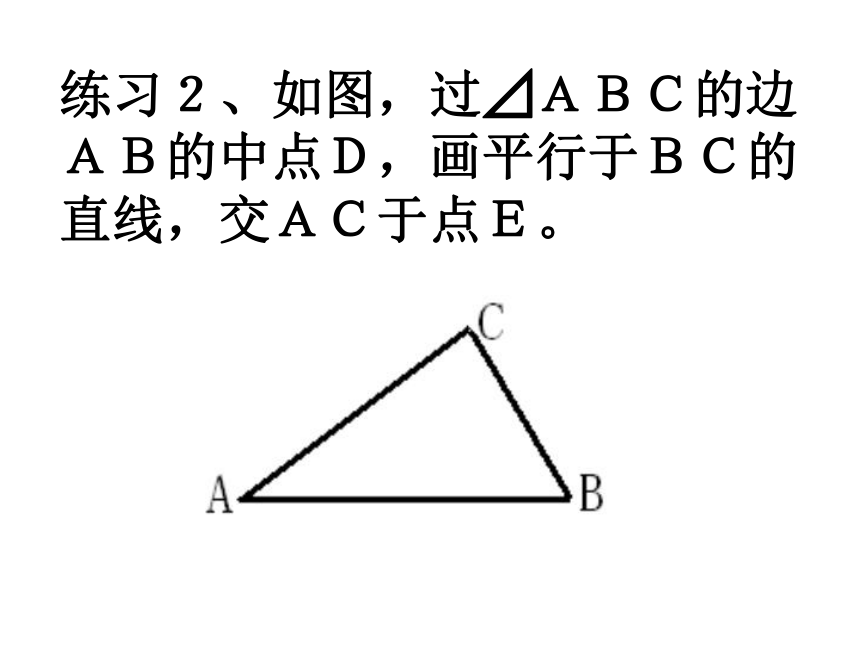
D、不相交的两条直线是平行线。C练习1、在正方体中,与棱AB所在直线不相交的有棱 所在的直线,其中与棱AB所在的直线平行的有棱 所在的直线。例2、阅读下面的语句,并画出符合题意的图形:(1)直线AB、CD是相交直线,点P是直线AB外一点,直线EF经过P点与与直线AB平行,与直线CD相交于E;(2)点P是直线AB外一点,直线CD经过点P,且与直线AB平行。练习2、如图,过⊿ABC的边AB的中点D,画平行于BC的直线,交AC于点E。知识点二、两直线平行的条件1、同位角、内错角、同旁内角的概念关键点提示:首先要确定这一对角是由哪两条直线被哪一条直线所截而形成的,然后再看它们的位置关系,并由此位置关系确定它们是一对什么角。2。直线平行的条件:定理1、同位角相等,两直线平行。文字形式∵∠1=∠5∴AB∥CD数学形式:图形形式: 请你用三种形式理解另两种类似的平行判定的条件。例3、如图,直线BC、DE被直线AB所截。
(1) ∠1与 ∠2, ∠1与 ∠3, ∠1与 ∠4各是一对什么角?
(2)如果 ∠1= ∠4,那么 ∠1与 ∠2相等吗? ∠1与 ∠3有什么关系?练习3、如图,与∠1是同位角的是 ,与∠1是内错角的是 ,与∠1是同旁内角的是 。例4、如图,已知m1与m2、m3相交于A、B两点,若∠1=30°,∠2=150°,试说明m2∥m3, 练习4、如图,如果∠1=47°,∠2=133°,∠D=47°,那么BC与DE平行吗?AB与CD呢?例5、如果两条直线都垂直于同一条直线,那么这两条直线平行吗?为什么?练习5、判断:
(1)∵a∥c,b∥c,∴a∥b(2) ∵a⊥c,b⊥c,∴a⊥b疑难解析 疑点:由“同位角相等,两直线平行”,你能得到“内错角相等,两直线平行”、“同旁内角互补,两直线平行” 规律:遇到一个新问题时,常常把它转化为已知的(或已经解决的)问题来解决,这是一种重要的数学思想。例6、已知,如图,BE平分∠ABC,∠1=∠3,试说明:BC∥DE疑难解析疑难解析 难点:已知几何基本图形不是我们所学过的“三线八角”基本图形,需添加一些辅助线把它转化成我们熟悉的图形。疑难解析例8、已知,如图,AB∥CD,P是AB、CD之间的一点,已知∠B=32°,∠C=25°,求∠BPC的度数。挑战自我?
(第12届“希望杯”邀请赛试题) 如图,AB∥CD,∠EFA=30°,∠FGH=90°,∠HMN=30°,∠CNP=50°,求∠GHM的度数。
A、同一平面内不相交的两条射线是平行线。
B、同一平面内不相交的两条线是平行线。
C、同一平面内不相交的两条直线是平行线。
D、不相交的两条直线是平行线。C练习1、在正方体中,与棱AB所在直线不相交的有棱 所在的直线,其中与棱AB所在的直线平行的有棱 所在的直线。例2、阅读下面的语句,并画出符合题意的图形:(1)直线AB、CD是相交直线,点P是直线AB外一点,直线EF经过P点与与直线AB平行,与直线CD相交于E;(2)点P是直线AB外一点,直线CD经过点P,且与直线AB平行。练习2、如图,过⊿ABC的边AB的中点D,画平行于BC的直线,交AC于点E。知识点二、两直线平行的条件1、同位角、内错角、同旁内角的概念关键点提示:首先要确定这一对角是由哪两条直线被哪一条直线所截而形成的,然后再看它们的位置关系,并由此位置关系确定它们是一对什么角。2。直线平行的条件:定理1、同位角相等,两直线平行。文字形式∵∠1=∠5∴AB∥CD数学形式:图形形式: 请你用三种形式理解另两种类似的平行判定的条件。例3、如图,直线BC、DE被直线AB所截。
(1) ∠1与 ∠2, ∠1与 ∠3, ∠1与 ∠4各是一对什么角?
(2)如果 ∠1= ∠4,那么 ∠1与 ∠2相等吗? ∠1与 ∠3有什么关系?练习3、如图,与∠1是同位角的是 ,与∠1是内错角的是 ,与∠1是同旁内角的是 。例4、如图,已知m1与m2、m3相交于A、B两点,若∠1=30°,∠2=150°,试说明m2∥m3, 练习4、如图,如果∠1=47°,∠2=133°,∠D=47°,那么BC与DE平行吗?AB与CD呢?例5、如果两条直线都垂直于同一条直线,那么这两条直线平行吗?为什么?练习5、判断:
(1)∵a∥c,b∥c,∴a∥b(2) ∵a⊥c,b⊥c,∴a⊥b疑难解析 疑点:由“同位角相等,两直线平行”,你能得到“内错角相等,两直线平行”、“同旁内角互补,两直线平行” 规律:遇到一个新问题时,常常把它转化为已知的(或已经解决的)问题来解决,这是一种重要的数学思想。例6、已知,如图,BE平分∠ABC,∠1=∠3,试说明:BC∥DE疑难解析疑难解析 难点:已知几何基本图形不是我们所学过的“三线八角”基本图形,需添加一些辅助线把它转化成我们熟悉的图形。疑难解析例8、已知,如图,AB∥CD,P是AB、CD之间的一点,已知∠B=32°,∠C=25°,求∠BPC的度数。挑战自我?
(第12届“希望杯”邀请赛试题) 如图,AB∥CD,∠EFA=30°,∠FGH=90°,∠HMN=30°,∠CNP=50°,求∠GHM的度数。
