2022-2023学年华东师大版八年级数学上册 12.5因式分解 课件(共24张PPT)
文档属性
| 名称 | 2022-2023学年华东师大版八年级数学上册 12.5因式分解 课件(共24张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-09 08:30:09 | ||
图片预览



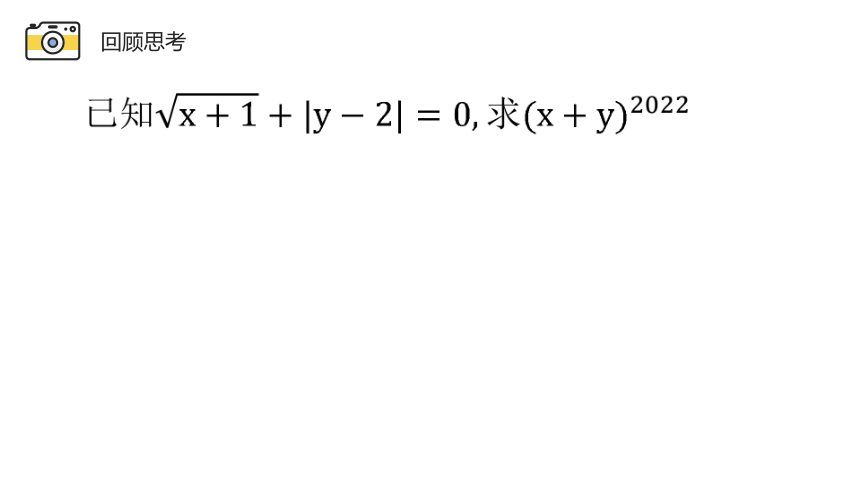
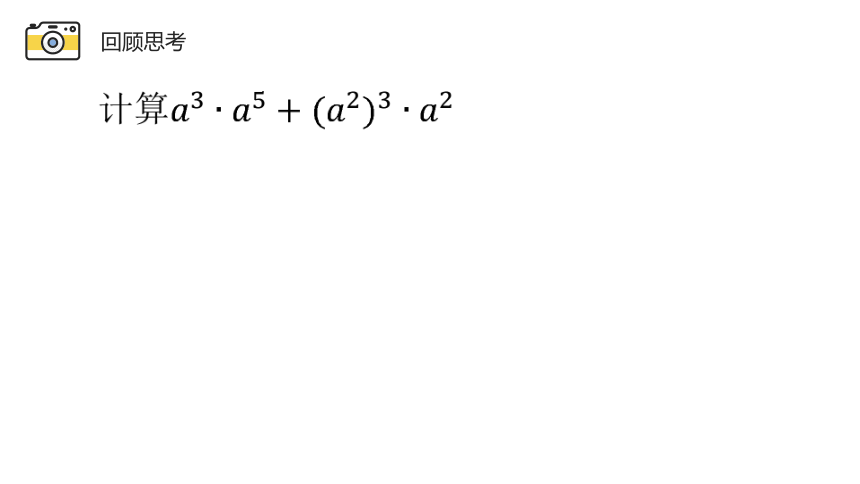
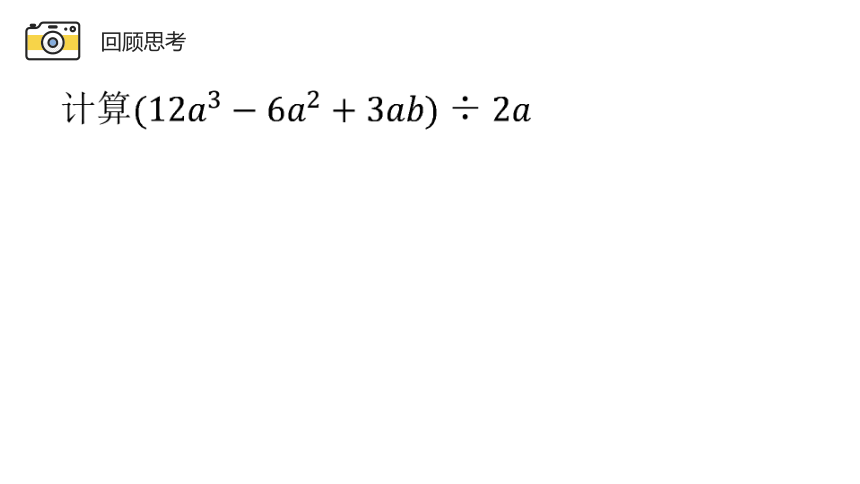


文档简介
(共24张PPT)
12.5因式分解
回顾思考
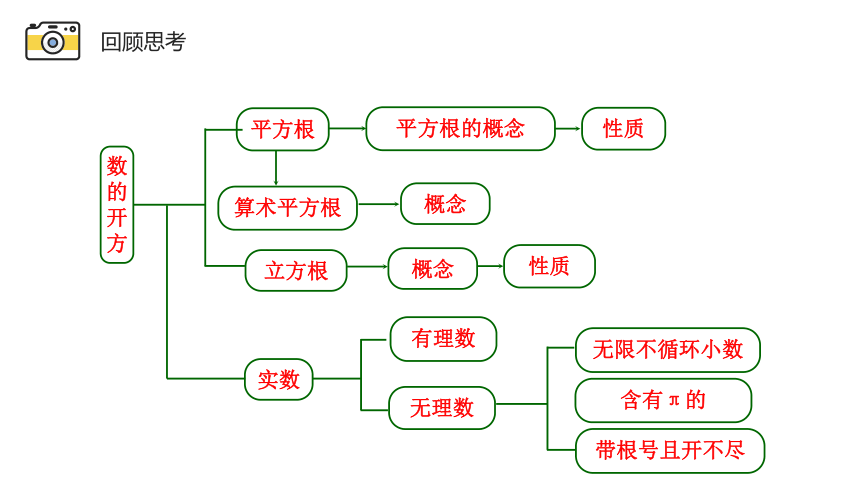
数的开方
平方根
算术平方根
立方根
实数
平方根的概念
性质
概念
概念
性质
有理数
无理数
无限不循环小数
含有π的
带根号且开不尽
回顾思考
整式的乘法
整式的除法
幂的运算
击鼓传花
老师背对同学播放班歌,同时传递物品,音乐一停,传到谁请谁来回答,答对有奖,答错无惩。
回顾思考
回顾思考
回顾思考
计算
回顾思考
运用前面所学的知识填空:
(1) m(a+b+c)= ;
(2) (a+b)(a-b)= ;
(3) (a+b)2 = .
ma+mb+mc
a2 -b2
a2 +2ab+b2
探究新知
按照前面的三个等式,填空:
(1) ma+mb+mc= ;
(2) a2 -b2= ;
(3) a2 +2ab+b2= .
m(a+b+c)
(a+b)(a-b)
(a+b)2
都是多项式化为几个整式的积的形式.
把一个多项式化为几个整式的积的形式,叫做多项式的因式分解,也叫做把这个多项式分解因式.
新知引入
因式分解
把一个多项式化为几个整式的积的形式,叫做多项式的因式分解,也叫做把这个多项式分解因式.
结果:①几个整式 ②乘积
条件:①一个多项式
探究新知
把一个多项式化为几个整式的积的形式,叫做多项式的因式分解,也叫做把这个多项式分解因式.
想一想:整式乘法与因式分解有什么关系?
x2-1 (x+1)(x-1)
因式分解
整式乘法
x2-1 = (x+1)(x-1)
等式的特征:左边是多项式,
右边是几个整式的乘积.
互为相反的变形,即
x2+x=x2(1+ )
思考
在下列等式中,从左到右的变形是因式分解的有 ,不是的,请说明原因.
①
②
③
④
⑤
⑥
③
⑥
am+bm+c=m(a+b)+c
24x2y=3x ·8xy
x2-1=(x+1)(x-1)
(2x+1)2=4x2+4x+1
2x+4y+6z=2(x+2y+3z)
最后不是积的运算
因式分解的对象是多项式,而不是单项式
是整式的乘法
每个因式必须是整式
pa+pb+pc
探究新知
多项式中各项都含有的相同因式,叫做这个多项式的公因式.
相同因式p
这个多项式有什么特点?
新知引入
公因式
多项式中各项都含有的相同因式,叫做这个多项式的公因式.
小试牛刀
例1、
找 3x 2 – 6xy 的公因式.
系数:最大公因数
3
字母:相同的字母
x
所以公因式是3x.
指数:相同字母的最低次幂
1
探究新知
1.定系数:公因式的系数是多项式各项系数的最大公因数.
2.定字母:字母取多项式各项中都含有的相同字母. 3.定指数:相同字母的指数取各项中最小的,即字母最低次幂.
找公因式3步曲
It's your turn
练习1、
下列各多项式的公因式是什么?
3
a
a2
2(m+n)
3mn
-2xy
(1) 3x+6y;
(2)ab-2ac;
(3) a2 - a3;
(4)4 (m+n) 2 +2(m+n);
(5)9m2n-6mn ;
(6)-6x 2y-8xy2.
探究新知
( a+b+c )
pa+ pb +pc
p
=
提公因式法
一般地,如果多项式的各项有公因式,可以把这个公因式提取出来,将多项式写成公因式与另一个因式的乘积的形式,这种分解因式的方法叫做提公因式法.
步骤:①找公因式(3步曲)
②提公因式,并确定另一个因式
小试牛刀
(1) 2m2-4m (2) -4a3b3+6a2b-2ab
例2、把下列多项式分解因式
如果存在与公因式相同的项,提取公因式后是“1”或“-1”
首项为负,可提取公因式-1.
提负号,注意变号
It's your turn
练习2、因式分解 (课堂讲练第17页)
(1)
(2)
(3) 8a3b2 + 12ab3c
(4) 2a(b+c) - 3(b+c)
注意:公因式既可以是一个单项式的形式,也可以是一个多项式的形式.
小结
因式分解
把一个多项式化为几个整式的积的形式,叫做多项式的因式分解,也叫做把这个多项式分解因式.
公因式
多项式中各项都含有的相同因式,叫做这个多项式的公因式.
小结
( a+b+c )
pa+ pb +pc
p
=
提公因式法
一般地,如果多项式的各项有公因式,可以把这个公因式提取出来,将多项式写成公因式与另一个因式的乘积的形式,这种分解因式的方法叫做提公因式法.
步骤:①找公因式(3步曲)
②提公因式,并确定另一个因式
当堂小测
1.把下列各式分解因式
(1) 8m2n+2mn
(2) 12xyz-9x2y2
(3) p(a2 + b2 )- q(a2 + b2 )
(4) -x3y3-x2y2-xy
+
+
(5)
下课!
12.5因式分解
回顾思考
数的开方
平方根
算术平方根
立方根
实数
平方根的概念
性质
概念
概念
性质
有理数
无理数
无限不循环小数
含有π的
带根号且开不尽
回顾思考
整式的乘法
整式的除法
幂的运算
击鼓传花
老师背对同学播放班歌,同时传递物品,音乐一停,传到谁请谁来回答,答对有奖,答错无惩。
回顾思考
回顾思考
回顾思考
计算
回顾思考
运用前面所学的知识填空:
(1) m(a+b+c)= ;
(2) (a+b)(a-b)= ;
(3) (a+b)2 = .
ma+mb+mc
a2 -b2
a2 +2ab+b2
探究新知
按照前面的三个等式,填空:
(1) ma+mb+mc= ;
(2) a2 -b2= ;
(3) a2 +2ab+b2= .
m(a+b+c)
(a+b)(a-b)
(a+b)2
都是多项式化为几个整式的积的形式.
把一个多项式化为几个整式的积的形式,叫做多项式的因式分解,也叫做把这个多项式分解因式.
新知引入
因式分解
把一个多项式化为几个整式的积的形式,叫做多项式的因式分解,也叫做把这个多项式分解因式.
结果:①几个整式 ②乘积
条件:①一个多项式
探究新知
把一个多项式化为几个整式的积的形式,叫做多项式的因式分解,也叫做把这个多项式分解因式.
想一想:整式乘法与因式分解有什么关系?
x2-1 (x+1)(x-1)
因式分解
整式乘法
x2-1 = (x+1)(x-1)
等式的特征:左边是多项式,
右边是几个整式的乘积.
互为相反的变形,即
x2+x=x2(1+ )
思考
在下列等式中,从左到右的变形是因式分解的有 ,不是的,请说明原因.
①
②
③
④
⑤
⑥
③
⑥
am+bm+c=m(a+b)+c
24x2y=3x ·8xy
x2-1=(x+1)(x-1)
(2x+1)2=4x2+4x+1
2x+4y+6z=2(x+2y+3z)
最后不是积的运算
因式分解的对象是多项式,而不是单项式
是整式的乘法
每个因式必须是整式
pa+pb+pc
探究新知
多项式中各项都含有的相同因式,叫做这个多项式的公因式.
相同因式p
这个多项式有什么特点?
新知引入
公因式
多项式中各项都含有的相同因式,叫做这个多项式的公因式.
小试牛刀
例1、
找 3x 2 – 6xy 的公因式.
系数:最大公因数
3
字母:相同的字母
x
所以公因式是3x.
指数:相同字母的最低次幂
1
探究新知
1.定系数:公因式的系数是多项式各项系数的最大公因数.
2.定字母:字母取多项式各项中都含有的相同字母. 3.定指数:相同字母的指数取各项中最小的,即字母最低次幂.
找公因式3步曲
It's your turn
练习1、
下列各多项式的公因式是什么?
3
a
a2
2(m+n)
3mn
-2xy
(1) 3x+6y;
(2)ab-2ac;
(3) a2 - a3;
(4)4 (m+n) 2 +2(m+n);
(5)9m2n-6mn ;
(6)-6x 2y-8xy2.
探究新知
( a+b+c )
pa+ pb +pc
p
=
提公因式法
一般地,如果多项式的各项有公因式,可以把这个公因式提取出来,将多项式写成公因式与另一个因式的乘积的形式,这种分解因式的方法叫做提公因式法.
步骤:①找公因式(3步曲)
②提公因式,并确定另一个因式
小试牛刀
(1) 2m2-4m (2) -4a3b3+6a2b-2ab
例2、把下列多项式分解因式
如果存在与公因式相同的项,提取公因式后是“1”或“-1”
首项为负,可提取公因式-1.
提负号,注意变号
It's your turn
练习2、因式分解 (课堂讲练第17页)
(1)
(2)
(3) 8a3b2 + 12ab3c
(4) 2a(b+c) - 3(b+c)
注意:公因式既可以是一个单项式的形式,也可以是一个多项式的形式.
小结
因式分解
把一个多项式化为几个整式的积的形式,叫做多项式的因式分解,也叫做把这个多项式分解因式.
公因式
多项式中各项都含有的相同因式,叫做这个多项式的公因式.
小结
( a+b+c )
pa+ pb +pc
p
=
提公因式法
一般地,如果多项式的各项有公因式,可以把这个公因式提取出来,将多项式写成公因式与另一个因式的乘积的形式,这种分解因式的方法叫做提公因式法.
步骤:①找公因式(3步曲)
②提公因式,并确定另一个因式
当堂小测
1.把下列各式分解因式
(1) 8m2n+2mn
(2) 12xyz-9x2y2
(3) p(a2 + b2 )- q(a2 + b2 )
(4) -x3y3-x2y2-xy
+
+
(5)
下课!
