2022_2023学年湘教版八年级数学上册2.5 全等三角形 第1课时 全等三角形的概念 课件(共30张PPT)
文档属性
| 名称 | 2022_2023学年湘教版八年级数学上册2.5 全等三角形 第1课时 全等三角形的概念 课件(共30张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 580.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-09 00:00:00 | ||
图片预览









文档简介
(共30张PPT)
第2章 三角形
2.5 全等三角形
第1课时 全等三角形的概念
1.知道什么是全等形、全等三角形及全等三角形的对应元素.
2.能熟练找出两个全等三角形的对应角、对应边,能用符号正确地表示两个三角形全等.
3.通过动手操作找到全等三角形的对应边相等、对应角相等的性质.
◎重点:全等三角形的概念和性质.
◎难点:全等三角形对应元素的确定.
同学们只要稍加留意就会发现我们身边有许许多多“一模一样”的图形,比如两张由同一底片冲印出来的完全相同的照片,用两张纸重叠在一起剪出的两张窗花等.几何中,我们把“一模一样”的图形叫作“全等形”,那么,究竟什么是“全等形”?
今天,我们一起来认识和学习“全等形”.
全等三角形的概念和对应元素
阅读课本本课时相关内容,解决下列问题.
1.明晰概念:能够完全重合的两个图形称为 全等形 ,能够完全重合的三角形称为 全等三角形 ,全等形的形状和大小都相同.
全等形
全等三角形
2.(1)观察:“图2-36”中,将一个图形进行平移、旋转、轴反射的变换,是否改变图形的形状与大小?
不改变.
(2)将一个三角形通过 平移 、 旋转 、 轴反射 的变换后,得到的图形与原图形全等.
平移
旋转
轴反射
3.全等的三角形中互相重合的顶点叫作 对应顶点 ,互相重合的边叫作 对应边 ,互相重合的角叫作 对应角 ,“全等”用数学符号表达为 ≌ ,读作 全等于 .注意:应把表示对应顶点的字母写在 对应 位置上.
对应顶点
对应边
对应角
≌
全等于
对应
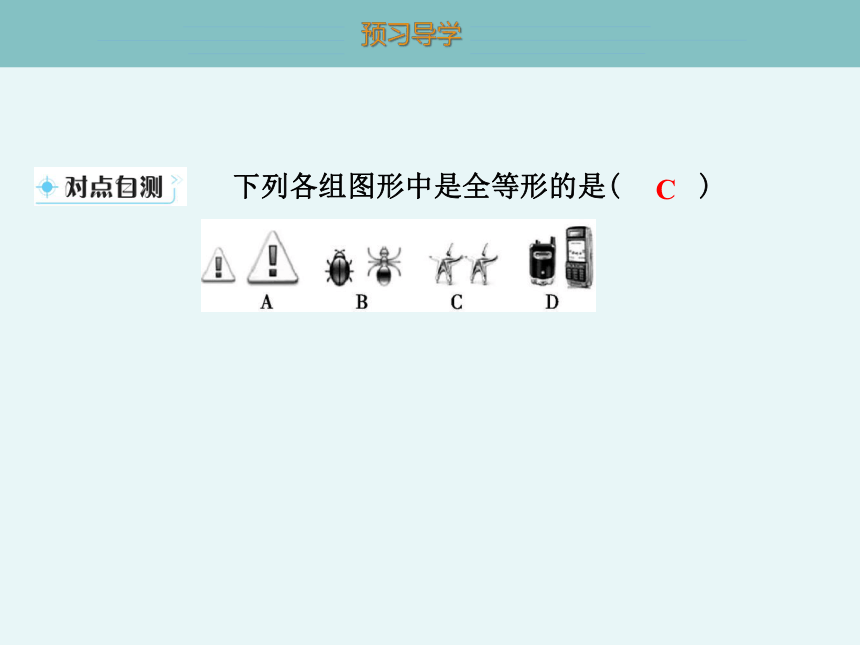
下列各组图形中是全等形的是( C )
C
全等三角形的性质
阅读课本“例1”前的一段文字,回答下列问题.
1.(1)思考:两个完全重合的角,它们相等吗?两个完全重合的线段,它们相等吗?
相等.
(2)归纳:由于两个全等三角形能完全重合,所以全等三角形的对应边 相等 ;全等三角形的对应角 相等 .用符号语言表示:
∵△ABC≌△DEF,∴AB= DE ,BC= EF ,AC= DF ;∠A= ∠D ,∠B= ∠E ,∠C= ∠F .
相等
相等
DE
EF
DF
∠D
∠E
∠F
2.讨论:全等三角形的对应边相等、对应角相等,那么它们的周长相等、面积相等.这种说法正确吗?
正确.
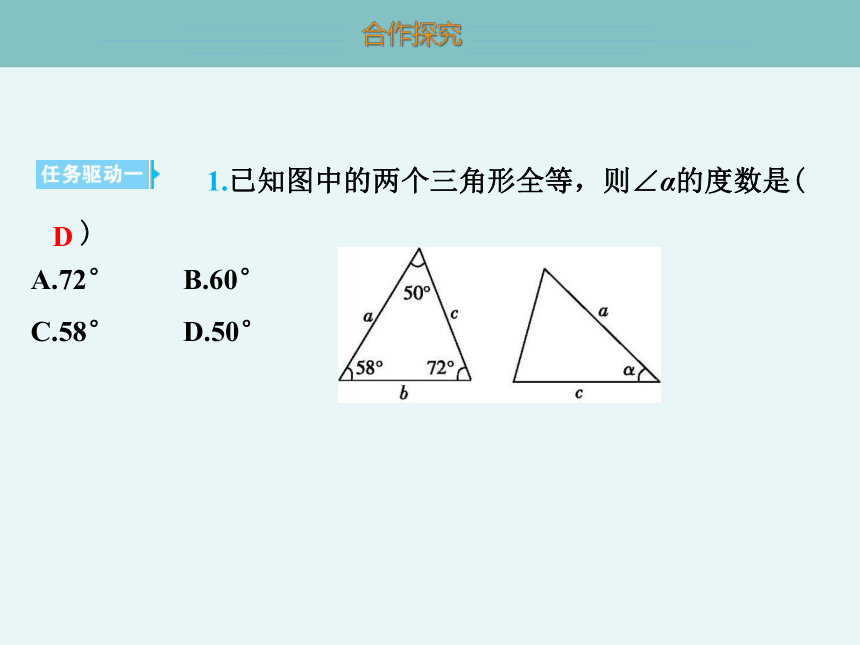
1.已知图中的两个三角形全等,则∠α的度数是( D )
A.72° B.60°
C.58° D.50°
D
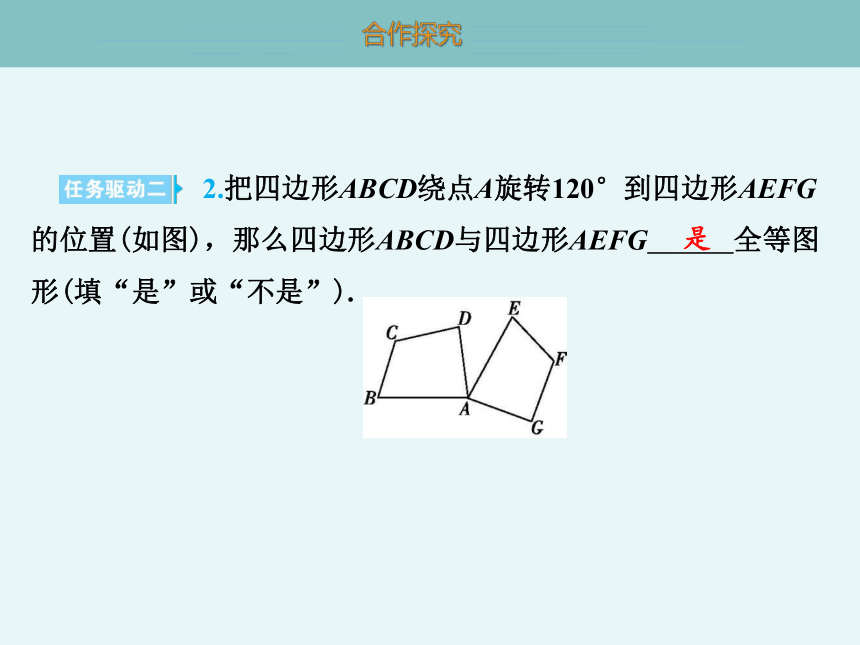
2.把四边形ABCD绕点A旋转120°到四边形AEFG的位置(如图),那么四边形ABCD与四边形AEFG 是 全等图形(填“是”或“不是”).
是
3.如图,这两个三角形全等,用符号表示为△ABC≌△DEF,你能写出对应顶点、对应边、对应角吗?
解:对应顶点:点A与点D,点B与点E,点C与点F;对应边:边AB与DE,边AC与边DF,边BC与边EF;对应角:∠A与∠D,∠B与∠E,∠ACB与∠DFE.
变式演练 “任务驱动三”中的条件不变,当∠ACB=50°时,求∠FOC的度数,你还能得到相等的角吗?请写出来,并说明理由.
解:∵△ABC≌△DEF,∴∠DFE=∠ACB=50°,∴∠FOC=180°—(∠DFE+∠ACB)=80°;
还能得到相等的角有:∠AOF=∠DOC,∠BFO=∠ECO.因为对顶角相等,所以∠AOF=∠DOC.∵△ABC≌△DEF,∴∠DFE=∠ACB.∵∠DFE=∠ACB,∴∠BFO=∠ECO.
方法归纳交流 在确定全等三角形对应边和对应角时,可以参考以下几种方法:①全等三角形对应边所对的角是 对应角 ,对应角所对的边是 对应边 ;②有公共边的,公共边一定是 对应边 ;③有公共角的,公共角一定是 对应角 ;④有对顶角的,对顶角一定是对应角;⑤两个全等三角形中一组最长的边是对应边,一组最短的边是对应边;⑥两个全等三角形中一组最大的角是对应角,一组最小的角是对应角.
对应角
对应边
对应边
对应角
(学法指导:可以先确定线段BC和EF之间的关系)4.如图,B、F、C、E在同一条直线上,△ABC≌△DEF,线段BF与线段EC有什么关系?说说你的理由.
解:BF=EC.∵△ABC≌△DEF,∴EF=BC.∴EF-CF=BC-CF.
即BF=EC.
变式演练 “任务驱动四”中的条件不变,如果有BC=5 cm,CE=2 cm,∠B=45°,∠ACB=30°,你能求出线段FC的长度和∠D的度数吗?
解:∵BC=5 cm,∴EF=5 cm.∵CE=2 cm,∴FC=EF-CE=5-2=3 cm.∵∠B=45°,∠ACB=30°,∴∠A=180°-∠B-∠ACB=180°-45°-30°=105°.∴∠D=105°.
1.如图,四边形ABCD与四边形A'B'C'D'全等,则∠A'= 120 °,∠A= 70 °,B'C'= 10 ,AD= 6 .
120
70
10
6
2.如图,已知CD⊥AB于D,BE⊥AC于E,△ABE≌△ACD,∠C=20°,AB=10,AD=4,G为AB延长线上一点.求∠EBG的度数和CE的长.
解:利用全等三角形的对应角相等性质及外角或邻补角的知识,求得∠EBG等于160°.利用全等三角形对应边相等的性质及等量减等量差相等的关系可得:CE=CA-AE=BA-AD=6.
1下列各组图形中是全等图形的是 ( B )
A B C D
B
AC和DC
∠1和∠2、∠3和∠4、∠A和
∠D
2如图,把△ABC沿直线BC翻折180°,得△ABC≌△DBC,对应边分别为 AB和DB 、 BC和BC 、 AC和DC ,对应角分别为 ∠1和∠2、∠3和∠4、∠A和∠D .
AB和DB
BC和BC
3如图,△ABE≌△ACD,∠B=50°,∠AEC=120°,则∠DAC的度数是 ( B )
B
A.120°
B.70°
C.60°
D.50°
4如图,△ACB≌△AED,AC与AE是对应边,∠B与∠D是对应角,请写出其他的对应边和对应角.
解:其他对应边:BC与DE,AB与AD;
其他对应角:∠C与∠E,∠CAB与∠EAD.
5如图,△ABC≌△EFD,图中BC和FD相等吗?说说你的理由.
解:相等,因为△ABC≌△EFD,由全等三角形对应边相等得BC=FD.
6下列各组图形中不是全等图形的一组是 ( B )
B
7下列命题中不正确的是 ( D )
A.全等三角形的对应角相等
B.全等三角形的面积相等
C.全等三角形的周长相等
D.周长相等的两个三角形全等
8如图,△ABC≌△DEF,BE=4,AE=1,则DE= 5 .
D
5
9如图,△ABC≌△DCB,AB和DC是对应边,指出其他的对应边和对应角.
解:AC和DB、BC和CB分别是对应边;∠A和∠D、∠ABC和∠DCB、∠ACB和∠DBC分别是对应角.
10如图,在正方形ABCD中,E是正方形边AD上一点,F是BA延长线上一点,并且AF=AE.
(1)可以通过平移、翻折、旋转中的哪一种方法,使△ABE与△ADF完全重合?
(2)指出图中线段BE与DF之间的关系,并证明.
解:(1)△ABE绕点A逆时针旋转90°后与△ADF重合.
(2)线段BE与DF之间的关系为BE=DF,且BE⊥DF,
∵△ABE≌△ADF,∴BE=DF,∠ADF=∠ABE.
又∵在Rt△ADF中,∠ADF+∠AFD=90°,
∴∠ABE+∠DFA=90°.∴可得到BE⊥DF.
第2章 三角形
2.5 全等三角形
第1课时 全等三角形的概念
1.知道什么是全等形、全等三角形及全等三角形的对应元素.
2.能熟练找出两个全等三角形的对应角、对应边,能用符号正确地表示两个三角形全等.
3.通过动手操作找到全等三角形的对应边相等、对应角相等的性质.
◎重点:全等三角形的概念和性质.
◎难点:全等三角形对应元素的确定.
同学们只要稍加留意就会发现我们身边有许许多多“一模一样”的图形,比如两张由同一底片冲印出来的完全相同的照片,用两张纸重叠在一起剪出的两张窗花等.几何中,我们把“一模一样”的图形叫作“全等形”,那么,究竟什么是“全等形”?
今天,我们一起来认识和学习“全等形”.
全等三角形的概念和对应元素
阅读课本本课时相关内容,解决下列问题.
1.明晰概念:能够完全重合的两个图形称为 全等形 ,能够完全重合的三角形称为 全等三角形 ,全等形的形状和大小都相同.
全等形
全等三角形
2.(1)观察:“图2-36”中,将一个图形进行平移、旋转、轴反射的变换,是否改变图形的形状与大小?
不改变.
(2)将一个三角形通过 平移 、 旋转 、 轴反射 的变换后,得到的图形与原图形全等.
平移
旋转
轴反射
3.全等的三角形中互相重合的顶点叫作 对应顶点 ,互相重合的边叫作 对应边 ,互相重合的角叫作 对应角 ,“全等”用数学符号表达为 ≌ ,读作 全等于 .注意:应把表示对应顶点的字母写在 对应 位置上.
对应顶点
对应边
对应角
≌
全等于
对应
下列各组图形中是全等形的是( C )
C
全等三角形的性质
阅读课本“例1”前的一段文字,回答下列问题.
1.(1)思考:两个完全重合的角,它们相等吗?两个完全重合的线段,它们相等吗?
相等.
(2)归纳:由于两个全等三角形能完全重合,所以全等三角形的对应边 相等 ;全等三角形的对应角 相等 .用符号语言表示:
∵△ABC≌△DEF,∴AB= DE ,BC= EF ,AC= DF ;∠A= ∠D ,∠B= ∠E ,∠C= ∠F .
相等
相等
DE
EF
DF
∠D
∠E
∠F
2.讨论:全等三角形的对应边相等、对应角相等,那么它们的周长相等、面积相等.这种说法正确吗?
正确.
1.已知图中的两个三角形全等,则∠α的度数是( D )
A.72° B.60°
C.58° D.50°
D
2.把四边形ABCD绕点A旋转120°到四边形AEFG的位置(如图),那么四边形ABCD与四边形AEFG 是 全等图形(填“是”或“不是”).
是
3.如图,这两个三角形全等,用符号表示为△ABC≌△DEF,你能写出对应顶点、对应边、对应角吗?
解:对应顶点:点A与点D,点B与点E,点C与点F;对应边:边AB与DE,边AC与边DF,边BC与边EF;对应角:∠A与∠D,∠B与∠E,∠ACB与∠DFE.
变式演练 “任务驱动三”中的条件不变,当∠ACB=50°时,求∠FOC的度数,你还能得到相等的角吗?请写出来,并说明理由.
解:∵△ABC≌△DEF,∴∠DFE=∠ACB=50°,∴∠FOC=180°—(∠DFE+∠ACB)=80°;
还能得到相等的角有:∠AOF=∠DOC,∠BFO=∠ECO.因为对顶角相等,所以∠AOF=∠DOC.∵△ABC≌△DEF,∴∠DFE=∠ACB.∵∠DFE=∠ACB,∴∠BFO=∠ECO.
方法归纳交流 在确定全等三角形对应边和对应角时,可以参考以下几种方法:①全等三角形对应边所对的角是 对应角 ,对应角所对的边是 对应边 ;②有公共边的,公共边一定是 对应边 ;③有公共角的,公共角一定是 对应角 ;④有对顶角的,对顶角一定是对应角;⑤两个全等三角形中一组最长的边是对应边,一组最短的边是对应边;⑥两个全等三角形中一组最大的角是对应角,一组最小的角是对应角.
对应角
对应边
对应边
对应角
(学法指导:可以先确定线段BC和EF之间的关系)4.如图,B、F、C、E在同一条直线上,△ABC≌△DEF,线段BF与线段EC有什么关系?说说你的理由.
解:BF=EC.∵△ABC≌△DEF,∴EF=BC.∴EF-CF=BC-CF.
即BF=EC.
变式演练 “任务驱动四”中的条件不变,如果有BC=5 cm,CE=2 cm,∠B=45°,∠ACB=30°,你能求出线段FC的长度和∠D的度数吗?
解:∵BC=5 cm,∴EF=5 cm.∵CE=2 cm,∴FC=EF-CE=5-2=3 cm.∵∠B=45°,∠ACB=30°,∴∠A=180°-∠B-∠ACB=180°-45°-30°=105°.∴∠D=105°.
1.如图,四边形ABCD与四边形A'B'C'D'全等,则∠A'= 120 °,∠A= 70 °,B'C'= 10 ,AD= 6 .
120
70
10
6
2.如图,已知CD⊥AB于D,BE⊥AC于E,△ABE≌△ACD,∠C=20°,AB=10,AD=4,G为AB延长线上一点.求∠EBG的度数和CE的长.
解:利用全等三角形的对应角相等性质及外角或邻补角的知识,求得∠EBG等于160°.利用全等三角形对应边相等的性质及等量减等量差相等的关系可得:CE=CA-AE=BA-AD=6.
1下列各组图形中是全等图形的是 ( B )
A B C D
B
AC和DC
∠1和∠2、∠3和∠4、∠A和
∠D
2如图,把△ABC沿直线BC翻折180°,得△ABC≌△DBC,对应边分别为 AB和DB 、 BC和BC 、 AC和DC ,对应角分别为 ∠1和∠2、∠3和∠4、∠A和∠D .
AB和DB
BC和BC
3如图,△ABE≌△ACD,∠B=50°,∠AEC=120°,则∠DAC的度数是 ( B )
B
A.120°
B.70°
C.60°
D.50°
4如图,△ACB≌△AED,AC与AE是对应边,∠B与∠D是对应角,请写出其他的对应边和对应角.
解:其他对应边:BC与DE,AB与AD;
其他对应角:∠C与∠E,∠CAB与∠EAD.
5如图,△ABC≌△EFD,图中BC和FD相等吗?说说你的理由.
解:相等,因为△ABC≌△EFD,由全等三角形对应边相等得BC=FD.
6下列各组图形中不是全等图形的一组是 ( B )
B
7下列命题中不正确的是 ( D )
A.全等三角形的对应角相等
B.全等三角形的面积相等
C.全等三角形的周长相等
D.周长相等的两个三角形全等
8如图,△ABC≌△DEF,BE=4,AE=1,则DE= 5 .
D
5
9如图,△ABC≌△DCB,AB和DC是对应边,指出其他的对应边和对应角.
解:AC和DB、BC和CB分别是对应边;∠A和∠D、∠ABC和∠DCB、∠ACB和∠DBC分别是对应角.
10如图,在正方形ABCD中,E是正方形边AD上一点,F是BA延长线上一点,并且AF=AE.
(1)可以通过平移、翻折、旋转中的哪一种方法,使△ABE与△ADF完全重合?
(2)指出图中线段BE与DF之间的关系,并证明.
解:(1)△ABE绕点A逆时针旋转90°后与△ADF重合.
(2)线段BE与DF之间的关系为BE=DF,且BE⊥DF,
∵△ABE≌△ADF,∴BE=DF,∠ADF=∠ABE.
又∵在Rt△ADF中,∠ADF+∠AFD=90°,
∴∠ABE+∠DFA=90°.∴可得到BE⊥DF.
同课章节目录
