比例性质和平行线分线段成比例定理[下学期]
文档属性
| 名称 | 比例性质和平行线分线段成比例定理[下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 347.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-11-17 00:00:00 | ||
图片预览






文档简介
课件19张PPT。精品
中考复习方案
数学分册
比例性质和平行线分线段 成比例定理要点、考点聚焦
课前热身
典型例题解析
课时训练要点、考点聚焦一、本课时的重点
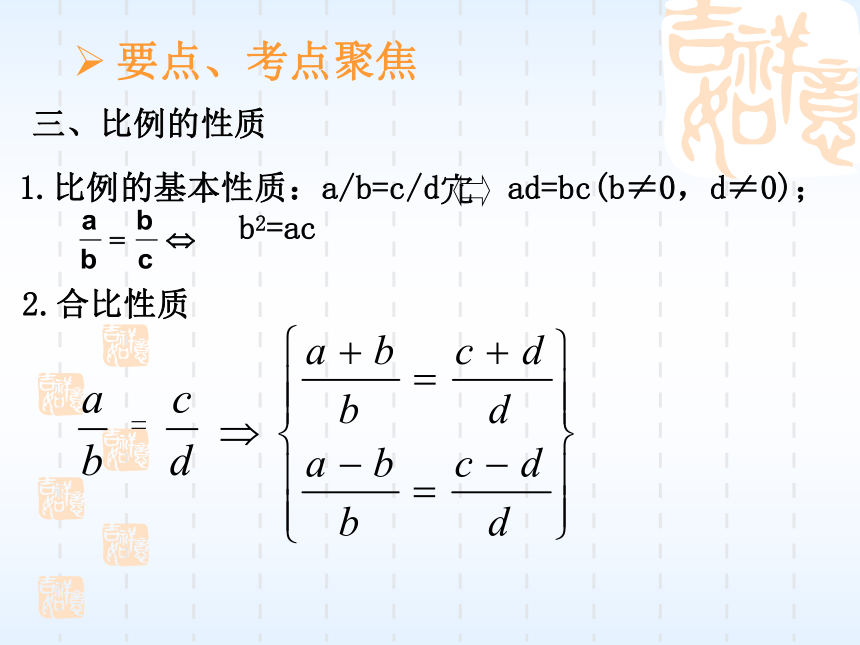
比例性质和平行线分线段成比例定理.二、比例线段 3.比例中项:若a/b=c/d=bc,则b叫a、c的比例
中项.1.比例线段:在四条线段中,如果其中两条线段的比等于另外两条线段的比,那么这四条线段叫做成比例线段,简称比例线段.2.第四比例项:若a/b=c/d,则d叫a、b、c的第四比例项.三、比例的性质 1.比例的基本性质:a/b=c/d? ad=bc(b≠0,d≠0);
b2=ac=2.合比性质 要点、考点聚焦3. 等比性质:若 = =…= (b+d+…+n≠0),那么. 四、平行线分线段成比例定理及推论定理:三条平行线截两条直线,所得的对应线段成比例.
推论:平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例.
推论的逆定理:如果一条直线截三角形的两边(或两边的延长线)所得的对应线段成比例,那么这条直线平行于三角形的第三边. 五、中考要求 (1)会利用比例性质求比例中项、第四比例项
及代数式的值. (2)会求比例尺. (3)能灵活运用平行线分线段成比例定理及推论
证明线段成比例,并会利用推论的逆定理证明
两直线平行.
课前热身1.比例尺是1∶38000的南京交通游
览图上,玄武湖隧道长约7cm它的实际长度约为 ( )
A.0.266km B.2.66km
C.26.6km D.266km 2.设2a-3b=0,则 = , =3.若4是x和 的比例中项,则x= B4.如图所示,DE∥BC,EF∥AB,现得到下列结论:其中正确的比例式的个数是( )
A.4个 B.3个
C. 2个 D.1个 B图6-1-2DE
DM典型例题解析【解析】方法1:设x=2k,y=3k,z=4k,代入求值,这种方法比较适用,故选C. 方法2:利用比例的性质, C【解析】这是一道开放型考题,旨在考查学生的发散思维
能力,由于题中没有明确这四个数的顺序,因此所添的数有很大的灵活性,根据比例的基本性质:设这个数
为x则有
典型例题解析【例3】如图6-1-3所示,有两棵树,一棵高8米,另一棵高2米,两树相距8米,一只小鸟从一棵树的树梢飞到另一棵树的树梢,至少飞了 米. 图6-1-3 典型例题解析2.掌握平行线分线段成比例定理的两种基本图形,会在较复杂的比例式中,找出恰当的过渡比.1.分清比例的性质和分式的性质.方法小结:课时训练1.如图,在菱形ABCD中,E是AB的中点,作EF//BC交AC于点F。如果EF=4,那么CD的长为( )
A.2 B.4
C.6 D.8 2.(2004·陕西省)如图,在平行
四边形ABCD中,AB=4cm,AD=
7cm,∠ABC的平分线交AD于点E,
交CD的延长线于点F,则DF=
cm.D33.在同一时刻的阳光下,小明的影子比小强的影子长,那么在同一路灯光下 ( )
A.小明的影子比小强的影子长
B.小明的影子比小强的影子短
C.小明的影子和小强的影子一样长
D.无法判断谁的影子长 D课时训练课时训练4.如图,在梯形ABCD中,AD//BC,
E、F分别是AB、CD的中点,EF
分别交BD、AC于G、H,设
BC-AD=m,则GH的长为 ( )
A.2m B.m
C.2m/3 D.m/2 D5.如图,在平行四边形ABCD中,AE:EB=1:2,BF//DE,SΔAGE=6cm2,则四边形FDGH的面积为 ( )
A.48cm2 B.24cm2
C.18cm2 D.12cm2 A6.已知线段a=4cm,b=9cm,则线段a、b的比例中项
c= cm. 7.如图所示,在平行四边形ABCD中,E是BC上一点,BE∶EC=2∶3,AE交BD于点F,则BF∶FD= . 2:56课时训练再见!
中考复习方案
数学分册
比例性质和平行线分线段 成比例定理要点、考点聚焦
课前热身
典型例题解析
课时训练要点、考点聚焦一、本课时的重点
比例性质和平行线分线段成比例定理.二、比例线段 3.比例中项:若a/b=c/d=bc,则b叫a、c的比例
中项.1.比例线段:在四条线段中,如果其中两条线段的比等于另外两条线段的比,那么这四条线段叫做成比例线段,简称比例线段.2.第四比例项:若a/b=c/d,则d叫a、b、c的第四比例项.三、比例的性质 1.比例的基本性质:a/b=c/d? ad=bc(b≠0,d≠0);
b2=ac=2.合比性质 要点、考点聚焦3. 等比性质:若 = =…= (b+d+…+n≠0),那么. 四、平行线分线段成比例定理及推论定理:三条平行线截两条直线,所得的对应线段成比例.
推论:平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例.
推论的逆定理:如果一条直线截三角形的两边(或两边的延长线)所得的对应线段成比例,那么这条直线平行于三角形的第三边. 五、中考要求 (1)会利用比例性质求比例中项、第四比例项
及代数式的值. (2)会求比例尺. (3)能灵活运用平行线分线段成比例定理及推论
证明线段成比例,并会利用推论的逆定理证明
两直线平行.
课前热身1.比例尺是1∶38000的南京交通游
览图上,玄武湖隧道长约7cm它的实际长度约为 ( )
A.0.266km B.2.66km
C.26.6km D.266km 2.设2a-3b=0,则 = , =3.若4是x和 的比例中项,则x= B4.如图所示,DE∥BC,EF∥AB,现得到下列结论:其中正确的比例式的个数是( )
A.4个 B.3个
C. 2个 D.1个 B图6-1-2DE
DM典型例题解析【解析】方法1:设x=2k,y=3k,z=4k,代入求值,这种方法比较适用,故选C. 方法2:利用比例的性质, C【解析】这是一道开放型考题,旨在考查学生的发散思维
能力,由于题中没有明确这四个数的顺序,因此所添的数有很大的灵活性,根据比例的基本性质:设这个数
为x则有
典型例题解析【例3】如图6-1-3所示,有两棵树,一棵高8米,另一棵高2米,两树相距8米,一只小鸟从一棵树的树梢飞到另一棵树的树梢,至少飞了 米. 图6-1-3 典型例题解析2.掌握平行线分线段成比例定理的两种基本图形,会在较复杂的比例式中,找出恰当的过渡比.1.分清比例的性质和分式的性质.方法小结:课时训练1.如图,在菱形ABCD中,E是AB的中点,作EF//BC交AC于点F。如果EF=4,那么CD的长为( )
A.2 B.4
C.6 D.8 2.(2004·陕西省)如图,在平行
四边形ABCD中,AB=4cm,AD=
7cm,∠ABC的平分线交AD于点E,
交CD的延长线于点F,则DF=
cm.D33.在同一时刻的阳光下,小明的影子比小强的影子长,那么在同一路灯光下 ( )
A.小明的影子比小强的影子长
B.小明的影子比小强的影子短
C.小明的影子和小强的影子一样长
D.无法判断谁的影子长 D课时训练课时训练4.如图,在梯形ABCD中,AD//BC,
E、F分别是AB、CD的中点,EF
分别交BD、AC于G、H,设
BC-AD=m,则GH的长为 ( )
A.2m B.m
C.2m/3 D.m/2 D5.如图,在平行四边形ABCD中,AE:EB=1:2,BF//DE,SΔAGE=6cm2,则四边形FDGH的面积为 ( )
A.48cm2 B.24cm2
C.18cm2 D.12cm2 A6.已知线段a=4cm,b=9cm,则线段a、b的比例中项
c= cm. 7.如图所示,在平行四边形ABCD中,E是BC上一点,BE∶EC=2∶3,AE交BD于点F,则BF∶FD= . 2:56课时训练再见!
