人教版八年级数学上册12.1全等三角形 精选练习 (含解析)
文档属性
| 名称 | 人教版八年级数学上册12.1全等三角形 精选练习 (含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 291.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-09 08:36:20 | ||
图片预览

文档简介
12.1 全等三角形精选练习(含答案)-人教版八年级上册
一.选择题
.如图,若△ABD≌△EBC,且AB=3,BC=7,则DE的长为( )
A.2 B.4 C.10 D.3
.已知,图中的两个三角形全等,则∠α等于( )
A.80° B.70° C.60° D.50°
.如图是两个全等三角形,图中的字母表示三角形的边长,则∠1的度数是( )
A.54° B.56° C.60° D.66°
.如图,在△ABC中,AD⊥BC于点D,BE⊥AC于点E,AD,BE交于点F,△ADC
≌△BDF,若BD=4,CD=2,则△ABC的面积为( )
A.24 B.18 C.12 D.8
.如图,在四边形ABCD与四边形A'B'C'D'中,AB=A'B',∠B=∠B',BC=B'C'.下列条件中:①∠A=∠A',AD=A'D';②∠A=∠A',CD=C'D';③∠A=∠A',∠D=∠D';④AD=A'D',CD=C'D'.添加上述条件中的其中一个,可使四边形ABCD≌四边形A'B'C'D'.上述条件中符合要求的有( )
A.①②③ B.①③④ C.①④ D.①②③④
.如图,已知△ABC≌△DEF,CD平分∠BCA,若∠A=22°,∠CGF=88°,则∠E的度数是( )
A.26° B.28° C.30° D.34°
.如图,在△ABC中,ED⊥BC,EA⊥AB,若△EAB≌△EDB≌△EDC,则∠C=( )
A.36° B.30° C.25° D.15°
.两个全等的直角三角形重叠在一起.将其中的一个三角形沿着点B到C的方向平移到△DEF的位置,AB=4,DO=1,平移距离为2.则阴影部分面积为( )
A.7 B.6 C.14 D.4
.如图,N,C,A三点在同一直线上,在△ABC中,∠A:∠ABC:∠ACB=3:5:10,又△MNC≌△ABC,则∠BCM的度数等于( )
A.10° B.20° C.30° D.40°
.如图,锐角△ABC中,D、E分别是AB、AC边上的点,△ADC≌△ADC′,△AEB≌△AEB′,且C′D∥EB′∥BC,BE、CD交于点F.若∠BAC=35°,则∠BFC的大小是( )
A.105° B.110° C.100° D.120°
二.填空题
.如图,D在BC边上,△ABC≌△ADE,∠EAC=40°,则∠B的度数为 .
.如图,点E是CD上的一点,Rt△ACD≌Rt△EBC,则下结论:
①AC=BC,②AD∥BE,③∠ACB=90°,④AD+DE=BE,
成立的有 个.
.如图,在平面直角坐标系中,△OAB的顶点坐标分别是A(﹣6,0),B(0,4),△OA′B′≌△OAB,若点A′在x轴上,则点B′的坐标是 .
.如图,在2×2的方格纸中,∠1+∠2等于 .
.若△ABC≌△DEF,AB=DE=4,△DEF面积为10,则在△ABC中AB边上的高为 .
解答题
.如图,已知△ABC≌△DEF,∠A=85°,∠B=60°,AB=8,EH=2.
(1)求角F的度数与DH的长;
(2)求证:AB∥DE.
.如图,△ABC≌△DEB,点E在边AB上,DE与AC相交于点F.若DE=9,BC=4,∠D=25°,∠C=70°.
(1)求线段AE的长;
(2)求∠DBC的度数.
.已知:如图,点E在线段BC上,且△ABC≌△AED.
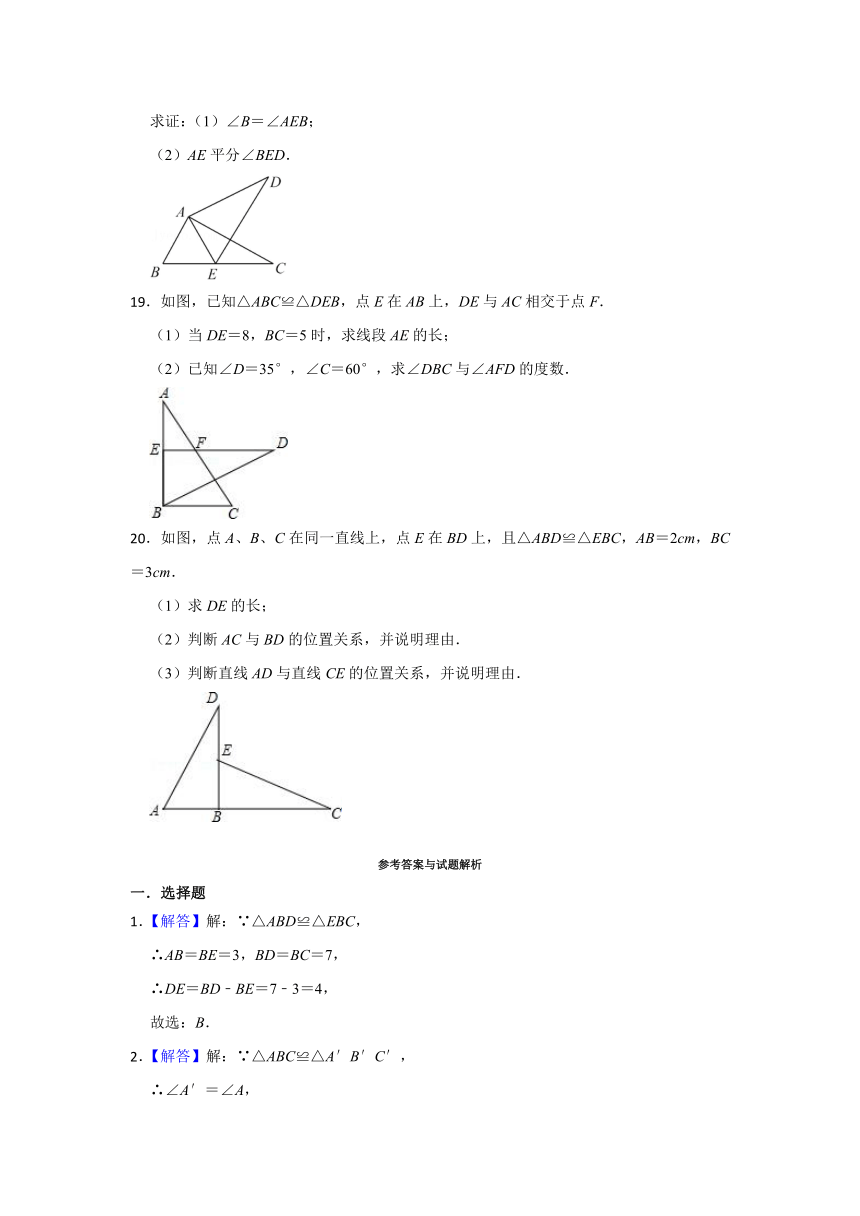
求证:(1)∠B=∠AEB;
(2)AE平分∠BED.
.如图,已知△ABC≌△DEB,点E在AB上,DE与AC相交于点F.
(1)当DE=8,BC=5时,求线段AE的长;
(2)已知∠D=35°,∠C=60°,求∠DBC与∠AFD的度数.
.如图,点A、B、C在同一直线上,点E在BD上,且△ABD≌△EBC,AB=2cm,BC=3cm.
(1)求DE的长;
(2)判断AC与BD的位置关系,并说明理由.
(3)判断直线AD与直线CE的位置关系,并说明理由.
参考答案与试题解析
一.选择题
.【解答】解:∵△ABD≌△EBC,
∴AB=BE=3,BD=BC=7,
∴DE=BD﹣BE=7﹣3=4,
故选:B.
.【解答】解:∵△ABC≌△A′B′C′,
∴∠A′=∠A,
∵∠A=180°﹣∠B﹣∠C=180°﹣60°﹣50°=70°,
∴∠A′=70°,
故选:B.
.【解答】解:
∵△ABC≌△DEF,
∴∠F=∠C=∠1,
∵∠A=54°,∠B=60°,
∴∠1=∠C=180°﹣∠A﹣∠B=180°﹣54°﹣60°=66°,
故选:D.
.【解答】解:∵△ADC≌△BDF,
∴AD=BD,
∵BD=4,
∴AD=4,
∵DC=2,
∴BC=BD+DC=4+2=6,
∴S△ABC===12,
故选:C.
.【解答】解:符合要求的条件是①③④,
证明:连接AC、A′C′,
在△ABC与△A′B′C′中,
,
∴△ABC≌△A′B′C′(SAS),
∴AC=A′C′,∠ACB=∠A′C′B′,∠ACB=∠A′C′B′,
∵∠BAD=∠B′A′D′,
∴∠BAD﹣∠DAC=∠B′A′D′﹣∠D′A′C′,
∴∠DAC=∠D′A′C′,
在△ACD和△A′C′D中,
,
∴△ACD≌△A′C′D′(SAS),
∴∠D=∠D′,∠ACD=∠A′C′D′,CD=C′D′,
∴∠BCD=∠B′C′D′,
∴四边形ABCD和四边形A′B′C′D′中,
AB=A′B′,BC=B′C′,AD=A′D′,DC=D′C′,
∠B=∠B′,∠BCD=∠B′C′D′,∠D=∠D′,∠BAD=∠B′A′D′,
∴四边形ABCD≌四边形A′B′C′D′.
同理根据③④的条件证得四边形ABCD≌四边形A′B′C′D′.
故选:B.
.【解答】解:∵△ABC≌△DEF,∠A=22°,
∴∠D=∠A=22°,∠B=∠E,
∴∠E+∠F=180°﹣∠D=180°﹣22°=158°,
在四边形ECGF中,∠ECG=360°﹣∠CGF﹣(∠E+∠F)=360°﹣88°﹣158°=114°,
∴∠DCB=180°﹣∠ECG=180°﹣114°=66°,
∵CD平分∠BCA,
∴∠BCA=2∠DCB=132°,
∴∠E=∠B=180°﹣∠A﹣∠BCA=180°﹣22°﹣132°=26°,
故选:A.
.【解答】解:∵EA⊥AB,
∴∠A=90°,
∵△EAB≌△EDB≌△EDC,
∴∠C=∠EBD,∠ABE=∠EBD,
∴∠C=∠ABE=∠EBD,
∵∠ABC+∠C=90°,
∴3∠C=90°,
∴∠C=30°,
故选:B.
.【解答】解:由平移的性质可知,△ABC≌△DEF,
∴DE=AB=4,BE=2,S△ABC=S△DEF,
∴OE=DE﹣DO=4﹣1=3,
∴阴影部分的面积=S△ABC﹣S△OEC=S梯形ABEO=×(4+3)×2=7,
故选:A.
.【解答】解:∵在△ABC中,∠A:∠ABC:∠ACB=3:5:10,∠A+∠ABC+∠ACB=180°,
∴∠A=30°,∠BCA=100°,∠ABC=50°,
∵△MNC≌△ABC,
∴∠NCM=∠ACB=100°,∠N=∠ABC=50°,BC=NC,
∴∠NBC=∠N=50°,
∴∠BCN=180°﹣∠N﹣∠NBC=80°,
∴∠BCM=∠ACB﹣∠BCN=100°﹣80°=20°,
故选:B.
.【解答】解:设∠C′=α,∠B′=β,
∵△ADC≌△ADC′,△AEB≌△AEB′,
∴∠ACD=∠C′=α,∠ABE=∠B′=β,∠BAE=∠B′AE=35°,
∴∠C′DB=∠BAC′+AC′D=35°+α,∠CEB′=35°+β.
∵C′D∥EB′∥BC,
∴∠ABC=∠C′DB=35°+α,∠ACB=∠CEB′=35°+β,
∴∠BAC+∠ABC+∠ACB=180°,即105°+α+β=180°.
则α+β=75°.
∵∠BFC=∠BDC+∠DBE,
∴∠BFC=35°+α+β=35°+75°=110°.
故选:B.
二.填空题
.【解答】解:∵△ABC≌△ADE,
∴AB=AD,∠BAC=∠DAE,
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,
∴∠BAD=∠EAC,
∵∠EAC=40°,
∴∠BAD=40°,
∵AB=AD,
∴∠B=∠ADB=(180°﹣∠BAD)=70°,
故答案为:70°.
.【解答】解:
∵Rt△ACD≌Rt△EBC,
∴AC=BE,
∵在Rt△BEC中,BE<BC,
∴AC<BC,∴①错误;
∵∠CAD=∠CEB=∠BED=90°,∠D<∠CAD,
∴∠D≠∠BED,
∴AD和BE不平行,∴②错误;
∵Rt△ACD≌Rt△EBC,
∴∠ACD=∠CEE,∠D=∠BCE,
∵∠CAD=90°,
∴∠ACD+∠D=90°,
∴∠ACB=∠ACD+∠BDE=90°,∴③正确;
∵Rt△ACD≌Rt△EBC,
∴AD=CE,CD=BC,
CD=CE+DE=AD+DE=BC,
∵BE<BC,
∴AD+DE>BE,∴④错误;
故答案为:1.
.【解答】解:∵A(﹣6,0),B(0,4),△OA′B′≌△AOB,
∴OA=OA′=6,OB=A′B′=4,
∴点B′的坐标是(6,﹣4),
故答案为:(6,﹣4).
.【解答】解:如图,在△ABC和△DEA中,
,
∴△ABC≌△DEA(SAS),
∴∠2=∠3,
在Rt△ABC中,∠1+∠3=90°,
∴∠1+∠2=90°,
故答案为:90°.
.【解答】解:设△ABC的边AB上的高为h,
∵△ABC≌△DEF,△DEF面积为10,
∴△BAC的面积是10,
∵AB=4,
∴h=10,
解得:h=5,
即△ABC中AB边上的高为5,
故答案为:5.
三.解答题
.【解答】解:(1)∵∠A=85°,∠B=60°,
∴∠ACB=180°﹣∠A﹣∠B=35°,
∵△ABC≌△DEF,AB=8,
∴∠F=∠ACB=35°,DE=AB=8,
∵EH=2,
∴DH=8﹣2=6;
(2)证明:∵△ABC≌△DEF,
∴∠DEF=∠B,
∴AB∥DE.
.【解答】解:(1)∵△ABC≌△DEB,BC=4,DE=9,
∴AB=DE=9,BE=BC=4,
∴AE=AB﹣BE=9﹣4=5;
(2)∵△ABC≌△DEB,∠D=25°,∠C=70°,
∴∠DBA=∠C=70°,∠A=∠D=25°,
∴∠ABC=180°﹣∠C﹣∠A=180°﹣70°﹣25°=85°,
∴∠DBC=∠ABC﹣∠DBA=85°﹣70°=15°.
.【解答】证明:(1)∵△ABC≌△AED,
∴AB=AE,
∴∠B=∠AEB;
(2)∵△ABC≌△AED,
∴∠B=∠AED,
又∠B=∠AEB,
∴∠AED=∠AEB,
∴AE平分∠BED.
.【解答】解:(1)∵△ABC≌△DEB,DE=8,BC=5,
∴AB=DE=8,BE=BC=5,
∴AE=AB=BE=8﹣5=3;
(2)∵△ABC≌△DEB,∠D=35°,∠C=60°,
∴∠DBE=∠C=60°,∠A=∠D=35°,∠ABC=∠DEB,
∴∠ABC=180°﹣∠A﹣∠C=85°,
∴∠DBC=∠ABC﹣∠DBE=85°﹣60°=25°,
∵∠ABC=85°,
∴∠DEB=85°,
∴∠AED=95°,
∴∠AFD=∠A+∠AED=35°+95°=130°.
.【解答】解:(1)∵△ABD≌△EBC,
∴BD=BC=3cm,BE=AB=2cm,
∴DE=BD﹣BE=1cm;
(2)DB与AC垂直,
理由:∵△ABD≌△EBC,
∴∠ABD=∠EBC,
又A、B、C在一条直线上,
∴∠EBC=90°,
∴DB与AC垂直.
(3)直线AD与直线CE垂直.
理由:如图,延长CE交AD于F,
∵△ABD≌△EBC,
∴∠D=∠C,
∵Rt△ABD中,∠A+∠D=90°,
∴∠A+∠C=90°,
∴∠AFC=90°,即CE⊥AD.
一.选择题
.如图,若△ABD≌△EBC,且AB=3,BC=7,则DE的长为( )
A.2 B.4 C.10 D.3
.已知,图中的两个三角形全等,则∠α等于( )
A.80° B.70° C.60° D.50°
.如图是两个全等三角形,图中的字母表示三角形的边长,则∠1的度数是( )
A.54° B.56° C.60° D.66°
.如图,在△ABC中,AD⊥BC于点D,BE⊥AC于点E,AD,BE交于点F,△ADC
≌△BDF,若BD=4,CD=2,则△ABC的面积为( )
A.24 B.18 C.12 D.8
.如图,在四边形ABCD与四边形A'B'C'D'中,AB=A'B',∠B=∠B',BC=B'C'.下列条件中:①∠A=∠A',AD=A'D';②∠A=∠A',CD=C'D';③∠A=∠A',∠D=∠D';④AD=A'D',CD=C'D'.添加上述条件中的其中一个,可使四边形ABCD≌四边形A'B'C'D'.上述条件中符合要求的有( )
A.①②③ B.①③④ C.①④ D.①②③④
.如图,已知△ABC≌△DEF,CD平分∠BCA,若∠A=22°,∠CGF=88°,则∠E的度数是( )
A.26° B.28° C.30° D.34°
.如图,在△ABC中,ED⊥BC,EA⊥AB,若△EAB≌△EDB≌△EDC,则∠C=( )
A.36° B.30° C.25° D.15°
.两个全等的直角三角形重叠在一起.将其中的一个三角形沿着点B到C的方向平移到△DEF的位置,AB=4,DO=1,平移距离为2.则阴影部分面积为( )
A.7 B.6 C.14 D.4
.如图,N,C,A三点在同一直线上,在△ABC中,∠A:∠ABC:∠ACB=3:5:10,又△MNC≌△ABC,则∠BCM的度数等于( )
A.10° B.20° C.30° D.40°
.如图,锐角△ABC中,D、E分别是AB、AC边上的点,△ADC≌△ADC′,△AEB≌△AEB′,且C′D∥EB′∥BC,BE、CD交于点F.若∠BAC=35°,则∠BFC的大小是( )
A.105° B.110° C.100° D.120°
二.填空题
.如图,D在BC边上,△ABC≌△ADE,∠EAC=40°,则∠B的度数为 .
.如图,点E是CD上的一点,Rt△ACD≌Rt△EBC,则下结论:
①AC=BC,②AD∥BE,③∠ACB=90°,④AD+DE=BE,
成立的有 个.
.如图,在平面直角坐标系中,△OAB的顶点坐标分别是A(﹣6,0),B(0,4),△OA′B′≌△OAB,若点A′在x轴上,则点B′的坐标是 .
.如图,在2×2的方格纸中,∠1+∠2等于 .
.若△ABC≌△DEF,AB=DE=4,△DEF面积为10,则在△ABC中AB边上的高为 .
解答题
.如图,已知△ABC≌△DEF,∠A=85°,∠B=60°,AB=8,EH=2.
(1)求角F的度数与DH的长;
(2)求证:AB∥DE.
.如图,△ABC≌△DEB,点E在边AB上,DE与AC相交于点F.若DE=9,BC=4,∠D=25°,∠C=70°.
(1)求线段AE的长;
(2)求∠DBC的度数.
.已知:如图,点E在线段BC上,且△ABC≌△AED.
求证:(1)∠B=∠AEB;
(2)AE平分∠BED.
.如图,已知△ABC≌△DEB,点E在AB上,DE与AC相交于点F.
(1)当DE=8,BC=5时,求线段AE的长;
(2)已知∠D=35°,∠C=60°,求∠DBC与∠AFD的度数.
.如图,点A、B、C在同一直线上,点E在BD上,且△ABD≌△EBC,AB=2cm,BC=3cm.
(1)求DE的长;
(2)判断AC与BD的位置关系,并说明理由.
(3)判断直线AD与直线CE的位置关系,并说明理由.
参考答案与试题解析
一.选择题
.【解答】解:∵△ABD≌△EBC,
∴AB=BE=3,BD=BC=7,
∴DE=BD﹣BE=7﹣3=4,
故选:B.
.【解答】解:∵△ABC≌△A′B′C′,
∴∠A′=∠A,
∵∠A=180°﹣∠B﹣∠C=180°﹣60°﹣50°=70°,
∴∠A′=70°,
故选:B.
.【解答】解:
∵△ABC≌△DEF,
∴∠F=∠C=∠1,
∵∠A=54°,∠B=60°,
∴∠1=∠C=180°﹣∠A﹣∠B=180°﹣54°﹣60°=66°,
故选:D.
.【解答】解:∵△ADC≌△BDF,
∴AD=BD,
∵BD=4,
∴AD=4,
∵DC=2,
∴BC=BD+DC=4+2=6,
∴S△ABC===12,
故选:C.
.【解答】解:符合要求的条件是①③④,
证明:连接AC、A′C′,
在△ABC与△A′B′C′中,
,
∴△ABC≌△A′B′C′(SAS),
∴AC=A′C′,∠ACB=∠A′C′B′,∠ACB=∠A′C′B′,
∵∠BAD=∠B′A′D′,
∴∠BAD﹣∠DAC=∠B′A′D′﹣∠D′A′C′,
∴∠DAC=∠D′A′C′,
在△ACD和△A′C′D中,
,
∴△ACD≌△A′C′D′(SAS),
∴∠D=∠D′,∠ACD=∠A′C′D′,CD=C′D′,
∴∠BCD=∠B′C′D′,
∴四边形ABCD和四边形A′B′C′D′中,
AB=A′B′,BC=B′C′,AD=A′D′,DC=D′C′,
∠B=∠B′,∠BCD=∠B′C′D′,∠D=∠D′,∠BAD=∠B′A′D′,
∴四边形ABCD≌四边形A′B′C′D′.
同理根据③④的条件证得四边形ABCD≌四边形A′B′C′D′.
故选:B.
.【解答】解:∵△ABC≌△DEF,∠A=22°,
∴∠D=∠A=22°,∠B=∠E,
∴∠E+∠F=180°﹣∠D=180°﹣22°=158°,
在四边形ECGF中,∠ECG=360°﹣∠CGF﹣(∠E+∠F)=360°﹣88°﹣158°=114°,
∴∠DCB=180°﹣∠ECG=180°﹣114°=66°,
∵CD平分∠BCA,
∴∠BCA=2∠DCB=132°,
∴∠E=∠B=180°﹣∠A﹣∠BCA=180°﹣22°﹣132°=26°,
故选:A.
.【解答】解:∵EA⊥AB,
∴∠A=90°,
∵△EAB≌△EDB≌△EDC,
∴∠C=∠EBD,∠ABE=∠EBD,
∴∠C=∠ABE=∠EBD,
∵∠ABC+∠C=90°,
∴3∠C=90°,
∴∠C=30°,
故选:B.
.【解答】解:由平移的性质可知,△ABC≌△DEF,
∴DE=AB=4,BE=2,S△ABC=S△DEF,
∴OE=DE﹣DO=4﹣1=3,
∴阴影部分的面积=S△ABC﹣S△OEC=S梯形ABEO=×(4+3)×2=7,
故选:A.
.【解答】解:∵在△ABC中,∠A:∠ABC:∠ACB=3:5:10,∠A+∠ABC+∠ACB=180°,
∴∠A=30°,∠BCA=100°,∠ABC=50°,
∵△MNC≌△ABC,
∴∠NCM=∠ACB=100°,∠N=∠ABC=50°,BC=NC,
∴∠NBC=∠N=50°,
∴∠BCN=180°﹣∠N﹣∠NBC=80°,
∴∠BCM=∠ACB﹣∠BCN=100°﹣80°=20°,
故选:B.
.【解答】解:设∠C′=α,∠B′=β,
∵△ADC≌△ADC′,△AEB≌△AEB′,
∴∠ACD=∠C′=α,∠ABE=∠B′=β,∠BAE=∠B′AE=35°,
∴∠C′DB=∠BAC′+AC′D=35°+α,∠CEB′=35°+β.
∵C′D∥EB′∥BC,
∴∠ABC=∠C′DB=35°+α,∠ACB=∠CEB′=35°+β,
∴∠BAC+∠ABC+∠ACB=180°,即105°+α+β=180°.
则α+β=75°.
∵∠BFC=∠BDC+∠DBE,
∴∠BFC=35°+α+β=35°+75°=110°.
故选:B.
二.填空题
.【解答】解:∵△ABC≌△ADE,
∴AB=AD,∠BAC=∠DAE,
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,
∴∠BAD=∠EAC,
∵∠EAC=40°,
∴∠BAD=40°,
∵AB=AD,
∴∠B=∠ADB=(180°﹣∠BAD)=70°,
故答案为:70°.
.【解答】解:
∵Rt△ACD≌Rt△EBC,
∴AC=BE,
∵在Rt△BEC中,BE<BC,
∴AC<BC,∴①错误;
∵∠CAD=∠CEB=∠BED=90°,∠D<∠CAD,
∴∠D≠∠BED,
∴AD和BE不平行,∴②错误;
∵Rt△ACD≌Rt△EBC,
∴∠ACD=∠CEE,∠D=∠BCE,
∵∠CAD=90°,
∴∠ACD+∠D=90°,
∴∠ACB=∠ACD+∠BDE=90°,∴③正确;
∵Rt△ACD≌Rt△EBC,
∴AD=CE,CD=BC,
CD=CE+DE=AD+DE=BC,
∵BE<BC,
∴AD+DE>BE,∴④错误;
故答案为:1.
.【解答】解:∵A(﹣6,0),B(0,4),△OA′B′≌△AOB,
∴OA=OA′=6,OB=A′B′=4,
∴点B′的坐标是(6,﹣4),
故答案为:(6,﹣4).
.【解答】解:如图,在△ABC和△DEA中,
,
∴△ABC≌△DEA(SAS),
∴∠2=∠3,
在Rt△ABC中,∠1+∠3=90°,
∴∠1+∠2=90°,
故答案为:90°.
.【解答】解:设△ABC的边AB上的高为h,
∵△ABC≌△DEF,△DEF面积为10,
∴△BAC的面积是10,
∵AB=4,
∴h=10,
解得:h=5,
即△ABC中AB边上的高为5,
故答案为:5.
三.解答题
.【解答】解:(1)∵∠A=85°,∠B=60°,
∴∠ACB=180°﹣∠A﹣∠B=35°,
∵△ABC≌△DEF,AB=8,
∴∠F=∠ACB=35°,DE=AB=8,
∵EH=2,
∴DH=8﹣2=6;
(2)证明:∵△ABC≌△DEF,
∴∠DEF=∠B,
∴AB∥DE.
.【解答】解:(1)∵△ABC≌△DEB,BC=4,DE=9,
∴AB=DE=9,BE=BC=4,
∴AE=AB﹣BE=9﹣4=5;
(2)∵△ABC≌△DEB,∠D=25°,∠C=70°,
∴∠DBA=∠C=70°,∠A=∠D=25°,
∴∠ABC=180°﹣∠C﹣∠A=180°﹣70°﹣25°=85°,
∴∠DBC=∠ABC﹣∠DBA=85°﹣70°=15°.
.【解答】证明:(1)∵△ABC≌△AED,
∴AB=AE,
∴∠B=∠AEB;
(2)∵△ABC≌△AED,
∴∠B=∠AED,
又∠B=∠AEB,
∴∠AED=∠AEB,
∴AE平分∠BED.
.【解答】解:(1)∵△ABC≌△DEB,DE=8,BC=5,
∴AB=DE=8,BE=BC=5,
∴AE=AB=BE=8﹣5=3;
(2)∵△ABC≌△DEB,∠D=35°,∠C=60°,
∴∠DBE=∠C=60°,∠A=∠D=35°,∠ABC=∠DEB,
∴∠ABC=180°﹣∠A﹣∠C=85°,
∴∠DBC=∠ABC﹣∠DBE=85°﹣60°=25°,
∵∠ABC=85°,
∴∠DEB=85°,
∴∠AED=95°,
∴∠AFD=∠A+∠AED=35°+95°=130°.
.【解答】解:(1)∵△ABD≌△EBC,
∴BD=BC=3cm,BE=AB=2cm,
∴DE=BD﹣BE=1cm;
(2)DB与AC垂直,
理由:∵△ABD≌△EBC,
∴∠ABD=∠EBC,
又A、B、C在一条直线上,
∴∠EBC=90°,
∴DB与AC垂直.
(3)直线AD与直线CE垂直.
理由:如图,延长CE交AD于F,
∵△ABD≌△EBC,
∴∠D=∠C,
∵Rt△ABD中,∠A+∠D=90°,
∴∠A+∠C=90°,
∴∠AFC=90°,即CE⊥AD.
