人教版八年级数学上册12.3角的平分线的性质 精选练习 (含解析)
文档属性
| 名称 | 人教版八年级数学上册12.3角的平分线的性质 精选练习 (含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 669.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-09 08:44:37 | ||
图片预览


文档简介
12.3 角的平分线的性质精选练习(含答案)-人教版八年级上册
一.选择题
.如图,是尺规作图中“画一个角等于已知角”的示意图,该作法运用了“全等三角形的对应角相等”这一性质,则判定图中两三角形全等的条件是( )
A.SAS B.ASA C.AAS D.SSS
.如图,四边形ABCD中,∠A=90°,AD=3,连接BD,BD⊥CD,垂足是D且∠ADB=∠C,点P是边BC上的一动点,则DP的最小值是( )
A.1 B.2 C.3 D.4
.如图,在△ABC中,∠ACB=90°,BE平分∠ABC,CF⊥AB,交AB于点F,交BE于点D,若BC=8cm,DF=3cm,则△CDB的面积为( )
A.12cm2 B.8cm2 C.6cm2 D.4cm2
.如图,点P在∠AOB的平分线上,PC⊥OA于点C,∠AOB=30°,点D在边OB上,且OD=DP=2.则线段PC的长度为( )
A.3 B.2 C.1 D.
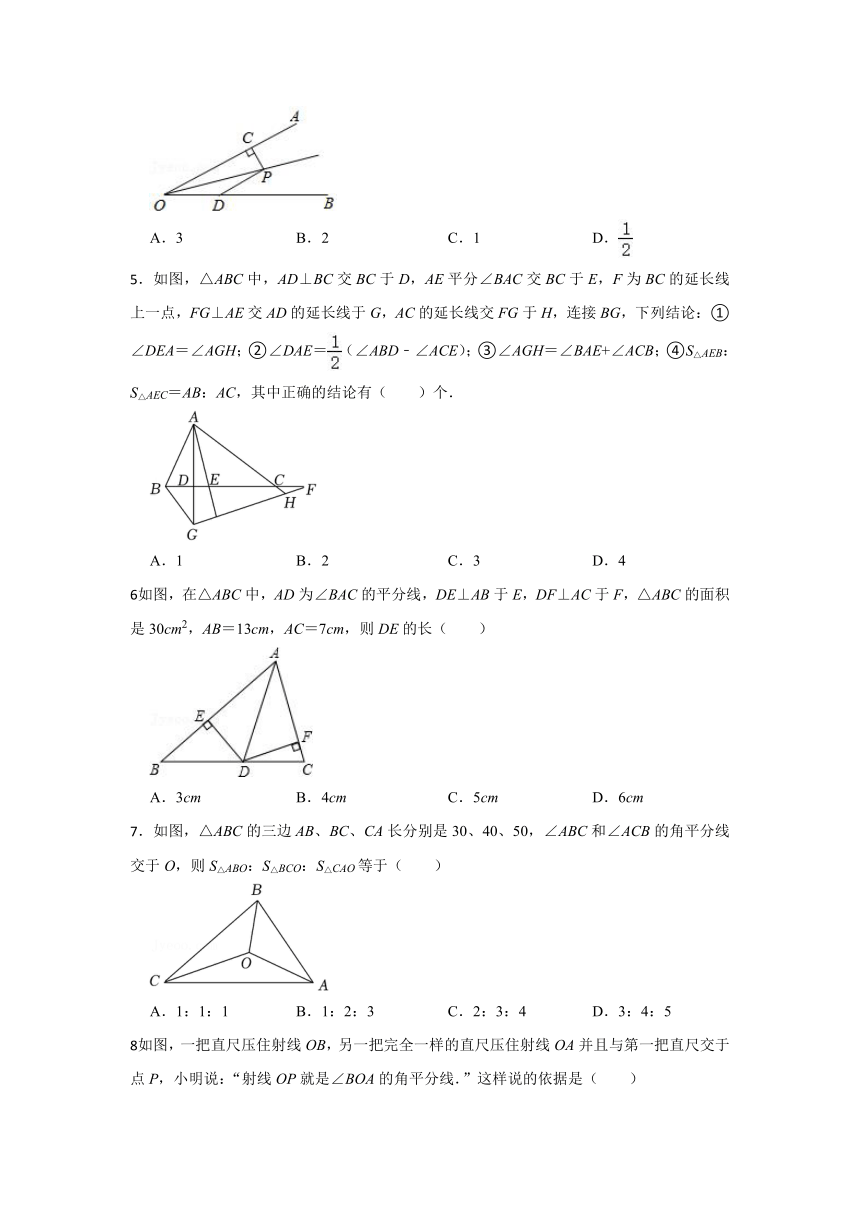
.如图,△ABC中,AD⊥BC交BC于D,AE平分∠BAC交BC于E,F为BC的延长线上一点,FG⊥AE交AD的延长线于G,AC的延长线交FG于H,连接BG,下列结论:①∠DEA=∠AGH;②∠DAE=(∠ABD﹣∠ACE);③∠AGH=∠BAE+∠ACB;④S△AEB:S△AEC=AB:AC,其中正确的结论有( )个.
A.1 B.2 C.3 D.4
如图,在△ABC中,AD为∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,△ABC的面积是30cm2,AB=13cm,AC=7cm,则DE的长( )
A.3cm B.4cm C.5cm D.6cm
.如图,△ABC的三边AB、BC、CA长分别是30、40、50,∠ABC和∠ACB的角平分线交于O,则S△ABO:S△BCO:S△CAO等于( )
A.1:1:1 B.1:2:3 C.2:3:4 D.3:4:5
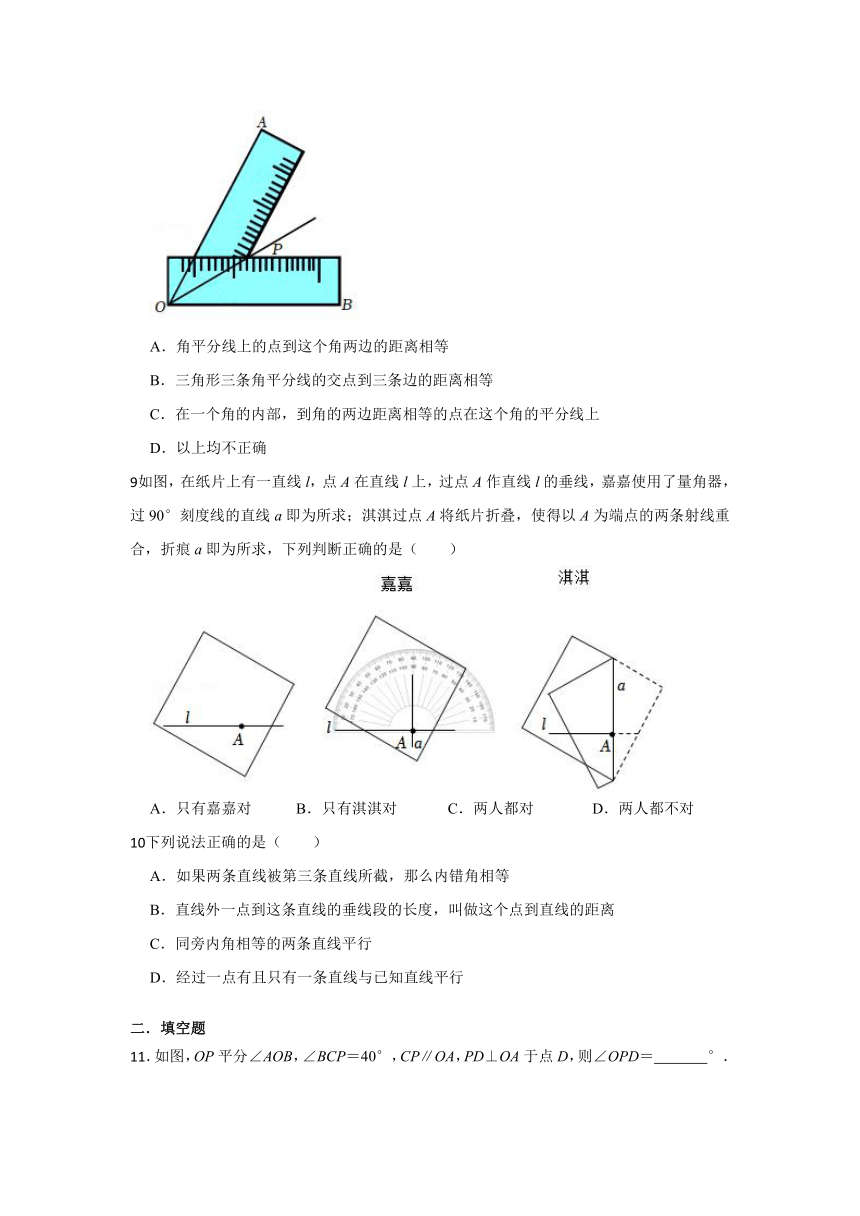
如图,一把直尺压住射线OB,另一把完全一样的直尺压住射线OA并且与第一把直尺交于点P,小明说:“射线OP就是∠BOA的角平分线.”这样说的依据是( )
A.角平分线上的点到这个角两边的距离相等
B.三角形三条角平分线的交点到三条边的距离相等
C.在一个角的内部,到角的两边距离相等的点在这个角的平分线上
D.以上均不正确
如图,在纸片上有一直线l,点A在直线l上,过点A作直线l的垂线,嘉嘉使用了量角器,过90°刻度线的直线a即为所求;淇淇过点A将纸片折叠,使得以A为端点的两条射线重合,折痕a即为所求,下列判断正确的是( )
A.只有嘉嘉对 B.只有淇淇对 C.两人都对 D.两人都不对
下列说法正确的是( )
A.如果两条直线被第三条直线所截,那么内错角相等
B.直线外一点到这条直线的垂线段的长度,叫做这个点到直线的距离
C.同旁内角相等的两条直线平行
D.经过一点有且只有一条直线与已知直线平行
二.填空题
.如图,OP平分∠AOB,∠BCP=40°,CP∥OA,PD⊥OA于点D,则∠OPD= °.
.如图,OP平分∠MON,PA⊥ON于点A,点Q是射线OM上一个动点,若PA=8,则PQ的最小值为 .
.如图,△ABC中,∠C=90°,AD平分∠BAC,CD=2,则点D到AB的距离是 .
.如图,AD是△ABC的角平分线,DF⊥AB,垂足为F,DE=DG,△ADG和△AED的面积分别为27和16,则△EDF的面积为 .
.如图,若P是∠BAC的平分线AD上一点,PE⊥AC于点E,且PE=3,AE=4,点F在边AB上运动,当运动到某一位置时,△FAP的面积恰好是△EAP面积的,则此时AF的长是 .
解答题
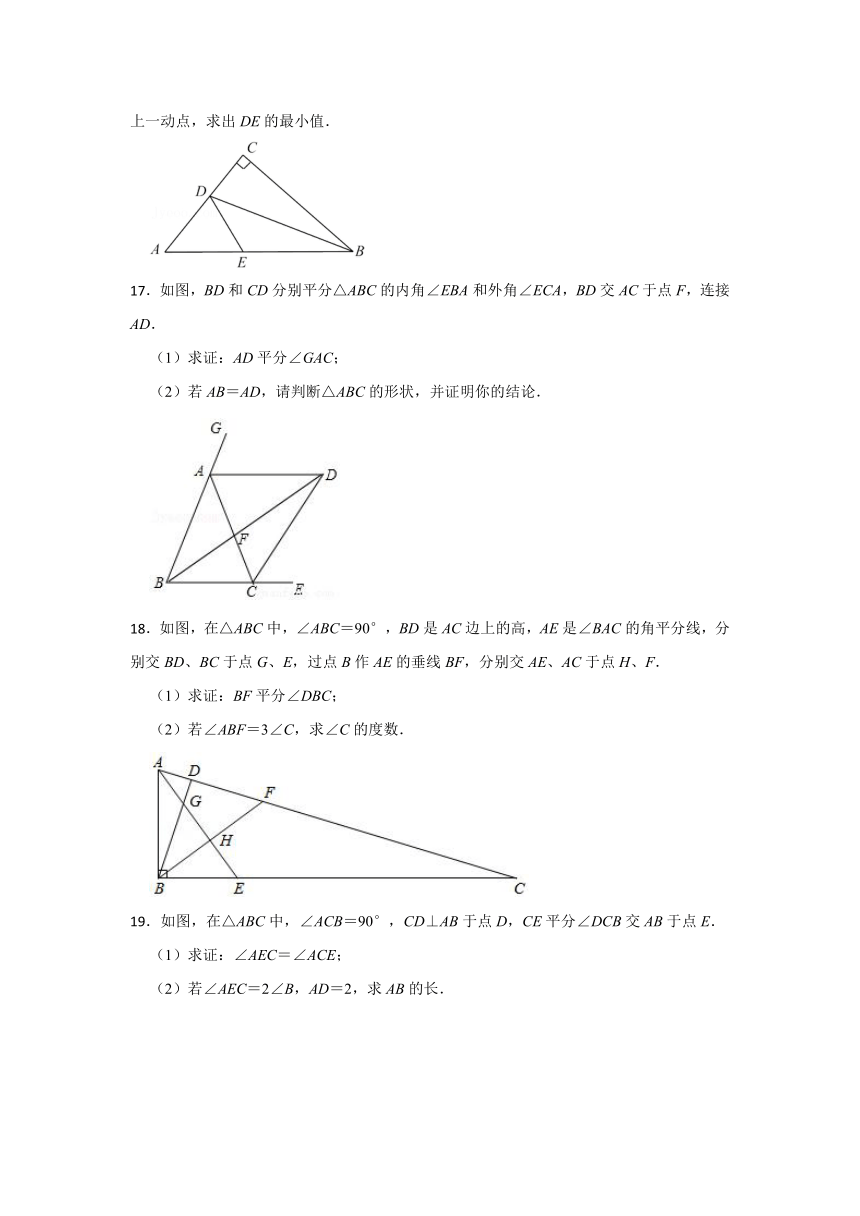
.如图,在△ABC中,∠C=90°,BD平分∠ABC,交AC于点D.若CD=2,E为AB上一动点,求出DE的最小值.
.如图,BD和CD分别平分△ABC的内角∠EBA和外角∠ECA,BD交AC于点F,连接AD.
(1)求证:AD平分∠GAC;
(2)若AB=AD,请判断△ABC的形状,并证明你的结论.
.如图,在△ABC中,∠ABC=90°,BD是AC边上的高,AE是∠BAC的角平分线,分别交BD、BC于点G、E,过点B作AE的垂线BF,分别交AE、AC于点H、F.
(1)求证:BF平分∠DBC;
(2)若∠ABF=3∠C,求∠C的度数.
.如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,CE平分∠DCB交AB于点E.
(1)求证:∠AEC=∠ACE;
(2)若∠AEC=2∠B,AD=2,求AB的长.
.在△ABC中,AE、BF是角平分线,交于O点.
(1)如图1,AD是高,∠BAC=50°,∠C=70°,求∠DAC和∠BOA的度数.
(2)如图2,若OE=OF,AC≠BC,求∠C的度数.
(3)如图3,若∠C=90°,BC=8,AC=6,AB=10,求S△AOB.
参考答案与试题解析
一.选择题
.【解答】解:如图,由作图可知,OA=OB=CE=EF,BA=CF.
在△AOB和△CEF中,
,
∴△AOB≌△CEF(SSS),
故选:D.
.【解答】解:∵BD⊥CD,∠A=90°.
∴∠ABD+∠ADB=90°,
∠CBD+∠C=90°,
∴∠ABD=∠CBD,
由垂线段最短得,DP⊥BC时DP最小,
此时,DP=AD=3.
故选:C.
.【解答】解:作DH⊥BC于点H,如图:
∵BE平分∠ABC,CF⊥AB,DH⊥BC.
∴DH=DF.
∵DF=3cm.
∴DH=3cm.
∵BC=8cm.
∴△CDB的面积为:=12cm2.
故选:A.
.【解答】解:过P作PE⊥OB于E,
∵点P在∠AOB的平分线上,PC⊥OA,
∴PC=PE,∠AOP=∠BOP,
∵OD=DP,
∴∠BOP=∠DPO,
∴∠AOP=∠DPO,
∴PD∥OA,
∴∠PDE=∠AOB,
∵∠AOB=30°,
∴∠PDE=30°,
∵∠PEO=90°,DP=2,
∴PE=DP=1,
∴PC=1,
故选:C.
.【解答】解:如图,AE交GF于M,
①∵AD⊥BC,FG⊥AE,
∴∠ADE=∠AMF=90°,
∴∠DEA+∠DAE=∠AGH+∠GAM=90°,
∴∠DEA=∠AGH,故①正确;
②∵AE平分∠BAC交BC于E,
∴∠EAC=∠BAC,
∴∠DAE=90°﹣∠AED,
=90°﹣(∠ACE+∠EAC),
=90°﹣(∠ACE+∠BAC),
=(180°﹣2∠ACE﹣∠BAC),
=(∠ABD﹣∠ACE),
故②正确;
③∵∠DAE=∠F,∠FDG=∠FME=90°,
∴∠AGH=∠MEF,
∵∠MEF=∠CAE+∠ACB,
∴∠AGH=∠CAE+∠ACB,
∴∠AGH=∠BAE+∠ACB,故③正确;
④∵AE平分∠BAC交BC于E,
∴点E到AB和AC的距离相等,
∴S△AEB:S△AEC=AB:AC,故④正确;
故选:D.
【解答】解:∵AD为∠BAC的平分线,DE⊥AB,DF⊥AC,
∴DE=DF,
∴S△ABC=×AB×DE+×AC×DF=30,即×13×DE+×7×DF=30,
解得DE=DF=3,
故选:A.
【解答】解:过O分别作OE⊥AB,FO⊥BC,OD⊥AC,
∵BO是∠ABC平分线,
∴EO=FO,
∵CO是∠ACB平分线,
∴EO=DO,
∴EO=DO=FO,
∵S△ABO=AB EO,S△BCO=CB FO,S△CAO=AC DO,
∴S△ABO:S△BCO:S△CAO=30:40:50=3:4:5.
故选:D.
【解答】解:如图,过点P作PE⊥AO,PF⊥BO,垂足分别为E和F,
∵两把完全相同的长方形直尺的宽度相等,
∴PE=PF,
∴OP平分∠AOB(角的内部到角的两边的距离相等的点在这个角的平分线上),
故选:C.
【解答】解:嘉嘉利用量角器画90°角,可以画垂线,方法正确.
淇淇过点A将纸片折叠,使得以A为端点的两条射线重合,折痕a垂直直线l,方法正确,
故选:C.
【解答】解:A、如果两条平行的直线被第三条直线所截,那么内错角才相等,故该选项不合题意;
B、从直线外一点到这条直线的垂线段的长度,叫做点到直线的距离,故该选项符合题意;
C、同旁内角互补的两条直线平行,故该选项不合题意;
D、经过直线外一点有且只有一条直线与已知直线平行,故该选项不合题意;
故选:B.
二.填空题
.【解答】解:∵CP∥OA,
∴∠AOB=∠BCP=40°,
∵OP平分∠AOB,
∴∠AOP=∠AOB=20°,
∵PD⊥OA,
∴∠OPD=90°﹣20°=70°,
故答案为:70.
.【解答】解:
过P作PE⊥OM于E,当Q和E重合时,PQ的值最小,
∵OP平分∠MON,PA⊥ON,PA=8,
∴PE=PA=8,
即PQ的最小值是8,
故答案为:8.
.【解答】解:如图,过D点作DE⊥AB于点E,则DE即为所求,
∵∠C=90°,AD平分∠BAC,
∴CD=DE(角的平分线上的点到角的两边的距离相等),
∵CD=2,
∴DE=2.
故答案为2.
.【解答】解:过D点作DH⊥AC于H,如图,
∵AD是△ABC的角平分线,DF⊥AB,DH⊥AC,
∴DF=DH,
在Rt△ADF和Rt△ADH中,
,
∴Rt△ADF≌Rt△ADH(HL),
∴S△ADF=S△ADH,
在Rt△EDF和Rt△GDH中,
,
∴Rt△EDF≌Rt△GDH(HL),
∴S△EDF=S△GDH,
∴S△EDF+S△AED=S△ADG﹣S△GDH,
即S△EDF+16=27﹣S△EDF,
∴S△EDF=5.5.
故答案为:5.5.
.【解答】解:
过P作PM⊥AB于M,
∵P是∠BAC的平分线AD上一点,PE⊥AC,PE=3,PM⊥AB,
∴PM=PE=3,∠PEA=90°,
∵AE=4,
∴△PEA的面积=
=
=6,
∵△FAP的面积恰好是△EAP面积的,
∴=,
∵PM=3,
∴AE=2,
故答案为:2.
三.解答题
.【解答】解:
当DE⊥AB时,DE的值最小(理由是垂线段最短),
∠C=90°,BD平分∠ABC,DE⊥AB,
∴DE=CD,
∵CD=2,
∴DE的最小值是2.
.【解答】(1)证明:过点D作DN⊥BA,DK⊥AC,DM⊥BC,垂足分别为点N、K、M.
∵BD、CD分别平分∠EBA、∠ECA,DN⊥BA,DK⊥AC,DM⊥BC,
∴DM=DN=DK,
∴AD平分∠GAC,∠ABD=∠DBC,
∴∠GAD=∠DAC,
∴AD平分∠GAC.
(2)解:△ABC是等腰三角形,
证明:∵AB=AD,
∴∠ABD=∠ADB,
∵BD平分∠ABC,
∴∠ABD=∠CBD,
∴∠ADB=∠CBD,
∴AD∥BC,
∴∠GAD=∠ABC,∠DAC=∠ACB,
∵AD平分∠GAC,
∴∠GAD=∠CAD,
∴∠ABC=∠ACB,
∴△ABC是等腰三角形.
.【解答】(1)证明:∵BD⊥AC,
∴∠BDC=90°,
∵∠ABC=90°,
∴∠ABD+∠DBC=90°,∠DBC+∠C=90°,
∴∠ABD=∠C,
∵AE平分∠BAC,
∴∠BAE=∠CAE,
∵∠BGE=∠ABD+∠BAE,∠BEG=∠C+∠EAC,
∴∠BGE=∠BEG,
∴BG=BE,
∵BF⊥EG,
∴BF平分∠DBC.
(2)解:∵∠ABF=3∠C,∠ABD=∠C,BF平分∠DBC,
∴∠FBD=∠FBC=2∠C,
∴5∠C=90°,
∴∠C=18°.
.【解答】解:(1)∵∠ACB=90°,CD⊥AB,
∴∠ACD+∠A=∠B+∠A=90°,
∴∠ACD=∠B,
∵CE平分∠BCD,
∴∠BCE=∠DCE,
∴∠B+∠BCE=∠ACD+∠DCE,
即∠AEC=∠ACE;
(2)∵∠AEC=∠B+∠BCE,∠AEC=2∠B,
∴∠B=∠BCE,
又∵∠ACD=∠B,∠BCE=∠DCE,
∴∠ACD=∠BCE=∠DCE,
又∵∠ACB=90°,
∴∠ACD=30°,∠B=30°,
∴Rt△ACD中,AC=2AD=4,
∴Rt△ABC中,AB=2AC=8.
60.【解答】解:(1)∵AD⊥BC,
∴∠ADC=90°,
∵∠C=70°,
∴∠DAC=180°﹣90°﹣70°=20°;
∵∠BAC=50°,∠C=70°,
∴∠BAO=25°,∠ABC=60°,
∵BF是∠ABC的角平分线,
∴∠ABO=30°,
∴∠BOA=180°﹣∠BAO﹣∠ABO=180°﹣25°﹣30°=125°;
(2)连接OC,
∵AE、BF是角平分线,交于O点,
∴OC是∠ACB的角平分线,
∴∠OCF=∠OCE,
过O作OM⊥BC,ON⊥AC,
则OM=ON,
在Rt△OEM与Rt△OFN中,,
∴Rt△OEM≌Rt△OFN,(HL),
∴∠EOM=∠FON,
∴∠MON=∠EOF=180°﹣∠ACB,
∵AE、BF是角平分线,
∴∠AOB=90°+∠ACB,
即90°+∠ACB=180°﹣∠ACB,
∴∠ACB=60°;
(3)连接OC,过O作OD⊥AB于D,OG⊥BC于G,OH⊥AC于H,
∵AE、BF是角平分线,交于O点,
∴OD=OG=OH,
∴S△ABC=×8×6=×10OD+6×OG+8×OH,
∴OD=2,
∴S△AOB=10×2=10.
一.选择题
.如图,是尺规作图中“画一个角等于已知角”的示意图,该作法运用了“全等三角形的对应角相等”这一性质,则判定图中两三角形全等的条件是( )
A.SAS B.ASA C.AAS D.SSS
.如图,四边形ABCD中,∠A=90°,AD=3,连接BD,BD⊥CD,垂足是D且∠ADB=∠C,点P是边BC上的一动点,则DP的最小值是( )
A.1 B.2 C.3 D.4
.如图,在△ABC中,∠ACB=90°,BE平分∠ABC,CF⊥AB,交AB于点F,交BE于点D,若BC=8cm,DF=3cm,则△CDB的面积为( )
A.12cm2 B.8cm2 C.6cm2 D.4cm2
.如图,点P在∠AOB的平分线上,PC⊥OA于点C,∠AOB=30°,点D在边OB上,且OD=DP=2.则线段PC的长度为( )
A.3 B.2 C.1 D.
.如图,△ABC中,AD⊥BC交BC于D,AE平分∠BAC交BC于E,F为BC的延长线上一点,FG⊥AE交AD的延长线于G,AC的延长线交FG于H,连接BG,下列结论:①∠DEA=∠AGH;②∠DAE=(∠ABD﹣∠ACE);③∠AGH=∠BAE+∠ACB;④S△AEB:S△AEC=AB:AC,其中正确的结论有( )个.
A.1 B.2 C.3 D.4
如图,在△ABC中,AD为∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,△ABC的面积是30cm2,AB=13cm,AC=7cm,则DE的长( )
A.3cm B.4cm C.5cm D.6cm
.如图,△ABC的三边AB、BC、CA长分别是30、40、50,∠ABC和∠ACB的角平分线交于O,则S△ABO:S△BCO:S△CAO等于( )
A.1:1:1 B.1:2:3 C.2:3:4 D.3:4:5
如图,一把直尺压住射线OB,另一把完全一样的直尺压住射线OA并且与第一把直尺交于点P,小明说:“射线OP就是∠BOA的角平分线.”这样说的依据是( )
A.角平分线上的点到这个角两边的距离相等
B.三角形三条角平分线的交点到三条边的距离相等
C.在一个角的内部,到角的两边距离相等的点在这个角的平分线上
D.以上均不正确
如图,在纸片上有一直线l,点A在直线l上,过点A作直线l的垂线,嘉嘉使用了量角器,过90°刻度线的直线a即为所求;淇淇过点A将纸片折叠,使得以A为端点的两条射线重合,折痕a即为所求,下列判断正确的是( )
A.只有嘉嘉对 B.只有淇淇对 C.两人都对 D.两人都不对
下列说法正确的是( )
A.如果两条直线被第三条直线所截,那么内错角相等
B.直线外一点到这条直线的垂线段的长度,叫做这个点到直线的距离
C.同旁内角相等的两条直线平行
D.经过一点有且只有一条直线与已知直线平行
二.填空题
.如图,OP平分∠AOB,∠BCP=40°,CP∥OA,PD⊥OA于点D,则∠OPD= °.
.如图,OP平分∠MON,PA⊥ON于点A,点Q是射线OM上一个动点,若PA=8,则PQ的最小值为 .
.如图,△ABC中,∠C=90°,AD平分∠BAC,CD=2,则点D到AB的距离是 .
.如图,AD是△ABC的角平分线,DF⊥AB,垂足为F,DE=DG,△ADG和△AED的面积分别为27和16,则△EDF的面积为 .
.如图,若P是∠BAC的平分线AD上一点,PE⊥AC于点E,且PE=3,AE=4,点F在边AB上运动,当运动到某一位置时,△FAP的面积恰好是△EAP面积的,则此时AF的长是 .
解答题
.如图,在△ABC中,∠C=90°,BD平分∠ABC,交AC于点D.若CD=2,E为AB上一动点,求出DE的最小值.
.如图,BD和CD分别平分△ABC的内角∠EBA和外角∠ECA,BD交AC于点F,连接AD.
(1)求证:AD平分∠GAC;
(2)若AB=AD,请判断△ABC的形状,并证明你的结论.
.如图,在△ABC中,∠ABC=90°,BD是AC边上的高,AE是∠BAC的角平分线,分别交BD、BC于点G、E,过点B作AE的垂线BF,分别交AE、AC于点H、F.
(1)求证:BF平分∠DBC;
(2)若∠ABF=3∠C,求∠C的度数.
.如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,CE平分∠DCB交AB于点E.
(1)求证:∠AEC=∠ACE;
(2)若∠AEC=2∠B,AD=2,求AB的长.
.在△ABC中,AE、BF是角平分线,交于O点.
(1)如图1,AD是高,∠BAC=50°,∠C=70°,求∠DAC和∠BOA的度数.
(2)如图2,若OE=OF,AC≠BC,求∠C的度数.
(3)如图3,若∠C=90°,BC=8,AC=6,AB=10,求S△AOB.
参考答案与试题解析
一.选择题
.【解答】解:如图,由作图可知,OA=OB=CE=EF,BA=CF.
在△AOB和△CEF中,
,
∴△AOB≌△CEF(SSS),
故选:D.
.【解答】解:∵BD⊥CD,∠A=90°.
∴∠ABD+∠ADB=90°,
∠CBD+∠C=90°,
∴∠ABD=∠CBD,
由垂线段最短得,DP⊥BC时DP最小,
此时,DP=AD=3.
故选:C.
.【解答】解:作DH⊥BC于点H,如图:
∵BE平分∠ABC,CF⊥AB,DH⊥BC.
∴DH=DF.
∵DF=3cm.
∴DH=3cm.
∵BC=8cm.
∴△CDB的面积为:=12cm2.
故选:A.
.【解答】解:过P作PE⊥OB于E,
∵点P在∠AOB的平分线上,PC⊥OA,
∴PC=PE,∠AOP=∠BOP,
∵OD=DP,
∴∠BOP=∠DPO,
∴∠AOP=∠DPO,
∴PD∥OA,
∴∠PDE=∠AOB,
∵∠AOB=30°,
∴∠PDE=30°,
∵∠PEO=90°,DP=2,
∴PE=DP=1,
∴PC=1,
故选:C.
.【解答】解:如图,AE交GF于M,
①∵AD⊥BC,FG⊥AE,
∴∠ADE=∠AMF=90°,
∴∠DEA+∠DAE=∠AGH+∠GAM=90°,
∴∠DEA=∠AGH,故①正确;
②∵AE平分∠BAC交BC于E,
∴∠EAC=∠BAC,
∴∠DAE=90°﹣∠AED,
=90°﹣(∠ACE+∠EAC),
=90°﹣(∠ACE+∠BAC),
=(180°﹣2∠ACE﹣∠BAC),
=(∠ABD﹣∠ACE),
故②正确;
③∵∠DAE=∠F,∠FDG=∠FME=90°,
∴∠AGH=∠MEF,
∵∠MEF=∠CAE+∠ACB,
∴∠AGH=∠CAE+∠ACB,
∴∠AGH=∠BAE+∠ACB,故③正确;
④∵AE平分∠BAC交BC于E,
∴点E到AB和AC的距离相等,
∴S△AEB:S△AEC=AB:AC,故④正确;
故选:D.
【解答】解:∵AD为∠BAC的平分线,DE⊥AB,DF⊥AC,
∴DE=DF,
∴S△ABC=×AB×DE+×AC×DF=30,即×13×DE+×7×DF=30,
解得DE=DF=3,
故选:A.
【解答】解:过O分别作OE⊥AB,FO⊥BC,OD⊥AC,
∵BO是∠ABC平分线,
∴EO=FO,
∵CO是∠ACB平分线,
∴EO=DO,
∴EO=DO=FO,
∵S△ABO=AB EO,S△BCO=CB FO,S△CAO=AC DO,
∴S△ABO:S△BCO:S△CAO=30:40:50=3:4:5.
故选:D.
【解答】解:如图,过点P作PE⊥AO,PF⊥BO,垂足分别为E和F,
∵两把完全相同的长方形直尺的宽度相等,
∴PE=PF,
∴OP平分∠AOB(角的内部到角的两边的距离相等的点在这个角的平分线上),
故选:C.
【解答】解:嘉嘉利用量角器画90°角,可以画垂线,方法正确.
淇淇过点A将纸片折叠,使得以A为端点的两条射线重合,折痕a垂直直线l,方法正确,
故选:C.
【解答】解:A、如果两条平行的直线被第三条直线所截,那么内错角才相等,故该选项不合题意;
B、从直线外一点到这条直线的垂线段的长度,叫做点到直线的距离,故该选项符合题意;
C、同旁内角互补的两条直线平行,故该选项不合题意;
D、经过直线外一点有且只有一条直线与已知直线平行,故该选项不合题意;
故选:B.
二.填空题
.【解答】解:∵CP∥OA,
∴∠AOB=∠BCP=40°,
∵OP平分∠AOB,
∴∠AOP=∠AOB=20°,
∵PD⊥OA,
∴∠OPD=90°﹣20°=70°,
故答案为:70.
.【解答】解:
过P作PE⊥OM于E,当Q和E重合时,PQ的值最小,
∵OP平分∠MON,PA⊥ON,PA=8,
∴PE=PA=8,
即PQ的最小值是8,
故答案为:8.
.【解答】解:如图,过D点作DE⊥AB于点E,则DE即为所求,
∵∠C=90°,AD平分∠BAC,
∴CD=DE(角的平分线上的点到角的两边的距离相等),
∵CD=2,
∴DE=2.
故答案为2.
.【解答】解:过D点作DH⊥AC于H,如图,
∵AD是△ABC的角平分线,DF⊥AB,DH⊥AC,
∴DF=DH,
在Rt△ADF和Rt△ADH中,
,
∴Rt△ADF≌Rt△ADH(HL),
∴S△ADF=S△ADH,
在Rt△EDF和Rt△GDH中,
,
∴Rt△EDF≌Rt△GDH(HL),
∴S△EDF=S△GDH,
∴S△EDF+S△AED=S△ADG﹣S△GDH,
即S△EDF+16=27﹣S△EDF,
∴S△EDF=5.5.
故答案为:5.5.
.【解答】解:
过P作PM⊥AB于M,
∵P是∠BAC的平分线AD上一点,PE⊥AC,PE=3,PM⊥AB,
∴PM=PE=3,∠PEA=90°,
∵AE=4,
∴△PEA的面积=
=
=6,
∵△FAP的面积恰好是△EAP面积的,
∴=,
∵PM=3,
∴AE=2,
故答案为:2.
三.解答题
.【解答】解:
当DE⊥AB时,DE的值最小(理由是垂线段最短),
∠C=90°,BD平分∠ABC,DE⊥AB,
∴DE=CD,
∵CD=2,
∴DE的最小值是2.
.【解答】(1)证明:过点D作DN⊥BA,DK⊥AC,DM⊥BC,垂足分别为点N、K、M.
∵BD、CD分别平分∠EBA、∠ECA,DN⊥BA,DK⊥AC,DM⊥BC,
∴DM=DN=DK,
∴AD平分∠GAC,∠ABD=∠DBC,
∴∠GAD=∠DAC,
∴AD平分∠GAC.
(2)解:△ABC是等腰三角形,
证明:∵AB=AD,
∴∠ABD=∠ADB,
∵BD平分∠ABC,
∴∠ABD=∠CBD,
∴∠ADB=∠CBD,
∴AD∥BC,
∴∠GAD=∠ABC,∠DAC=∠ACB,
∵AD平分∠GAC,
∴∠GAD=∠CAD,
∴∠ABC=∠ACB,
∴△ABC是等腰三角形.
.【解答】(1)证明:∵BD⊥AC,
∴∠BDC=90°,
∵∠ABC=90°,
∴∠ABD+∠DBC=90°,∠DBC+∠C=90°,
∴∠ABD=∠C,
∵AE平分∠BAC,
∴∠BAE=∠CAE,
∵∠BGE=∠ABD+∠BAE,∠BEG=∠C+∠EAC,
∴∠BGE=∠BEG,
∴BG=BE,
∵BF⊥EG,
∴BF平分∠DBC.
(2)解:∵∠ABF=3∠C,∠ABD=∠C,BF平分∠DBC,
∴∠FBD=∠FBC=2∠C,
∴5∠C=90°,
∴∠C=18°.
.【解答】解:(1)∵∠ACB=90°,CD⊥AB,
∴∠ACD+∠A=∠B+∠A=90°,
∴∠ACD=∠B,
∵CE平分∠BCD,
∴∠BCE=∠DCE,
∴∠B+∠BCE=∠ACD+∠DCE,
即∠AEC=∠ACE;
(2)∵∠AEC=∠B+∠BCE,∠AEC=2∠B,
∴∠B=∠BCE,
又∵∠ACD=∠B,∠BCE=∠DCE,
∴∠ACD=∠BCE=∠DCE,
又∵∠ACB=90°,
∴∠ACD=30°,∠B=30°,
∴Rt△ACD中,AC=2AD=4,
∴Rt△ABC中,AB=2AC=8.
60.【解答】解:(1)∵AD⊥BC,
∴∠ADC=90°,
∵∠C=70°,
∴∠DAC=180°﹣90°﹣70°=20°;
∵∠BAC=50°,∠C=70°,
∴∠BAO=25°,∠ABC=60°,
∵BF是∠ABC的角平分线,
∴∠ABO=30°,
∴∠BOA=180°﹣∠BAO﹣∠ABO=180°﹣25°﹣30°=125°;
(2)连接OC,
∵AE、BF是角平分线,交于O点,
∴OC是∠ACB的角平分线,
∴∠OCF=∠OCE,
过O作OM⊥BC,ON⊥AC,
则OM=ON,
在Rt△OEM与Rt△OFN中,,
∴Rt△OEM≌Rt△OFN,(HL),
∴∠EOM=∠FON,
∴∠MON=∠EOF=180°﹣∠ACB,
∵AE、BF是角平分线,
∴∠AOB=90°+∠ACB,
即90°+∠ACB=180°﹣∠ACB,
∴∠ACB=60°;
(3)连接OC,过O作OD⊥AB于D,OG⊥BC于G,OH⊥AC于H,
∵AE、BF是角平分线,交于O点,
∴OD=OG=OH,
∴S△ABC=×8×6=×10OD+6×OG+8×OH,
∴OD=2,
∴S△AOB=10×2=10.
