平行线等分线段定理[上学期]
文档属性
| 名称 | 平行线等分线段定理[上学期] |  | |
| 格式 | rar | ||
| 文件大小 | 130.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-12-21 14:48:00 | ||
图片预览



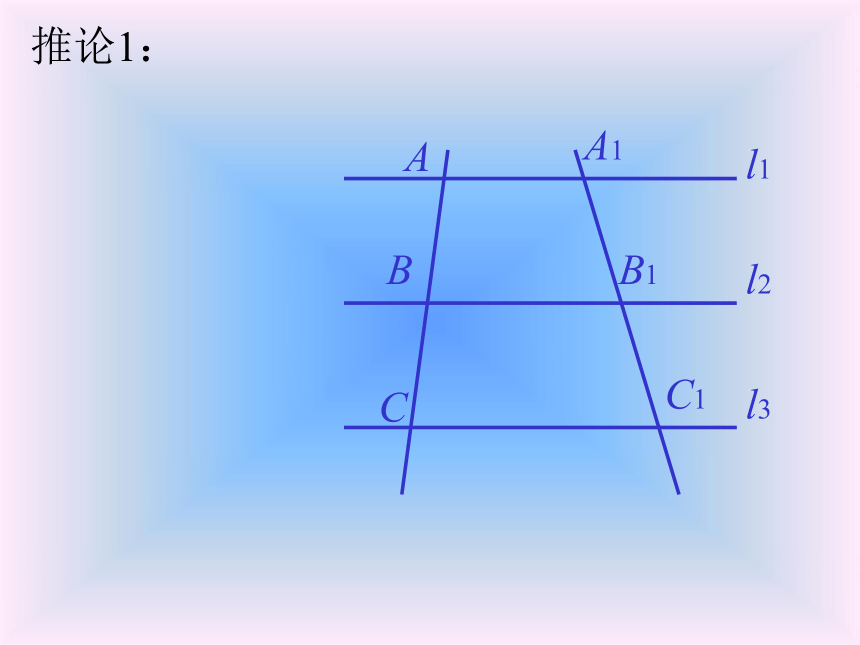
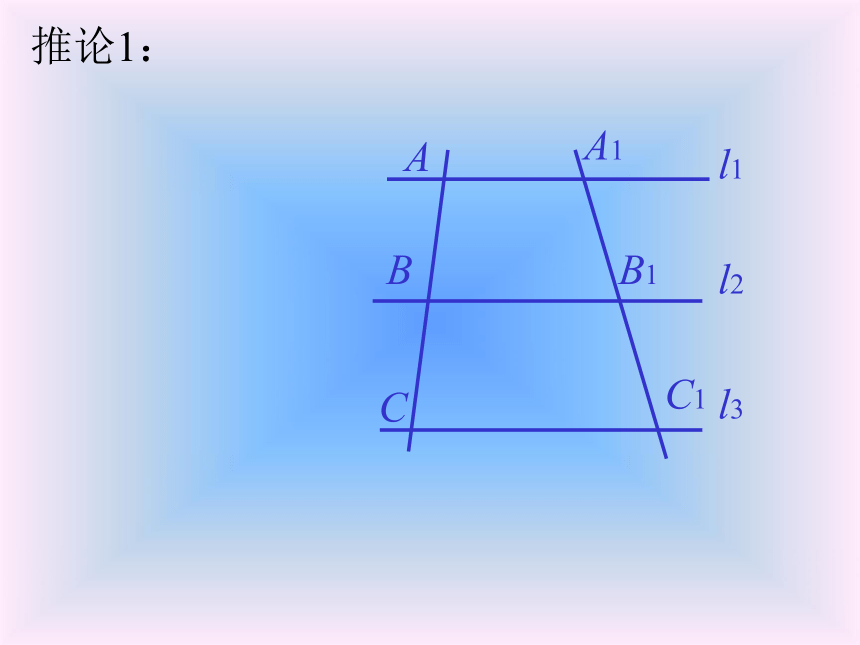

文档简介
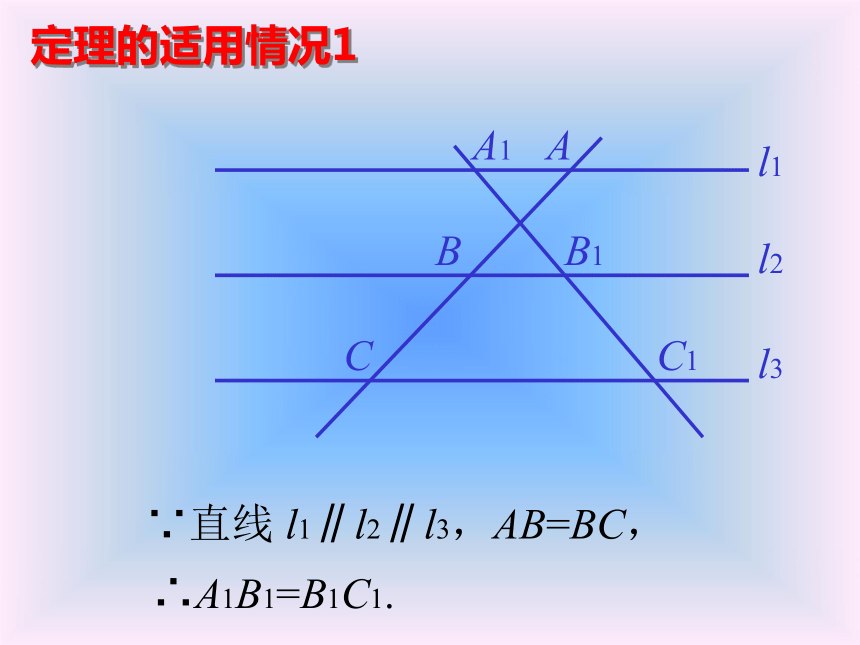
课件68张PPT。平行线等分线段定理定理:如果一组平行线在一条直线上
截得的线段相等,那么在其他直线上截得的线段
也相等.ABC证明:连结AB1、A1B、
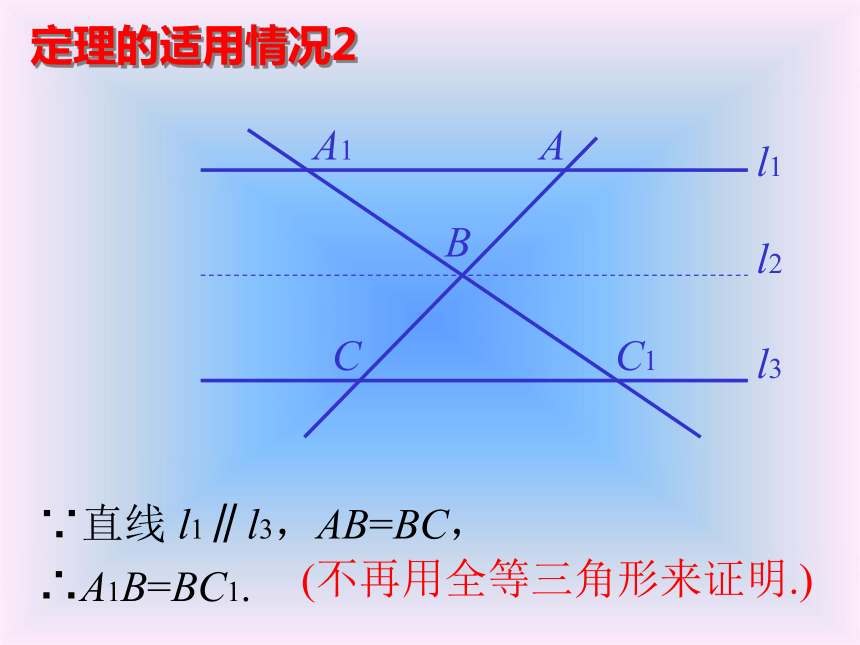
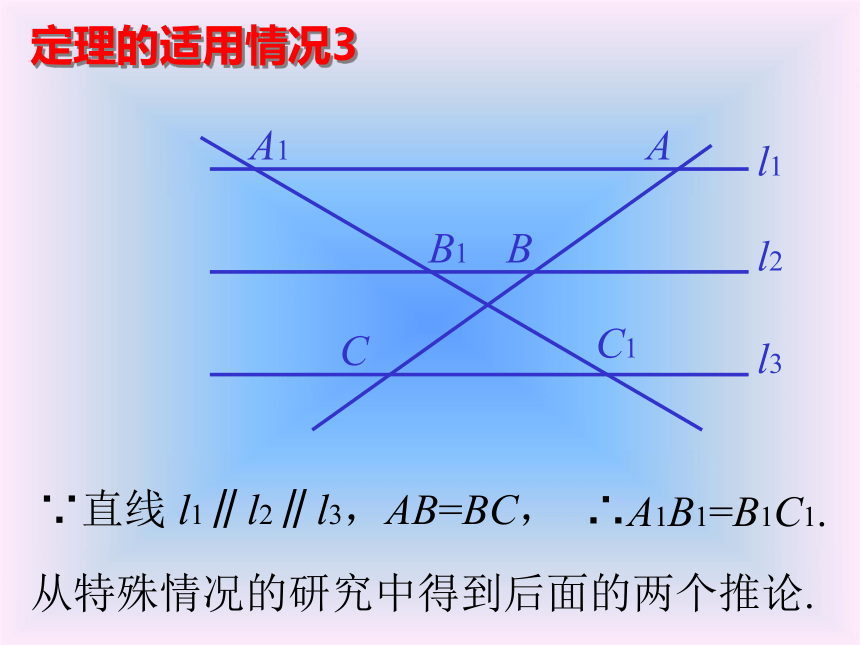
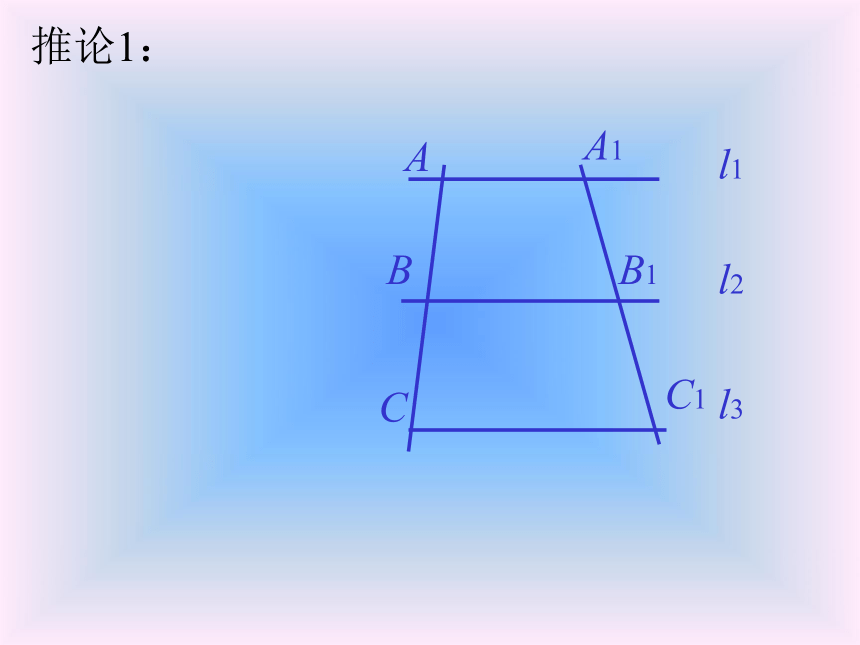
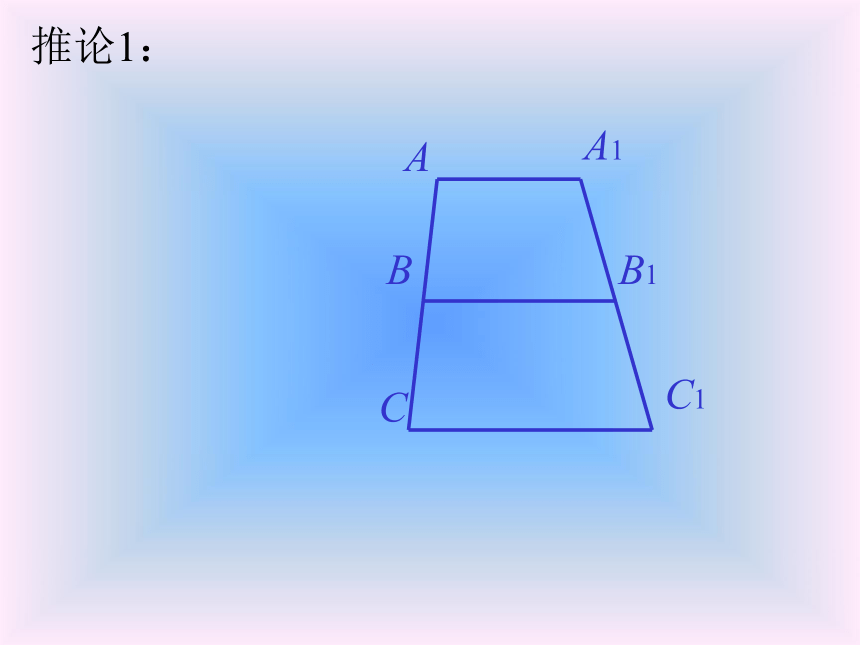
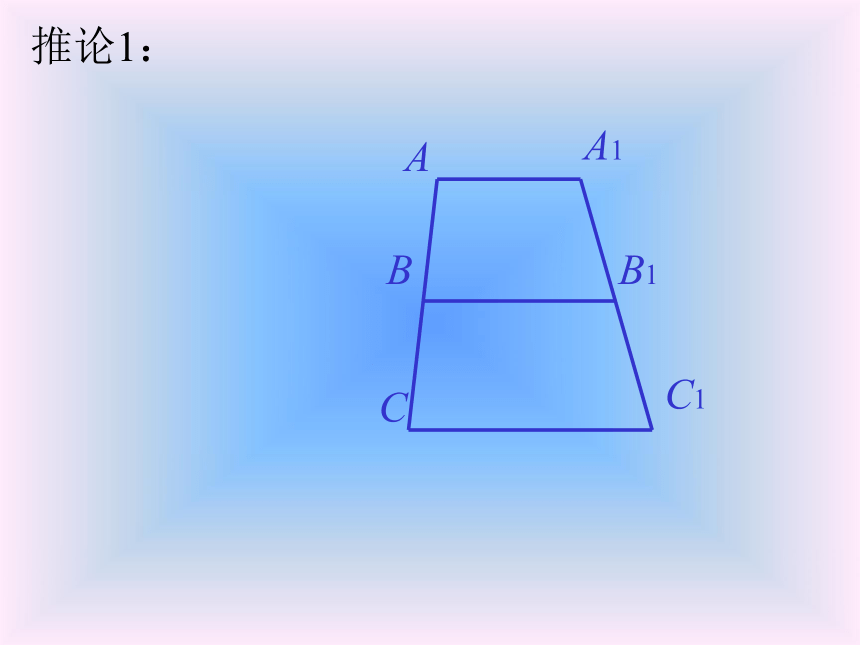
BC1、B1C,∵AB=BC,∴S△ABB1=S△CBB1;∵l1∥l2∥l3,∴A1B1=B1C1.说明:这里是用面积来证明的, 请你注意学习这种方法.l1l2l3A1B1C1∴S△A1BB1=S△C1BB1,已知:直线 l1∥l2∥l3,AB=BC,求证:A1B1=B1C1.∴S△ABB1=S△A1BB1,S△CBB1=S△C1BB1,定理的适用情况1ABCl1l2l3A1B1C1∵直线 l1∥l2∥l3,AB=BC,∴A1B1=B1C1.定理的适用情况2ABCl1l2l3A1C1∵直线 l1∥l3,AB=BC,∴A1B=BC1.(不再用全等三角形来证明.)定理的适用情况3ABCl1l2l3A1B1C1∵直线 l1∥l2∥l3,AB=BC,∴A1B1=B1C1.从特殊情况的研究中得到后面的两个推论.推论1:ABCl1l2l3A1B1C1推论1:ABCl1l2l3A1B1C1推论1:ABCl1l2l3A1B1C1推论1:ABCA1B1C1推论1:ABCA1B1C1推论1:ABCA1B1C1推论1:ABCA1B1C1推论1:ABCA1B1C1推论1:ABCA1B1C1推论1:
经过梯形一腰的中点与底边平行的直线, 必平分另一腰.∴A1B1=B1C1.在梯形 ACC1A1中, AA1∥CC1 ,∵AB=BC, BB1∥CC1,ABCl1l2l3A1B1C1推论2:ABCl1l2l3A1B1C1推论2:ABCl1l2l3A1B1C1推论2:ABCl1l2l3A1B1C1推论2:ABCl1l2l3A1B1C1推论2:ABCl1l2l3A1B1C1推论2:ABCl1l2l3A1B1C1推论2:ABCl1l2l3A1B1C1推论2:ABCl1l2l3A1B1C1推论2:ABCl1l2l3A1B1C1推论2:ABCl1l2l3A1B1C1推论2:ABCB1C1推论2:ABCB1C1推论2:ABCl1l2l3A1B1C1推论2:ABCB1C1推论2:ABCB1C1推论2:推论2:ABCB1C1推论2:
经过三角形一边的中点与另一边平行的直线必平分第三边.在△ACC1中,∴AB1=B1C.AB=BC,BB1∥CC1,ABCB1C1AF交BE于O,且AO=OD=DF,厘米.若BE=60厘米,那么BO=CDEFO20一、填空题1、已知AB∥CD∥EF,AB且AE=BE,那么DF=.CF2、已知AD∥EF∥BC,EFBCADE是AB的中点,则DG=,H是EFBCADGH的中点,.F是的中点BGACCD3、已知AD∥EF∥BC,4、已知△ABC中,AB=AC,AD⊥BC,M是AD的中点,CM交AB于P,DN∥CM交AB于N,如果AB=6厘米,则PN=厘米.2ABCD.MPN∟5、已知△ABC中,CD平分∠ACB,ABCDAE⊥CD交BC于E,EDF∥CB交AB于F,FAF=4厘米,则AB=厘米.8∟二、判断题1、若AB∥CD∥EF,ABCDEFAC=CE,则 BD=DF=AC=CE.( )×则AB∥CD∥EF,2、如图,若 AC=CE,BD=DF,( )×ABCDEFABCDEF3、过平行四边形对角线的交点且平行于一组对边的直线必平分另一组对边。( )√((((4、如图,已知□ABCD中,( )AA1⊥l,BB1⊥l,CC1⊥l,DD1⊥l,连结AC、BD交于点O,作OO1⊥l,则A1B1=C1D1.√ABCDOlA1B1C1D1O1∟∟∟∟∟5、过梯形一腰的中点且平行于底边的直线平分两条对角线及另一腰。( )√PNQ三、证明题1、已知:Rt△ABC中,∠ACB=90°,ABCD为BC边的中点,DDE⊥BC交AB于E,E求证:AB=2CE..∟∟证明:∵∠ACB=90°,∴∠BDE=∠ACB,∴DE∥CA,∵D是BC的中点,∴E是AB的中点,∴AB=2CE.∵DE⊥BC,∴∠BDE=90°;2、已知:□ABCD中,E、F分别是AB、DCABCDEF的中点,MN求证:BM=MN=NC.分析:需证明EC∥AF.证明:∵四边形ABCD是平行四边形,∴AB=DC,AB∥DC;..分别交BD于M、N,∵E、F分别是AB、DC的中点,∴AE=FC,∴四边形AECF是平行四边形,∴EC∥AF,∴BM=MN, MN=ND,即BM=MN=ND. CE、AF3、已知:梯形ABCD中,AD∥BC,ABCDEE是AB边的中点,EF∥DC,交BC于F,F求证:DC=2EF.证明:M作EM∥BC交DC于M,∵E是梯形ABCD的腰AB的中点,∴M是DC的中点,即DC=2MC;∵EF∥DC,∴EF=MC,∴DC=2EF..4、已知:直角梯形ABCD中,AD∥BC,
∠ABC=90°,ABCDEE是DC边的中点,求证:AE=BE.分析:需证E在AB的中垂线上.证明:F作EF∥BC交AB于F,∵E是梯形ABCD的腰DC的中点,∴F是AB的中点;∵EF∥BC,∠ABC=90°,∴∠AFE=∠ABC=90°,∴EF是AB的垂直平分线,∴AE=BE.∟∟.5、已知:△ABC的两中线AD、BE相交于点ABCDEGG,CH∥EB交AD的延长线于点H,H求证:AG=2GD.分析:需要证明GH=2GD=2DH.证明:∵AD、BE是中线,∴AE=EC,BD=DC,∵CH∥EB,∴AG=GH,∴AG=2GD.本题说明三角形的两中线的交点把中线分成2:1的两部分.
这个结论叫做重心定理.(现行课本已把它略去.)GD=DH,6、已知:梯形ABCD中,AD∥BC,ABCDEABDE是平行四边形,AD的延长线交EC于F,F求证:EF=FC.分析:需证明AF、BC在
其他直线上截得
相等的线段.6、已知:梯形ABCD中,AD∥BC,ABCDEABDE是平行四边形,AD的延长线交EC于F,F求证:EF=FC.分析:需证明AF、BC在
其他直线上截得
相等的线段.证法1:O连结BE交AF于点O,∵四边形ABDE是平行四边形,∵AF∥BC,∴EF=FC.∴BO=OE;″′′″ABCDEF证法2:H延长ED交BC于点H,∵四边形ABDE是平行四边形,∵AF∥BC,∴EF=FC.∴四边形ABHD是平行四边形,∴AB=DH,∴ED=DH;∴AB∥ED,即AB∥DH,且AB=ED,′′″″ABCDEF证法3:M′″″′′ABCDEF证法4:N′″″′′证法5:ABCDEFPAAS分析:本题还有多种
构造全等形的证法.
例如:证法6:AASABCDEFQ证法7:ABCDEFSAAS证法8:ABCDEFTAAS证法9:AASABCDEFP证法10:AASABCDEFQ证法11:AASABCDEFS证法12:AASABCDEFT7、已知:△ABC中,AB=AC,D在AB上,F在AC的延长线上,且BD=CF,DF交BC于E,求证:DE=EF.分析:
这是一道应已证过的题。
除用证三角形全等的方法外,
本题还可用平行线等分线段
定理的推论来证明。这里给出动画显示,证明的语句略去。证法1:ABCDEFH))((证法2:ABCDEFH(以下略去。)8、已知:AC⊥AB,DB⊥AB,O是CD的中点,求证:OA=OB.分析:需证明点O在AB的垂直平分线上.证明:作OE⊥AB于E,∵AC⊥AB,DB⊥AB,∴∠CAB=90°,∠DBA=90°,∴∠CAB=∠OEA=∠DBA,∴AC∥OE∥DB;∵O是CD的中点,∴E是AB的中点,∴OE是AB的垂直平分线,∴OA=OB.则∠OEA=90°;ABCDOE∟∟∟9、已知:AD为△ABC的中线,ABCDMPM为AD的中点,直线CM交AB于点P,求证:AP= —13AB.分析:可证明BP=2AP.证明:Q作DQ∥CP交AB于点Q;∵D是BC的中点,M是AD的中点,∴Q是BP的中点,P是AQ的中点,∴AP=PQ=QB,∴AP= —31AB.10、已知:∠ACB=90°,AC=BC,ABC求证:MN=NB.分析:
若结论成立,则过B作NC
的平行线交直线AC必截得
相等的线段,反之亦然.D∟EFMN∟∟CE=CF,EM⊥AF,CN⊥AF,ABC10、证明:D延长AC到D,使CD=CE,
连结DB.∵∠ACB=90°,CN⊥AF,∴∠CAF=∠CBD;∴∠NCF=∠CAF=∠CBD,∵EM⊥AF,∴EM∥CF,∴MN=NB.则△ACF≌△BCD,∟EFMN∟∟∴DB∥CN;∴EM∥CN∥DB,小结:
平行线等分线段定理是一个重要
的定理,在这里是利用面积证明的,
这种证法还可以用于后面即将学到的
平行线分线段成比例定理。
截得的线段相等,那么在其他直线上截得的线段
也相等.ABC证明:连结AB1、A1B、
BC1、B1C,∵AB=BC,∴S△ABB1=S△CBB1;∵l1∥l2∥l3,∴A1B1=B1C1.说明:这里是用面积来证明的, 请你注意学习这种方法.l1l2l3A1B1C1∴S△A1BB1=S△C1BB1,已知:直线 l1∥l2∥l3,AB=BC,求证:A1B1=B1C1.∴S△ABB1=S△A1BB1,S△CBB1=S△C1BB1,定理的适用情况1ABCl1l2l3A1B1C1∵直线 l1∥l2∥l3,AB=BC,∴A1B1=B1C1.定理的适用情况2ABCl1l2l3A1C1∵直线 l1∥l3,AB=BC,∴A1B=BC1.(不再用全等三角形来证明.)定理的适用情况3ABCl1l2l3A1B1C1∵直线 l1∥l2∥l3,AB=BC,∴A1B1=B1C1.从特殊情况的研究中得到后面的两个推论.推论1:ABCl1l2l3A1B1C1推论1:ABCl1l2l3A1B1C1推论1:ABCl1l2l3A1B1C1推论1:ABCA1B1C1推论1:ABCA1B1C1推论1:ABCA1B1C1推论1:ABCA1B1C1推论1:ABCA1B1C1推论1:ABCA1B1C1推论1:
经过梯形一腰的中点与底边平行的直线, 必平分另一腰.∴A1B1=B1C1.在梯形 ACC1A1中, AA1∥CC1 ,∵AB=BC, BB1∥CC1,ABCl1l2l3A1B1C1推论2:ABCl1l2l3A1B1C1推论2:ABCl1l2l3A1B1C1推论2:ABCl1l2l3A1B1C1推论2:ABCl1l2l3A1B1C1推论2:ABCl1l2l3A1B1C1推论2:ABCl1l2l3A1B1C1推论2:ABCl1l2l3A1B1C1推论2:ABCl1l2l3A1B1C1推论2:ABCl1l2l3A1B1C1推论2:ABCl1l2l3A1B1C1推论2:ABCB1C1推论2:ABCB1C1推论2:ABCl1l2l3A1B1C1推论2:ABCB1C1推论2:ABCB1C1推论2:推论2:ABCB1C1推论2:
经过三角形一边的中点与另一边平行的直线必平分第三边.在△ACC1中,∴AB1=B1C.AB=BC,BB1∥CC1,ABCB1C1AF交BE于O,且AO=OD=DF,厘米.若BE=60厘米,那么BO=CDEFO20一、填空题1、已知AB∥CD∥EF,AB且AE=BE,那么DF=.CF2、已知AD∥EF∥BC,EFBCADE是AB的中点,则DG=,H是EFBCADGH的中点,.F是的中点BGACCD3、已知AD∥EF∥BC,4、已知△ABC中,AB=AC,AD⊥BC,M是AD的中点,CM交AB于P,DN∥CM交AB于N,如果AB=6厘米,则PN=厘米.2ABCD.MPN∟5、已知△ABC中,CD平分∠ACB,ABCDAE⊥CD交BC于E,EDF∥CB交AB于F,FAF=4厘米,则AB=厘米.8∟二、判断题1、若AB∥CD∥EF,ABCDEFAC=CE,则 BD=DF=AC=CE.( )×则AB∥CD∥EF,2、如图,若 AC=CE,BD=DF,( )×ABCDEFABCDEF3、过平行四边形对角线的交点且平行于一组对边的直线必平分另一组对边。( )√((((4、如图,已知□ABCD中,( )AA1⊥l,BB1⊥l,CC1⊥l,DD1⊥l,连结AC、BD交于点O,作OO1⊥l,则A1B1=C1D1.√ABCDOlA1B1C1D1O1∟∟∟∟∟5、过梯形一腰的中点且平行于底边的直线平分两条对角线及另一腰。( )√PNQ三、证明题1、已知:Rt△ABC中,∠ACB=90°,ABCD为BC边的中点,DDE⊥BC交AB于E,E求证:AB=2CE..∟∟证明:∵∠ACB=90°,∴∠BDE=∠ACB,∴DE∥CA,∵D是BC的中点,∴E是AB的中点,∴AB=2CE.∵DE⊥BC,∴∠BDE=90°;2、已知:□ABCD中,E、F分别是AB、DCABCDEF的中点,MN求证:BM=MN=NC.分析:需证明EC∥AF.证明:∵四边形ABCD是平行四边形,∴AB=DC,AB∥DC;..分别交BD于M、N,∵E、F分别是AB、DC的中点,∴AE=FC,∴四边形AECF是平行四边形,∴EC∥AF,∴BM=MN, MN=ND,即BM=MN=ND. CE、AF3、已知:梯形ABCD中,AD∥BC,ABCDEE是AB边的中点,EF∥DC,交BC于F,F求证:DC=2EF.证明:M作EM∥BC交DC于M,∵E是梯形ABCD的腰AB的中点,∴M是DC的中点,即DC=2MC;∵EF∥DC,∴EF=MC,∴DC=2EF..4、已知:直角梯形ABCD中,AD∥BC,
∠ABC=90°,ABCDEE是DC边的中点,求证:AE=BE.分析:需证E在AB的中垂线上.证明:F作EF∥BC交AB于F,∵E是梯形ABCD的腰DC的中点,∴F是AB的中点;∵EF∥BC,∠ABC=90°,∴∠AFE=∠ABC=90°,∴EF是AB的垂直平分线,∴AE=BE.∟∟.5、已知:△ABC的两中线AD、BE相交于点ABCDEGG,CH∥EB交AD的延长线于点H,H求证:AG=2GD.分析:需要证明GH=2GD=2DH.证明:∵AD、BE是中线,∴AE=EC,BD=DC,∵CH∥EB,∴AG=GH,∴AG=2GD.本题说明三角形的两中线的交点把中线分成2:1的两部分.
这个结论叫做重心定理.(现行课本已把它略去.)GD=DH,6、已知:梯形ABCD中,AD∥BC,ABCDEABDE是平行四边形,AD的延长线交EC于F,F求证:EF=FC.分析:需证明AF、BC在
其他直线上截得
相等的线段.6、已知:梯形ABCD中,AD∥BC,ABCDEABDE是平行四边形,AD的延长线交EC于F,F求证:EF=FC.分析:需证明AF、BC在
其他直线上截得
相等的线段.证法1:O连结BE交AF于点O,∵四边形ABDE是平行四边形,∵AF∥BC,∴EF=FC.∴BO=OE;″′′″ABCDEF证法2:H延长ED交BC于点H,∵四边形ABDE是平行四边形,∵AF∥BC,∴EF=FC.∴四边形ABHD是平行四边形,∴AB=DH,∴ED=DH;∴AB∥ED,即AB∥DH,且AB=ED,′′″″ABCDEF证法3:M′″″′′ABCDEF证法4:N′″″′′证法5:ABCDEFPAAS分析:本题还有多种
构造全等形的证法.
例如:证法6:AASABCDEFQ证法7:ABCDEFSAAS证法8:ABCDEFTAAS证法9:AASABCDEFP证法10:AASABCDEFQ证法11:AASABCDEFS证法12:AASABCDEFT7、已知:△ABC中,AB=AC,D在AB上,F在AC的延长线上,且BD=CF,DF交BC于E,求证:DE=EF.分析:
这是一道应已证过的题。
除用证三角形全等的方法外,
本题还可用平行线等分线段
定理的推论来证明。这里给出动画显示,证明的语句略去。证法1:ABCDEFH))((证法2:ABCDEFH(以下略去。)8、已知:AC⊥AB,DB⊥AB,O是CD的中点,求证:OA=OB.分析:需证明点O在AB的垂直平分线上.证明:作OE⊥AB于E,∵AC⊥AB,DB⊥AB,∴∠CAB=90°,∠DBA=90°,∴∠CAB=∠OEA=∠DBA,∴AC∥OE∥DB;∵O是CD的中点,∴E是AB的中点,∴OE是AB的垂直平分线,∴OA=OB.则∠OEA=90°;ABCDOE∟∟∟9、已知:AD为△ABC的中线,ABCDMPM为AD的中点,直线CM交AB于点P,求证:AP= —13AB.分析:可证明BP=2AP.证明:Q作DQ∥CP交AB于点Q;∵D是BC的中点,M是AD的中点,∴Q是BP的中点,P是AQ的中点,∴AP=PQ=QB,∴AP= —31AB.10、已知:∠ACB=90°,AC=BC,ABC求证:MN=NB.分析:
若结论成立,则过B作NC
的平行线交直线AC必截得
相等的线段,反之亦然.D∟EFMN∟∟CE=CF,EM⊥AF,CN⊥AF,ABC10、证明:D延长AC到D,使CD=CE,
连结DB.∵∠ACB=90°,CN⊥AF,∴∠CAF=∠CBD;∴∠NCF=∠CAF=∠CBD,∵EM⊥AF,∴EM∥CF,∴MN=NB.则△ACF≌△BCD,∟EFMN∟∟∴DB∥CN;∴EM∥CN∥DB,小结:
平行线等分线段定理是一个重要
的定理,在这里是利用面积证明的,
这种证法还可以用于后面即将学到的
平行线分线段成比例定理。
