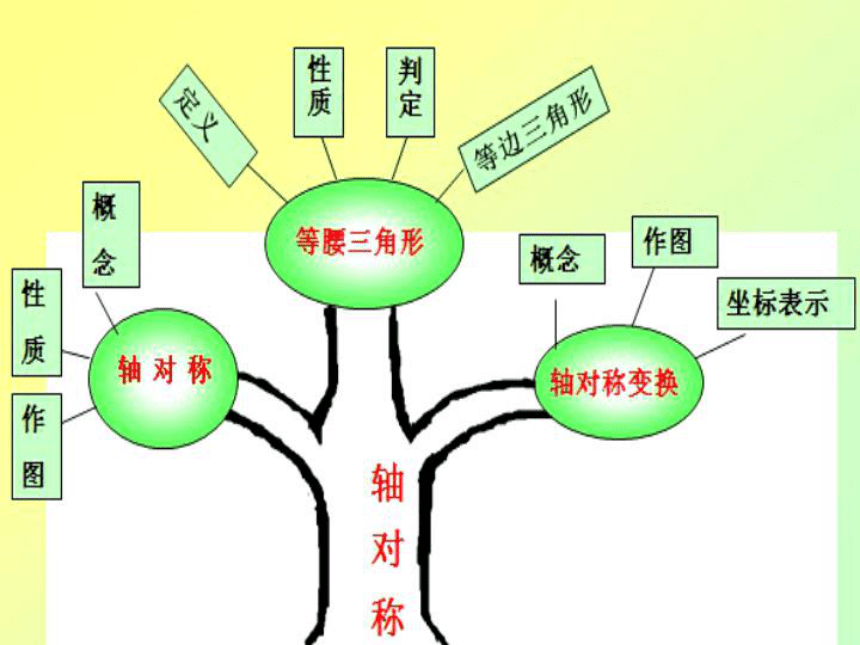
13.1轴对称
图片预览






文档简介
课件27张PPT。轴对称轴对称图形 如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形.这条直线就是它的对称轴.这时我们就说这个图形关于这条直线(或轴)对称.两个图形轴对称
把一个图形沿着某一条直线折叠,如果它能够与另一个图形重合,那么就是说这两个图形关于这条直线对称,这条直线叫做对称轴,折叠后重合的点是对应点,叫做对称点.
轴对称图形和两个图形轴对称 的区别和联系对称轴的性质
对称轴是任何一对对应点所连线段的垂直平分线.
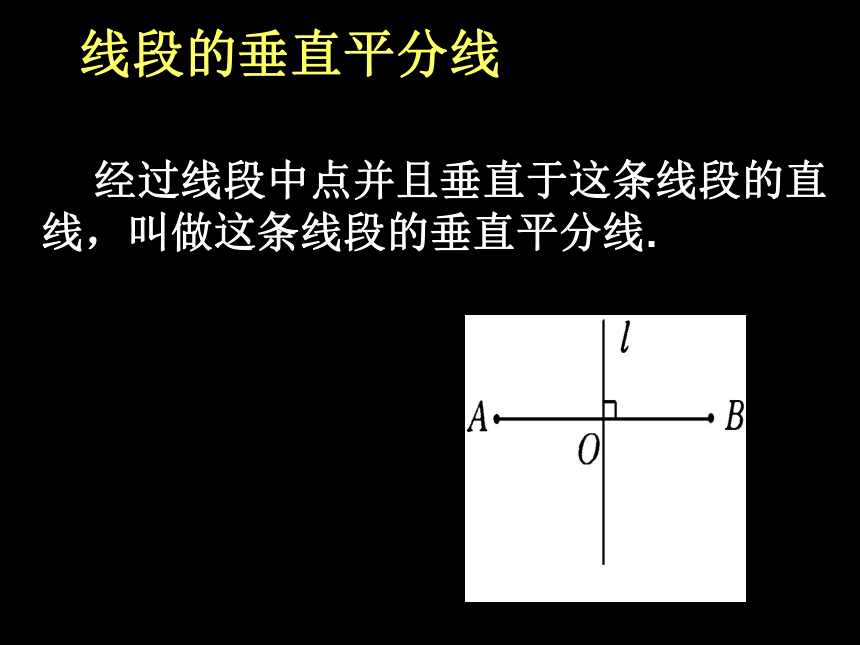
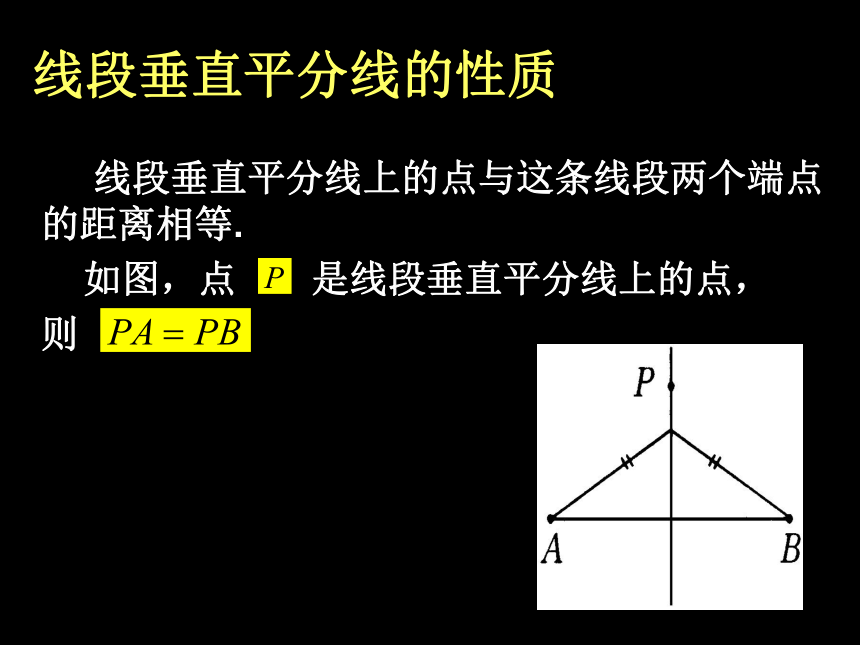
线段的垂直平分线 经过线段中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线.线段垂直平分线的性质: 线段垂直平分线上的点与这条线段两个端点的距离相等.
如图,点 是线段垂直平分线上的点,
则 线段垂直平分线的判定 与一条线段两个端点距离相等的点,在这条线段的垂直平分线上.成轴对称的两个图形 的对称轴的画法:
如果两个图形成轴对称,其对称轴就是任何一对对应点所连线段的垂直平分线.因此,我们只要找到一对对应点,作出连接它们的线段的垂直平分线,就可以得到这两个图形的对称轴.板块一
轴对称的应用例1 已知:如图,∠ABC及两点M、N。求作:点P,使得PM=PN,且P点到∠ABC两边所在的直线的距离相等。 例2 如图,三角形中,AB=AC=10cm,
作AB的垂直平分线ED交AC于D,交AB于E,量得⊿BCD的周长为17cm,请你替测量人员计算BC的长. 板块二
轴对称与几何中的最值问题 例3 如图,在公路a的同旁有两个仓库A、B,现需要建一货物中转站,要求到A、B两仓库的距离和最短,这个中转站M应建在公路旁的哪个位置比较合理? 巩固 如图,在等腰Rt⊿ABC中,CA=CB=3,E为BC上一点,满足BE=2,在斜边AB上求作一点P使得PC+PE长度之和最小。例4 如图, ∠ AOB=45°,角内有点P,在角的两边有两点Q、R(均不同于O点),求作Q、R,使得⊿PQR的周长的最小。 巩固 如图,M、N为的边AC、BC上的两个定点,在AB上求一点P,使⊿PMN的周长最短。 板块三
轴对称图形——等腰三角形例1 已知等腰三角形一腰上的高与另一腰的夹角为60°,求三角形三个内角的度数.
【巩固】已知BD是等腰⊿ ABC一腰上的高,且∠ABD=50 ° ,求⊿ ABC三个内角的度数
例 已知⊿ABC中,∠A=90 ° ∠B=67.5 °请画一条直线,把这个三角形分割成两个等腰三角形.(只需画图,不必说明理由,但要在图中标出相等两角的度数).【巩固】 在中⊿ABC中,AB=AC. 若过⊿ABC一个顶点的直线可将⊿ABC分成两个等腰三角形,求⊿ABC各内角的度数. 例 ∠MON是一个钢架, ∠MON=10 ° ,在其内部添加一些钢管BC,CD,DE,EF,FG,…添加的钢管长度都与0B相等.
⑴当添加到第五根钢管时,求∠FGM的度数.
⑵假设OM、ON足够长,能无限地添加下去吗?如果能,请说明理由.如果不能,则最多能添加几根? 如图所示,把矩形纸片ABCD沿EF折叠,使点B落在边AD上的点B’处,点A落在A’处.试说明B’E=BF
如图Rt⊿ABC中∠ACB=90 °∠A=50 °将其折叠,使点落在边上处,折痕为,则∠A’DB=____
如图,等边⊿ABC的边长为1cm,D、E分别是AB、AC上的点,将⊿ADE沿直线DE折叠,点A落在点A’处,且点A’在外部,则阴影部分图形的周长为 cm.
轴对称图形和两个图形轴对称 的区别和联系对称轴的性质
对称轴是任何一对对应点所连线段的垂直平分线.
线段的垂直平分线 经过线段中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线.线段垂直平分线的性质: 线段垂直平分线上的点与这条线段两个端点的距离相等.
如图,点 是线段垂直平分线上的点,
则 线段垂直平分线的判定 与一条线段两个端点距离相等的点,在这条线段的垂直平分线上.成轴对称的两个图形 的对称轴的画法:
如果两个图形成轴对称,其对称轴就是任何一对对应点所连线段的垂直平分线.因此,我们只要找到一对对应点,作出连接它们的线段的垂直平分线,就可以得到这两个图形的对称轴.板块一
轴对称的应用例1 已知:如图,∠ABC及两点M、N。求作:点P,使得PM=PN,且P点到∠ABC两边所在的直线的距离相等。 例2 如图,三角形中,AB=AC=10cm,
作AB的垂直平分线ED交AC于D,交AB于E,量得⊿BCD的周长为17cm,请你替测量人员计算BC的长. 板块二
轴对称与几何中的最值问题 例3 如图,在公路a的同旁有两个仓库A、B,现需要建一货物中转站,要求到A、B两仓库的距离和最短,这个中转站M应建在公路旁的哪个位置比较合理? 巩固 如图,在等腰Rt⊿ABC中,CA=CB=3,E为BC上一点,满足BE=2,在斜边AB上求作一点P使得PC+PE长度之和最小。例4 如图, ∠ AOB=45°,角内有点P,在角的两边有两点Q、R(均不同于O点),求作Q、R,使得⊿PQR的周长的最小。 巩固 如图,M、N为的边AC、BC上的两个定点,在AB上求一点P,使⊿PMN的周长最短。 板块三
轴对称图形——等腰三角形例1 已知等腰三角形一腰上的高与另一腰的夹角为60°,求三角形三个内角的度数.
【巩固】已知BD是等腰⊿ ABC一腰上的高,且∠ABD=50 ° ,求⊿ ABC三个内角的度数
例 已知⊿ABC中,∠A=90 ° ∠B=67.5 °请画一条直线,把这个三角形分割成两个等腰三角形.(只需画图,不必说明理由,但要在图中标出相等两角的度数).【巩固】 在中⊿ABC中,AB=AC. 若过⊿ABC一个顶点的直线可将⊿ABC分成两个等腰三角形,求⊿ABC各内角的度数. 例 ∠MON是一个钢架, ∠MON=10 ° ,在其内部添加一些钢管BC,CD,DE,EF,FG,…添加的钢管长度都与0B相等.
⑴当添加到第五根钢管时,求∠FGM的度数.
⑵假设OM、ON足够长,能无限地添加下去吗?如果能,请说明理由.如果不能,则最多能添加几根? 如图所示,把矩形纸片ABCD沿EF折叠,使点B落在边AD上的点B’处,点A落在A’处.试说明B’E=BF
如图Rt⊿ABC中∠ACB=90 °∠A=50 °将其折叠,使点落在边上处,折痕为,则∠A’DB=____
如图,等边⊿ABC的边长为1cm,D、E分别是AB、AC上的点,将⊿ADE沿直线DE折叠,点A落在点A’处,且点A’在外部,则阴影部分图形的周长为 cm.
