平行线性质的综合应用[下学期]
文档属性
| 名称 | 平行线性质的综合应用[下学期] |  | |
| 格式 | rar | ||
| 文件大小 | 158.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-03-18 17:27:00 | ||
图片预览

文档简介
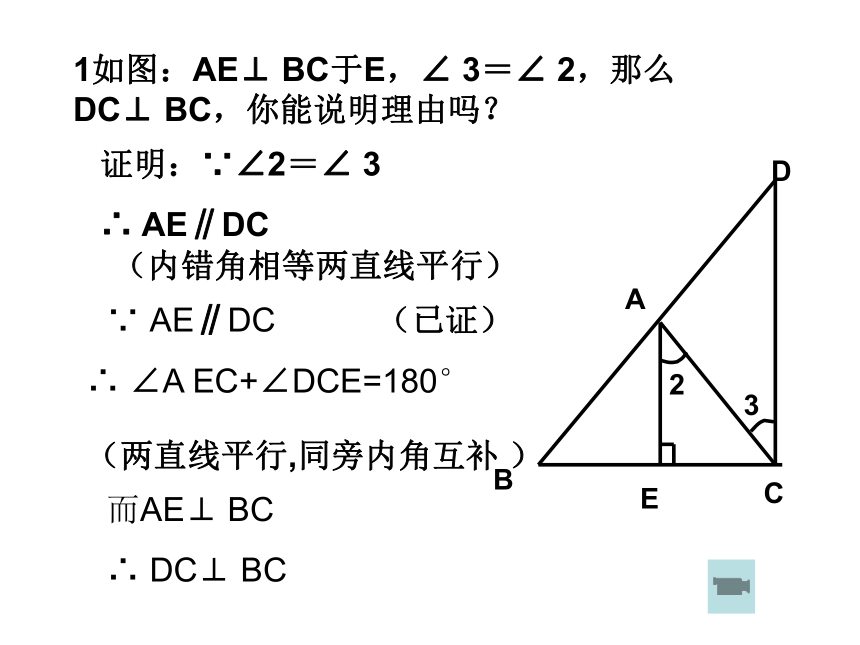
课件15张PPT。长冲中学七年级数学组平行线判定与性质综合应用1如图:AE⊥ BC于E,∠ 3=∠ 2,那么DC⊥ BC,你能说明理由吗?证明:∵∠2=∠ 3
∴ AE∥DC(内错角相等两直线平行)∵ AE∥DC(已证)∴ ∠A EC+∠DCE=180° (两直线平行,同旁内角互补 )而AE⊥ BC
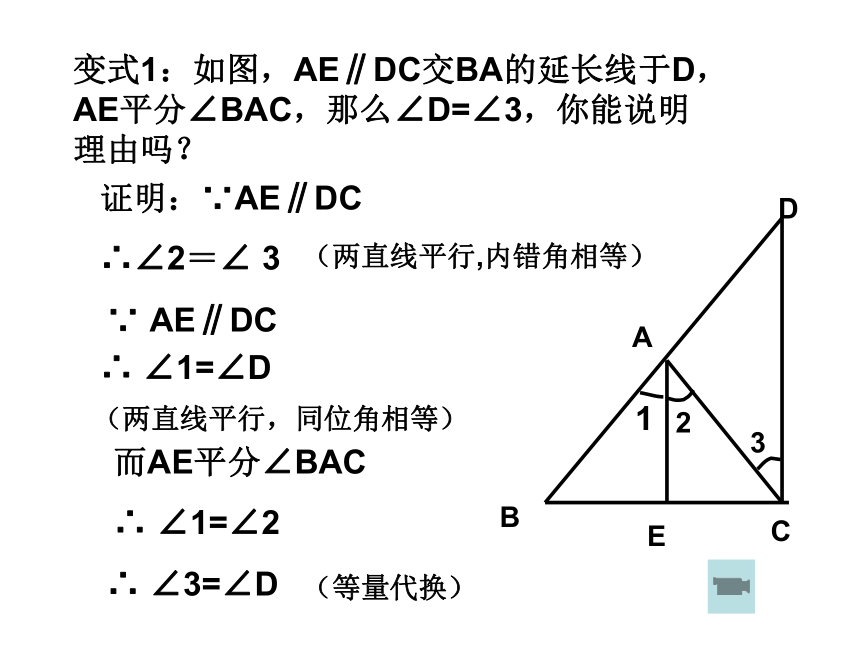
∴ DC⊥ BC变式1:如图,AE∥DC交BA的延长线于D,AE平分∠BAC,那么∠D=∠3,你能说明理由吗?证明:∵AE∥DC
∴∠2=∠ 3∵ AE∥DC∴ ∠1=∠D 而AE平分∠BAC
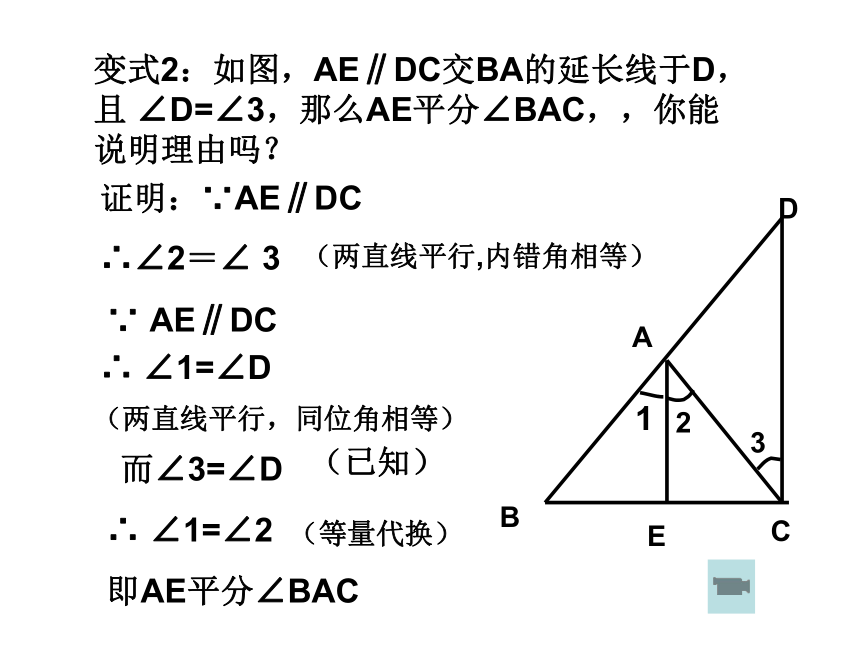
∴ ∠1=∠2(两直线平行,内错角相等)(两直线平行,同位角相等)∴ ∠3=∠D (等量代换)变式2:如图,AE∥DC交BA的延长线于D,且 ∠D=∠3,那么AE平分∠BAC,,你能说明理由吗?证明:∵AE∥DC
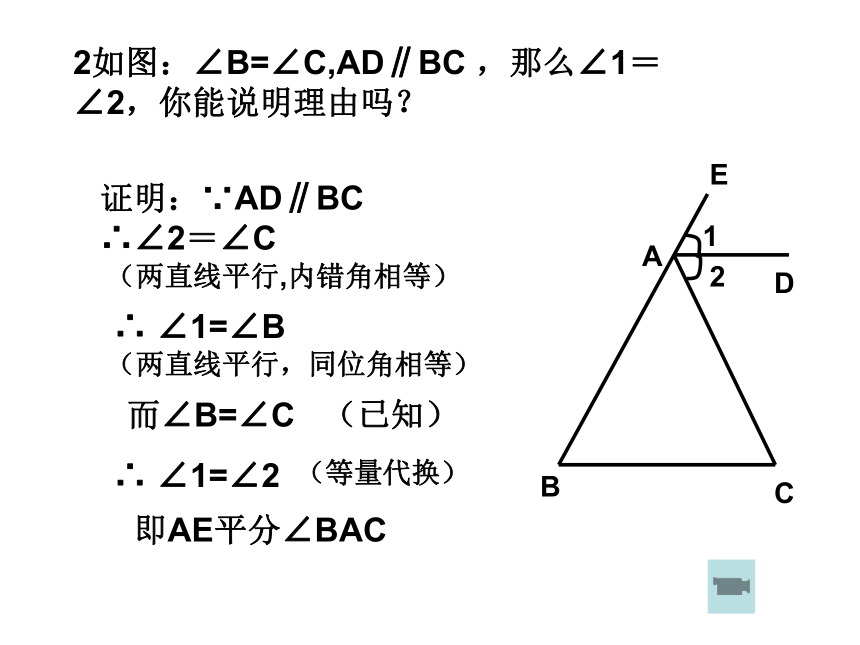
∴∠2=∠ 3∵ AE∥DC∴ ∠1=∠D 即AE平分∠BAC(两直线平行,内错角相等)(两直线平行,同位角相等)而∠3=∠D (等量代换)∴ ∠1=∠2(已知)2如图:∠B=∠C,AD∥BC ,那么∠1=∠2,你能说明理由吗?证明:∵AD∥BC
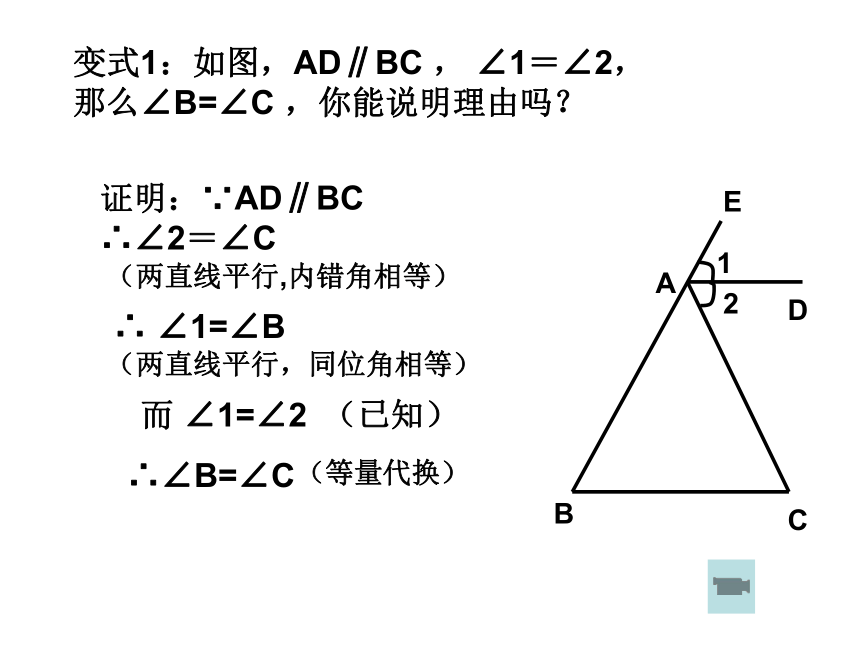
∴∠2=∠C∴ ∠1=∠B即AE平分∠BAC(两直线平行,内错角相等)(两直线平行,同位角相等)而∠B=∠C(等量代换)∴ ∠1=∠2(已知)变式1:如图,AD∥BC , ∠1=∠2,那么∠B=∠C ,你能说明理由吗?证明:∵AD∥BC
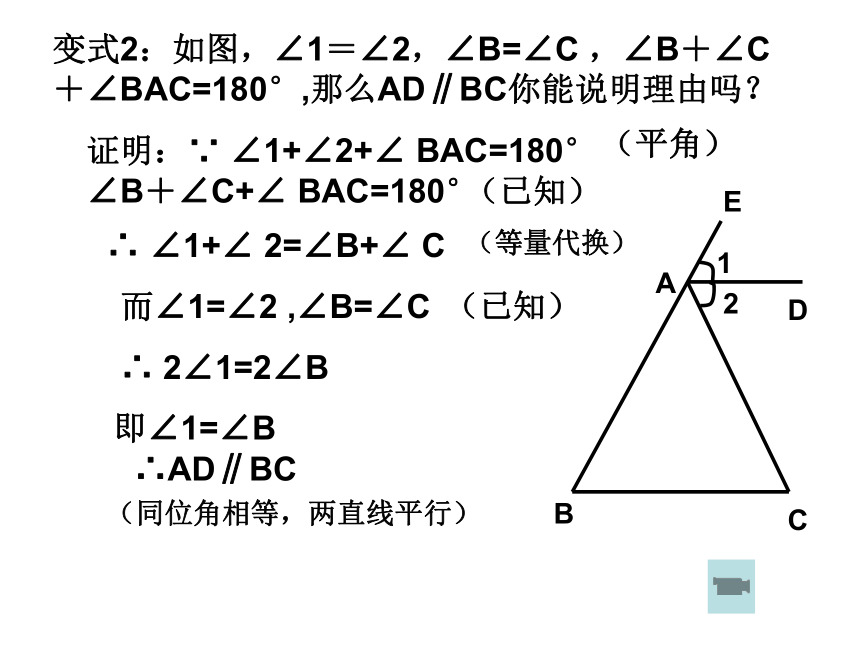
∴∠2=∠C∴ ∠1=∠B(两直线平行,内错角相等)(两直线平行,同位角相等)∴∠B=∠C(等量代换)而 ∠1=∠2(已知)变式2:如图,∠1=∠2,∠B=∠C ,∠B+∠C+∠BAC=180°,那么AD∥BC你能说明理由吗?证明:∵ ∠1+∠2+∠ BAC=180°
∠B+∠C+∠ BAC=180° ∴ ∠1+∠ 2=∠B+∠ C(同位角相等,两直线平行)(等量代换)而∠1=∠2 ,∠B=∠C(已知)(已知)(平角)∴ 2∠1=2∠B即∠1=∠B∴AD∥BC3已知:如图,AD⊥ BC于D,EG⊥ BC于G, ∠ E=∠ 3,试问:AD是∠ BAC的平分线吗?若是请说明理由。答:AD是∠ BAC的平分线∵AD⊥ BC于D,EG⊥ BC于G
∴ AD∥ EG
∴ ∠ 2=∠ 3
∠ 1=∠ E
而∠ E=∠ 3
∴ ∠ 1=∠ 2
即:AD是∠ BAC的平分线(同时垂直于一条直线的两条直线互相平行)(两直线平行内错角相等,同位角相等)3已知:如图,∠ 1与∠ 2互补,∠ D=∠B,那么∠ A=∠ C,请说明理由。证明:∵∠ 1+∠2=180°
∴ DF∥ HB(同旁内角互补,两直线平行)∴∠ B=∠ 3 (两直线平行,同位角相等)而∠ B=∠ D
∴∠ 3=∠ D (等量代换)∴AB∥ CD (内错角相等,量直线平行)∴ ∠ A=∠ C(两直线平行,内错角相等)变式1:已知,如图, ∠ A=∠ C ,∠ D=∠B,那么∠ 1与∠ 2互补请说明理由。 ∴ DF∥ HB∴∠ B=∠ 3 ∴∠ 3=∠ D 而∠ B=∠ D(等量代换)∴AB∥ CD (内错角相等,两直线平行)证明:∵ ∠ A=∠ C(两直线平行,内错角相等)(同位角相等,两直线平行) ∴ ∠ 1+∠2=180°(两直线平行,同旁内角互补) 4已知:如图,AB∥CD,分别探讨下列四个图形中∠APC与∠PAB, ∠PCD的关系,请以所得的四个关系式中任选一个加以说明。位置1:∠ PAB+∠ PCD+∠ APC=360° 结论:位置2:∠ PAB+∠ PCD=∠ APC 位置3:∠ PCD -∠ PAB =∠ APC 位置4:∠ PAB - ∠ PCD =∠ APC 在图1中:过P作PE∥ CD
而AB∥ CD,所以AB∥ PE∥ CD(如果一条直线平行于两平行线中的一条直线,那么这三条直线互相平行)∴ ∠ 1+∠ A=180°
∠ 2+∠ C=180°(两直线平行,同旁内角互补)∴ ∠ 1+∠ 2+∠ A+∠ C=360° 即:∠ PAB+∠ PCD+∠ APC=360° 在图2中:过P作PE∥ CD
而AB∥ CD,所以AB∥ PE∥ CD(如果一条直线平行于两平行线中的一条直线,那么这三条直线互相平行)∴ ∠ 1=∠A
∠ 2=∠ C(两直线平行,内错角相等)∴ ∠ 1+∠ 2=∠ A+∠ C 即:∠ PAB+∠ PCD=∠ APC 在图3中:(如果一条直线平行于两平行线中的一条直线,那么这三条直线互相平行)∵∠ 1=∠A
∠ 2=∠ C(两直线平行,内错角相等)∠ 2- ∠ 1 =∠ C -∠ A即:∠ PCD -∠ PAB =∠ APC 过P作PE∥ CD
而AB∥ CD,所以AB∥ PE∥ CD
∴ AE∥DC(内错角相等两直线平行)∵ AE∥DC(已证)∴ ∠A EC+∠DCE=180° (两直线平行,同旁内角互补 )而AE⊥ BC
∴ DC⊥ BC变式1:如图,AE∥DC交BA的延长线于D,AE平分∠BAC,那么∠D=∠3,你能说明理由吗?证明:∵AE∥DC
∴∠2=∠ 3∵ AE∥DC∴ ∠1=∠D 而AE平分∠BAC
∴ ∠1=∠2(两直线平行,内错角相等)(两直线平行,同位角相等)∴ ∠3=∠D (等量代换)变式2:如图,AE∥DC交BA的延长线于D,且 ∠D=∠3,那么AE平分∠BAC,,你能说明理由吗?证明:∵AE∥DC
∴∠2=∠ 3∵ AE∥DC∴ ∠1=∠D 即AE平分∠BAC(两直线平行,内错角相等)(两直线平行,同位角相等)而∠3=∠D (等量代换)∴ ∠1=∠2(已知)2如图:∠B=∠C,AD∥BC ,那么∠1=∠2,你能说明理由吗?证明:∵AD∥BC
∴∠2=∠C∴ ∠1=∠B即AE平分∠BAC(两直线平行,内错角相等)(两直线平行,同位角相等)而∠B=∠C(等量代换)∴ ∠1=∠2(已知)变式1:如图,AD∥BC , ∠1=∠2,那么∠B=∠C ,你能说明理由吗?证明:∵AD∥BC
∴∠2=∠C∴ ∠1=∠B(两直线平行,内错角相等)(两直线平行,同位角相等)∴∠B=∠C(等量代换)而 ∠1=∠2(已知)变式2:如图,∠1=∠2,∠B=∠C ,∠B+∠C+∠BAC=180°,那么AD∥BC你能说明理由吗?证明:∵ ∠1+∠2+∠ BAC=180°
∠B+∠C+∠ BAC=180° ∴ ∠1+∠ 2=∠B+∠ C(同位角相等,两直线平行)(等量代换)而∠1=∠2 ,∠B=∠C(已知)(已知)(平角)∴ 2∠1=2∠B即∠1=∠B∴AD∥BC3已知:如图,AD⊥ BC于D,EG⊥ BC于G, ∠ E=∠ 3,试问:AD是∠ BAC的平分线吗?若是请说明理由。答:AD是∠ BAC的平分线∵AD⊥ BC于D,EG⊥ BC于G
∴ AD∥ EG
∴ ∠ 2=∠ 3
∠ 1=∠ E
而∠ E=∠ 3
∴ ∠ 1=∠ 2
即:AD是∠ BAC的平分线(同时垂直于一条直线的两条直线互相平行)(两直线平行内错角相等,同位角相等)3已知:如图,∠ 1与∠ 2互补,∠ D=∠B,那么∠ A=∠ C,请说明理由。证明:∵∠ 1+∠2=180°
∴ DF∥ HB(同旁内角互补,两直线平行)∴∠ B=∠ 3 (两直线平行,同位角相等)而∠ B=∠ D
∴∠ 3=∠ D (等量代换)∴AB∥ CD (内错角相等,量直线平行)∴ ∠ A=∠ C(两直线平行,内错角相等)变式1:已知,如图, ∠ A=∠ C ,∠ D=∠B,那么∠ 1与∠ 2互补请说明理由。 ∴ DF∥ HB∴∠ B=∠ 3 ∴∠ 3=∠ D 而∠ B=∠ D(等量代换)∴AB∥ CD (内错角相等,两直线平行)证明:∵ ∠ A=∠ C(两直线平行,内错角相等)(同位角相等,两直线平行) ∴ ∠ 1+∠2=180°(两直线平行,同旁内角互补) 4已知:如图,AB∥CD,分别探讨下列四个图形中∠APC与∠PAB, ∠PCD的关系,请以所得的四个关系式中任选一个加以说明。位置1:∠ PAB+∠ PCD+∠ APC=360° 结论:位置2:∠ PAB+∠ PCD=∠ APC 位置3:∠ PCD -∠ PAB =∠ APC 位置4:∠ PAB - ∠ PCD =∠ APC 在图1中:过P作PE∥ CD
而AB∥ CD,所以AB∥ PE∥ CD(如果一条直线平行于两平行线中的一条直线,那么这三条直线互相平行)∴ ∠ 1+∠ A=180°
∠ 2+∠ C=180°(两直线平行,同旁内角互补)∴ ∠ 1+∠ 2+∠ A+∠ C=360° 即:∠ PAB+∠ PCD+∠ APC=360° 在图2中:过P作PE∥ CD
而AB∥ CD,所以AB∥ PE∥ CD(如果一条直线平行于两平行线中的一条直线,那么这三条直线互相平行)∴ ∠ 1=∠A
∠ 2=∠ C(两直线平行,内错角相等)∴ ∠ 1+∠ 2=∠ A+∠ C 即:∠ PAB+∠ PCD=∠ APC 在图3中:(如果一条直线平行于两平行线中的一条直线,那么这三条直线互相平行)∵∠ 1=∠A
∠ 2=∠ C(两直线平行,内错角相等)∠ 2- ∠ 1 =∠ C -∠ A即:∠ PCD -∠ PAB =∠ APC 过P作PE∥ CD
而AB∥ CD,所以AB∥ PE∥ CD
