4.5 函数的应用 测试题(含解析)
文档属性
| 名称 | 4.5 函数的应用 测试题(含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 161.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-09 10:11:48 | ||
图片预览




文档简介
函数的应用 测试题
(时间120分钟 满分150分)
班级 学号 姓名 得分
第Ⅰ卷 (选择题 共60分)
一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1、设g(x)=3x+3x-8,用二分法求方程3x+3x-8=0在x∈(1,2)内近似解的过程中得g(1.5)>0,g(1.25)<0,则方程的根落在区间( )
A.(1,1.25) B.(1.25,1.5)
C.(1.5,2) D.不确定
2、函数f(x)=x2-2x-3的零点是( )
A.1,-3 B.3,-1 C.1,2 D.不存在
3、下列函数中,不能用二分法求零点的是( )
A.y=3x+1 B.y=x2-1
C.y=log2(x-1) D.y=(x-1)2
4、某种品牌的自行车自投放市场以来,经过两次降价,单价由原来的2 000元降到1 280元,则这种自行车的价格平均每次降低的百分率是( )
A.10% B.15% C.18% D.20%
5、函数f(x)=ln(x+1)-的零点所在的大致区间是( )
A.(0,1) B.(1,2) C.(2,e) D.(3,4)
6、设函数f(x)=若f(-4)=f(0),f(-2)=-2,则函数y=f(x)-x的零点的个数为( )
A.1 B.2 C.3 D.4
7、若函数y=|1-x|+m的图象与x轴有公共点,则m的取值范围是( )
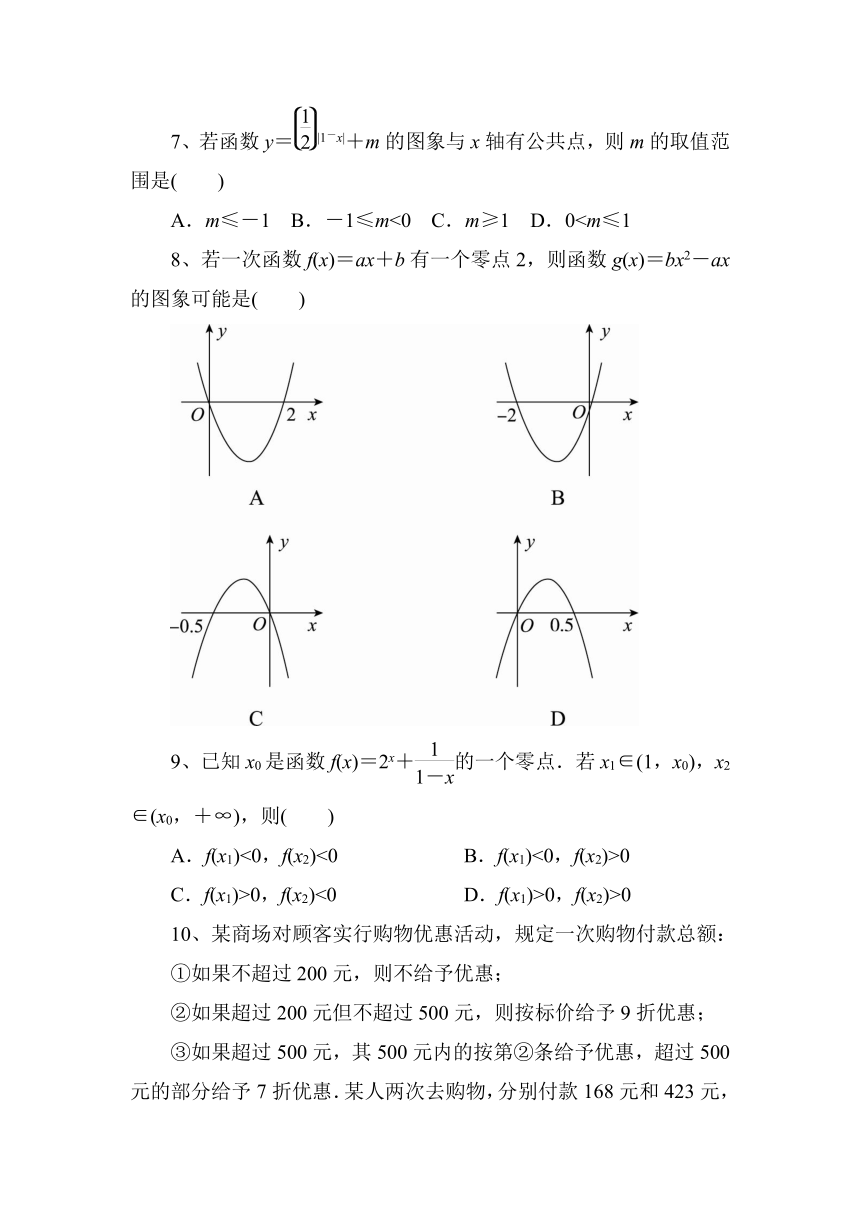
A.m≤-1 B.-1≤m<0 C.m≥1 D.08、若一次函数f(x)=ax+b有一个零点2,则函数g(x)=bx2-ax的图象可能是( )
9、已知x0是函数f(x)=2x+的一个零点.若x1∈(1,x0),x2∈(x0,+∞),则( )
A.f(x1)<0,f(x2)<0 B.f(x1)<0,f(x2)>0
C.f(x1)>0,f(x2)<0 D.f(x1)>0,f(x2)>0
10、某商场对顾客实行购物优惠活动,规定一次购物付款总额:
①如果不超过200元,则不给予优惠;
②如果超过200元但不超过500元,则按标价给予9折优惠;
③如果超过500元,其500元内的按第②条给予优惠,超过500元的部分给予7折优惠.某人两次去购物,分别付款168元和423元,假设他一次性购买上述两次同样的商品,则应付款( )
A.413.7元 B.513.7元
C.546.6元 D.548.7元
11、已知0A.2 B.3 C.4 D.与a的值有关
12、若对于定义在R上的函数f(x),其图象是连续的,且存在常数λ(λ∈R),使得f(x+λ)+λf(x)=0对任意的实数x成立,则称f(x)是“λ-同伴函数”.下列关于“λ-同伴函数”的叙述中正确的是( )
A.“-同伴函数”至少有一个零点
B.f(x)=x2是一个“λ-同伴函数”
C.f(x)=log2x是一个“λ-同伴函数”
D.f(x)=0是唯一一个常值“λ-同伴函数”
第Ⅱ卷 (非选择题 共90分)
二、填空题(本大题共4个小题,每小题5分,共20分,请把正确答案填在题中横线上)
13、函数g(x)=x2+mx-6的一个零点是-6,则另一个零点是________.
14、根据表格中的数据,若函数f(x)=ln x-x+2在区间(k,k+1)(k∈N*)内有一个零点,则k的值为________.
x 1 2 3 4 5
ln x 0 0.69 1.10 1.39 1.61
15、某市出租车收费标准如下:起步价为8元,起步里程为3 km(不超过3 km按起步价付费);超过3 km但不超过8 km时,超过部分按每千米2.15元收费;超过8 km时,超过部分按每千米2.85元收费,另每次乘坐需付燃油附加费1元.现某人乘坐一次出租车付费22.6元,则此次出租车行驶的路程为________km.
16、设定义域为R的函数f(x)=若关于x的方程[2f(x)]2-(2a+3)f(x)+3a=0有五个不同的实数解,则a的取值范围是________.
三、解答题(本大题共6个小题,共70分,解答时应写出必要的文字说明、证明过程或演算步骤)
17、(本小题满分10分)
已知二次函数g(x)的图象过点(0,3),它的图象的对称轴为x=2,且g(x)的两个零点的平方和为10,求g(x)的解析式.
18、(本小题满分12分)
某公司制定了一个激励销售人员的奖励方案:当销售利润不超过10万元时,按销售利润的15%进行奖励;当销售利润超过10万元时,若超出A万元,则超出部分按2log5(A+1)进行奖励.记奖金为y(单位:万元),销售利润为x(单位:万元).
(1)写出该公司激励销售人员的奖励方案的函数模型;
(2)如果业务员老江获得5.5万元的奖金,那么他的销售利润是多少万元?
19、(本小题满分12分)
已知定义在R上奇函数f(x)在x≥0时的图象是如图所示的抛物线的一部分.
(1)请补全函数f(x)的图象;
(2)写出函数f(x)的表达式(只写明结果,无需过程);
(3)讨论方程|f(x)|=a的解的个数(只写明结果,无需过程).
20、(本小题满分12分)
函数y=f(x)的图象关于x=1对称,当x≤1时,f(x)=x2-1.
(1)写出y=f(x)的解析式并作出图象;
(2)根据图象讨论f(x)-a=0(a∈R)的根的情况.
21、(本小题满分12分)
已知函数g(x)=log4(4x+1)+mx,(k∈R)为偶函数.
(1)求m的值;
(2)若函数g(x)=log4(a·2x-a)有且仅有一个根,求实数a的取值范围.
22、.(本小题满分12分)
一位小伙子进行理财投资,根据长期收益率市场预测,投资债券等稳健型产品的收益与投资额成正比,投资股票等风险型产品的收益与投资额的算术平方根成正比.已知投资1万元时两类产品的收益分别为0.125万元和0.5万元(如图).
(1)分别写出两种产品的收益与投资的函数关系;
(2)这位小伙子有20万元资金,全部用于理财投资,问:怎么分配资金能使投资获得最大收益,其最大收益是多少万元?
答案解析
B 解析:因为g(1.5)>0,g(1.25)<0,所以由零点存在性定理可得,方程3x+3x-8=0的根落在区间(1.25,1.5)内.
B 解析:令x2-2x-3=0得x=-1或x=3,故选B
D 解析:结合函数y=(x-1)2的图象可知,该函数在x=1的左右两侧函数值的符号均为正,故其不能用二分法求零点.
D 解析:由题意,可设平均每次价格降低的百分率为x,
则有2 000(1-x)2=1 280,
解得x=0.2或x=1.8(舍去),故选D.
B 解析:f(1)=ln(1+1)-=ln 2-2=ln 2-ln e2<0,f(2)=ln(2+1)-=ln 3-1>0,因此函数的零点必在区间(1,2)内,故选B.
C 解析:本题主要考查二次函数、分段函数及函数的零点.f(-4)=f(0) b=4,f(-2)=-2 c=2,∴ f(x)=当x≤0时,由x2+4x+2=x解得x1=-1,x2=-2;当x>0时,x=3.所以函数y=f(x)-x的零点的个数为3,故选C.
B 解析:函数图象与x轴有公共点,即函数
f(x)=|1-x|,g(x)=-m有交点.作出f(x),g(x)的图象,如图所示.
0<-m≤1,即-1≤m<0,故选B.
C 解析:由题意知,2a+b=0,所以a=-.
因此g(x)=bx2+x=b=b2-.
易知函数g(x)图象的对称轴为x=-,排除A,D.
又令g(x)=0,得x=0或x=-0.5,故选C.
B 解析:由定义法证明函数的单调性的方法,得f(x)在(1,+∞)上为增函数,又1解题技巧:本题主要考查了函数的零点和单调性,解决本题的关键是判断出函数f(x)=2x+的单调性.
C 解析:设该顾客两次购物的商品价格分别为x,y元,由题意可知x=168,y×0.9=423,∴y=470,故x+y=168+470=638(元),
故如果他一次性购买上述两样商品应付款:
(638-500)×0.7+500×0.9=96.6+450=546.6(元).
A 解析:设y1=a|x|,y2=|logax|,分别作出它们的图象如下图所示.
由图可知,有两个交点,故方程a|x|=|logax|有两个根.故选A.
A 解析:令x=0,得f+f(0)=0,所以f=-f(0).若f(0)=0,显然f(x)=0有实数根;若f(0)≠0,f·f(0)=-(f(0))2<0.又因为函数f(x)的图象是连续不断的,所以f(x)=0在上必有实数根,即任意“-同伴函数”至少有一个零点.故A正确;
用反证法,假设f(x)=x2是一个“λ-同伴函数”,则(x+λ)2+λx2=0,即(1+λ)x2+2λx+λ2=0对任意实数x成立,所以λ+1=2λ=λ2=0,而此式无解,所以f(x)=x2不是一个“λ-同伴函数”.故B错误;
因为f(x)=log2x的定义域不是R.故C错误;
设f(x)=C是一个“λ-同伴函数”,则(1+λ)C=0,当λ=-1时,可以取遍实数集,因此f(x)=0不是唯一一个常值“λ-同伴函数”.故D错误.
1 解析:依题意可知,g(-6)=(-6)2-6m-6=0 m=5,所以g(x)=x2+5x-6=(x+6)(x-1),令g(x)=0,解得x=-6或x=1,所以另一个零点是1.
3 解析:由表中数据可知,f(1)=ln 1-1+2=1>0,
f(2)=ln 2-2+2=ln 2=0.69>0,
f(3)=ln 3-3+2=1.10-1=0.1>0,
f(4)=ln 4-4+2=1.39-2=-0.61<0,
f(5)=ln 5-5+2=1.61-3=-1.39<0,
∴f(3)·f(4)<0,∴k的值为3.
9 解析:设乘客每次乘坐出租车需付费用为f(x)元,由题意,得
f(x)=
令f(x)=22.6,显然9+5×2.15+(x-8)×2.85=22.6(x>8),解得x=9.
1<a<或∴要求对应于f(x)等于某个常数有3个不同实数解,
∴先根据题意作出f(x)的简图:
由图可知,只有当f(x)=a时,它有三个根.
所以有1<a<2①.
再根据2f(x)2-(2a+3)f(x)+3a=0有两个不等实根,
得:Δ>0即(2a+3)2-24a>0,a≠②.
结合①②得:1<a<或解题技巧:本题主要考查了函数零点和方程解的关系,解决本题的关键是找出隐含条件f(x)=a有3个不同实数解.
解:设g(x)=ax2+bx+c(a≠0),
由题意知,c=3,-=2.
设x1,x2是方程ax2+bx+c=0的两根,
则x1+x2=-,x1·x2=.
∵x+x=10,∴(x1+x2)2-2x1x2=10,
即2-=10,∴42-=10,
∴a=1,b=-4.
∴g(x)=x2-4x+3.
解:(1)由题意,得
y=
(2)x∈(0,10],0.15x≤1.5.
又∵y=5.5,∴x>10,
∴1.5+2log5(x-9)=5.5,∴x=34.
∴老江的销售利润是34万元.
解:(1)补全f(x)的图象如图①所示.
①
(2)当x≥0时,设f(x)=a(x-1)2-2,由f(0)=0得,a=2,
所以此时,f(x)=2(x-1)2-2,即f(x)=2x2-4x,
当x<0时,-x>0,
所以f(-x)=2(-x)2-4(-x)=2x2+4x,①
又f(-x)=-f(x),代入①,得f(x)=-2x2-4x,
所以f(x)=
(3)函数y=|f(x)|的图象如图②所示.
②
由图可知,当a<0时,方程无解;
当a=0时,方程有三个解;
当0当a=2时,方程有4个解;
当a>2时,方程有2个解.
20、解:(1)由题意知f(x)=
图象如图所示.
(2)当a<-1时,f(x)-a=0无解;
当a=-1时,f(x)-a=0有两个实数根;
当-1当a=0时,f(x)-a=0有三个实数根;
当a>0时,f(x)-a=0有两个实数根.
21、解:(1)∵g(x)为偶函数,∴g(-x)=g(x),
即log4(4-x+1)-mx=log4(4x+1)+mx,
∴log4-log4(4x+1)=2mx,
∴(2m+1)x=0,∴m=-.
(2)依题意知,log4(4x+1)-x=log4(a·2x-a),
整理,得log4(4x+1)=log4 [(a·2x-a)2x],
∴4x+1=(a·2x-a)·2x(*).
令t=2x,则(*)变为(1-a)t2+at+1=0(**)只需其仅有一正根.
①当a=1时,t=-1不合题意;
②当(**)式有一正一负根时,∴得a>1;
③当(**)式有两相等的正根时,Δ=0,∴a=±2-2,且>0,
∴a=-2-2.
综上所述,a的取值范围为{a|a>1或a=-2-2}.
22、解:(1)设f(x)=k1x,g(x)=k2,
所以f(1)==k1,
g(1)==k2,即f(x)=x(x≥0),g(x)=(x≥0).
(2)设投资债券类产品x万元,则股票类投资为(20-x)万元.
依题意,得
y=f(x)+g(20-x)
=+(0≤x≤20).
令t=(0≤t≤2).
则y=+t=-(t-2)2+3,
所以当t=2,即x=16(万元)时,收益最大,最大收益为3万元.
(时间120分钟 满分150分)
班级 学号 姓名 得分
第Ⅰ卷 (选择题 共60分)
一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1、设g(x)=3x+3x-8,用二分法求方程3x+3x-8=0在x∈(1,2)内近似解的过程中得g(1.5)>0,g(1.25)<0,则方程的根落在区间( )
A.(1,1.25) B.(1.25,1.5)
C.(1.5,2) D.不确定
2、函数f(x)=x2-2x-3的零点是( )
A.1,-3 B.3,-1 C.1,2 D.不存在
3、下列函数中,不能用二分法求零点的是( )
A.y=3x+1 B.y=x2-1
C.y=log2(x-1) D.y=(x-1)2
4、某种品牌的自行车自投放市场以来,经过两次降价,单价由原来的2 000元降到1 280元,则这种自行车的价格平均每次降低的百分率是( )
A.10% B.15% C.18% D.20%
5、函数f(x)=ln(x+1)-的零点所在的大致区间是( )
A.(0,1) B.(1,2) C.(2,e) D.(3,4)
6、设函数f(x)=若f(-4)=f(0),f(-2)=-2,则函数y=f(x)-x的零点的个数为( )
A.1 B.2 C.3 D.4
7、若函数y=|1-x|+m的图象与x轴有公共点,则m的取值范围是( )
A.m≤-1 B.-1≤m<0 C.m≥1 D.0
9、已知x0是函数f(x)=2x+的一个零点.若x1∈(1,x0),x2∈(x0,+∞),则( )
A.f(x1)<0,f(x2)<0 B.f(x1)<0,f(x2)>0
C.f(x1)>0,f(x2)<0 D.f(x1)>0,f(x2)>0
10、某商场对顾客实行购物优惠活动,规定一次购物付款总额:
①如果不超过200元,则不给予优惠;
②如果超过200元但不超过500元,则按标价给予9折优惠;
③如果超过500元,其500元内的按第②条给予优惠,超过500元的部分给予7折优惠.某人两次去购物,分别付款168元和423元,假设他一次性购买上述两次同样的商品,则应付款( )
A.413.7元 B.513.7元
C.546.6元 D.548.7元
11、已知0
12、若对于定义在R上的函数f(x),其图象是连续的,且存在常数λ(λ∈R),使得f(x+λ)+λf(x)=0对任意的实数x成立,则称f(x)是“λ-同伴函数”.下列关于“λ-同伴函数”的叙述中正确的是( )
A.“-同伴函数”至少有一个零点
B.f(x)=x2是一个“λ-同伴函数”
C.f(x)=log2x是一个“λ-同伴函数”
D.f(x)=0是唯一一个常值“λ-同伴函数”
第Ⅱ卷 (非选择题 共90分)
二、填空题(本大题共4个小题,每小题5分,共20分,请把正确答案填在题中横线上)
13、函数g(x)=x2+mx-6的一个零点是-6,则另一个零点是________.
14、根据表格中的数据,若函数f(x)=ln x-x+2在区间(k,k+1)(k∈N*)内有一个零点,则k的值为________.
x 1 2 3 4 5
ln x 0 0.69 1.10 1.39 1.61
15、某市出租车收费标准如下:起步价为8元,起步里程为3 km(不超过3 km按起步价付费);超过3 km但不超过8 km时,超过部分按每千米2.15元收费;超过8 km时,超过部分按每千米2.85元收费,另每次乘坐需付燃油附加费1元.现某人乘坐一次出租车付费22.6元,则此次出租车行驶的路程为________km.
16、设定义域为R的函数f(x)=若关于x的方程[2f(x)]2-(2a+3)f(x)+3a=0有五个不同的实数解,则a的取值范围是________.
三、解答题(本大题共6个小题,共70分,解答时应写出必要的文字说明、证明过程或演算步骤)
17、(本小题满分10分)
已知二次函数g(x)的图象过点(0,3),它的图象的对称轴为x=2,且g(x)的两个零点的平方和为10,求g(x)的解析式.
18、(本小题满分12分)
某公司制定了一个激励销售人员的奖励方案:当销售利润不超过10万元时,按销售利润的15%进行奖励;当销售利润超过10万元时,若超出A万元,则超出部分按2log5(A+1)进行奖励.记奖金为y(单位:万元),销售利润为x(单位:万元).
(1)写出该公司激励销售人员的奖励方案的函数模型;
(2)如果业务员老江获得5.5万元的奖金,那么他的销售利润是多少万元?
19、(本小题满分12分)
已知定义在R上奇函数f(x)在x≥0时的图象是如图所示的抛物线的一部分.
(1)请补全函数f(x)的图象;
(2)写出函数f(x)的表达式(只写明结果,无需过程);
(3)讨论方程|f(x)|=a的解的个数(只写明结果,无需过程).
20、(本小题满分12分)
函数y=f(x)的图象关于x=1对称,当x≤1时,f(x)=x2-1.
(1)写出y=f(x)的解析式并作出图象;
(2)根据图象讨论f(x)-a=0(a∈R)的根的情况.
21、(本小题满分12分)
已知函数g(x)=log4(4x+1)+mx,(k∈R)为偶函数.
(1)求m的值;
(2)若函数g(x)=log4(a·2x-a)有且仅有一个根,求实数a的取值范围.
22、.(本小题满分12分)
一位小伙子进行理财投资,根据长期收益率市场预测,投资债券等稳健型产品的收益与投资额成正比,投资股票等风险型产品的收益与投资额的算术平方根成正比.已知投资1万元时两类产品的收益分别为0.125万元和0.5万元(如图).
(1)分别写出两种产品的收益与投资的函数关系;
(2)这位小伙子有20万元资金,全部用于理财投资,问:怎么分配资金能使投资获得最大收益,其最大收益是多少万元?
答案解析
B 解析:因为g(1.5)>0,g(1.25)<0,所以由零点存在性定理可得,方程3x+3x-8=0的根落在区间(1.25,1.5)内.
B 解析:令x2-2x-3=0得x=-1或x=3,故选B
D 解析:结合函数y=(x-1)2的图象可知,该函数在x=1的左右两侧函数值的符号均为正,故其不能用二分法求零点.
D 解析:由题意,可设平均每次价格降低的百分率为x,
则有2 000(1-x)2=1 280,
解得x=0.2或x=1.8(舍去),故选D.
B 解析:f(1)=ln(1+1)-=ln 2-2=ln 2-ln e2<0,f(2)=ln(2+1)-=ln 3-1>0,因此函数的零点必在区间(1,2)内,故选B.
C 解析:本题主要考查二次函数、分段函数及函数的零点.f(-4)=f(0) b=4,f(-2)=-2 c=2,∴ f(x)=当x≤0时,由x2+4x+2=x解得x1=-1,x2=-2;当x>0时,x=3.所以函数y=f(x)-x的零点的个数为3,故选C.
B 解析:函数图象与x轴有公共点,即函数
f(x)=|1-x|,g(x)=-m有交点.作出f(x),g(x)的图象,如图所示.
0<-m≤1,即-1≤m<0,故选B.
C 解析:由题意知,2a+b=0,所以a=-.
因此g(x)=bx2+x=b=b2-.
易知函数g(x)图象的对称轴为x=-,排除A,D.
又令g(x)=0,得x=0或x=-0.5,故选C.
B 解析:由定义法证明函数的单调性的方法,得f(x)在(1,+∞)上为增函数,又1
C 解析:设该顾客两次购物的商品价格分别为x,y元,由题意可知x=168,y×0.9=423,∴y=470,故x+y=168+470=638(元),
故如果他一次性购买上述两样商品应付款:
(638-500)×0.7+500×0.9=96.6+450=546.6(元).
A 解析:设y1=a|x|,y2=|logax|,分别作出它们的图象如下图所示.
由图可知,有两个交点,故方程a|x|=|logax|有两个根.故选A.
A 解析:令x=0,得f+f(0)=0,所以f=-f(0).若f(0)=0,显然f(x)=0有实数根;若f(0)≠0,f·f(0)=-(f(0))2<0.又因为函数f(x)的图象是连续不断的,所以f(x)=0在上必有实数根,即任意“-同伴函数”至少有一个零点.故A正确;
用反证法,假设f(x)=x2是一个“λ-同伴函数”,则(x+λ)2+λx2=0,即(1+λ)x2+2λx+λ2=0对任意实数x成立,所以λ+1=2λ=λ2=0,而此式无解,所以f(x)=x2不是一个“λ-同伴函数”.故B错误;
因为f(x)=log2x的定义域不是R.故C错误;
设f(x)=C是一个“λ-同伴函数”,则(1+λ)C=0,当λ=-1时,可以取遍实数集,因此f(x)=0不是唯一一个常值“λ-同伴函数”.故D错误.
1 解析:依题意可知,g(-6)=(-6)2-6m-6=0 m=5,所以g(x)=x2+5x-6=(x+6)(x-1),令g(x)=0,解得x=-6或x=1,所以另一个零点是1.
3 解析:由表中数据可知,f(1)=ln 1-1+2=1>0,
f(2)=ln 2-2+2=ln 2=0.69>0,
f(3)=ln 3-3+2=1.10-1=0.1>0,
f(4)=ln 4-4+2=1.39-2=-0.61<0,
f(5)=ln 5-5+2=1.61-3=-1.39<0,
∴f(3)·f(4)<0,∴k的值为3.
9 解析:设乘客每次乘坐出租车需付费用为f(x)元,由题意,得
f(x)=
令f(x)=22.6,显然9+5×2.15+(x-8)×2.85=22.6(x>8),解得x=9.
1<a<或
∴先根据题意作出f(x)的简图:
由图可知,只有当f(x)=a时,它有三个根.
所以有1<a<2①.
再根据2f(x)2-(2a+3)f(x)+3a=0有两个不等实根,
得:Δ>0即(2a+3)2-24a>0,a≠②.
结合①②得:1<a<或
解:设g(x)=ax2+bx+c(a≠0),
由题意知,c=3,-=2.
设x1,x2是方程ax2+bx+c=0的两根,
则x1+x2=-,x1·x2=.
∵x+x=10,∴(x1+x2)2-2x1x2=10,
即2-=10,∴42-=10,
∴a=1,b=-4.
∴g(x)=x2-4x+3.
解:(1)由题意,得
y=
(2)x∈(0,10],0.15x≤1.5.
又∵y=5.5,∴x>10,
∴1.5+2log5(x-9)=5.5,∴x=34.
∴老江的销售利润是34万元.
解:(1)补全f(x)的图象如图①所示.
①
(2)当x≥0时,设f(x)=a(x-1)2-2,由f(0)=0得,a=2,
所以此时,f(x)=2(x-1)2-2,即f(x)=2x2-4x,
当x<0时,-x>0,
所以f(-x)=2(-x)2-4(-x)=2x2+4x,①
又f(-x)=-f(x),代入①,得f(x)=-2x2-4x,
所以f(x)=
(3)函数y=|f(x)|的图象如图②所示.
②
由图可知,当a<0时,方程无解;
当a=0时,方程有三个解;
当0
当a>2时,方程有2个解.
20、解:(1)由题意知f(x)=
图象如图所示.
(2)当a<-1时,f(x)-a=0无解;
当a=-1时,f(x)-a=0有两个实数根;
当-1
当a>0时,f(x)-a=0有两个实数根.
21、解:(1)∵g(x)为偶函数,∴g(-x)=g(x),
即log4(4-x+1)-mx=log4(4x+1)+mx,
∴log4-log4(4x+1)=2mx,
∴(2m+1)x=0,∴m=-.
(2)依题意知,log4(4x+1)-x=log4(a·2x-a),
整理,得log4(4x+1)=log4 [(a·2x-a)2x],
∴4x+1=(a·2x-a)·2x(*).
令t=2x,则(*)变为(1-a)t2+at+1=0(**)只需其仅有一正根.
①当a=1时,t=-1不合题意;
②当(**)式有一正一负根时,∴得a>1;
③当(**)式有两相等的正根时,Δ=0,∴a=±2-2,且>0,
∴a=-2-2.
综上所述,a的取值范围为{a|a>1或a=-2-2}.
22、解:(1)设f(x)=k1x,g(x)=k2,
所以f(1)==k1,
g(1)==k2,即f(x)=x(x≥0),g(x)=(x≥0).
(2)设投资债券类产品x万元,则股票类投资为(20-x)万元.
依题意,得
y=f(x)+g(20-x)
=+(0≤x≤20).
令t=(0≤t≤2).
则y=+t=-(t-2)2+3,
所以当t=2,即x=16(万元)时,收益最大,最大收益为3万元.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
