人教版八年级数学上册13.1轴对称精选练习(含答案)
文档属性
| 名称 | 人教版八年级数学上册13.1轴对称精选练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 323.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-09 10:08:07 | ||
图片预览


文档简介
13.1 轴对称精选练习(含答案)-人教版八年级上册
一.选择题
1.下列说法正确的是( )
A.同旁内角互补
B.三角分别相等的两个三角形全等
C.如果△ABC满足∠A:∠B:∠C=3:4:5,则△ABC是锐角三角形
D.一个角的对称轴是它的角平分线
2.如图,已知直线l和直线l外一点P,下列说法不正确的是( )
A.过点P有且只有一条直线与直线l平行
B.过点P有且只有一条直线与直线l垂直
C.在连接点P和直线l上各点的线段中,与直线l垂直的线段最短
D.过点P作直线l的垂直平分线,只能作一条
3.如图,∠AOB=30°,点P在∠AOB的内部,点C,D分别是点P关于OA、OB的对称点,连接CD交OA、OB分别于点E,F;若△PEF的周长的为10,则线段OP=( )
A.8 B.9 C.10 D.11
4.△ABC中,BC=10,AB的垂直平分线与AC的垂直平分线分别交BC于点D,E,且DE=4,则AD+AE的值为( )
A.6 B.14 C.6或14 D.8或12
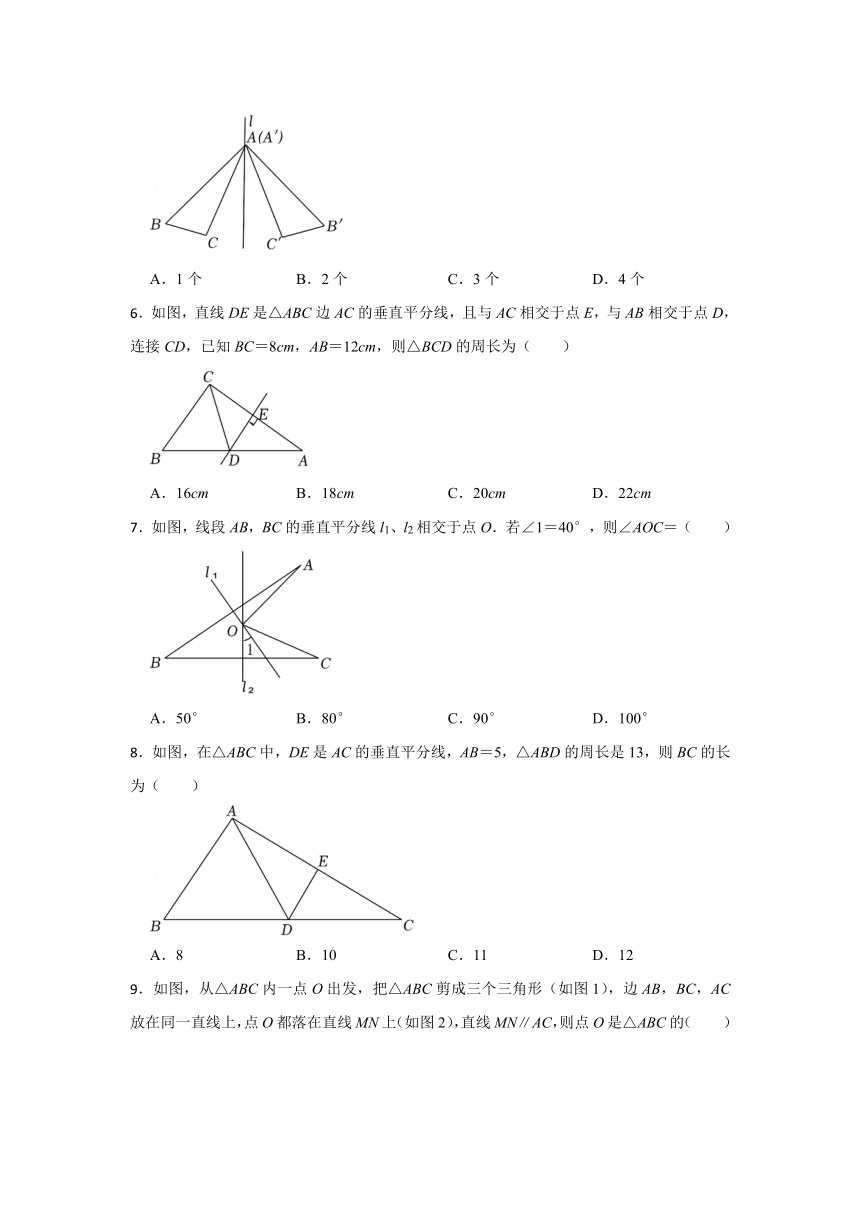
.如图,△ABC和△A'B'C'关于直线l对称,下列结论:(1)△ABC≌△A'B'C';(2)∠BAC=∠B'A'C';(3)直线l垂直平分CC';(4)直线l平分∠CAC'.正确的有( )
A.1个 B.2个 C.3个 D.4个
.如图,直线DE是△ABC边AC的垂直平分线,且与AC相交于点E,与AB相交于点D,连接CD,已知BC=8cm,AB=12cm,则△BCD的周长为( )
A.16cm B.18cm C.20cm D.22cm
.如图,线段AB,BC的垂直平分线l1、l2相交于点O.若∠1=40°,则∠AOC=( )
A.50° B.80° C.90° D.100°
.如图,在△ABC中,DE是AC的垂直平分线,AB=5,△ABD的周长是13,则BC的长为( )
A.8 B.10 C.11 D.12
.如图,从△ABC内一点O出发,把△ABC剪成三个三角形(如图1),边AB,BC,AC放在同一直线上,点O都落在直线MN上(如图2),直线MN∥AC,则点O是△ABC的( )
A.三条角平分线的交点 B.三条高的交点
C.三条中线的交点 D.三边中垂线的交点
.如图,若△ABC与△A'B'C'关于直线MN对称,BB'交MN于点O,则下列说法中,不一定正确的是( )
A.AC=A'C' B.AB∥B'C' C.AA'⊥MN D.BO=B'O
二.填空题
.如图,D,E分别是AB,AC的中点,CD⊥AB,垂足为D,BE⊥AC垂足为E,CD,BE交于点F,DF=2,则BE= .
.如图,在平面直角坐标系中,点A(0,3),B(2,5),M(3,2).在第一象限内找一点横坐标、纵坐标均为整数的点C,使得点M是△ABC的三边垂直平分线的交点,则点C的坐标为 .
.如图,在△ABC中,BC=8,AB的中垂线交BC于点D,AC的中垂线交BC于点E,则△ADE的周长等于 .
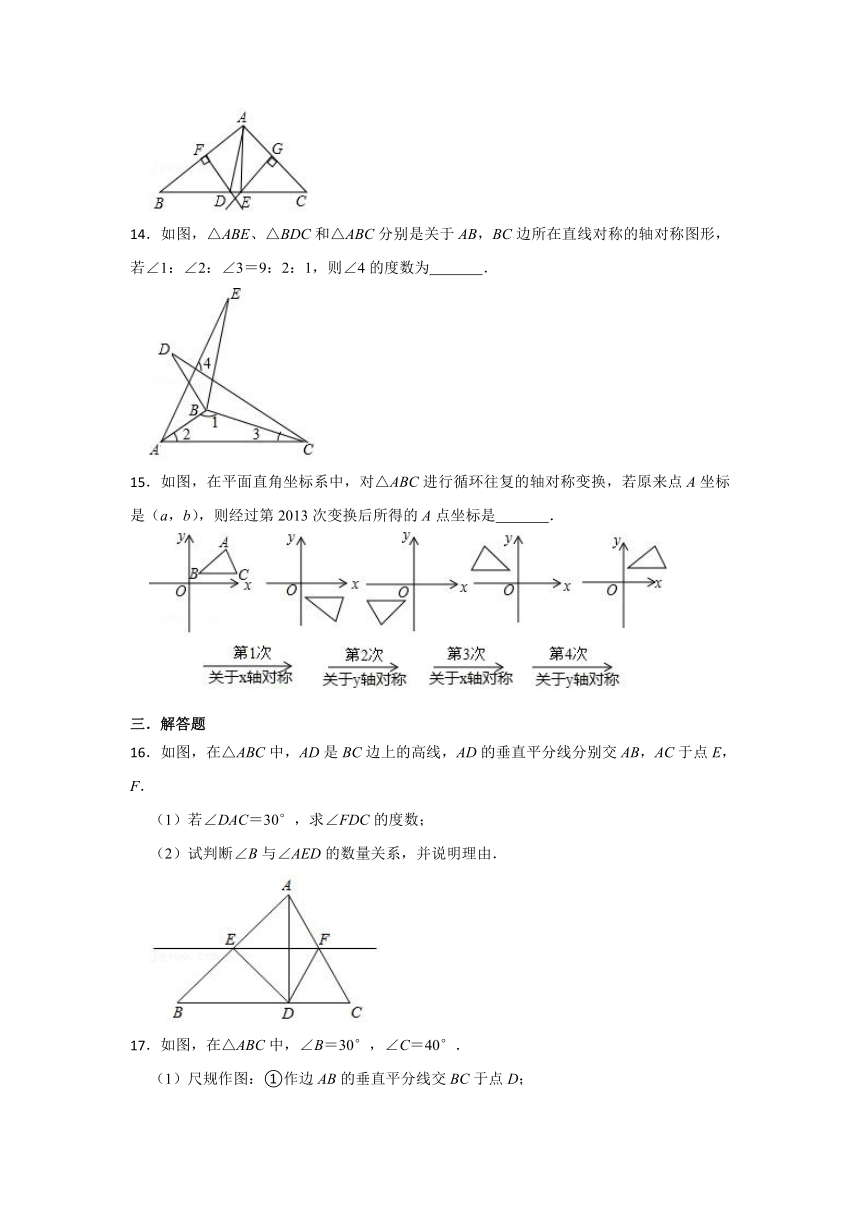
.如图,△ABE、△BDC和△ABC分别是关于AB,BC边所在直线对称的轴对称图形,若∠1:∠2:∠3=9:2:1,则∠4的度数为 .
.如图,在平面直角坐标系中,对△ABC进行循环往复的轴对称变换,若原来点A坐标是(a,b),则经过第2013次变换后所得的A点坐标是 .
解答题
.如图,在△ABC中,AD是BC边上的高线,AD的垂直平分线分别交AB,AC于点E,F.
(1)若∠DAC=30°,求∠FDC的度数;
(2)试判断∠B与∠AED的数量关系,并说明理由.
.如图,在△ABC中,∠B=30°,∠C=40°.
(1)尺规作图:①作边AB的垂直平分线交BC于点D;
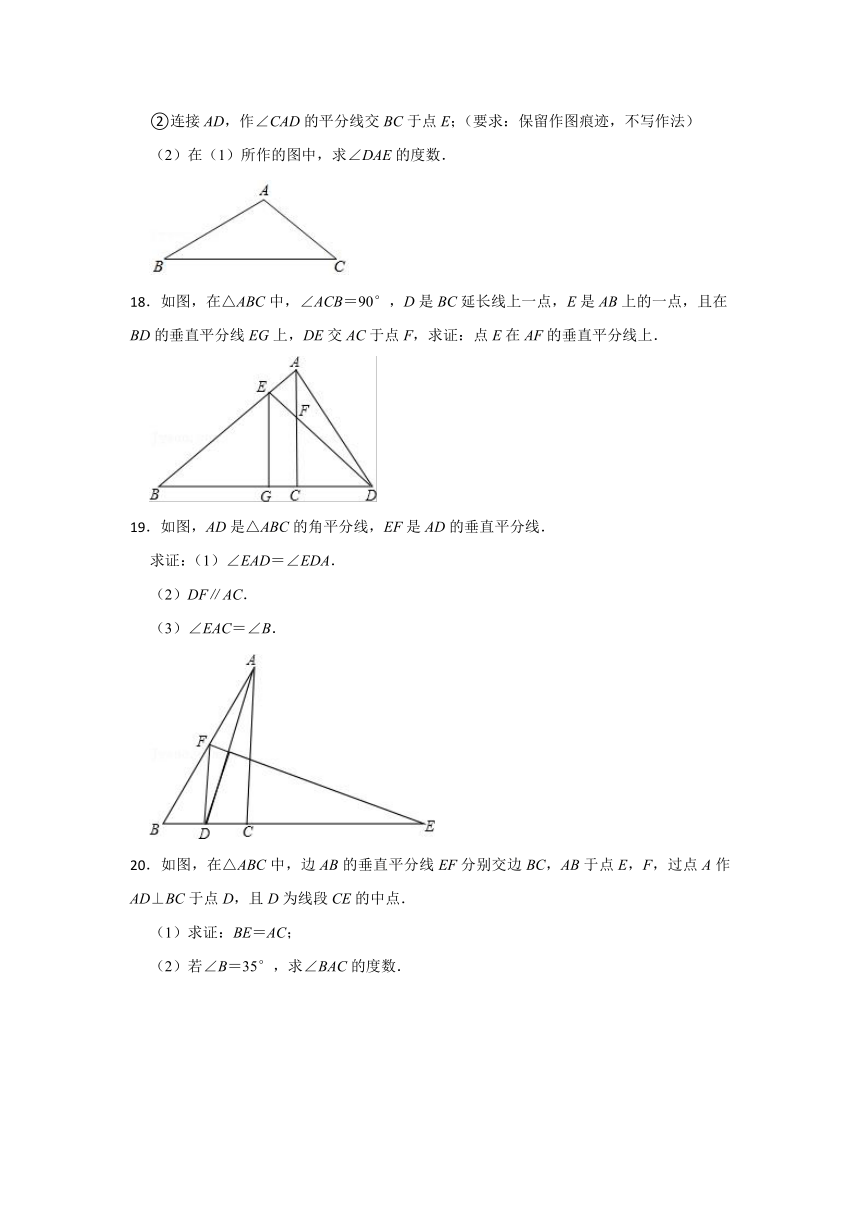
②连接AD,作∠CAD的平分线交BC于点E;(要求:保留作图痕迹,不写作法)
(2)在(1)所作的图中,求∠DAE的度数.
.如图,在△ABC中,∠ACB=90°,D是BC延长线上一点,E是AB上的一点,且在BD的垂直平分线EG上,DE交AC于点F,求证:点E在AF的垂直平分线上.
.如图,AD是△ABC的角平分线,EF是AD的垂直平分线.
求证:(1)∠EAD=∠EDA.
(2)DF∥AC.
(3)∠EAC=∠B.
.如图,在△ABC中,边AB的垂直平分线EF分别交边BC,AB于点E,F,过点A作AD⊥BC于点D,且D为线段CE的中点.
(1)求证:BE=AC;
(2)若∠B=35°,求∠BAC的度数.
参考答案与试题解析
一.选择题
1.【解答】解:A.两直线平行,同旁内角互补,故A选项错误,不符合题意;
B.三边分别相等的两个三角形全等,三角分别相等的两个三角形不一定全等,故B选项错误,不符合题意;
C.如果△ABC满足∠A:∠B:∠C=3:4:5,
那么∠A=×180°=45°,∠B=×180°=60°,∠C=×180°=75°,
则△ABC是锐角三角形,故C选项正确,符合题意;
D.一个角的对称轴是它的角平分线所在的直线,故D选项错误,不符合题意.
故选C.
2.【解答】解:A.过点P有且只有一条直线与直线l平行,故正确,不符合题意;
B.过点P有且只有一条直线与直线l垂直,故正确,不符合题意;
C.在连接点P和直线l上各点的线段中,与直线l垂直的线段最短,故正确,不符合题意;
D.直线没有垂直平分线,故错误,符合题意.
故选:D.
3.【解答】解:连接OD,OC,
∵∠AOB=30°;点D、C分别是点P关于直线OA、OB的对称点,
∴∠DOC=60°,DO=OP=OC,PF=DF,PE=CE,
∴△DOC是等边三角形,
∵△PEF的周长的为10,
∴OP=10.
故选:C.
4.【解答】解:∵AB的垂直平分线与AC的垂直平分线分别交BC于点D,E,
∴AD=BD,AE=EC,
分两种情况:
当BD与CE无重合时,
∵BC=10,DE=4,
∴AD+AE=BD+CE=BC﹣DE=10﹣4=6,
当BD与CE有重合时,
∵BC=10,DE=4,
∴AD+AE=BD+CE=BC+DE=10+4=14,
综上所述:AD+AE的值为:6或14,
故选:C.
.【解答】解:∵△ABC和△AB′C′关于直线l对称,
∴(1)△ABC≌△A'B'C';
(2)∠BAC=∠B'A'C';
(3)直线l垂直平分CC';
(4)直线l平分∠CAC'.
综上所述,正确的结论有4个,
故选:D.
.【解答】解:∵直线DE是AC的垂直平分线,
∴AD=CD,
∵BC=8cm,AB=12cm,
∴△BCD的周长=BC+CD+BD
=BC+AD+BD
=BC+AB
=8+12
=20(cm),
故选:C.
.【解答】解:连接BO,并延长BO到P,
∵线段AB、BC的垂直平分线l1、l2相交于点O,
∴AO=OB=OC,∠BDO=∠BEO=90°,
∴∠DOE+∠ABC=180°,
∵∠DOE+∠1=180°,
∴∠ABC=∠1=40°,
∵OA=OB=OC,
∴∠A=∠ABO,∠OBC=∠C,
∵∠AOP=∠A+∠ABO,∠COP=∠C+∠OBC,
∴∠AOC=∠AOP+∠COP=∠A+∠ABC+∠C=2×40°=80°;
故选:B.
.【解答】解:∵DE是AC的垂直平分线,
∴AD=CD,
∵△ABD的周长是13,
∴AB+AD+BD=13,
∴AB+CD+BD=13,
∴AB+BC=13,
∵AB=5,
∴BC=8,
故选:A.
.【解答】解:如图1,过点O作OD⊥BC于D,OE⊥AC于E,OF⊥AB于F.
∵MN∥AB,
∴OD=OE=OF(夹在平行线间的距离处处相等).
如图2:过点O作OD'⊥BC于D',作OE'⊥AC于E',作OF'⊥AB于F'.
由题意可知:OD=OD',OE=OE',OF=OF',
∴OD'=OE'=OF',
∴图2中的点O是三角形三个内角的平分线的交点,
故选:A.
.【解答】解:∵△ABC与△A'B'C'关于直线MN对称,
∴AC=A′C′,AA′⊥MN,BO=OB′,
故选项A,C,D正确,
故选:B.
二.填空题
.【解答】证明:连接BC,
∵点D是AB中点且CD⊥AB于点D,
∴CD是线段AB的垂直平分线,
∴CA=CB,
同理BA=BC,
∴AC=AB.
∴△ABC是等边三角形,
∴∠A=60°,BE=CD,
在Rt△ABE中,∠ABE=90°﹣∠A=30°,
在Rt△BFD中,BF=2DF,
∵在Rt△ADC中,∠ACD=90°﹣∠A=30°,
又∵∠ABC=∠ACB=60°,
∴∠FBC=∠FCB,
∴CF=BF=2DF=4,
∴BE=CD=6,
故答案为:6.
.【解答】解:∵点M是△ABC三边垂直平分线的交点,
∴MA=MB=MC,
设C(x,y)(x、y为正整数),
∴(x﹣3)2+(y﹣2)2=32+(2﹣3)2=10,
当x=4时,y=5;当x=6时,y=1;当x=6时,y=3,
∴C点坐标为(4,5)或(6,1)或(6,3),
故答案为:(4,5)或(6,1)或(6,3).
.【解答】解:∵AB的中垂线交BC于D,AC的中垂线交BC于E,
∴DA=DB,EA=EC,
则△ADE的周长=AD+DE+AE=BD+DE+EC=BC=8,
故答案为8.
.【解答】解:延长AB交DC于点F,
∵∠1:∠2:∠3=9:2:1,
∴设∠1=9x,∠2=2x,∠3=x,
由∠1+∠2+∠3=180°得:
9x+2x+x=180°,
解得x=15,
故∠1=9×15=135°,∠2=2×15=30°,∠3=1×15=15°,
∴∠DCB=∠E=∠3=15°,∠2=∠EAB=∠D=30°,
∴∠EAC=60°,∠DCA=30°,
∴∠4=∠EAC+∠DCA=90°,
故答案为:90°.
.【解答】解:点A第一次关于x轴对称后在第四象限,
点A第二次关于y轴对称后在第三象限,
点A第三次关于x轴对称后在第二象限,
点A第四次关于y轴对称后在第一象限,即点A回到原始位置,
所以,每四次对称为一个循环组依次循环,
∵2013÷4=503余1,
∴经过第2013次变换后所得的A点与第一次变换的位置相同,在第四象限,坐标为(a,﹣b).
故答案为:(a,﹣b).
三.解答题
.【解答】解:(1)∵AD⊥BC,
∴∠ADC=∠ADB=90°,
∵EF垂直平分AD,
∴AF=DF,
∴∠ADF=∠DAF=30°,
∴∠FDC=90°﹣30°=60°;
(2)∠AED=2∠B,
理由:∵AD⊥BC,EF⊥AD,
∴EF∥BC,
∴∠AEF=∠B,
∵EF垂直平分AD,
∴AE=DE,
∴∠AEF=∠DEF,
∴∠B=∠AEF=∠DEF,
∴∠AED=2∠B.
.【解答】解:(1)如图,点D,射线AE即为所求.
(2)∵DF垂直平分线段AB,
∴DB=DA,
∴∠DAB=∠B=30°,
∵∠C=40°,
∴∠BAC=180°﹣30°﹣40°=110°,
∴∠CAD=110°﹣30°=80°,
∵AE平分∠DAC,
∴∠DAE=∠DAC=40°.
.【解答】解:∵EG垂直平分BD,
∴BE=DE,
∴∠BEG=∠DEG,
∵∠ACB=90°,
∴EG∥AC,
∴∠BEG=∠BAC,∠DEG=∠AFE,
∴∠EAF=∠AFE,
∴AE=EF,
∴点E在AF的垂直平分线上.
.【解答】证明:(1)∵EF是AD的垂直平分线,
∴AE=DE,
∴∠EAD=∠EDA;
(2)∵EF是AD的垂直平分线,
∴AF=DF,
∴∠BAD=∠ADF,
∵AD是△ABC的角平分线,
∴∠BAD=∠CAD,
∴∠ADF=∠CAD,
∴DF∥AC;
(3)由(1)∠EAD=∠EDA,
即∠ADE=∠CAD+∠EAC,
∵∠ADE=∠BAD+∠B,
∠BAD=∠CAD,
∴∠EAC=∠B.
.【解答】(1)证明:连接AE,
∵AD⊥BC于点D,且D为线段CE的中点,
∴AD垂直平分CE,
∴AC=AE,
∵EF垂直平分AB,
∴AE=BE,
∴BE=AC;
(2)解:∵AE=BE,∠B=35°,
∴∠BAE=∠B=35°,
∵AD⊥BC,
∴∠ADB=90°,
∴∠BAD=90°﹣35°=55°,
∴∠EAD=55°﹣35°=20°,
∵AC=AE,
∴∠AED=∠C,
∵∠AED+∠EAD=∠C+∠CAD=90°,
∴∠CAD=∠EAD=20°,
∴∠BAC=∠BAD+∠CAD=55°+20°=75°.
一.选择题
1.下列说法正确的是( )
A.同旁内角互补
B.三角分别相等的两个三角形全等
C.如果△ABC满足∠A:∠B:∠C=3:4:5,则△ABC是锐角三角形
D.一个角的对称轴是它的角平分线
2.如图,已知直线l和直线l外一点P,下列说法不正确的是( )
A.过点P有且只有一条直线与直线l平行
B.过点P有且只有一条直线与直线l垂直
C.在连接点P和直线l上各点的线段中,与直线l垂直的线段最短
D.过点P作直线l的垂直平分线,只能作一条
3.如图,∠AOB=30°,点P在∠AOB的内部,点C,D分别是点P关于OA、OB的对称点,连接CD交OA、OB分别于点E,F;若△PEF的周长的为10,则线段OP=( )
A.8 B.9 C.10 D.11
4.△ABC中,BC=10,AB的垂直平分线与AC的垂直平分线分别交BC于点D,E,且DE=4,则AD+AE的值为( )
A.6 B.14 C.6或14 D.8或12
.如图,△ABC和△A'B'C'关于直线l对称,下列结论:(1)△ABC≌△A'B'C';(2)∠BAC=∠B'A'C';(3)直线l垂直平分CC';(4)直线l平分∠CAC'.正确的有( )
A.1个 B.2个 C.3个 D.4个
.如图,直线DE是△ABC边AC的垂直平分线,且与AC相交于点E,与AB相交于点D,连接CD,已知BC=8cm,AB=12cm,则△BCD的周长为( )
A.16cm B.18cm C.20cm D.22cm
.如图,线段AB,BC的垂直平分线l1、l2相交于点O.若∠1=40°,则∠AOC=( )
A.50° B.80° C.90° D.100°
.如图,在△ABC中,DE是AC的垂直平分线,AB=5,△ABD的周长是13,则BC的长为( )
A.8 B.10 C.11 D.12
.如图,从△ABC内一点O出发,把△ABC剪成三个三角形(如图1),边AB,BC,AC放在同一直线上,点O都落在直线MN上(如图2),直线MN∥AC,则点O是△ABC的( )
A.三条角平分线的交点 B.三条高的交点
C.三条中线的交点 D.三边中垂线的交点
.如图,若△ABC与△A'B'C'关于直线MN对称,BB'交MN于点O,则下列说法中,不一定正确的是( )
A.AC=A'C' B.AB∥B'C' C.AA'⊥MN D.BO=B'O
二.填空题
.如图,D,E分别是AB,AC的中点,CD⊥AB,垂足为D,BE⊥AC垂足为E,CD,BE交于点F,DF=2,则BE= .
.如图,在平面直角坐标系中,点A(0,3),B(2,5),M(3,2).在第一象限内找一点横坐标、纵坐标均为整数的点C,使得点M是△ABC的三边垂直平分线的交点,则点C的坐标为 .
.如图,在△ABC中,BC=8,AB的中垂线交BC于点D,AC的中垂线交BC于点E,则△ADE的周长等于 .
.如图,△ABE、△BDC和△ABC分别是关于AB,BC边所在直线对称的轴对称图形,若∠1:∠2:∠3=9:2:1,则∠4的度数为 .
.如图,在平面直角坐标系中,对△ABC进行循环往复的轴对称变换,若原来点A坐标是(a,b),则经过第2013次变换后所得的A点坐标是 .
解答题
.如图,在△ABC中,AD是BC边上的高线,AD的垂直平分线分别交AB,AC于点E,F.
(1)若∠DAC=30°,求∠FDC的度数;
(2)试判断∠B与∠AED的数量关系,并说明理由.
.如图,在△ABC中,∠B=30°,∠C=40°.
(1)尺规作图:①作边AB的垂直平分线交BC于点D;
②连接AD,作∠CAD的平分线交BC于点E;(要求:保留作图痕迹,不写作法)
(2)在(1)所作的图中,求∠DAE的度数.
.如图,在△ABC中,∠ACB=90°,D是BC延长线上一点,E是AB上的一点,且在BD的垂直平分线EG上,DE交AC于点F,求证:点E在AF的垂直平分线上.
.如图,AD是△ABC的角平分线,EF是AD的垂直平分线.
求证:(1)∠EAD=∠EDA.
(2)DF∥AC.
(3)∠EAC=∠B.
.如图,在△ABC中,边AB的垂直平分线EF分别交边BC,AB于点E,F,过点A作AD⊥BC于点D,且D为线段CE的中点.
(1)求证:BE=AC;
(2)若∠B=35°,求∠BAC的度数.
参考答案与试题解析
一.选择题
1.【解答】解:A.两直线平行,同旁内角互补,故A选项错误,不符合题意;
B.三边分别相等的两个三角形全等,三角分别相等的两个三角形不一定全等,故B选项错误,不符合题意;
C.如果△ABC满足∠A:∠B:∠C=3:4:5,
那么∠A=×180°=45°,∠B=×180°=60°,∠C=×180°=75°,
则△ABC是锐角三角形,故C选项正确,符合题意;
D.一个角的对称轴是它的角平分线所在的直线,故D选项错误,不符合题意.
故选C.
2.【解答】解:A.过点P有且只有一条直线与直线l平行,故正确,不符合题意;
B.过点P有且只有一条直线与直线l垂直,故正确,不符合题意;
C.在连接点P和直线l上各点的线段中,与直线l垂直的线段最短,故正确,不符合题意;
D.直线没有垂直平分线,故错误,符合题意.
故选:D.
3.【解答】解:连接OD,OC,
∵∠AOB=30°;点D、C分别是点P关于直线OA、OB的对称点,
∴∠DOC=60°,DO=OP=OC,PF=DF,PE=CE,
∴△DOC是等边三角形,
∵△PEF的周长的为10,
∴OP=10.
故选:C.
4.【解答】解:∵AB的垂直平分线与AC的垂直平分线分别交BC于点D,E,
∴AD=BD,AE=EC,
分两种情况:
当BD与CE无重合时,
∵BC=10,DE=4,
∴AD+AE=BD+CE=BC﹣DE=10﹣4=6,
当BD与CE有重合时,
∵BC=10,DE=4,
∴AD+AE=BD+CE=BC+DE=10+4=14,
综上所述:AD+AE的值为:6或14,
故选:C.
.【解答】解:∵△ABC和△AB′C′关于直线l对称,
∴(1)△ABC≌△A'B'C';
(2)∠BAC=∠B'A'C';
(3)直线l垂直平分CC';
(4)直线l平分∠CAC'.
综上所述,正确的结论有4个,
故选:D.
.【解答】解:∵直线DE是AC的垂直平分线,
∴AD=CD,
∵BC=8cm,AB=12cm,
∴△BCD的周长=BC+CD+BD
=BC+AD+BD
=BC+AB
=8+12
=20(cm),
故选:C.
.【解答】解:连接BO,并延长BO到P,
∵线段AB、BC的垂直平分线l1、l2相交于点O,
∴AO=OB=OC,∠BDO=∠BEO=90°,
∴∠DOE+∠ABC=180°,
∵∠DOE+∠1=180°,
∴∠ABC=∠1=40°,
∵OA=OB=OC,
∴∠A=∠ABO,∠OBC=∠C,
∵∠AOP=∠A+∠ABO,∠COP=∠C+∠OBC,
∴∠AOC=∠AOP+∠COP=∠A+∠ABC+∠C=2×40°=80°;
故选:B.
.【解答】解:∵DE是AC的垂直平分线,
∴AD=CD,
∵△ABD的周长是13,
∴AB+AD+BD=13,
∴AB+CD+BD=13,
∴AB+BC=13,
∵AB=5,
∴BC=8,
故选:A.
.【解答】解:如图1,过点O作OD⊥BC于D,OE⊥AC于E,OF⊥AB于F.
∵MN∥AB,
∴OD=OE=OF(夹在平行线间的距离处处相等).
如图2:过点O作OD'⊥BC于D',作OE'⊥AC于E',作OF'⊥AB于F'.
由题意可知:OD=OD',OE=OE',OF=OF',
∴OD'=OE'=OF',
∴图2中的点O是三角形三个内角的平分线的交点,
故选:A.
.【解答】解:∵△ABC与△A'B'C'关于直线MN对称,
∴AC=A′C′,AA′⊥MN,BO=OB′,
故选项A,C,D正确,
故选:B.
二.填空题
.【解答】证明:连接BC,
∵点D是AB中点且CD⊥AB于点D,
∴CD是线段AB的垂直平分线,
∴CA=CB,
同理BA=BC,
∴AC=AB.
∴△ABC是等边三角形,
∴∠A=60°,BE=CD,
在Rt△ABE中,∠ABE=90°﹣∠A=30°,
在Rt△BFD中,BF=2DF,
∵在Rt△ADC中,∠ACD=90°﹣∠A=30°,
又∵∠ABC=∠ACB=60°,
∴∠FBC=∠FCB,
∴CF=BF=2DF=4,
∴BE=CD=6,
故答案为:6.
.【解答】解:∵点M是△ABC三边垂直平分线的交点,
∴MA=MB=MC,
设C(x,y)(x、y为正整数),
∴(x﹣3)2+(y﹣2)2=32+(2﹣3)2=10,
当x=4时,y=5;当x=6时,y=1;当x=6时,y=3,
∴C点坐标为(4,5)或(6,1)或(6,3),
故答案为:(4,5)或(6,1)或(6,3).
.【解答】解:∵AB的中垂线交BC于D,AC的中垂线交BC于E,
∴DA=DB,EA=EC,
则△ADE的周长=AD+DE+AE=BD+DE+EC=BC=8,
故答案为8.
.【解答】解:延长AB交DC于点F,
∵∠1:∠2:∠3=9:2:1,
∴设∠1=9x,∠2=2x,∠3=x,
由∠1+∠2+∠3=180°得:
9x+2x+x=180°,
解得x=15,
故∠1=9×15=135°,∠2=2×15=30°,∠3=1×15=15°,
∴∠DCB=∠E=∠3=15°,∠2=∠EAB=∠D=30°,
∴∠EAC=60°,∠DCA=30°,
∴∠4=∠EAC+∠DCA=90°,
故答案为:90°.
.【解答】解:点A第一次关于x轴对称后在第四象限,
点A第二次关于y轴对称后在第三象限,
点A第三次关于x轴对称后在第二象限,
点A第四次关于y轴对称后在第一象限,即点A回到原始位置,
所以,每四次对称为一个循环组依次循环,
∵2013÷4=503余1,
∴经过第2013次变换后所得的A点与第一次变换的位置相同,在第四象限,坐标为(a,﹣b).
故答案为:(a,﹣b).
三.解答题
.【解答】解:(1)∵AD⊥BC,
∴∠ADC=∠ADB=90°,
∵EF垂直平分AD,
∴AF=DF,
∴∠ADF=∠DAF=30°,
∴∠FDC=90°﹣30°=60°;
(2)∠AED=2∠B,
理由:∵AD⊥BC,EF⊥AD,
∴EF∥BC,
∴∠AEF=∠B,
∵EF垂直平分AD,
∴AE=DE,
∴∠AEF=∠DEF,
∴∠B=∠AEF=∠DEF,
∴∠AED=2∠B.
.【解答】解:(1)如图,点D,射线AE即为所求.
(2)∵DF垂直平分线段AB,
∴DB=DA,
∴∠DAB=∠B=30°,
∵∠C=40°,
∴∠BAC=180°﹣30°﹣40°=110°,
∴∠CAD=110°﹣30°=80°,
∵AE平分∠DAC,
∴∠DAE=∠DAC=40°.
.【解答】解:∵EG垂直平分BD,
∴BE=DE,
∴∠BEG=∠DEG,
∵∠ACB=90°,
∴EG∥AC,
∴∠BEG=∠BAC,∠DEG=∠AFE,
∴∠EAF=∠AFE,
∴AE=EF,
∴点E在AF的垂直平分线上.
.【解答】证明:(1)∵EF是AD的垂直平分线,
∴AE=DE,
∴∠EAD=∠EDA;
(2)∵EF是AD的垂直平分线,
∴AF=DF,
∴∠BAD=∠ADF,
∵AD是△ABC的角平分线,
∴∠BAD=∠CAD,
∴∠ADF=∠CAD,
∴DF∥AC;
(3)由(1)∠EAD=∠EDA,
即∠ADE=∠CAD+∠EAC,
∵∠ADE=∠BAD+∠B,
∠BAD=∠CAD,
∴∠EAC=∠B.
.【解答】(1)证明:连接AE,
∵AD⊥BC于点D,且D为线段CE的中点,
∴AD垂直平分CE,
∴AC=AE,
∵EF垂直平分AB,
∴AE=BE,
∴BE=AC;
(2)解:∵AE=BE,∠B=35°,
∴∠BAE=∠B=35°,
∵AD⊥BC,
∴∠ADB=90°,
∴∠BAD=90°﹣35°=55°,
∴∠EAD=55°﹣35°=20°,
∵AC=AE,
∴∠AED=∠C,
∵∠AED+∠EAD=∠C+∠CAD=90°,
∴∠CAD=∠EAD=20°,
∴∠BAC=∠BAD+∠CAD=55°+20°=75°.
