人教版八年级数学下册19.1函数同步练习(含答案)
文档属性
| 名称 | 人教版八年级数学下册19.1函数同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 624.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-09 10:09:54 | ||
图片预览


文档简介
人教版八下 19.1 函数
一、选择题(共12小题)
1. 在正方形面积公式 中,变量为
A. 和 B. , 和 C. 和 D. 和
2. 函数 中自变量 的取值范围是
A. B. C. D.
3. 下面的表格中列出意向试验的统计数据,表示将弹力球从高处落下时,弹跳高度 与下落高度 的关系,则能表示这种关系的等式是
A. B. C. D.
4. 与函数 的定义域相同的是
A. B. C. D.
5. 一列从小到大,按某种规律排列的数如下:,,,,,,,,,,,,第 ( 为正整数)个数记作 , 是 的函数,则 的值可能是下列各数中的
A. B. C. D.
6. 如图,在平行四边形 中,直线 .将直线 沿 从 点匀速平移至 点,在运动过程中,直线 与平行四边形 两边的交点分别记为点 ,.设线段 的长为 , 平移时间为 则下列图象中,能表示 与 的函数关系的图象大致是
A. B.
C. D.
7. 在 月份,某地的蔬菜批发市场指导菜农生产和销售某种蔬菜,并向他们提供了这种蔬菜每千克售价与每千克成本的信息如图所示,则出售该种蔬菜每千克利润最大的月份可能是
A. 月份 B. 月份 C. 月份 D. 月份
8. 若函数 ,,则函数 中,自变量 的取值范围是
A. B.
C. 且 D.
9. 已知函数 ,当函数值为 时,则 的值为
A. B. C. D.
10. 在一条笔直的航道上依次有甲,乙,丙三个港口,一艘船从甲出发,沿直线匀速行驶经过乙港驶向丙港,最终达到丙港,设行驶 后,与乙港的距离为 , 与 的函数关系如图所示,则下列说法正确的是
A. 甲港与丙港的距离是 B. 船在中途休息了 小时
C. 船的行驶速度是 D. 从乙港到达丙港共花了 小时
11. 在函数 中,自变量 的值可以是
A. B. C. D.
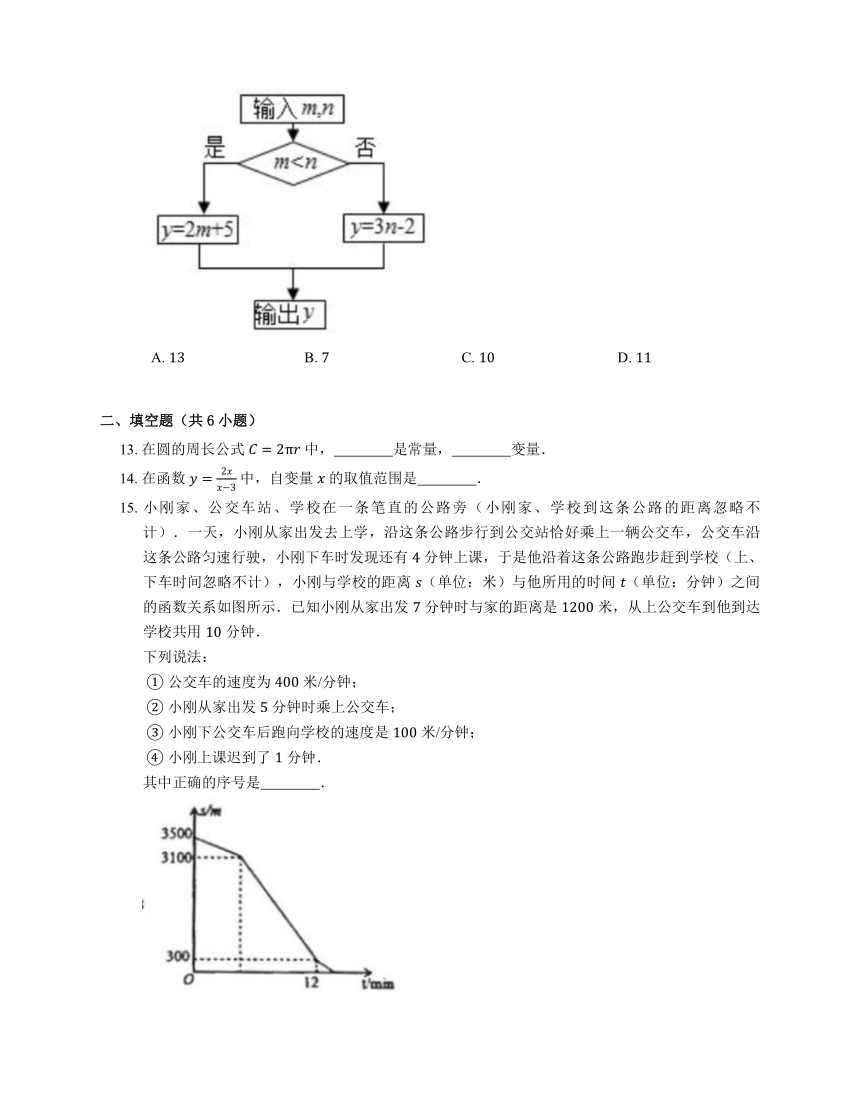
12. 根据如图所示的计算程序计算变量 的值,若输入 , 时,则输出 的值是
A. B. C. D.
二、填空题(共6小题)
13. 在圆的周长公式 中, 是常量, 变量.
14. 在函数 中,自变量 的取值范围是 .
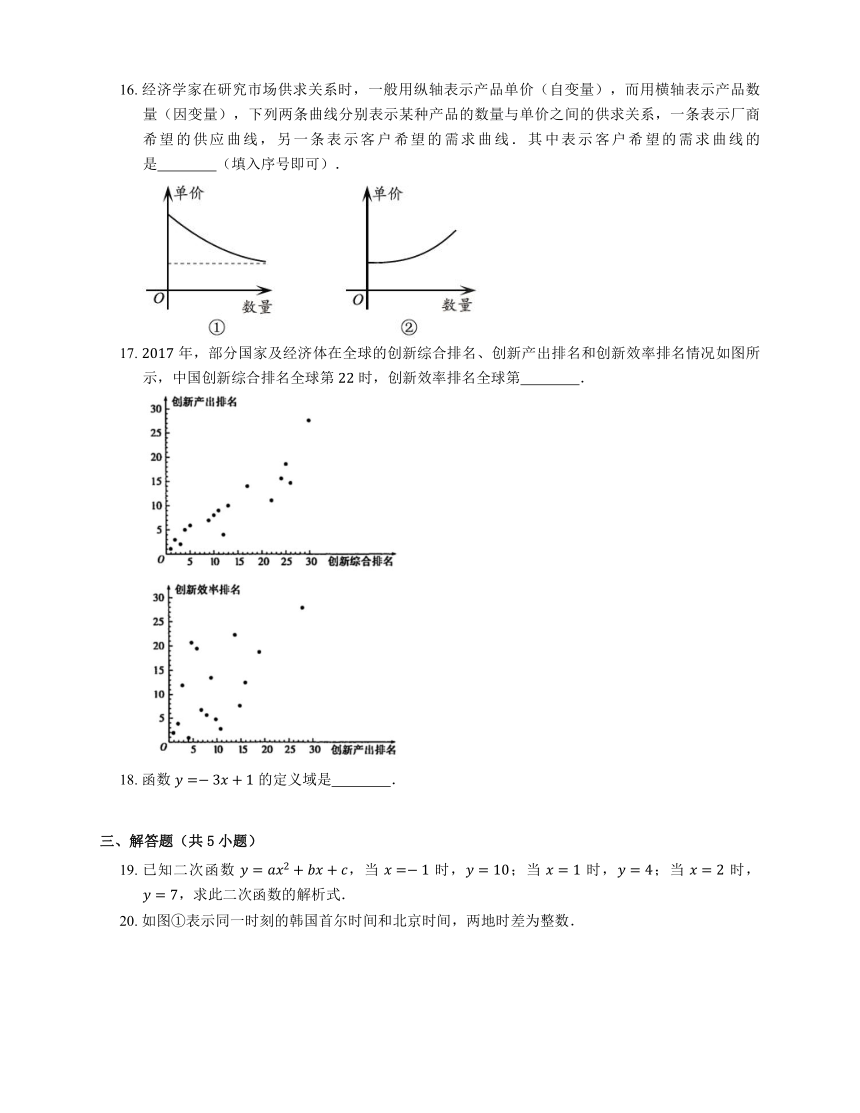
15. 小刚家、公交车站、学校在一条笔直的公路旁(小刚家、学校到这条公路的距离忽略不计).一天,小刚从家出发去上学,沿这条公路步行到公交站恰好乘上一辆公交车,公交车沿这条公路匀速行驶,小刚下车时发现还有 分钟上课,于是他沿着这条公路跑步赶到学校(上、下车时间忽略不计),小刚与学校的距离 (单位:米)与他所用的时间 (单位:分钟)之间的函数关系如图所示.已知小刚从家出发 分钟时与家的距离是 米,从上公交车到他到达学校共用 分钟.
下列说法:
公交车的速度为 米/分钟;
小刚从家出发 分钟时乘上公交车;
小刚下公交车后跑向学校的速度是 米/分钟;
小刚上课迟到了 分钟.
其中正确的序号是 .
16. 经济学家在研究市场供求关系时,一般用纵轴表示产品单价(自变量),而用横轴表示产品数量(因变量),下列两条曲线分别表示某种产品的数量与单价之间的供求关系,一条表示厂商希望的供应曲线,另一条表示客户希望的需求曲线.其中表示客户希望的需求曲线的是 (填入序号即可).
17. 年,部分国家及经济体在全球的创新综合排名、创新产出排名和创新效率排名情况如图所示,中国创新综合排名全球第 时,创新效率排名全球第 .
18. 函数 的定义域是 .
三、解答题(共5小题)
19. 已知二次函数 ,当 时,;当 时,;当 时,,求此二次函数的解析式.
20. 如图①表示同一时刻的韩国首尔时间和北京时间,两地时差为整数.
(1)设北京时间为 (时),首尔时间为 (时),若 ,求 关于 的函数表达式,并填写下表(同一时刻的两地时间).
(2)如图②表示同一时刻的英国伦敦(夏时制)时间和北京时间,两地时差为整数.如果现在伦敦(夏时制)时间为 ,那么此时韩国首尔时间是多少
21. 如果设 ,那么 表示当 时, 的值,即 .
如:.
(1)求 的值;
(2)求 的值;
(3)计算:(结果用含有 的代数式表示, 为正整数).
22. 某商店出售一种商品,质量 与售价 之间的关系如下表:
(1)写出售价 (元)与质量 (千克)的函数关系式;
(2)小张想买此种商品 千克,应付款多少元
23. 如图,在靠墙(墙长为 )的地方围建一个长方形的养鸡场,一边靠墙,另外三边用竹篱笆围成,如果竹篱笆总长为 .
(1)求养鸡场的长 与宽 之间的函数表达式();
(2)求自变量 的取值范围.
答案
1. C
2. B
【解析】由题意,得 ,解得 .
3. B
【解析】每组的 值都是 值的一半.
4. A
5. C
【解析】这列数字的规律是后一个是前面相邻数字加 ,
,
若 ,则 ,,与 为正整数矛盾,排除A;
若 ,则 ,,与 为正整数矛盾,排除B;
若 ,则 ,,符合题意.
若 ,则 ,与 为正整数矛盾,D错误.
6. D 【解析】①当点 在 上运动时,
设直线 交直线 于点 ,,,
则 ,,
则 ,
,为一次函数;
②当直线 在 之间运动时,
为常数;
③当直线 在 上运动时,
同理可得: 的表达式为一次函数,
故选:D.
7. C
8. C
9. B
10. D
11. C
12. B
【解析】,,
,
,
当 时,.
13. , 与
14.
【解析】由题意可知:,
解得 .
15.
【解析】 小刚从家出发 分钟时与家的距离是 米,
即小刚从家出发 分钟时距离学校 ,
公交车的速度为: 米/分钟,
故①正确;
由①知公交车速度为 米/分钟,
公交车行驶的时间为 分钟,
小刚从家出发乘上公交车是在第 分钟时,
故②正确;
从上公交车到他到达学校共用 分钟,
小刚下公交车后跑向学校的速度是 米/分钟,
故③正确;
小刚从小车至到达学校所用时间为 分钟,
而小刚下车时发现还有 分钟上课,
小刚下车较上课提前 分钟,
故④错误.
故答案为:①②③.
16. ①
17.
【解析】由中国创新综合排名为全球第 ,可以发现创新产出排名为全球第 ,当创新产出排名为全球第 时,创新效率排名为全球第 .
18. 一切实数
19. .
20. (1) 从题图①看出,同一时刻,首尔时间比北京时间多 小时,
所以 关于 的函数表达式是 ,.
填表如下:
(2) 设伦敦(夏时制)时间为 时,则北京时间为 时,
结合()可得,韩国首尔时间为 时,
所以当伦敦(夏时制)时间为 ,韩国首尔时间为 .
21. (1) 当 时,.
当 时,,
.
(2) .
(3) .
22. (1) .
(2) 当 时,由()得,
.
答:应付 元.
23. (1) 根据题意,得 ,即 .
(2) 根据题意,有 ,
,
解得 .
又 ,
,
解得 .
自变量 的取值范围是 .
一、选择题(共12小题)
1. 在正方形面积公式 中,变量为
A. 和 B. , 和 C. 和 D. 和
2. 函数 中自变量 的取值范围是
A. B. C. D.
3. 下面的表格中列出意向试验的统计数据,表示将弹力球从高处落下时,弹跳高度 与下落高度 的关系,则能表示这种关系的等式是
A. B. C. D.
4. 与函数 的定义域相同的是
A. B. C. D.
5. 一列从小到大,按某种规律排列的数如下:,,,,,,,,,,,,第 ( 为正整数)个数记作 , 是 的函数,则 的值可能是下列各数中的
A. B. C. D.
6. 如图,在平行四边形 中,直线 .将直线 沿 从 点匀速平移至 点,在运动过程中,直线 与平行四边形 两边的交点分别记为点 ,.设线段 的长为 , 平移时间为 则下列图象中,能表示 与 的函数关系的图象大致是
A. B.
C. D.
7. 在 月份,某地的蔬菜批发市场指导菜农生产和销售某种蔬菜,并向他们提供了这种蔬菜每千克售价与每千克成本的信息如图所示,则出售该种蔬菜每千克利润最大的月份可能是
A. 月份 B. 月份 C. 月份 D. 月份
8. 若函数 ,,则函数 中,自变量 的取值范围是
A. B.
C. 且 D.
9. 已知函数 ,当函数值为 时,则 的值为
A. B. C. D.
10. 在一条笔直的航道上依次有甲,乙,丙三个港口,一艘船从甲出发,沿直线匀速行驶经过乙港驶向丙港,最终达到丙港,设行驶 后,与乙港的距离为 , 与 的函数关系如图所示,则下列说法正确的是
A. 甲港与丙港的距离是 B. 船在中途休息了 小时
C. 船的行驶速度是 D. 从乙港到达丙港共花了 小时
11. 在函数 中,自变量 的值可以是
A. B. C. D.
12. 根据如图所示的计算程序计算变量 的值,若输入 , 时,则输出 的值是
A. B. C. D.
二、填空题(共6小题)
13. 在圆的周长公式 中, 是常量, 变量.
14. 在函数 中,自变量 的取值范围是 .
15. 小刚家、公交车站、学校在一条笔直的公路旁(小刚家、学校到这条公路的距离忽略不计).一天,小刚从家出发去上学,沿这条公路步行到公交站恰好乘上一辆公交车,公交车沿这条公路匀速行驶,小刚下车时发现还有 分钟上课,于是他沿着这条公路跑步赶到学校(上、下车时间忽略不计),小刚与学校的距离 (单位:米)与他所用的时间 (单位:分钟)之间的函数关系如图所示.已知小刚从家出发 分钟时与家的距离是 米,从上公交车到他到达学校共用 分钟.
下列说法:
公交车的速度为 米/分钟;
小刚从家出发 分钟时乘上公交车;
小刚下公交车后跑向学校的速度是 米/分钟;
小刚上课迟到了 分钟.
其中正确的序号是 .
16. 经济学家在研究市场供求关系时,一般用纵轴表示产品单价(自变量),而用横轴表示产品数量(因变量),下列两条曲线分别表示某种产品的数量与单价之间的供求关系,一条表示厂商希望的供应曲线,另一条表示客户希望的需求曲线.其中表示客户希望的需求曲线的是 (填入序号即可).
17. 年,部分国家及经济体在全球的创新综合排名、创新产出排名和创新效率排名情况如图所示,中国创新综合排名全球第 时,创新效率排名全球第 .
18. 函数 的定义域是 .
三、解答题(共5小题)
19. 已知二次函数 ,当 时,;当 时,;当 时,,求此二次函数的解析式.
20. 如图①表示同一时刻的韩国首尔时间和北京时间,两地时差为整数.
(1)设北京时间为 (时),首尔时间为 (时),若 ,求 关于 的函数表达式,并填写下表(同一时刻的两地时间).
(2)如图②表示同一时刻的英国伦敦(夏时制)时间和北京时间,两地时差为整数.如果现在伦敦(夏时制)时间为 ,那么此时韩国首尔时间是多少
21. 如果设 ,那么 表示当 时, 的值,即 .
如:.
(1)求 的值;
(2)求 的值;
(3)计算:(结果用含有 的代数式表示, 为正整数).
22. 某商店出售一种商品,质量 与售价 之间的关系如下表:
(1)写出售价 (元)与质量 (千克)的函数关系式;
(2)小张想买此种商品 千克,应付款多少元
23. 如图,在靠墙(墙长为 )的地方围建一个长方形的养鸡场,一边靠墙,另外三边用竹篱笆围成,如果竹篱笆总长为 .
(1)求养鸡场的长 与宽 之间的函数表达式();
(2)求自变量 的取值范围.
答案
1. C
2. B
【解析】由题意,得 ,解得 .
3. B
【解析】每组的 值都是 值的一半.
4. A
5. C
【解析】这列数字的规律是后一个是前面相邻数字加 ,
,
若 ,则 ,,与 为正整数矛盾,排除A;
若 ,则 ,,与 为正整数矛盾,排除B;
若 ,则 ,,符合题意.
若 ,则 ,与 为正整数矛盾,D错误.
6. D 【解析】①当点 在 上运动时,
设直线 交直线 于点 ,,,
则 ,,
则 ,
,为一次函数;
②当直线 在 之间运动时,
为常数;
③当直线 在 上运动时,
同理可得: 的表达式为一次函数,
故选:D.
7. C
8. C
9. B
10. D
11. C
12. B
【解析】,,
,
,
当 时,.
13. , 与
14.
【解析】由题意可知:,
解得 .
15.
【解析】 小刚从家出发 分钟时与家的距离是 米,
即小刚从家出发 分钟时距离学校 ,
公交车的速度为: 米/分钟,
故①正确;
由①知公交车速度为 米/分钟,
公交车行驶的时间为 分钟,
小刚从家出发乘上公交车是在第 分钟时,
故②正确;
从上公交车到他到达学校共用 分钟,
小刚下公交车后跑向学校的速度是 米/分钟,
故③正确;
小刚从小车至到达学校所用时间为 分钟,
而小刚下车时发现还有 分钟上课,
小刚下车较上课提前 分钟,
故④错误.
故答案为:①②③.
16. ①
17.
【解析】由中国创新综合排名为全球第 ,可以发现创新产出排名为全球第 ,当创新产出排名为全球第 时,创新效率排名为全球第 .
18. 一切实数
19. .
20. (1) 从题图①看出,同一时刻,首尔时间比北京时间多 小时,
所以 关于 的函数表达式是 ,.
填表如下:
(2) 设伦敦(夏时制)时间为 时,则北京时间为 时,
结合()可得,韩国首尔时间为 时,
所以当伦敦(夏时制)时间为 ,韩国首尔时间为 .
21. (1) 当 时,.
当 时,,
.
(2) .
(3) .
22. (1) .
(2) 当 时,由()得,
.
答:应付 元.
23. (1) 根据题意,得 ,即 .
(2) 根据题意,有 ,
,
解得 .
又 ,
,
解得 .
自变量 的取值范围是 .
