人教版八年级数学下册18.2特殊的平行四边形(解答题专练)同步练习(含答案)
文档属性
| 名称 | 人教版八年级数学下册18.2特殊的平行四边形(解答题专练)同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 6.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-09 10:13:07 | ||
图片预览


文档简介
人教版八下18.2 特殊的平行四边形(解答题专练)
一、解答题(共30小题)
1. 求证:矩形的对角线相等.
2. 一个矩形的一条对角线长为 ,两条对角线的一个交角为 .求这个矩形的边长(结果保留小数点后两位).
3. 矩形是轴对称图形吗 如果是,它有几条对称轴
4. 八年级(3)班同学要在广场上布置一个矩形的花坛,计划用红花摆成两条对角线.如果一条对角线用了 盆红花,还需要从花房运来多少盆红花 为什么 如果一条对角线用了 盆呢
5. 如图,平行四边形 的对角线 , 相交于点 , 是等边三角形,且 .求平行四边形 的面积.
6. 四边形 是菱形,对角线 , 相交于点 ,且 ,.求 和 的长.
7. 已知菱形的两条对角线的长分别是 和 ,求菱形的周长和面积.
8. 求证:
(1)对角线互相垂直的平行四边形是菱形;
(2)四条边相等的四边形是菱形.
9. 一个平行四边形的一条边长是 ,两条对角线的长分别是 和 ,这是一个特殊的平行四边形吗 为什么 求出它的面积.
10. 如图,两张等宽的纸条交叉叠放在一起,重合部分构成的四边形 是一个菱形吗 为什么
11. (1)把一张长方形纸片按如图方式折一下,就可以裁出正方形纸片.为什么
(2)如何从一块长方形木板中裁出一块最大的正方形木板呢
12. 如图, 是一块正方形场地.小华和小芳在 边上取定了一点 ,测量知,,.这块场地的面积和对角线长分别是多少
13. 满足下列条件的四边形是不是正方形 为什么
()对角线互相垂直且相等的平行四边形;
()对角线互相垂直的矩形;
()对角线相等的菱形;
()对角线互相垂直平分且相等的四边形.
14. 如图,四边形 是平行四边形,对角线 , 相交于点 ,且 .它是一个矩形吗 为什么
15. 求证:四个角都相等的四边形是矩形.
16. 一个木匠要制作矩形的踏板.他在一个对边平行的长木板上分别沿与长边垂直的方向锯了两次,就能得到矩形踏板.为什么
17. 在 中,,.求 , 的度数.
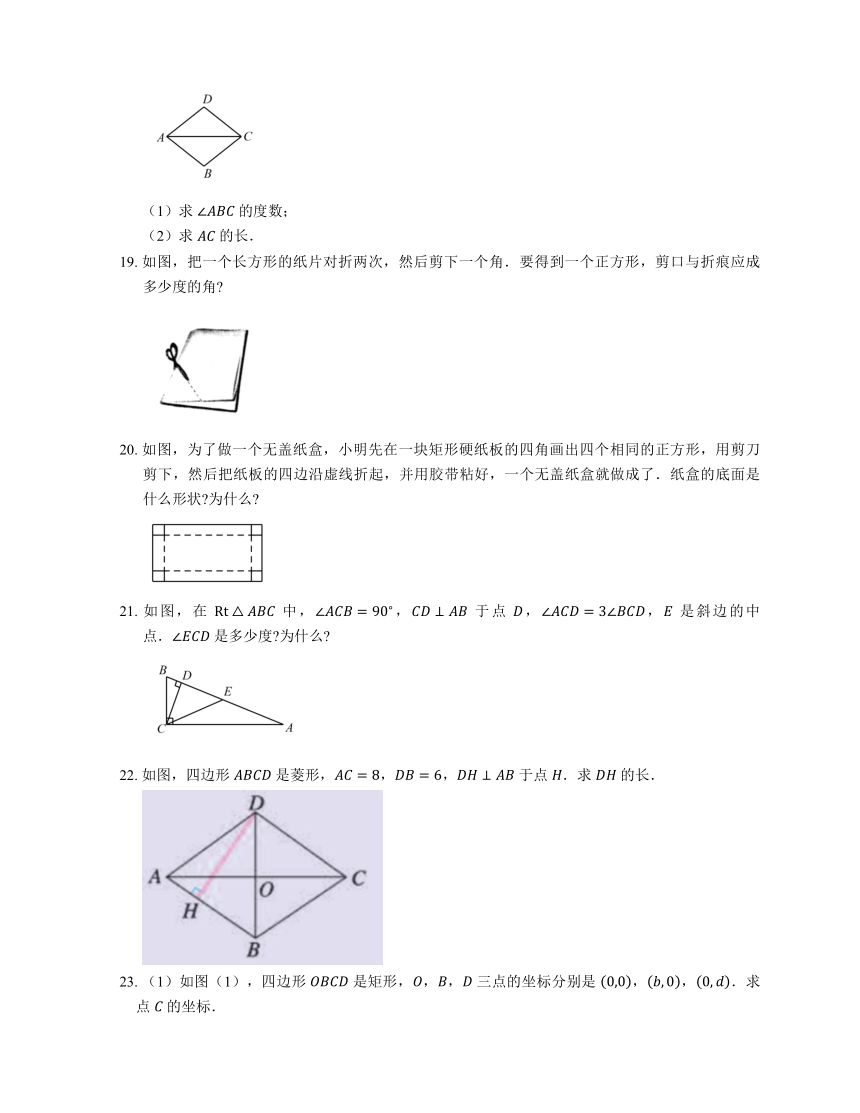
18. 如图,四边形 是菱形,,.
(1)求 的度数;
(2)求 的长.
19. 如图,把一个长方形的纸片对折两次,然后剪下一个角.要得到一个正方形,剪口与折痕应成多少度的角
20. 如图,为了做一个无盖纸盒,小明先在一块矩形硬纸板的四角画出四个相同的正方形,用剪刀剪下,然后把纸板的四边沿虚线折起,并用胶带粘好,一个无盖纸盒就做成了.纸盒的底面是什么形状 为什么
21. 如图,在 中,, 于点 ,, 是斜边的中点. 是多少度 为什么
22. 如图,四边形 是菱形,,, 于点 .求 的长.
23. (1)如图(1),四边形 是矩形,,, 三点的坐标分别是 ,,.求点 的坐标.
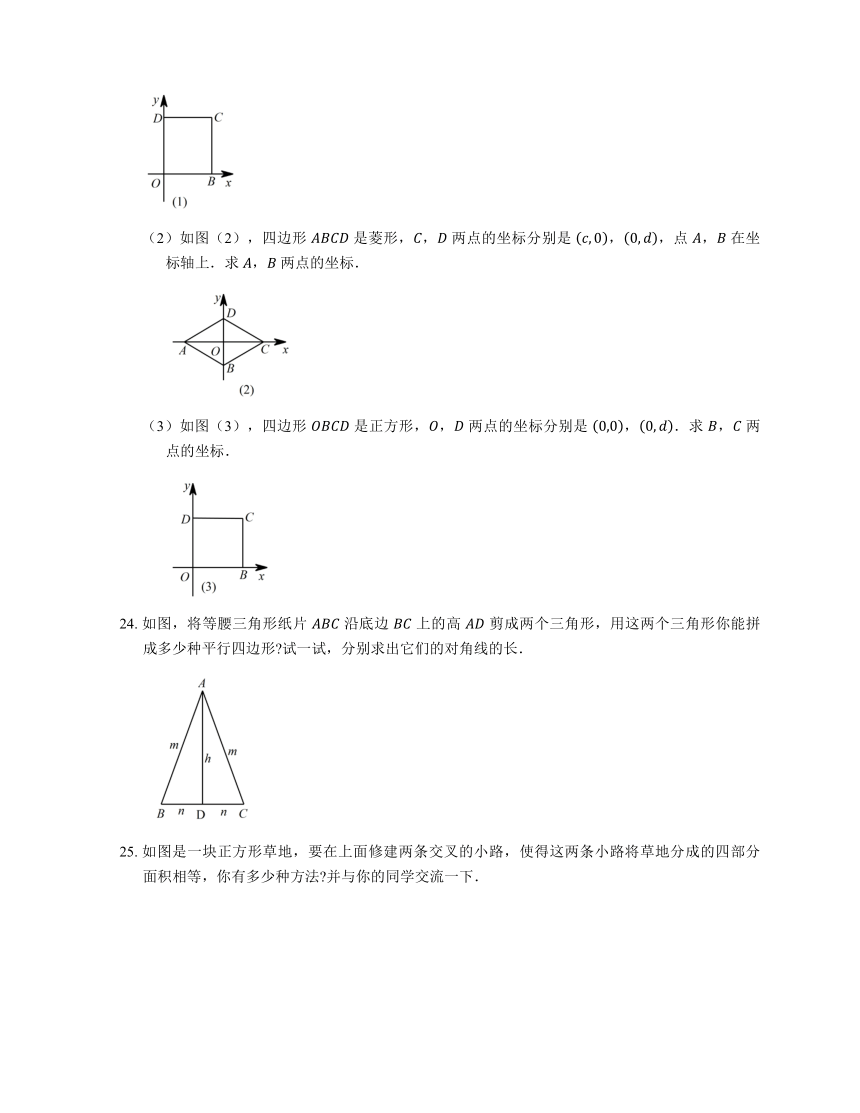
(2)如图(2),四边形 是菱形,, 两点的坐标分别是 ,,点 , 在坐标轴上.求 , 两点的坐标.
(3)如图(3),四边形 是正方形,, 两点的坐标分别是 ,.求 , 两点的坐标.
24. 如图,将等腰三角形纸片 沿底边 上的高 剪成两个三角形,用这两个三角形你能拼成多少种平行四边形 试一试,分别求出它们的对角线的长.
25. 如图是一块正方形草地,要在上面修建两条交叉的小路,使得这两条小路将草地分成的四部分面积相等,你有多少种方法 并与你的同学交流一下.
26. 如图,, 平分 ,且交 于点 , 平分 ,且交 于点 ,连接 .求证:四边形 是菱形.
27. 如图,四边形 是菱形,点 , 分别在 , 上,且 ,,;点 , 分别在 , 上, 与 相交于点 .求证:四边形 , 都是菱形.
28. 如图,,,, 分别是正方形 四条边上的点,且 .试判断四边形 是什么图形,并证明你的结论.
29. 如图,四边形 是正方形. 是 上的任意一点, 于点 ,,且交 于点 .求证:.
30. 如图,在 中,, 分别是边 , 上的中线, 与 相交于点 . 与 的长度有什么关系 边上的中线是否一定过点 为什么 (提示:分别作 , 的中点 ,,连接 ,,,.)
答案
1. 如教科书图 ,证明 .
2. ,.
3. 是.它有两条对称轴,分别是对边中点连线所在的直线.
4. 需要再搬来 盆红花.
根据矩形的对角线相等,以及对角线交点处不放花.
需要再搬来 盆红花.根据矩形的对角线相等,以及对角线交点处要放花.
5. .
6. ,.
7. ,.
8. (1) 略;
(2) 略.
9. 这是一个特殊的平行四边形—— 菱形.由勾股定理的逆定理可知,这个平行四边形的对角线互相垂直.面积为 .
10. 它是一个菱形.
可以证明它的四条边相等.
11. (1) 这样得到的是一组邻边相等,并且一个角是直角的平行四边形,因此它是正方形.
(2) 上面(1)中正方形的面积最大.
12. ,.
13. 个都是.它们都符合正方形的判定条件.
14. 是.利用 ,可知 ,从而 ,平行四边形 的对角线相等,它是一个矩形.
15. 由于四边形的内角和为 ,四个角又都相等,
所以它的四个角都是直角.
因此这个四边形是矩形.
16. 能.这时他得到的是一个角为直角的平行四边形,即矩形.
17. ,.
18. (1) 四边形 是菱形,,
,
.
(2) 连接 交 于点 ,
则 ,,
又 ,
在 中,,
,
.
19.
20. 矩形,它的四个角都是直角.
21. .提示:.
22. .
由 可得.
23. (1) ;
(2) ,;
(3) ,.
24. 种.
可以分别以 ,, 为四边形的一条对角线,得到 种平行四边形,
它们的对角线长分别为 ,(或 );,;,(或 ).
25. 分法有无数种.只要保持两条小路互相垂直,并且都过正方形的中心即可.
26. 由 ,可知 ,同理可得 .从而 ,,四边形 是一组邻边相等的平行四边形,它是菱形.
27. 四边形 , 都是一组邻边相等的平行四边形.
28. 正方形.提示:利用 ,证明四边形 的四条边相等,四个角都是直角.
29. 由 ,可得 ,从而 .
30. , 边上的中线一定过点 .
利用四边形 是平行四边形,可知 ;
设 边上的中线和 相交于点 ,可知 ,从而 与 重合.
一、解答题(共30小题)
1. 求证:矩形的对角线相等.
2. 一个矩形的一条对角线长为 ,两条对角线的一个交角为 .求这个矩形的边长(结果保留小数点后两位).
3. 矩形是轴对称图形吗 如果是,它有几条对称轴
4. 八年级(3)班同学要在广场上布置一个矩形的花坛,计划用红花摆成两条对角线.如果一条对角线用了 盆红花,还需要从花房运来多少盆红花 为什么 如果一条对角线用了 盆呢
5. 如图,平行四边形 的对角线 , 相交于点 , 是等边三角形,且 .求平行四边形 的面积.
6. 四边形 是菱形,对角线 , 相交于点 ,且 ,.求 和 的长.
7. 已知菱形的两条对角线的长分别是 和 ,求菱形的周长和面积.
8. 求证:
(1)对角线互相垂直的平行四边形是菱形;
(2)四条边相等的四边形是菱形.
9. 一个平行四边形的一条边长是 ,两条对角线的长分别是 和 ,这是一个特殊的平行四边形吗 为什么 求出它的面积.
10. 如图,两张等宽的纸条交叉叠放在一起,重合部分构成的四边形 是一个菱形吗 为什么
11. (1)把一张长方形纸片按如图方式折一下,就可以裁出正方形纸片.为什么
(2)如何从一块长方形木板中裁出一块最大的正方形木板呢
12. 如图, 是一块正方形场地.小华和小芳在 边上取定了一点 ,测量知,,.这块场地的面积和对角线长分别是多少
13. 满足下列条件的四边形是不是正方形 为什么
()对角线互相垂直且相等的平行四边形;
()对角线互相垂直的矩形;
()对角线相等的菱形;
()对角线互相垂直平分且相等的四边形.
14. 如图,四边形 是平行四边形,对角线 , 相交于点 ,且 .它是一个矩形吗 为什么
15. 求证:四个角都相等的四边形是矩形.
16. 一个木匠要制作矩形的踏板.他在一个对边平行的长木板上分别沿与长边垂直的方向锯了两次,就能得到矩形踏板.为什么
17. 在 中,,.求 , 的度数.
18. 如图,四边形 是菱形,,.
(1)求 的度数;
(2)求 的长.
19. 如图,把一个长方形的纸片对折两次,然后剪下一个角.要得到一个正方形,剪口与折痕应成多少度的角
20. 如图,为了做一个无盖纸盒,小明先在一块矩形硬纸板的四角画出四个相同的正方形,用剪刀剪下,然后把纸板的四边沿虚线折起,并用胶带粘好,一个无盖纸盒就做成了.纸盒的底面是什么形状 为什么
21. 如图,在 中,, 于点 ,, 是斜边的中点. 是多少度 为什么
22. 如图,四边形 是菱形,,, 于点 .求 的长.
23. (1)如图(1),四边形 是矩形,,, 三点的坐标分别是 ,,.求点 的坐标.
(2)如图(2),四边形 是菱形,, 两点的坐标分别是 ,,点 , 在坐标轴上.求 , 两点的坐标.
(3)如图(3),四边形 是正方形,, 两点的坐标分别是 ,.求 , 两点的坐标.
24. 如图,将等腰三角形纸片 沿底边 上的高 剪成两个三角形,用这两个三角形你能拼成多少种平行四边形 试一试,分别求出它们的对角线的长.
25. 如图是一块正方形草地,要在上面修建两条交叉的小路,使得这两条小路将草地分成的四部分面积相等,你有多少种方法 并与你的同学交流一下.
26. 如图,, 平分 ,且交 于点 , 平分 ,且交 于点 ,连接 .求证:四边形 是菱形.
27. 如图,四边形 是菱形,点 , 分别在 , 上,且 ,,;点 , 分别在 , 上, 与 相交于点 .求证:四边形 , 都是菱形.
28. 如图,,,, 分别是正方形 四条边上的点,且 .试判断四边形 是什么图形,并证明你的结论.
29. 如图,四边形 是正方形. 是 上的任意一点, 于点 ,,且交 于点 .求证:.
30. 如图,在 中,, 分别是边 , 上的中线, 与 相交于点 . 与 的长度有什么关系 边上的中线是否一定过点 为什么 (提示:分别作 , 的中点 ,,连接 ,,,.)
答案
1. 如教科书图 ,证明 .
2. ,.
3. 是.它有两条对称轴,分别是对边中点连线所在的直线.
4. 需要再搬来 盆红花.
根据矩形的对角线相等,以及对角线交点处不放花.
需要再搬来 盆红花.根据矩形的对角线相等,以及对角线交点处要放花.
5. .
6. ,.
7. ,.
8. (1) 略;
(2) 略.
9. 这是一个特殊的平行四边形—— 菱形.由勾股定理的逆定理可知,这个平行四边形的对角线互相垂直.面积为 .
10. 它是一个菱形.
可以证明它的四条边相等.
11. (1) 这样得到的是一组邻边相等,并且一个角是直角的平行四边形,因此它是正方形.
(2) 上面(1)中正方形的面积最大.
12. ,.
13. 个都是.它们都符合正方形的判定条件.
14. 是.利用 ,可知 ,从而 ,平行四边形 的对角线相等,它是一个矩形.
15. 由于四边形的内角和为 ,四个角又都相等,
所以它的四个角都是直角.
因此这个四边形是矩形.
16. 能.这时他得到的是一个角为直角的平行四边形,即矩形.
17. ,.
18. (1) 四边形 是菱形,,
,
.
(2) 连接 交 于点 ,
则 ,,
又 ,
在 中,,
,
.
19.
20. 矩形,它的四个角都是直角.
21. .提示:.
22. .
由 可得.
23. (1) ;
(2) ,;
(3) ,.
24. 种.
可以分别以 ,, 为四边形的一条对角线,得到 种平行四边形,
它们的对角线长分别为 ,(或 );,;,(或 ).
25. 分法有无数种.只要保持两条小路互相垂直,并且都过正方形的中心即可.
26. 由 ,可知 ,同理可得 .从而 ,,四边形 是一组邻边相等的平行四边形,它是菱形.
27. 四边形 , 都是一组邻边相等的平行四边形.
28. 正方形.提示:利用 ,证明四边形 的四条边相等,四个角都是直角.
29. 由 ,可得 ,从而 .
30. , 边上的中线一定过点 .
利用四边形 是平行四边形,可知 ;
设 边上的中线和 相交于点 ,可知 ,从而 与 重合.
