平行线2[下学期]
图片预览






文档简介
课件15张PPT。平行线观察:如图5.2—1,分别将木条a、b与木条c钉在一起,并把它们想象成两端可以无限延伸的三条直线。转动a,直线a从在c的左侧与直线b相交逐步变为在右侧与b相交。想象一下,在这个过程中,有没有直线a与直线b不相交的位置呢?定义:在同一个平面内,不相交的两条直线叫做平行线。
请大家想一想,在实际生活中平行线的实例。
在同一平面内两条互不重合的直线的位置关系有哪几种?
相交
平行讨论:在图5.2—1转动木条a的过程中,有几个位置使得a与b平行?如图5.2—3,过点B画直线a的平行线,能画出几条?再过点C画直线a的平行线,它和前面过点B画出的直线平行吗?平行公理:经过直线外一点,有且只有一条直线与这条直线平行。
平行公理的推论:如果两条直线都和第三条直线平行,那么这两条直线也互相平行。
推论的实质:平行线具有传递性。
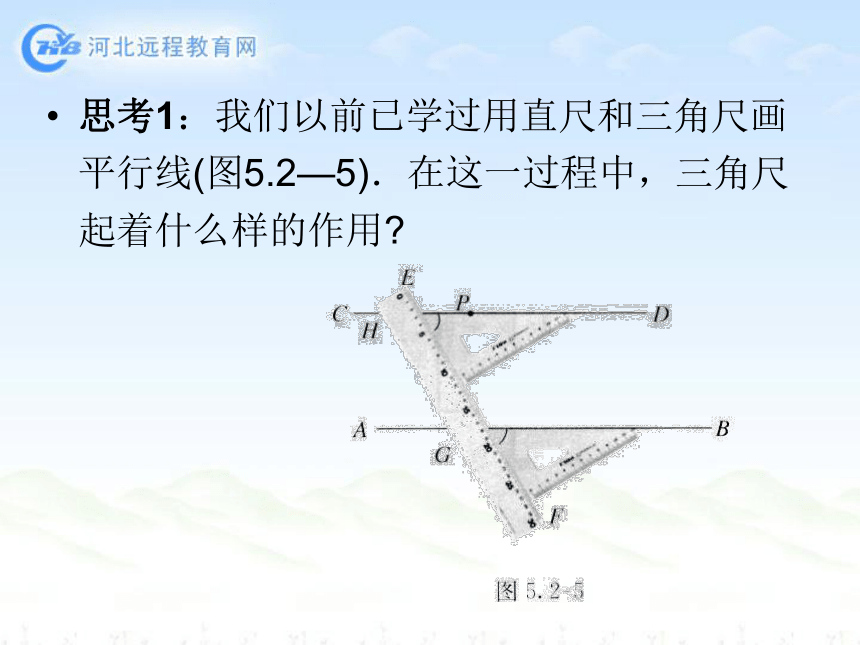
思考1:我们以前已学过用直尺和三角尺画平行线(图5.2—5).在这一过程中,三角尺起着什么样的作用?思考2:如图5.2—8,分别将木条a、b与木条c钉在一起,并把它们想象成直线.在直线a、b被直线c所截成的角中,∠1和∠2是同位角.∠2和∠3有怎样的位置关系?∠2和∠4呢?转动a或b,这些角之间还保持这种关系吗?思考3:如图5.2-9中,如果∠2=∠3,能得出a∥b吗?
同位角相等
内错角相等
同旁内角互补例题1如图,两直线AB、CD被EF所截,
∠1=70 °,下列结论正确的是( )
(A)若∠2= 70 °,则AB∥CD
(B)若∠5= 70 °,则AB∥CD
(C)若∠3= 110 °,则AB∥CD
(D)若∠4= 70 °,则AB∥CD
B 例题2 如图, 已知∠B=25o, ∠BCD=45o, ∠CDE=30o, ∠E=10o.求证:AB∥EF
ABCDEF作CM ∥A B作DN ∥ EFDN ∥ CMMN1234
请大家想一想,在实际生活中平行线的实例。
在同一平面内两条互不重合的直线的位置关系有哪几种?
相交
平行讨论:在图5.2—1转动木条a的过程中,有几个位置使得a与b平行?如图5.2—3,过点B画直线a的平行线,能画出几条?再过点C画直线a的平行线,它和前面过点B画出的直线平行吗?平行公理:经过直线外一点,有且只有一条直线与这条直线平行。
平行公理的推论:如果两条直线都和第三条直线平行,那么这两条直线也互相平行。
推论的实质:平行线具有传递性。
思考1:我们以前已学过用直尺和三角尺画平行线(图5.2—5).在这一过程中,三角尺起着什么样的作用?思考2:如图5.2—8,分别将木条a、b与木条c钉在一起,并把它们想象成直线.在直线a、b被直线c所截成的角中,∠1和∠2是同位角.∠2和∠3有怎样的位置关系?∠2和∠4呢?转动a或b,这些角之间还保持这种关系吗?思考3:如图5.2-9中,如果∠2=∠3,能得出a∥b吗?
同位角相等
内错角相等
同旁内角互补例题1如图,两直线AB、CD被EF所截,
∠1=70 °,下列结论正确的是( )
(A)若∠2= 70 °,则AB∥CD
(B)若∠5= 70 °,则AB∥CD
(C)若∠3= 110 °,则AB∥CD
(D)若∠4= 70 °,则AB∥CD
B 例题2 如图, 已知∠B=25o, ∠BCD=45o, ∠CDE=30o, ∠E=10o.求证:AB∥EF
ABCDEF作CM ∥A B作DN ∥ EFDN ∥ CMMN1234
