13.1 三角形中的边角关系(1) 课件(共29张PPT)
文档属性
| 名称 | 13.1 三角形中的边角关系(1) 课件(共29张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-10 14:15:44 | ||
图片预览








文档简介
(共29张PPT)
沪科版 八年级上册
13.1 三角形中的边角关系(1)
教学目标
1.了解三角形的概念,掌握分类思想.
2.经历探索三角形中的三条边之间的关系,感受几何学中基本图形的内涵.
3.让学生养成有条理的思考的习惯,以及说理有据的意识,体会三角形三边关系在现实生活中的实际价值.
教学重点:了解三角形的分类,弄清三角形三边关系.
教学难点:对两边之差小于第三边的领悟.
动脑想想:
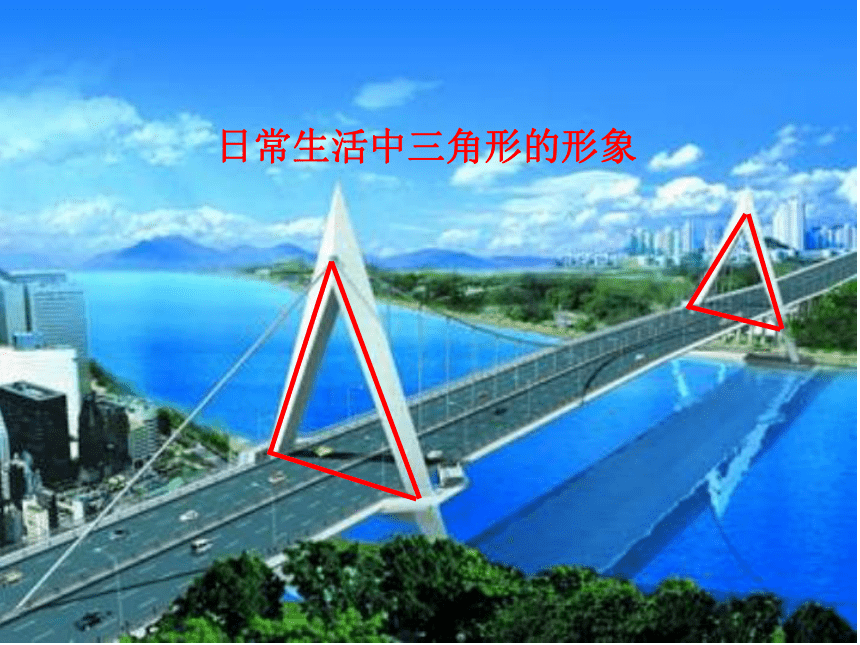
在日常生活中,处处都有三角形的形象,你可以举出实例吗?
日常生活中三角形的形象
日常生活中三角形的形象
日常生活中三角形的形象
日常生活中三角形的形象
由不在同一直线上的三条线段首尾顺次相接所组成的图形叫做三角形.
1.什么叫做三角形?
A
C
B
A
B
学习新知
相邻两边组成的角,叫做三角形的内角,简称三角形的角.
顶点A
顶点B
顶点C
角
角
角
围成三角形的每条线段叫做三角形的边.
每两条线段的交点叫做三角形的顶点.
3.如何表示三角形?
三角形可用符号“△”表示,如下图
三角形ABC记作:△ABC.
读作:三角形ABC
A
C
B
△BAC
△BCA
△CAB
△CBA
△ACB
A
B
C
a
b
c
4.三角形的边可以怎么表示?
如图三角形中三边可表示为AB、BC、AC;
顶点A所对的边BC也可表示为a,
顶点B所对的边AC表示为b,
顶点C所对的边AB表示c.
1.以AB为边的三角形有哪些?
△ABD、
2.以点E为顶点的三角形有哪些?
△ EAB、
A
B
C
D
E
3.图中共有几个三角形?请分别表示出来.
△ ABD、 △ABE、 △ABC、 △ADE、 △ADC、 △AEC.
△ABE、
△ABC.
△EAD、
△EAC.
练习巩固
图中有几个三角形?用符号表示这些三角形.
A
B
C
D
E
△ABE、
△ABC、
△EBC、
△DEC.
△DBC、
图中有5个三角形. 这些三角形分别是:
练习巩固
如图所示的三角形中,假设有一只小虫要从点B出发,沿着三角形的边爬到点C,它有几条路线可以选择?各条路线的长一样吗?
A
B
C
路线1:
路线2:
两条路线长分别是
由“两点之间,线段最短”可以得到
同理可得:AC+BC>
三角形三边关系:
BC,
AB+AC.
AB+AC>BC
AB+BC>
三角形两边的和大于第三边.
由点B到点C.
由点B到点A,再由点A到点C.
AB,
AC.
探究新知
A
B
C
由AC+BC>AB可得:
三角形三边之间的关系:
三角形两边的差小于第三边.
AB-AC由AB+BC>AC可得:
AC-AB下列长度的三条线段能否组成三角形?为什么?
(1)3 , 4, 8 (2)5 , 6, 11 (3)5 , 6, 10.
解:(1)不能组成三角形,
(2)不能组成三角形,
(3)能组成三角形,
解题技巧:较短两线段之和 > 最长线段
因为3+4<8,
即两条线段的和
小于第三条线段,
所以不能组成三角形.
因为5+6=11,
即两条线段的和
等于第三条线段,
所以不能组成三角形.
因为任意两条线段的和都大于
第三条线段.
例题解析
(2) 2, 4, 7 ( )
(4) 4, 5, 7 ( )
(3) 2,5, 7 ( )
1.下列长度的三条线段能否组成三角形?为什么?
(1) 2,5,6 ( )
(2) 3,5,8 ( )
能
不能
2.有长为2cm,4cm , 5cm , 7cm的四根木条,任意选其中三根组成三角形,他能组成几个三角形?
(1) 2, 4, 5 ( )
√
×
√
答:能组成2个三角形.
×
练习巩固
三角形三边之间的关系:
三角形两边的和大于第三边.
三角形三边之间的关系:
三角形两边的差
第三边
三角形两边的差小于第三边.
三角形两边的和
<
第三边小于三角形两边的和.
<
第三边大于三角形两边的差.
AB-AC <
BC
< AB+AC
探究新知
1. 若三角形两边a和b边长分别是4、5,则第三
边c的长度取值范围是( )
A. 12.若一个三角形的两边长是9和4且周长是偶数,则第三边长可能是( )
A.5 B.7 C.8 D.13
3.如果一个三角形的两边长分别是2cm和7cm,
且第三边为奇数,则三角形的周长是___ cm.
A
16
B
练习巩固
有两条边相等的三角形叫做等腰三角形.
三条边都相等的三角形叫做等边三角形.
在等腰三角形中,相等的两边都叫做腰,另一边叫做底,
两腰的夹角叫做顶角,
等边三角形是特殊的等腰三角形,
即底边和腰相等的
等腰三角形.
腰
腰
底
顶角
底角
底角
腰和底边的夹角叫底角.
三边都不相等的三角形
等腰三角形
三角形的分类
只有两条边相等的等腰三角形
等边三角形
按边分
学习新知
用一条长为18厘米的细绳围成一个等腰三角形.
①如果腰长是底边的2倍,那么各边的长是多少?
②能围成有一边的长为4厘米的等腰三角形吗?
为什么
解:①设底边长为x厘米,则腰长为2x厘米
解得 x= 3.6
∴三边长分别为3.6厘米,7.2厘米,7.2厘米.
x
2x
+
+
2x
=18
用一条长为18厘米的细绳围成一个等腰三角形.
②能围成有一边的长为4厘米的等腰三角形吗?为什么
②当4厘米长为底边,设腰长为x厘米,
则4+2x=18,
∴等腰三角形的三边长为7cm、7cm、4cm.
当4厘米长为腰长,设底边长为x厘米,可得
4×2+x=18,
∵4+4<10
综上所述:可以围成底边长是4厘米的等腰三角形.
解得x=7.
解得x=10,
∴此时构不成三角形
②当4厘米长为底边,设腰长为x厘米,
则4+2x=18,解得x=7.
∴等腰三角形的三边长为7cm、7cm、4cm.
当4厘米长为腰长,设底边长为x厘米,可得
4×2+x=18,解得x=10,
∵4+4﹤10∴此时构不成三角形
解:①设底边长为x厘米,则腰长为2x厘米
x+2x+2x=18 解得x=3.6
∴三边长分别为3.6厘米,7.2厘米,7.2厘米。
综上所述:可以围成底边长是4厘米的等腰三角形.
用一条长为18厘米的细绳围成一个等腰三角形.
①如果腰长是底边的2倍,那么各边的长是多少?
②能围成有一边的长为4厘米的等腰三角形吗?为什么
(1)已知等腰三角形的一边等于7,一边等于8,则它的周长为 .
(2)已知等腰三角形的一边等于6,一边等于13,则它的周长为 .
22或23
32
巩固提高
3.现有两根木棒,它们长分别是40㎝和50㎝,若要钉成一个三角形木架,则下列四根木棒应选取( )
A.10㎝ 的木棒 B.40㎝的木棒
C.90㎝的木棒 D.100㎝的木棒
4.以长为2㎝,3㎝,5㎝,7㎝的四条线段中的的三条线段为边,可以画出的三角形的个数为( )
A. 1个 B. 2个 C. 2个 D. 0个
B
A
今天作业
课本P73页第1题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
沪科版 八年级上册
13.1 三角形中的边角关系(1)
教学目标
1.了解三角形的概念,掌握分类思想.
2.经历探索三角形中的三条边之间的关系,感受几何学中基本图形的内涵.
3.让学生养成有条理的思考的习惯,以及说理有据的意识,体会三角形三边关系在现实生活中的实际价值.
教学重点:了解三角形的分类,弄清三角形三边关系.
教学难点:对两边之差小于第三边的领悟.
动脑想想:
在日常生活中,处处都有三角形的形象,你可以举出实例吗?
日常生活中三角形的形象
日常生活中三角形的形象
日常生活中三角形的形象
日常生活中三角形的形象
由不在同一直线上的三条线段首尾顺次相接所组成的图形叫做三角形.
1.什么叫做三角形?
A
C
B
A
B
学习新知
相邻两边组成的角,叫做三角形的内角,简称三角形的角.
顶点A
顶点B
顶点C
角
角
角
围成三角形的每条线段叫做三角形的边.
每两条线段的交点叫做三角形的顶点.
3.如何表示三角形?
三角形可用符号“△”表示,如下图
三角形ABC记作:△ABC.
读作:三角形ABC
A
C
B
△BAC
△BCA
△CAB
△CBA
△ACB
A
B
C
a
b
c
4.三角形的边可以怎么表示?
如图三角形中三边可表示为AB、BC、AC;
顶点A所对的边BC也可表示为a,
顶点B所对的边AC表示为b,
顶点C所对的边AB表示c.
1.以AB为边的三角形有哪些?
△ABD、
2.以点E为顶点的三角形有哪些?
△ EAB、
A
B
C
D
E
3.图中共有几个三角形?请分别表示出来.
△ ABD、 △ABE、 △ABC、 △ADE、 △ADC、 △AEC.
△ABE、
△ABC.
△EAD、
△EAC.
练习巩固
图中有几个三角形?用符号表示这些三角形.
A
B
C
D
E
△ABE、
△ABC、
△EBC、
△DEC.
△DBC、
图中有5个三角形. 这些三角形分别是:
练习巩固
如图所示的三角形中,假设有一只小虫要从点B出发,沿着三角形的边爬到点C,它有几条路线可以选择?各条路线的长一样吗?
A
B
C
路线1:
路线2:
两条路线长分别是
由“两点之间,线段最短”可以得到
同理可得:AC+BC>
三角形三边关系:
BC,
AB+AC.
AB+AC>BC
AB+BC>
三角形两边的和大于第三边.
由点B到点C.
由点B到点A,再由点A到点C.
AB,
AC.
探究新知
A
B
C
由AC+BC>AB可得:
三角形三边之间的关系:
三角形两边的差小于第三边.
AB-AC
AC-AB
(1)3 , 4, 8 (2)5 , 6, 11 (3)5 , 6, 10.
解:(1)不能组成三角形,
(2)不能组成三角形,
(3)能组成三角形,
解题技巧:较短两线段之和 > 最长线段
因为3+4<8,
即两条线段的和
小于第三条线段,
所以不能组成三角形.
因为5+6=11,
即两条线段的和
等于第三条线段,
所以不能组成三角形.
因为任意两条线段的和都大于
第三条线段.
例题解析
(2) 2, 4, 7 ( )
(4) 4, 5, 7 ( )
(3) 2,5, 7 ( )
1.下列长度的三条线段能否组成三角形?为什么?
(1) 2,5,6 ( )
(2) 3,5,8 ( )
能
不能
2.有长为2cm,4cm , 5cm , 7cm的四根木条,任意选其中三根组成三角形,他能组成几个三角形?
(1) 2, 4, 5 ( )
√
×
√
答:能组成2个三角形.
×
练习巩固
三角形三边之间的关系:
三角形两边的和大于第三边.
三角形三边之间的关系:
三角形两边的差
第三边
三角形两边的差小于第三边.
三角形两边的和
<
第三边小于三角形两边的和.
<
第三边大于三角形两边的差.
AB-AC <
BC
< AB+AC
探究新知
1. 若三角形两边a和b边长分别是4、5,则第三
边c的长度取值范围是( )
A. 1
A.5 B.7 C.8 D.13
3.如果一个三角形的两边长分别是2cm和7cm,
且第三边为奇数,则三角形的周长是___ cm.
A
16
B
练习巩固
有两条边相等的三角形叫做等腰三角形.
三条边都相等的三角形叫做等边三角形.
在等腰三角形中,相等的两边都叫做腰,另一边叫做底,
两腰的夹角叫做顶角,
等边三角形是特殊的等腰三角形,
即底边和腰相等的
等腰三角形.
腰
腰
底
顶角
底角
底角
腰和底边的夹角叫底角.
三边都不相等的三角形
等腰三角形
三角形的分类
只有两条边相等的等腰三角形
等边三角形
按边分
学习新知
用一条长为18厘米的细绳围成一个等腰三角形.
①如果腰长是底边的2倍,那么各边的长是多少?
②能围成有一边的长为4厘米的等腰三角形吗?
为什么
解:①设底边长为x厘米,则腰长为2x厘米
解得 x= 3.6
∴三边长分别为3.6厘米,7.2厘米,7.2厘米.
x
2x
+
+
2x
=18
用一条长为18厘米的细绳围成一个等腰三角形.
②能围成有一边的长为4厘米的等腰三角形吗?为什么
②当4厘米长为底边,设腰长为x厘米,
则4+2x=18,
∴等腰三角形的三边长为7cm、7cm、4cm.
当4厘米长为腰长,设底边长为x厘米,可得
4×2+x=18,
∵4+4<10
综上所述:可以围成底边长是4厘米的等腰三角形.
解得x=7.
解得x=10,
∴此时构不成三角形
②当4厘米长为底边,设腰长为x厘米,
则4+2x=18,解得x=7.
∴等腰三角形的三边长为7cm、7cm、4cm.
当4厘米长为腰长,设底边长为x厘米,可得
4×2+x=18,解得x=10,
∵4+4﹤10∴此时构不成三角形
解:①设底边长为x厘米,则腰长为2x厘米
x+2x+2x=18 解得x=3.6
∴三边长分别为3.6厘米,7.2厘米,7.2厘米。
综上所述:可以围成底边长是4厘米的等腰三角形.
用一条长为18厘米的细绳围成一个等腰三角形.
①如果腰长是底边的2倍,那么各边的长是多少?
②能围成有一边的长为4厘米的等腰三角形吗?为什么
(1)已知等腰三角形的一边等于7,一边等于8,则它的周长为 .
(2)已知等腰三角形的一边等于6,一边等于13,则它的周长为 .
22或23
32
巩固提高
3.现有两根木棒,它们长分别是40㎝和50㎝,若要钉成一个三角形木架,则下列四根木棒应选取( )
A.10㎝ 的木棒 B.40㎝的木棒
C.90㎝的木棒 D.100㎝的木棒
4.以长为2㎝,3㎝,5㎝,7㎝的四条线段中的的三条线段为边,可以画出的三角形的个数为( )
A. 1个 B. 2个 C. 2个 D. 0个
B
A
今天作业
课本P73页第1题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
