13.1 三角形中的边角关系(2) 课件(共19张PPT)
文档属性
| 名称 | 13.1 三角形中的边角关系(2) 课件(共19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 931.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-10 14:16:47 | ||
图片预览


文档简介
(共19张PPT)
沪科版 八年级上册
13.1 三角形中的边角关系(2)
教学目标
1. 掌握三角形的内角和定理,能应用三角形内角和定理解决一些简单的实际问题.
2. 经历实验活动的过程,得出三角形的内角和定理.
3. 通过积极思考、踊跃发言,养成良好的学习习惯.通过生动有趣的教学活动,发展学生的合情推理能力和丰富的情感态度,提高学生学习数学的兴趣.
教学重点:三角形内角和定理.
教学难点:三角形内角和定理的推理的过程.
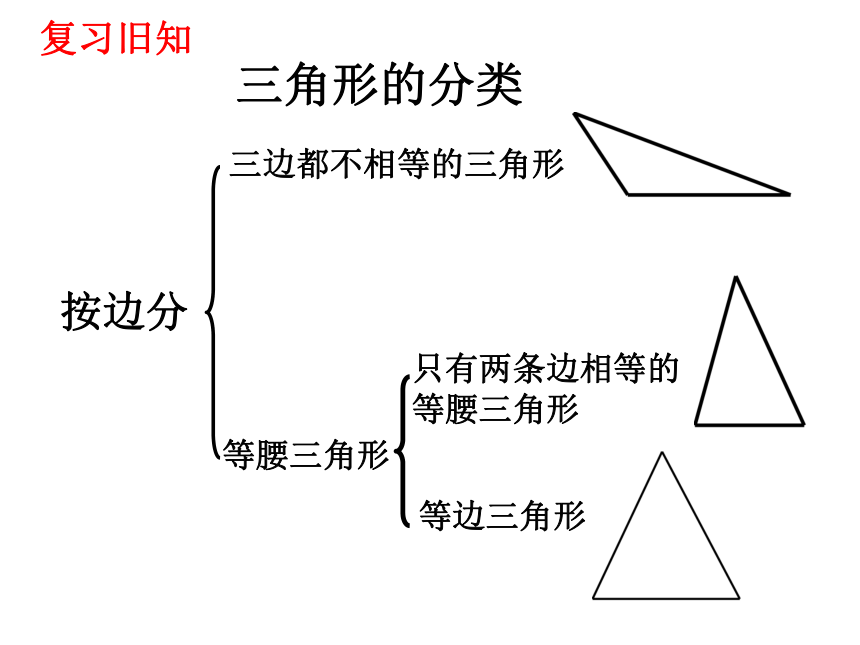
三边都不相等的三角形
等腰三角形
三角形的分类
只有两条边相等的等腰三角形
等边三角形
按边分
复习旧知
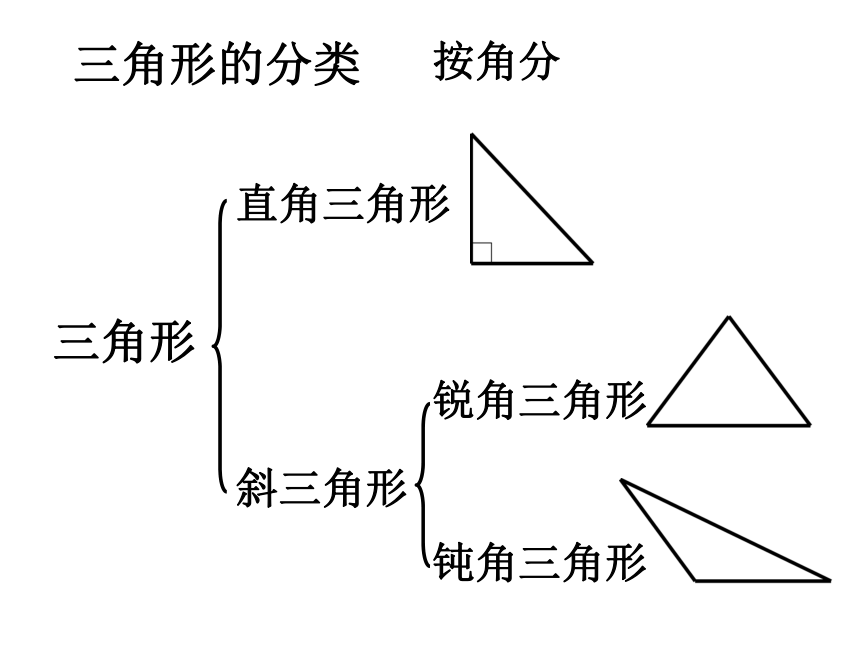
锐角三角形
直角三角形
钝角三角形
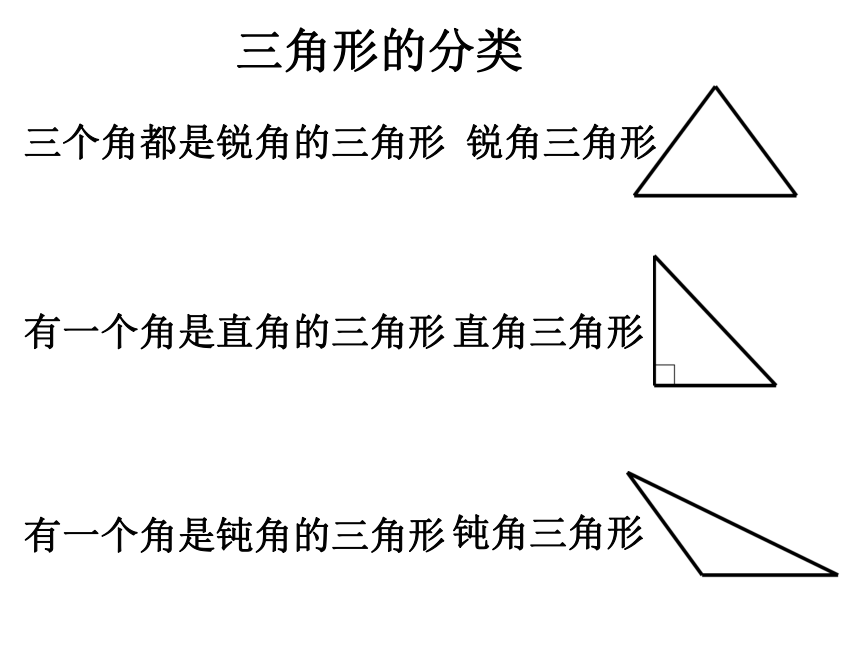
三角形的分类
三个角都是锐角的三角形
有一个角是直角的三角形
有一个角是钝角的三角形
锐角三角形
直角三角形
钝角三角形
三角形的分类
按角分
三角形
斜三角形
直角三角形
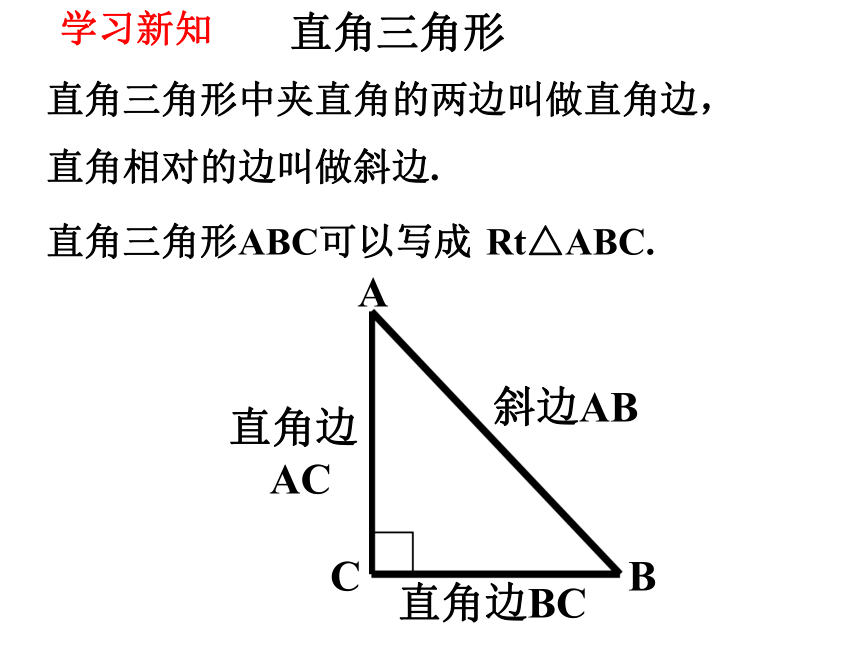
直角边
AC
直角边BC
斜边AB
直角三角形中夹直角的两边叫做直角边,
直角相对的边叫做斜边.
直角三角形ABC可以写成
Rt△ABC.
A
B
C
学习新知
在一个三角形中,三个内角之间有什么关系?
A
B
C
∠A+∠B+∠C=180°.
三角形的内角和等于180°.
学习新知
例2 已知: △ ABC中,BD⊥ AC,垂足为D, ∠ABD=54°, ∠DBC=18°.求∠A和∠C的度数.
D
A
B
C
解:
∵ BD⊥ AC,
∴∠ADB= ∠BDC=90°.
在△ ABD中,
∠A+∠ABD+∠ADB=180°.
∴∠A=180°-∠ABD-∠ADB.
∵∠ABD=54°, ∠ADB=90°,
∴∠A=180°-54°-90°
=36°.
例题解析
例2 已知: △ ABC中,BD⊥ AC,垂足为D, ∠ABD=54°, ∠DBC=18°.求∠A和∠C的度数.
在△ Rt△BDC中,
∠C+∠BDC+∠DBC=180°.
∴∠C=180°-∠BDC-∠DBC.
∵∠BDC=90°, ∠DBC=18°,
∴∠C=180°-90°-18°
=72°.
D
A
B
C
(1)已知:∠A=105°,∠B-∠C=15°,
则∠C= ;
1.△ ABC中:
(2)已知:∠A:∠B:∠C=3: 4: 5,
则∠C= ;
∠B+∠C=75°.
30°
3x
3x
75°
x=15°
4x
5x
+ + =180°.
练习巩固
2 . 已知:如图, △ ABC中,∠ACB=90°, CD⊥ AB,垂足为D.
(1)写出图中所有相等的角;
(2)写出图中所有的直角三角形,并指出它们的斜边.
A
B
C
D
(1)图中相等的角有:
∠ACB= ∠BDC=∠ADC=90°.
∠A=∠BCD,
∠B=∠ACD.
2 . 已知:如图, △ ABC中,∠ACB=90°, CD⊥ AB,垂足为D.
(2)写出图中所有的直角三角形,并指出它们的斜边.
A
B
C
D
(2)图中的直角三角形有:
Rt△ACB,
它的斜边为AB.
Rt△ADC,
它的斜边为AC.
Rt△BDC,
它的斜边为BC.
3.已知: 如图,在△ ABC中,AD⊥ BC,垂足为D, ∠B=70°, ∠BAC=46°.求∠CAD的度数.
D
A
B
C
AD⊥ BC
∠ADB= 90°
∠BAD
∠CAD
3.已知: 如图,在△ ABC中,AD⊥ BC,垂足为D, ∠B=70°, ∠BAC=46°.求∠CAD的度数.
D
A
B
C
解:
∵ AD⊥ BC,
∴∠ADB= 90°.
△ ABD中,
∠B+∠BAD+∠ADB=180°.
∴∠BAD=180°-∠B-∠ADB.
∵∠B=70°, ∠ADB=90°,
∴∠BAD=180°-70°-90°
=20°.
∵∠BAC=46°,
∴∠CAD=∠BAC-∠BAD
=46°-20°
=26°.
4.在一个三角形中,最多只可能有一个直角
或钝角,为什么?
答:如果有两个直角或钝角,就会出现三角形内角和大于180°的情况,这就与三角形是180°相矛盾,所以在一个三角形中,最多只可能有一个直角或钝角.
5.已知: △ ABC中,AB=5,BC=2a + 1,
AC=12. 求a的范围.
解:
BC
AC-AB
AC+AB
BC
12-5
12+5
<
<
<
<
2a + 1
7
17
<
<
2a
<
7-1
17-1
<
2a
<
6
16
<
a
<
3
8
<
今天作业
课本P74页第2、3 题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
沪科版 八年级上册
13.1 三角形中的边角关系(2)
教学目标
1. 掌握三角形的内角和定理,能应用三角形内角和定理解决一些简单的实际问题.
2. 经历实验活动的过程,得出三角形的内角和定理.
3. 通过积极思考、踊跃发言,养成良好的学习习惯.通过生动有趣的教学活动,发展学生的合情推理能力和丰富的情感态度,提高学生学习数学的兴趣.
教学重点:三角形内角和定理.
教学难点:三角形内角和定理的推理的过程.
三边都不相等的三角形
等腰三角形
三角形的分类
只有两条边相等的等腰三角形
等边三角形
按边分
复习旧知
锐角三角形
直角三角形
钝角三角形
三角形的分类
三个角都是锐角的三角形
有一个角是直角的三角形
有一个角是钝角的三角形
锐角三角形
直角三角形
钝角三角形
三角形的分类
按角分
三角形
斜三角形
直角三角形
直角边
AC
直角边BC
斜边AB
直角三角形中夹直角的两边叫做直角边,
直角相对的边叫做斜边.
直角三角形ABC可以写成
Rt△ABC.
A
B
C
学习新知
在一个三角形中,三个内角之间有什么关系?
A
B
C
∠A+∠B+∠C=180°.
三角形的内角和等于180°.
学习新知
例2 已知: △ ABC中,BD⊥ AC,垂足为D, ∠ABD=54°, ∠DBC=18°.求∠A和∠C的度数.
D
A
B
C
解:
∵ BD⊥ AC,
∴∠ADB= ∠BDC=90°.
在△ ABD中,
∠A+∠ABD+∠ADB=180°.
∴∠A=180°-∠ABD-∠ADB.
∵∠ABD=54°, ∠ADB=90°,
∴∠A=180°-54°-90°
=36°.
例题解析
例2 已知: △ ABC中,BD⊥ AC,垂足为D, ∠ABD=54°, ∠DBC=18°.求∠A和∠C的度数.
在△ Rt△BDC中,
∠C+∠BDC+∠DBC=180°.
∴∠C=180°-∠BDC-∠DBC.
∵∠BDC=90°, ∠DBC=18°,
∴∠C=180°-90°-18°
=72°.
D
A
B
C
(1)已知:∠A=105°,∠B-∠C=15°,
则∠C= ;
1.△ ABC中:
(2)已知:∠A:∠B:∠C=3: 4: 5,
则∠C= ;
∠B+∠C=75°.
30°
3x
3x
75°
x=15°
4x
5x
+ + =180°.
练习巩固
2 . 已知:如图, △ ABC中,∠ACB=90°, CD⊥ AB,垂足为D.
(1)写出图中所有相等的角;
(2)写出图中所有的直角三角形,并指出它们的斜边.
A
B
C
D
(1)图中相等的角有:
∠ACB= ∠BDC=∠ADC=90°.
∠A=∠BCD,
∠B=∠ACD.
2 . 已知:如图, △ ABC中,∠ACB=90°, CD⊥ AB,垂足为D.
(2)写出图中所有的直角三角形,并指出它们的斜边.
A
B
C
D
(2)图中的直角三角形有:
Rt△ACB,
它的斜边为AB.
Rt△ADC,
它的斜边为AC.
Rt△BDC,
它的斜边为BC.
3.已知: 如图,在△ ABC中,AD⊥ BC,垂足为D, ∠B=70°, ∠BAC=46°.求∠CAD的度数.
D
A
B
C
AD⊥ BC
∠ADB= 90°
∠BAD
∠CAD
3.已知: 如图,在△ ABC中,AD⊥ BC,垂足为D, ∠B=70°, ∠BAC=46°.求∠CAD的度数.
D
A
B
C
解:
∵ AD⊥ BC,
∴∠ADB= 90°.
△ ABD中,
∠B+∠BAD+∠ADB=180°.
∴∠BAD=180°-∠B-∠ADB.
∵∠B=70°, ∠ADB=90°,
∴∠BAD=180°-70°-90°
=20°.
∵∠BAC=46°,
∴∠CAD=∠BAC-∠BAD
=46°-20°
=26°.
4.在一个三角形中,最多只可能有一个直角
或钝角,为什么?
答:如果有两个直角或钝角,就会出现三角形内角和大于180°的情况,这就与三角形是180°相矛盾,所以在一个三角形中,最多只可能有一个直角或钝角.
5.已知: △ ABC中,AB=5,BC=2a + 1,
AC=12. 求a的范围.
解:
BC
AC-AB
AC+AB
BC
12-5
12+5
<
<
<
<
2a + 1
7
17
<
<
2a
<
7-1
17-1
<
2a
<
6
16
<
a
<
3
8
<
今天作业
课本P74页第2、3 题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
