13.2 命题与证明(3) 课件(共22张PPT)
文档属性
| 名称 | 13.2 命题与证明(3) 课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 993.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-10 00:00:00 | ||
图片预览








文档简介
(共22张PPT)
沪科版 八年级上册
13.2 命题与证明(3)
教学目标
1.认识证明的必要性,初步了解证明的基本步骤和书写格式;
2.培养学生的推理意识,能清晰、有条理的表达自己的思考过程,做到言之有理;
3.经历观察、验证、归纳等过程,能进行简单的证明;
4.体验数学学习充满了探索和创造、感受证明的必要性,养成对数学的好奇性、求知欲和探索创新精神。
教学重点:将文字命题转化为数学问题并进行证明,证明过程中规范性语言的使用。
教学难点:如何正确写出“已知”、“求证”是本节课的难点。
1.什么是命题?
对某一件事情作出正确或不正确判断的句子叫命题.
2.命题的结构是什么?
数学命题通常是由题设和结论两部分组成的.
请同学们判断下列命题哪些是真命题?哪些是假命题?
1.在同一平面内,如果一条直线垂直于两条平行
线中的一条,那么也垂直于另一条. ( )
2.如果两个角互补,那么它们是邻补角. ( )
3.经过直线外一点有且只有一条直线与这条直线
平行. ( )
真
假
真
请同学们判断下列命题哪些是真命题?哪些是假命题?
4.两点确定一条直线. ( )
5.相等的角是对顶角. ( )
6.两条直线被第三条直线所截,如果同位角相等,那么内错角也相等. ( )
真
假
真
从已知条件出发,根据定义、基本事实、已证定理,并根据逻辑规则,推导出结论的方法叫“演绎推理”.演绎推理的过程,叫做演绎证明,简称证明.
什么叫做证明?
如何判断一个命题的真假?
要判断一个命题是真命题需要推理论证;要判断一个命题是假命题只要举出一个反例即可.
创设情境,引入新知
1.辨一辨
直觉的不可靠,证明有必要
长方形的边是曲的
还是直的
a
b
c
d
a、b、c、d这组线是平行线还是相交线
2.当n=0,1,2,3,4时,代数式n2-3n+7的值分别是7,5,5,7,11,它们都是素数,那么,命题“对于自然数n,代数式n2-3n+7的值都是素数”是真命题吗?
创设情境,引入新知
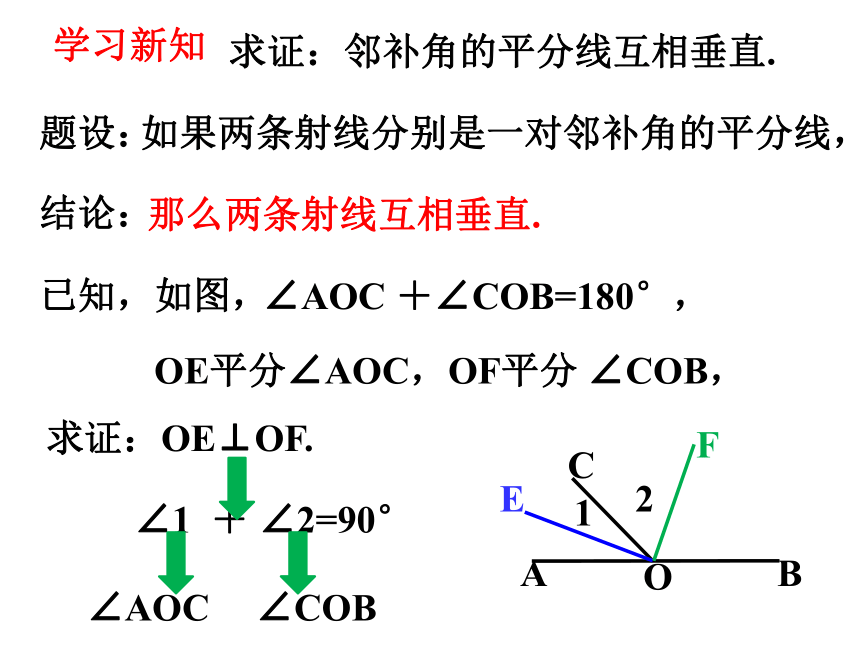
求证:邻补角的平分线互相垂直.
题设:
结论:
那么两条射线互相垂直.
如果两条射线分别是一对邻补角的平分线,
A
B
C
O
已知,如图,
OE平分∠AOC,OF平分 ∠COB,
E
F
求证:
OE⊥OF.
1
2
∠1 + ∠2=90°
∠AOC
∠COB
∠AOC +∠COB=180°,
学习新知
证明:
∵ OE平分 ∠ AOC,
∴∠1= ∠AOC,
∠2= ∠COB.
OF平分 ∠COB,
= ∠AOC + ∠COB
= (∠AOC+∠COB)
∵∠AOC+∠COB=180°,
∴∠1+∠2
= ×180°
= 90°
已知,如图,
∠ AOC和∠COB是一对邻补角,
OE平分∠AOC,OF平分 ∠COB,
求证:
OE⊥OF.
∴OE⊥OF.
1
2
1
2
1
2
1
2
1
2
1
2
A
B
C
O
F
E
1
2
(已知)
(角平分线定义)
(已知)
(等式性质)
(垂直的定义)
=∠EOF
∴∠1+∠2
(等量代换)
1.如图,BC⊥ AC于点C,CD⊥AB于点D, ∠EBC=∠A,求证: BE∥CD.
∠BCD=∠EBC
E
B
A
C
D
要证: BE∥CD
∠BCD=∠A
∠BCD+∠ACD=90°
∠A+∠ACD=90°
BC⊥AC
CD⊥AB
例题解析
证明:∵BC⊥AC,( )
∴ .(垂直的定义)
∵ ,(已知)
∴∠A+∠ACD=90°.( )
∴ .( )
又∵∠EBC=∠A,( )
∴∠EBC=∠BCD,( )
∴BE∥CD.( )
∠BCD=∠A,
∠BCA=∠BCD+∠ACD=90°
CD⊥AB
已知
∴∠ADC=90°.
(垂直的定义)
已知
等式性质
内错角相等,两直线平行
同角的余角相等
三角形内角和
E
B
A
C
D
2.已知,如图,AB⊥BF, CD⊥BF,
∠1=∠2 . 求证: ∠3=∠4.
1
2
3
4
A
B
C
D
E
F
要证: ∠3=∠4
CD//EF
AB//EF
AB//CD
∠1=∠2
∠B=∠CDF
AB⊥BF, CD⊥BF
例题解析
( )
( )
2.已知,如图,AB⊥BF, CD⊥BF, ∠1=∠2 . 求证: ∠3=∠4.
证明:∵ AB⊥BF,CD⊥BF
∴∠B=∠CDF=90°
∴AB//CD.
又∵∠1=∠2,
∴AB//EF.
∴CD//EF.
∴∠3=∠4.
已知
垂直定义
同位角相等,两直线平行
(已知)
( )
平行于同一直线的两直线平行
两直线平行,同位角相等
( )
( )
( )
1
2
3
4
A
B
C
D
E
F
内错角相等,两直线平行
1.已知,如图,
AB∥DC,
AD∥BC.
∠A=∠C.
求证:
证明:
∵AB∥DC,( )
∵AD∥BC.( )
∴∠A+∠D=180°.( )
∴∠C+∠D=180°.( )
∴∠A=∠C.( )
∴∠A+∠D=∠C+∠D.( )
C
A
B
D
已知
两直线平行,同旁内角互补
已知
两直线平行,同旁内角互补
等量代换
等式性质
练习巩固
2.已知,如图,
DC∥AB,
∠1=∠2.
求证:
证明:
∵DC∥AB,( )
∵DF平分∠CDB,( )
∴∠ABD=∠CDB.( )
BE平分∠ABD,( )
∴∠1=∠2.( )
∴∠1= ∠ ,( )
已知
两直线平行,内错角相等
已知
DF平分∠CDB,
BE平分∠ABD,
∠2= ∠ . ( )
1
2
1
2
CDB
已知
角平分线定义
ABD
角平分线定义
等式性质
C
A
B
D
1
2
3.已知,CD⊥AB于D,点F是BC上任意一点,FE⊥AB于E,且∠1=∠2, ∠3 =80°.求∠BCA的度数.
4
∵CD ⊥AB,FE⊥AB,
∴FE∥CD.
∵∠1=∠2,
∴DG∥BC.
∴∠3=∠BCA.
(已知)
(已知)
(内错角相等,两直线平行)
(垂直于同一直线的两直线平行)
(两直线平行,同位角相等)
∴∠2=∠4.
(两直线平行,同位角相等)
∴∠1=∠4.
∵∠3=80°,
(已知)
∴∠BCA =80°.
解:
(等式性质)
(等式性质)
(1)证明的必要性及意义
(2)证明的格式
(3)数学证明题的基本思路:由“因”导
“果”,执“果”索“因”
课堂小结
填空(请你将理由补充完整)
已知:如图1,∠1=∠2,∠3=∠4,求证:EG∥FH.
证明:∵∠1=∠2(已知)
∠AEF=∠1 ( );
∴∠AEF=∠2 ( ).
∴AB∥CD ( ).
∴∠BEF=∠CFE ( ).
∵∠3=∠4(已知);
∴∠BEF-∠4=∠CFE-∠3.
即∠GEF=∠HFE ( ).
∴EG∥FH ( ).
对顶角相等
等式性质
同位角相等,两直线平行
两直线平行,内错角相等
等式性质
内错角相等,两直线平行
今天作业
课本P85页第7、8 题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
沪科版 八年级上册
13.2 命题与证明(3)
教学目标
1.认识证明的必要性,初步了解证明的基本步骤和书写格式;
2.培养学生的推理意识,能清晰、有条理的表达自己的思考过程,做到言之有理;
3.经历观察、验证、归纳等过程,能进行简单的证明;
4.体验数学学习充满了探索和创造、感受证明的必要性,养成对数学的好奇性、求知欲和探索创新精神。
教学重点:将文字命题转化为数学问题并进行证明,证明过程中规范性语言的使用。
教学难点:如何正确写出“已知”、“求证”是本节课的难点。
1.什么是命题?
对某一件事情作出正确或不正确判断的句子叫命题.
2.命题的结构是什么?
数学命题通常是由题设和结论两部分组成的.
请同学们判断下列命题哪些是真命题?哪些是假命题?
1.在同一平面内,如果一条直线垂直于两条平行
线中的一条,那么也垂直于另一条. ( )
2.如果两个角互补,那么它们是邻补角. ( )
3.经过直线外一点有且只有一条直线与这条直线
平行. ( )
真
假
真
请同学们判断下列命题哪些是真命题?哪些是假命题?
4.两点确定一条直线. ( )
5.相等的角是对顶角. ( )
6.两条直线被第三条直线所截,如果同位角相等,那么内错角也相等. ( )
真
假
真
从已知条件出发,根据定义、基本事实、已证定理,并根据逻辑规则,推导出结论的方法叫“演绎推理”.演绎推理的过程,叫做演绎证明,简称证明.
什么叫做证明?
如何判断一个命题的真假?
要判断一个命题是真命题需要推理论证;要判断一个命题是假命题只要举出一个反例即可.
创设情境,引入新知
1.辨一辨
直觉的不可靠,证明有必要
长方形的边是曲的
还是直的
a
b
c
d
a、b、c、d这组线是平行线还是相交线
2.当n=0,1,2,3,4时,代数式n2-3n+7的值分别是7,5,5,7,11,它们都是素数,那么,命题“对于自然数n,代数式n2-3n+7的值都是素数”是真命题吗?
创设情境,引入新知
求证:邻补角的平分线互相垂直.
题设:
结论:
那么两条射线互相垂直.
如果两条射线分别是一对邻补角的平分线,
A
B
C
O
已知,如图,
OE平分∠AOC,OF平分 ∠COB,
E
F
求证:
OE⊥OF.
1
2
∠1 + ∠2=90°
∠AOC
∠COB
∠AOC +∠COB=180°,
学习新知
证明:
∵ OE平分 ∠ AOC,
∴∠1= ∠AOC,
∠2= ∠COB.
OF平分 ∠COB,
= ∠AOC + ∠COB
= (∠AOC+∠COB)
∵∠AOC+∠COB=180°,
∴∠1+∠2
= ×180°
= 90°
已知,如图,
∠ AOC和∠COB是一对邻补角,
OE平分∠AOC,OF平分 ∠COB,
求证:
OE⊥OF.
∴OE⊥OF.
1
2
1
2
1
2
1
2
1
2
1
2
A
B
C
O
F
E
1
2
(已知)
(角平分线定义)
(已知)
(等式性质)
(垂直的定义)
=∠EOF
∴∠1+∠2
(等量代换)
1.如图,BC⊥ AC于点C,CD⊥AB于点D, ∠EBC=∠A,求证: BE∥CD.
∠BCD=∠EBC
E
B
A
C
D
要证: BE∥CD
∠BCD=∠A
∠BCD+∠ACD=90°
∠A+∠ACD=90°
BC⊥AC
CD⊥AB
例题解析
证明:∵BC⊥AC,( )
∴ .(垂直的定义)
∵ ,(已知)
∴∠A+∠ACD=90°.( )
∴ .( )
又∵∠EBC=∠A,( )
∴∠EBC=∠BCD,( )
∴BE∥CD.( )
∠BCD=∠A,
∠BCA=∠BCD+∠ACD=90°
CD⊥AB
已知
∴∠ADC=90°.
(垂直的定义)
已知
等式性质
内错角相等,两直线平行
同角的余角相等
三角形内角和
E
B
A
C
D
2.已知,如图,AB⊥BF, CD⊥BF,
∠1=∠2 . 求证: ∠3=∠4.
1
2
3
4
A
B
C
D
E
F
要证: ∠3=∠4
CD//EF
AB//EF
AB//CD
∠1=∠2
∠B=∠CDF
AB⊥BF, CD⊥BF
例题解析
( )
( )
2.已知,如图,AB⊥BF, CD⊥BF, ∠1=∠2 . 求证: ∠3=∠4.
证明:∵ AB⊥BF,CD⊥BF
∴∠B=∠CDF=90°
∴AB//CD.
又∵∠1=∠2,
∴AB//EF.
∴CD//EF.
∴∠3=∠4.
已知
垂直定义
同位角相等,两直线平行
(已知)
( )
平行于同一直线的两直线平行
两直线平行,同位角相等
( )
( )
( )
1
2
3
4
A
B
C
D
E
F
内错角相等,两直线平行
1.已知,如图,
AB∥DC,
AD∥BC.
∠A=∠C.
求证:
证明:
∵AB∥DC,( )
∵AD∥BC.( )
∴∠A+∠D=180°.( )
∴∠C+∠D=180°.( )
∴∠A=∠C.( )
∴∠A+∠D=∠C+∠D.( )
C
A
B
D
已知
两直线平行,同旁内角互补
已知
两直线平行,同旁内角互补
等量代换
等式性质
练习巩固
2.已知,如图,
DC∥AB,
∠1=∠2.
求证:
证明:
∵DC∥AB,( )
∵DF平分∠CDB,( )
∴∠ABD=∠CDB.( )
BE平分∠ABD,( )
∴∠1=∠2.( )
∴∠1= ∠ ,( )
已知
两直线平行,内错角相等
已知
DF平分∠CDB,
BE平分∠ABD,
∠2= ∠ . ( )
1
2
1
2
CDB
已知
角平分线定义
ABD
角平分线定义
等式性质
C
A
B
D
1
2
3.已知,CD⊥AB于D,点F是BC上任意一点,FE⊥AB于E,且∠1=∠2, ∠3 =80°.求∠BCA的度数.
4
∵CD ⊥AB,FE⊥AB,
∴FE∥CD.
∵∠1=∠2,
∴DG∥BC.
∴∠3=∠BCA.
(已知)
(已知)
(内错角相等,两直线平行)
(垂直于同一直线的两直线平行)
(两直线平行,同位角相等)
∴∠2=∠4.
(两直线平行,同位角相等)
∴∠1=∠4.
∵∠3=80°,
(已知)
∴∠BCA =80°.
解:
(等式性质)
(等式性质)
(1)证明的必要性及意义
(2)证明的格式
(3)数学证明题的基本思路:由“因”导
“果”,执“果”索“因”
课堂小结
填空(请你将理由补充完整)
已知:如图1,∠1=∠2,∠3=∠4,求证:EG∥FH.
证明:∵∠1=∠2(已知)
∠AEF=∠1 ( );
∴∠AEF=∠2 ( ).
∴AB∥CD ( ).
∴∠BEF=∠CFE ( ).
∵∠3=∠4(已知);
∴∠BEF-∠4=∠CFE-∠3.
即∠GEF=∠HFE ( ).
∴EG∥FH ( ).
对顶角相等
等式性质
同位角相等,两直线平行
两直线平行,内错角相等
等式性质
内错角相等,两直线平行
今天作业
课本P85页第7、8 题
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
