24.1.4圆周角 课件(共30张PPT)
文档属性
| 名称 | 24.1.4圆周角 课件(共30张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-09 11:28:25 | ||
图片预览





文档简介
(共30张PPT)
24.1.4圆周角
人教版 九年级上册
教学目标
教学目标:
1. 理解圆周角的概念,会叙述并证明圆周角定理.
2. 掌握圆周角与圆心角的关系并能运用圆周角定
理解决简单的几何问题.
3. 理解掌握圆周角定理的推论及其证明过程.
4. 掌握圆内接多边形的概念及圆内接四边形的性质并能运用其性质进行计算.
回顾复习
1.什么叫圆心角?指出图中的圆心角?
顶点在圆心的角叫圆心角, ∠BOC.
A
在同圆(或等圆)中,如果圆心角、弧、弦有一组量相等,那么它们所对应的其余两个量都分别相等。
2.圆心角、弧、弦之间的关系:
新知讲解
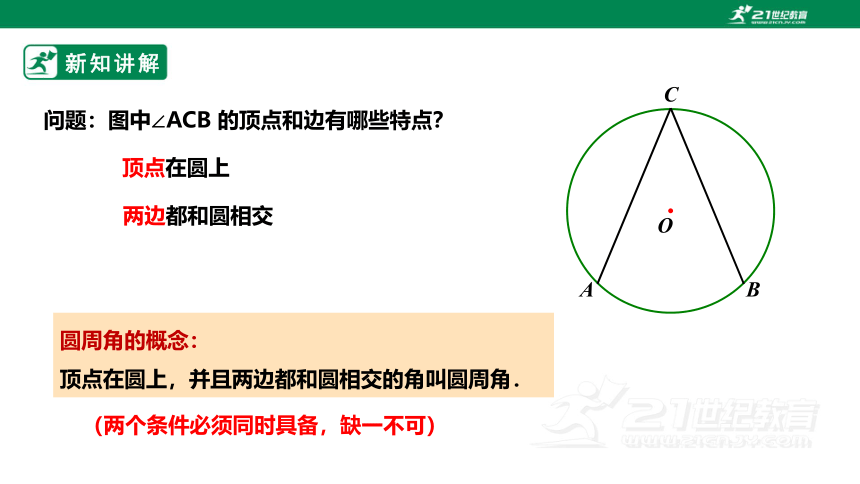
问题:图中∠ACB 的顶点和边有哪些特点?
A
O
B
C
圆周角的概念:
顶点在圆上,并且两边都和圆相交的角叫圆周角.
顶点在圆上
两边都和圆相交
(两个条件必须同时具备,缺一不可)
针对训练
·
C
O
A
B
·
C
O
B
·
C
O
B
A
A
·
C
O
A
B
·
C
O
B
·
C
O
B
A
A
下列各图中的∠BAC是否为圆周角并简述理由.
(2)
(1)
(3)
(5)
(6)
顶点不在圆上
顶点不在圆上
边AC没有和圆相交
√
√
√
新知讲解
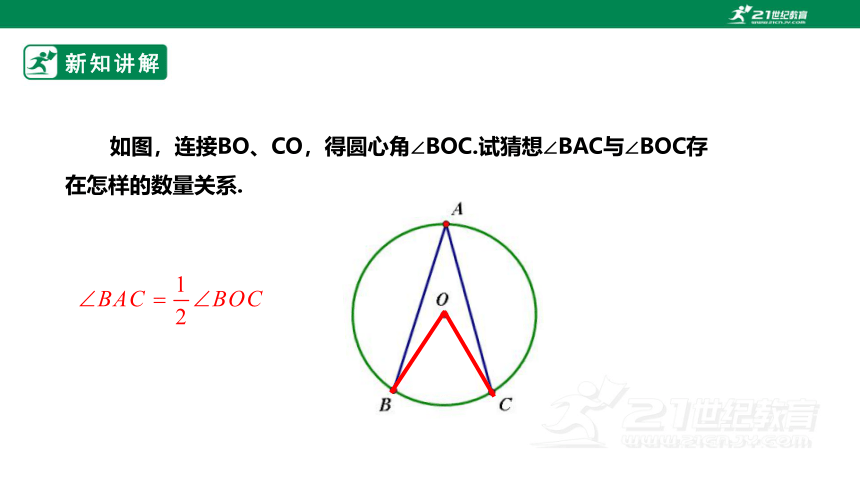
如图,连接BO、CO,得圆心角∠BOC.试猜想∠BAC与∠BOC存在怎样的数量关系.
新知讲解
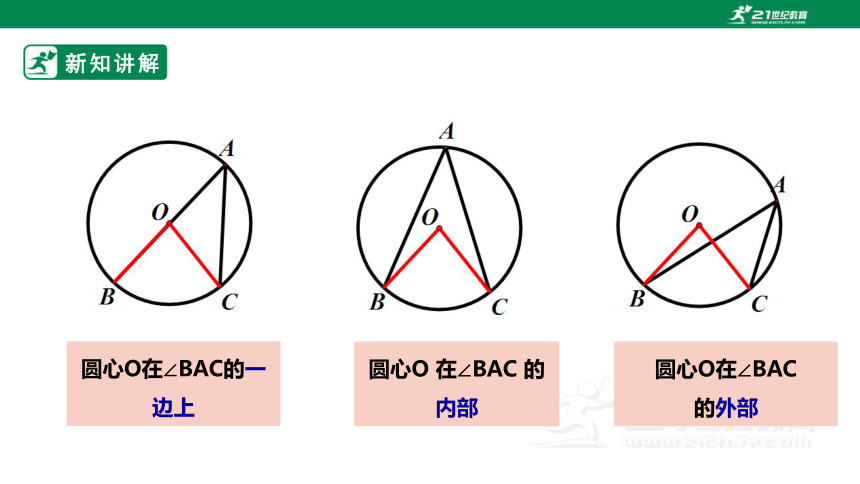
圆心O 在∠BAC 的 内部
圆心O在∠BAC的一边上
圆心O在∠BAC
的外部
新知讲解
圆心O在∠BAC的一边上(特殊情形)
OA=OC
∠A= ∠C
∠BOC= ∠ A+ ∠C
新知讲解
O
A
B
D
O
A
C
D
O
A
B
C
D
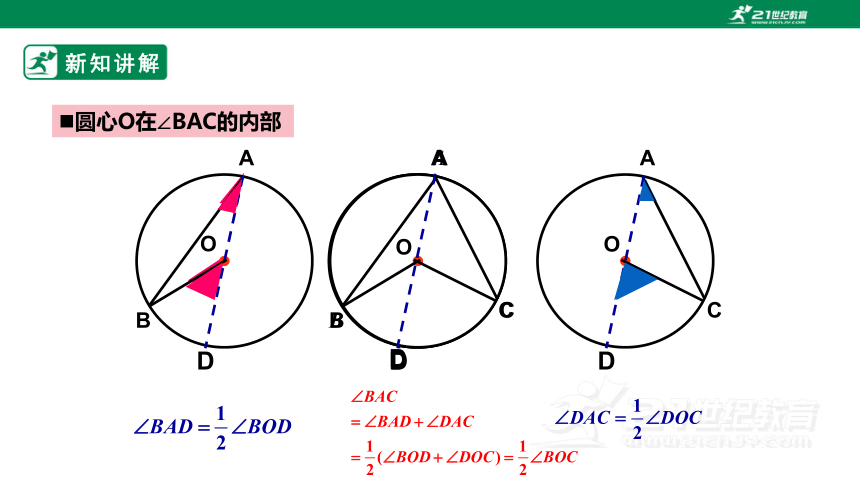
圆心O在∠BAC的内部
O
A
C
D
O
A
B
D
新知讲解
O
A
B
D
C
O
A
D
C
O
A
B
D
C
O
A
D
O
A
B
D
C
O
A
D
O
A
B
D
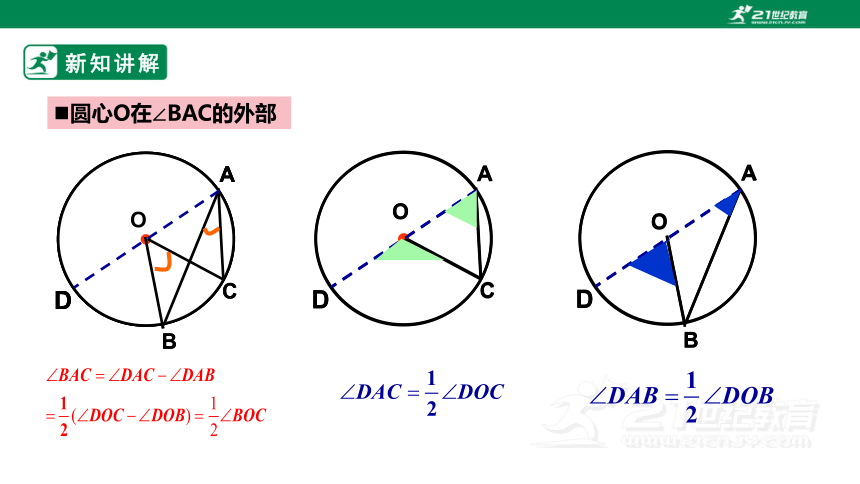
圆心O在∠BAC的外部
新知讲解
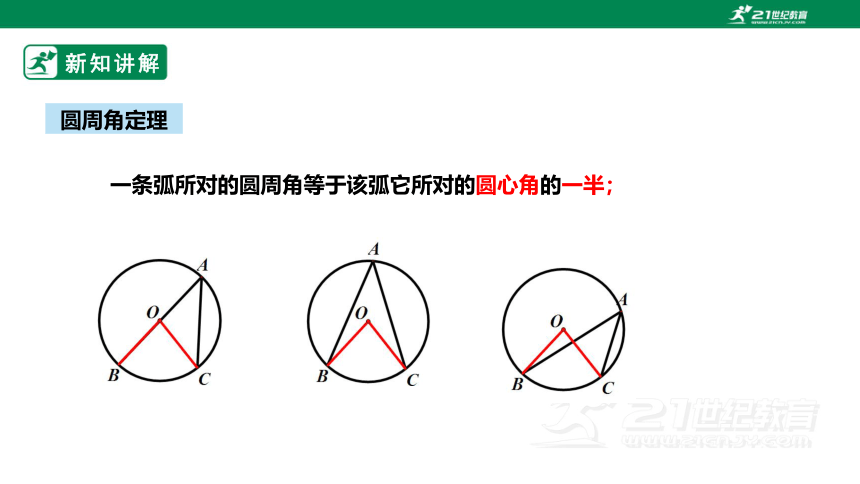
一条弧所对的圆周角等于该弧它所对的圆心角的一半;
圆周角定理
新知讲解
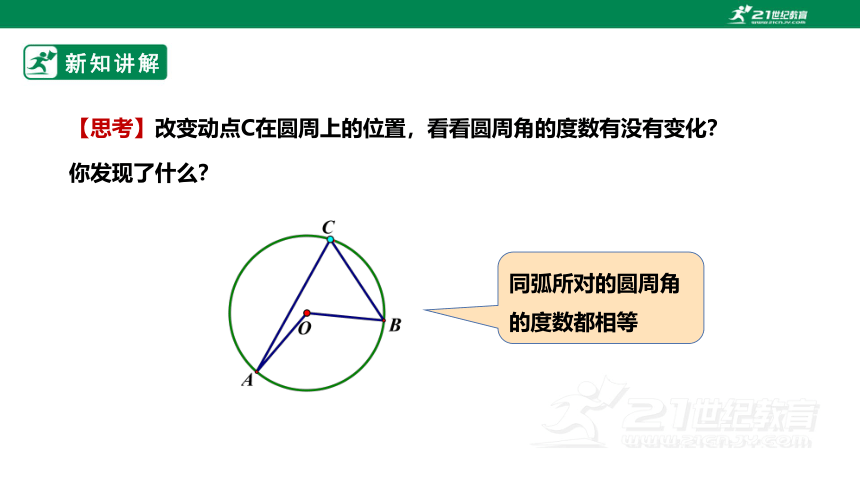
【思考】改变动点C在圆周上的位置,看看圆周角的度数有没有变化?你发现了什么?
同弧所对的圆周角的度数都相等
新知讲解
D
A
B
O
C
E
F
如图,若弧CD=弧EF, ∠A与∠B相等吗?
解:相等
思考:反过来,若∠A=∠B,那么弧CD=弧EF 成立吗?
如果把上述发现的结论中的“同弧”改为“等弧”,结论还正确吗?
∵弧CD=弧EF
新知讲解
如图,BC是⊙O的直径.请问:BC所对的圆周角∠BAC是锐角、直角还是钝角?
∵OA=OB=OC,
∴△AOC、△BOA都是等腰三角形.
∴ ∠OAC=∠OCA,∠OBA=∠OAB.
又∵ ∠OBA+∠OCA+∠CAB=180°,
∴ ∠BAC=∠OAC+∠OAB=180°÷2=90°.
解:∠BAC是直角,理由如下:
连接AO,
若圆周角∠BAC=90°,那么它所对的弦BC经过圆心吗?
新知讲解
半圆(或直径)所对的圆周角是直角,
90°的圆周角所对的弦是直径.
圆周角和直径的关系:
BC是圆O的直径
∠BAC=90°
新知讲解
例4 如图,⊙O的直径AB为10cm,弦AC为6cm. ∠ACB的平分线交⊙O于D. 求BC、AD、BD的长.
解:∵AB是直径,
∴ ∠ACB=∠ADB=90°.
在Rt△ACB中,根据勾股定理得
新知讲解
∵CD平分∠ACB,
∴∠ACD=∠DCB.
∴∠AOD=∠BOD,
∴AD=BD.
在Rt△ABD中,AD2+BD2=AB2,
新知讲解
观察下面的图形,图中的多边形与圆有什么样的位置关系?
如果一个多边形的所有顶点都在同一个圆上,这个多边形叫做圆内接多边形,这个圆叫做这个多边形的外接圆.
新知讲解
如图,四边形ABCD为⊙O的内接四边形,⊙O为四边形ABCD的外接圆.
猜想:∠A与∠C, ∠B与∠D之间的关系为:
∠A+ ∠C=180 ,
∠B+ ∠D=180
想一想:如何证明你的猜想呢?
新知讲解
证明:∵ 弧BCD和弧BAD所对的圆心角的和是周角,
∴∠A+∠C=180°,
同理∠B+∠D=180°,
推论:圆内接四边形的对角互补.
新知讲解
C
O
D
B
A
∵ 弧BCD和弧BAD所对的圆心角的和是周角,
∴∠A+∠C=180°,
同理∠B+∠D=180°,
E
延长BC到点E,有
∠BCD+∠DCE=180°.
∴∠A=∠DCE.
图中∠A与∠DCE的大小有何关系?
推论:圆的内接四边形的任何一个外角都等于它的内对角.
课堂练习
A
B
C
D
O
1.如图,四边形ABCD内接于⊙O,如果∠BOD=130°,则∠BAD的度数是( )
A 115° B 130° C 65° D 50°
A
2.如图,已知BD是⊙O的直径,⊙O的弦AC⊥BD于点E,若∠AOD=60°,则∠DBC的度数为( )
A.30° B.40° C.50° D.60°
A
课堂练习
3.如图,四边形ABCD内接于⊙O,如果∠BOD=130°,则∠BCD的度数是( )
A 115° B 130°
C 65° D 50°
4.如图,等边三角形ABC内接于⊙O,P是AC上的一点,则∠APC= .
A
B
C
D
O
A
B
C
P
C
120°
课堂练习
5.如图,四边形ABCD内接于⊙O,点E在BC的延长线上,若∠BOD=120°,则∠DCE=______°.
60
6.已知△ABC的三个顶点在⊙O上,∠BAC=60°,
∠ABC=45°, 则∠AOB= .
B
A
C
O
150°
课堂练习
7.如图,AB是⊙O的直径,AB=10 cm,∠ADE=60°,DC平∠ADE,求AC,BC的长.
解:∵∠ADE=60°,DC平分∠ADE,
∴∠ADC= ∠ADE=30°,
∴∠ABC=∠ADC=30°.
又∵AB为⊙O的直径,
∴∠ACB=90°,
∴AC= AB=5 cm.
课堂练习
8.如图,AB为⊙O的直径,CF⊥AB于E,交⊙O于D,AF交⊙O于G. 求证:∠FGD=∠ADC.
证明:∵四边形ACDG内接于⊙O,∴∠FGD=∠ACD.
又∵AB为⊙O的直径,CF⊥AB于E,∴AB垂直平分CD,
∴AC=AD,
∴∠ADC=∠ACD,
∴∠FGD=∠ADC.
课堂小结
圆心角
类比
圆周角
圆周角定义
圆周角定理
圆周角定理的推论
圆周角与直
线的关系
1.顶点在圆上,2.两边都与圆相交的角(二者必须同时具备)
半圆或直径所对的圆周角都相等,都等于90°(直角).
在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于该弧所对的圆心角的一半;相等的圆周角所对的弧相等.
1.90°的圆周角所对的弦是直径;
2.圆内接四边形的对角互补.
圆周角
课堂小结
如果一个多边形所有顶点都在同一个圆上,这个多边形叫做圆内接多边形,这个圆叫做这个多边形的外接圆.
圆内接多边形
性质2:圆的内接四边形的任何一个外角都等于它的内对角.
性质1:圆的内接四边形的对角互补.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
24.1.4圆周角
人教版 九年级上册
教学目标
教学目标:
1. 理解圆周角的概念,会叙述并证明圆周角定理.
2. 掌握圆周角与圆心角的关系并能运用圆周角定
理解决简单的几何问题.
3. 理解掌握圆周角定理的推论及其证明过程.
4. 掌握圆内接多边形的概念及圆内接四边形的性质并能运用其性质进行计算.
回顾复习
1.什么叫圆心角?指出图中的圆心角?
顶点在圆心的角叫圆心角, ∠BOC.
A
在同圆(或等圆)中,如果圆心角、弧、弦有一组量相等,那么它们所对应的其余两个量都分别相等。
2.圆心角、弧、弦之间的关系:
新知讲解
问题:图中∠ACB 的顶点和边有哪些特点?
A
O
B
C
圆周角的概念:
顶点在圆上,并且两边都和圆相交的角叫圆周角.
顶点在圆上
两边都和圆相交
(两个条件必须同时具备,缺一不可)
针对训练
·
C
O
A
B
·
C
O
B
·
C
O
B
A
A
·
C
O
A
B
·
C
O
B
·
C
O
B
A
A
下列各图中的∠BAC是否为圆周角并简述理由.
(2)
(1)
(3)
(5)
(6)
顶点不在圆上
顶点不在圆上
边AC没有和圆相交
√
√
√
新知讲解
如图,连接BO、CO,得圆心角∠BOC.试猜想∠BAC与∠BOC存在怎样的数量关系.
新知讲解
圆心O 在∠BAC 的 内部
圆心O在∠BAC的一边上
圆心O在∠BAC
的外部
新知讲解
圆心O在∠BAC的一边上(特殊情形)
OA=OC
∠A= ∠C
∠BOC= ∠ A+ ∠C
新知讲解
O
A
B
D
O
A
C
D
O
A
B
C
D
圆心O在∠BAC的内部
O
A
C
D
O
A
B
D
新知讲解
O
A
B
D
C
O
A
D
C
O
A
B
D
C
O
A
D
O
A
B
D
C
O
A
D
O
A
B
D
圆心O在∠BAC的外部
新知讲解
一条弧所对的圆周角等于该弧它所对的圆心角的一半;
圆周角定理
新知讲解
【思考】改变动点C在圆周上的位置,看看圆周角的度数有没有变化?你发现了什么?
同弧所对的圆周角的度数都相等
新知讲解
D
A
B
O
C
E
F
如图,若弧CD=弧EF, ∠A与∠B相等吗?
解:相等
思考:反过来,若∠A=∠B,那么弧CD=弧EF 成立吗?
如果把上述发现的结论中的“同弧”改为“等弧”,结论还正确吗?
∵弧CD=弧EF
新知讲解
如图,BC是⊙O的直径.请问:BC所对的圆周角∠BAC是锐角、直角还是钝角?
∵OA=OB=OC,
∴△AOC、△BOA都是等腰三角形.
∴ ∠OAC=∠OCA,∠OBA=∠OAB.
又∵ ∠OBA+∠OCA+∠CAB=180°,
∴ ∠BAC=∠OAC+∠OAB=180°÷2=90°.
解:∠BAC是直角,理由如下:
连接AO,
若圆周角∠BAC=90°,那么它所对的弦BC经过圆心吗?
新知讲解
半圆(或直径)所对的圆周角是直角,
90°的圆周角所对的弦是直径.
圆周角和直径的关系:
BC是圆O的直径
∠BAC=90°
新知讲解
例4 如图,⊙O的直径AB为10cm,弦AC为6cm. ∠ACB的平分线交⊙O于D. 求BC、AD、BD的长.
解:∵AB是直径,
∴ ∠ACB=∠ADB=90°.
在Rt△ACB中,根据勾股定理得
新知讲解
∵CD平分∠ACB,
∴∠ACD=∠DCB.
∴∠AOD=∠BOD,
∴AD=BD.
在Rt△ABD中,AD2+BD2=AB2,
新知讲解
观察下面的图形,图中的多边形与圆有什么样的位置关系?
如果一个多边形的所有顶点都在同一个圆上,这个多边形叫做圆内接多边形,这个圆叫做这个多边形的外接圆.
新知讲解
如图,四边形ABCD为⊙O的内接四边形,⊙O为四边形ABCD的外接圆.
猜想:∠A与∠C, ∠B与∠D之间的关系为:
∠A+ ∠C=180 ,
∠B+ ∠D=180
想一想:如何证明你的猜想呢?
新知讲解
证明:∵ 弧BCD和弧BAD所对的圆心角的和是周角,
∴∠A+∠C=180°,
同理∠B+∠D=180°,
推论:圆内接四边形的对角互补.
新知讲解
C
O
D
B
A
∵ 弧BCD和弧BAD所对的圆心角的和是周角,
∴∠A+∠C=180°,
同理∠B+∠D=180°,
E
延长BC到点E,有
∠BCD+∠DCE=180°.
∴∠A=∠DCE.
图中∠A与∠DCE的大小有何关系?
推论:圆的内接四边形的任何一个外角都等于它的内对角.
课堂练习
A
B
C
D
O
1.如图,四边形ABCD内接于⊙O,如果∠BOD=130°,则∠BAD的度数是( )
A 115° B 130° C 65° D 50°
A
2.如图,已知BD是⊙O的直径,⊙O的弦AC⊥BD于点E,若∠AOD=60°,则∠DBC的度数为( )
A.30° B.40° C.50° D.60°
A
课堂练习
3.如图,四边形ABCD内接于⊙O,如果∠BOD=130°,则∠BCD的度数是( )
A 115° B 130°
C 65° D 50°
4.如图,等边三角形ABC内接于⊙O,P是AC上的一点,则∠APC= .
A
B
C
D
O
A
B
C
P
C
120°
课堂练习
5.如图,四边形ABCD内接于⊙O,点E在BC的延长线上,若∠BOD=120°,则∠DCE=______°.
60
6.已知△ABC的三个顶点在⊙O上,∠BAC=60°,
∠ABC=45°, 则∠AOB= .
B
A
C
O
150°
课堂练习
7.如图,AB是⊙O的直径,AB=10 cm,∠ADE=60°,DC平∠ADE,求AC,BC的长.
解:∵∠ADE=60°,DC平分∠ADE,
∴∠ADC= ∠ADE=30°,
∴∠ABC=∠ADC=30°.
又∵AB为⊙O的直径,
∴∠ACB=90°,
∴AC= AB=5 cm.
课堂练习
8.如图,AB为⊙O的直径,CF⊥AB于E,交⊙O于D,AF交⊙O于G. 求证:∠FGD=∠ADC.
证明:∵四边形ACDG内接于⊙O,∴∠FGD=∠ACD.
又∵AB为⊙O的直径,CF⊥AB于E,∴AB垂直平分CD,
∴AC=AD,
∴∠ADC=∠ACD,
∴∠FGD=∠ADC.
课堂小结
圆心角
类比
圆周角
圆周角定义
圆周角定理
圆周角定理的推论
圆周角与直
线的关系
1.顶点在圆上,2.两边都与圆相交的角(二者必须同时具备)
半圆或直径所对的圆周角都相等,都等于90°(直角).
在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于该弧所对的圆心角的一半;相等的圆周角所对的弧相等.
1.90°的圆周角所对的弦是直径;
2.圆内接四边形的对角互补.
圆周角
课堂小结
如果一个多边形所有顶点都在同一个圆上,这个多边形叫做圆内接多边形,这个圆叫做这个多边形的外接圆.
圆内接多边形
性质2:圆的内接四边形的任何一个外角都等于它的内对角.
性质1:圆的内接四边形的对角互补.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
