平行线[下学期]
图片预览
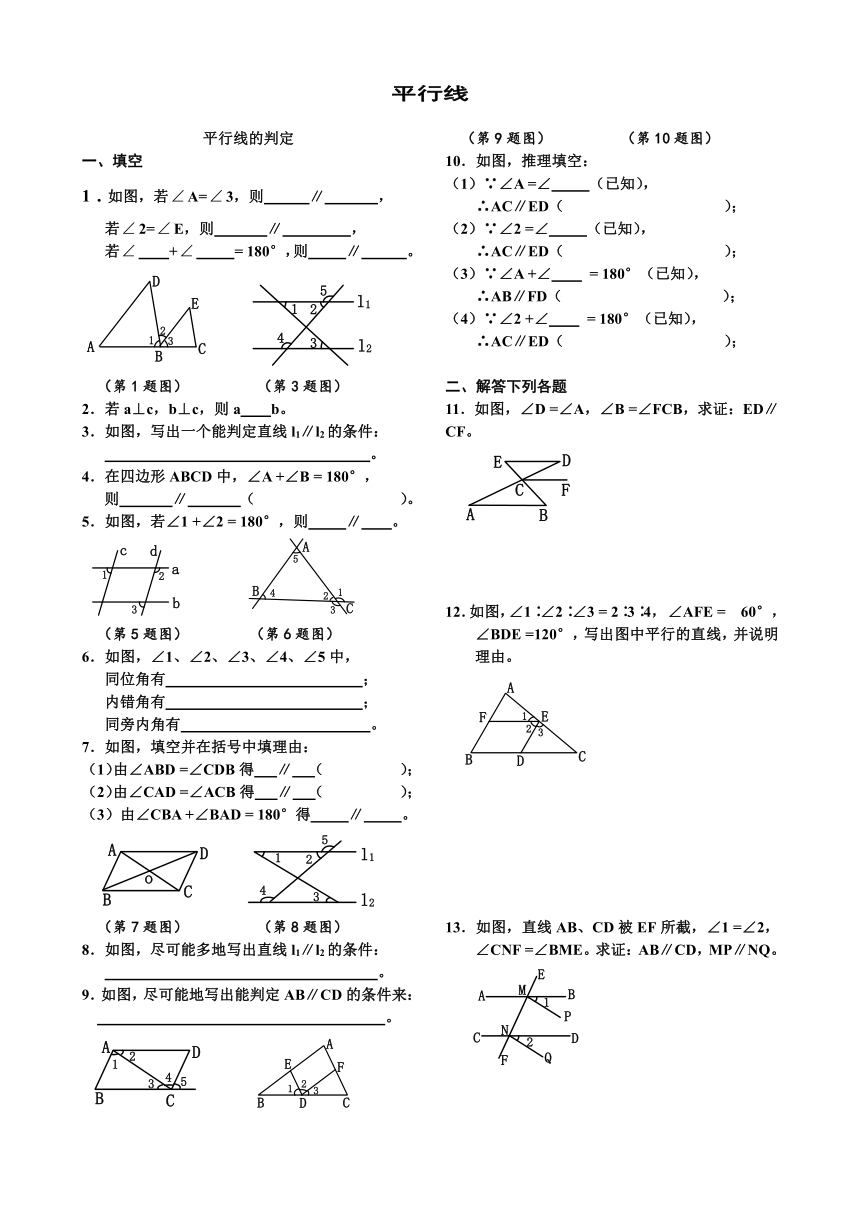
文档简介
平行线
平行线的判定
一、填空
1.如图,若A=3,则 ∥ ,
若2=E,则 ∥ ,
若 + = 180°,则 ∥ 。
(第1题图) (第3题图)
2.若a⊥c,b⊥c,则a b。
3.如图,写出一个能判定直线l1∥l 2的条件:
。
4.在四边形ABCD中,∠A +∠B = 180°,
则 ∥ ( )。
5.如图,若∠1 +∠2 = 180°,则 ∥ 。
(第5题图) (第6题图)
6.如图,∠1、∠2、∠3、∠4、∠5中,
同位角有 ;
内错角有 ;
同旁内角有 。
7.如图,填空并在括号中填理由:
(1)由∠ABD =∠CDB得 ∥ ( );
(2)由∠CAD =∠ACB得 ∥ ( );
(3)由∠CBA +∠BAD = 180°得 ∥ 。
(第7题图) (第8题图)
8.如图,尽可能多地写出直线l1∥l 2的条件:
。
9.如图,尽可能地写出能判定AB∥CD的条件来:
。
(第9题图) (第10题图)
10.如图,推理填空:
(1)∵∠A =∠ (已知),
∴AC∥ED( );
(2)∵∠2 =∠ (已知),
∴AC∥ED( );
(3)∵∠A +∠ = 180°(已知),
∴AB∥FD( );
(4)∵∠2 +∠ = 180°(已知),
∴AC∥ED( );
二、解答下列各题
11.如图,∠D =∠A,∠B =∠FCB,求证:ED∥CF。
12.如图,∠1∶∠2∶∠3 = 2∶3∶4, ∠AFE = 60°,∠BDE =120°,写出图中平行的直线,并说明理由。
13.如图,直线AB、CD被EF所截,∠1 =∠2,∠CNF =∠BME。求证:AB∥CD,MP∥NQ。
平行线的性质
一、填空
1.如图,已知∠1 = 100°,AB∥CD,则∠2 = ,∠3 = ,∠4 = 。
(第1题图) (第2题图)
2.如图,直线AB、CD被EF所截,若∠1 =∠2,则∠AEF +∠CFE = 。
3.如图所示
(1)若EF∥AC,则∠A +∠ = 180°,∠F + ∠ = 180°( )。
(2)若∠2 =∠ ,则AE∥BF。
(3)若∠A +∠ = 180°,则AE∥BF。
(第3题图) (第4题图)
4.如图,AB∥CD,∠2 = 2∠1,则∠2 = 。
5.如图,AB∥CD,EG⊥AB于G,∠1 = 50°,则∠E = 。
(第5题图) (第6题图)
6.如图,直线l1∥l2,AB⊥l1于O,BC与l2交于E,∠1 = 43°,则∠2 = 。
7.如图,AB∥CD,AC⊥BC,图中与∠CAB互余的角有 。
(第7题图) (第8题图)
8.如图,AB∥EF∥CD,EG∥BD,则图中与∠1相等的角(不包括∠1)共有 个。
二、解答下列各题
9.如图,已知∠ABE +∠DEB = 180°,∠1 =∠2,求证:∠F =∠G。
10.如图,DE∥BC,∠D∶∠DBC = 2∶1,∠1 =∠2,求∠DEB的度数。
11.如图,已知AB∥CD,试再添上一个条件,使∠1 =∠2成立。(要求给出两个以上答案,并选择其中一个加以证明)
12.如图,∠ABD和∠BDC的平分线交于E,BE交CD于点F,∠1 +∠2 = 90°。求证:
(1)AB∥CD; (2)∠2 +∠3 = 90°。
参考答案
平行线的判定
1.AD,BE;BD,EC;AD,BE。
2.∥
3.∠4 =∠5,∠1 =∠3,∠4 +∠2 =180°。
4.AD∥BC(同旁内角互补,两直线平行)
5.c∥d
6.∠1与∠4,∠3与∠5;∠3与∠4,∠1与∠5;∠2与∠4,∠2与∠5,∠4与∠5。
7.(1)AB∥CD(内错角相等,两直线平行)
(2)AD∥BC(内错角相等,两直线平行)
(3)AD∥BC。
8.∠4 =∠5,∠1 =∠3,∠2 +∠4 =180°
9.∠B =∠5,∠1 =∠4,∠B +∠BCD = 180°,∠D +∠BAD = 180°
10.(1)BED,同位角相等,两直线平行;
(2)DFC,内错角相等,两直线平行;
(3)AFD,同旁内角互补,两直线平行;
(4)AFD,同旁内角互补,两直线平行。
11.略
12.略
13.略
平行线的性质
1.100°,100°,80°
2.180°
3.(1)AEF,ABF,两直线平行,同旁内角互补。
(2)4
(3)ABF
4.120°
5.40°
6.133°
7.∠ABC,∠BCD,∠EBF。
8.5个
9.略
10.30°
11.补充的条件可以是 :
①AE、PF分别平分∠BAP、∠APC;
②AE∥PF;
③∠E =∠F;
④∠EAP =∠APF;等。
证明略。
12.略。
平行线的判定
一、填空
1.如图,若A=3,则 ∥ ,
若2=E,则 ∥ ,
若 + = 180°,则 ∥ 。
(第1题图) (第3题图)
2.若a⊥c,b⊥c,则a b。
3.如图,写出一个能判定直线l1∥l 2的条件:
。
4.在四边形ABCD中,∠A +∠B = 180°,
则 ∥ ( )。
5.如图,若∠1 +∠2 = 180°,则 ∥ 。
(第5题图) (第6题图)
6.如图,∠1、∠2、∠3、∠4、∠5中,
同位角有 ;
内错角有 ;
同旁内角有 。
7.如图,填空并在括号中填理由:
(1)由∠ABD =∠CDB得 ∥ ( );
(2)由∠CAD =∠ACB得 ∥ ( );
(3)由∠CBA +∠BAD = 180°得 ∥ 。
(第7题图) (第8题图)
8.如图,尽可能多地写出直线l1∥l 2的条件:
。
9.如图,尽可能地写出能判定AB∥CD的条件来:
。
(第9题图) (第10题图)
10.如图,推理填空:
(1)∵∠A =∠ (已知),
∴AC∥ED( );
(2)∵∠2 =∠ (已知),
∴AC∥ED( );
(3)∵∠A +∠ = 180°(已知),
∴AB∥FD( );
(4)∵∠2 +∠ = 180°(已知),
∴AC∥ED( );
二、解答下列各题
11.如图,∠D =∠A,∠B =∠FCB,求证:ED∥CF。
12.如图,∠1∶∠2∶∠3 = 2∶3∶4, ∠AFE = 60°,∠BDE =120°,写出图中平行的直线,并说明理由。
13.如图,直线AB、CD被EF所截,∠1 =∠2,∠CNF =∠BME。求证:AB∥CD,MP∥NQ。
平行线的性质
一、填空
1.如图,已知∠1 = 100°,AB∥CD,则∠2 = ,∠3 = ,∠4 = 。
(第1题图) (第2题图)
2.如图,直线AB、CD被EF所截,若∠1 =∠2,则∠AEF +∠CFE = 。
3.如图所示
(1)若EF∥AC,则∠A +∠ = 180°,∠F + ∠ = 180°( )。
(2)若∠2 =∠ ,则AE∥BF。
(3)若∠A +∠ = 180°,则AE∥BF。
(第3题图) (第4题图)
4.如图,AB∥CD,∠2 = 2∠1,则∠2 = 。
5.如图,AB∥CD,EG⊥AB于G,∠1 = 50°,则∠E = 。
(第5题图) (第6题图)
6.如图,直线l1∥l2,AB⊥l1于O,BC与l2交于E,∠1 = 43°,则∠2 = 。
7.如图,AB∥CD,AC⊥BC,图中与∠CAB互余的角有 。
(第7题图) (第8题图)
8.如图,AB∥EF∥CD,EG∥BD,则图中与∠1相等的角(不包括∠1)共有 个。
二、解答下列各题
9.如图,已知∠ABE +∠DEB = 180°,∠1 =∠2,求证:∠F =∠G。
10.如图,DE∥BC,∠D∶∠DBC = 2∶1,∠1 =∠2,求∠DEB的度数。
11.如图,已知AB∥CD,试再添上一个条件,使∠1 =∠2成立。(要求给出两个以上答案,并选择其中一个加以证明)
12.如图,∠ABD和∠BDC的平分线交于E,BE交CD于点F,∠1 +∠2 = 90°。求证:
(1)AB∥CD; (2)∠2 +∠3 = 90°。
参考答案
平行线的判定
1.AD,BE;BD,EC;AD,BE。
2.∥
3.∠4 =∠5,∠1 =∠3,∠4 +∠2 =180°。
4.AD∥BC(同旁内角互补,两直线平行)
5.c∥d
6.∠1与∠4,∠3与∠5;∠3与∠4,∠1与∠5;∠2与∠4,∠2与∠5,∠4与∠5。
7.(1)AB∥CD(内错角相等,两直线平行)
(2)AD∥BC(内错角相等,两直线平行)
(3)AD∥BC。
8.∠4 =∠5,∠1 =∠3,∠2 +∠4 =180°
9.∠B =∠5,∠1 =∠4,∠B +∠BCD = 180°,∠D +∠BAD = 180°
10.(1)BED,同位角相等,两直线平行;
(2)DFC,内错角相等,两直线平行;
(3)AFD,同旁内角互补,两直线平行;
(4)AFD,同旁内角互补,两直线平行。
11.略
12.略
13.略
平行线的性质
1.100°,100°,80°
2.180°
3.(1)AEF,ABF,两直线平行,同旁内角互补。
(2)4
(3)ABF
4.120°
5.40°
6.133°
7.∠ABC,∠BCD,∠EBF。
8.5个
9.略
10.30°
11.补充的条件可以是 :
①AE、PF分别平分∠BAP、∠APC;
②AE∥PF;
③∠E =∠F;
④∠EAP =∠APF;等。
证明略。
12.略。
