如皋初级中学七下课件平行线性质[1][下学期]
文档属性
| 名称 | 如皋初级中学七下课件平行线性质[1][下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 232.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-02-25 00:00:00 | ||
图片预览


文档简介
课件18张PPT。复习回顾新课学习巩固练习课堂小结 平行线的判定方法有哪三种?它
们是先知道什么……、 后知道什么? 同位角相等
内错角相等
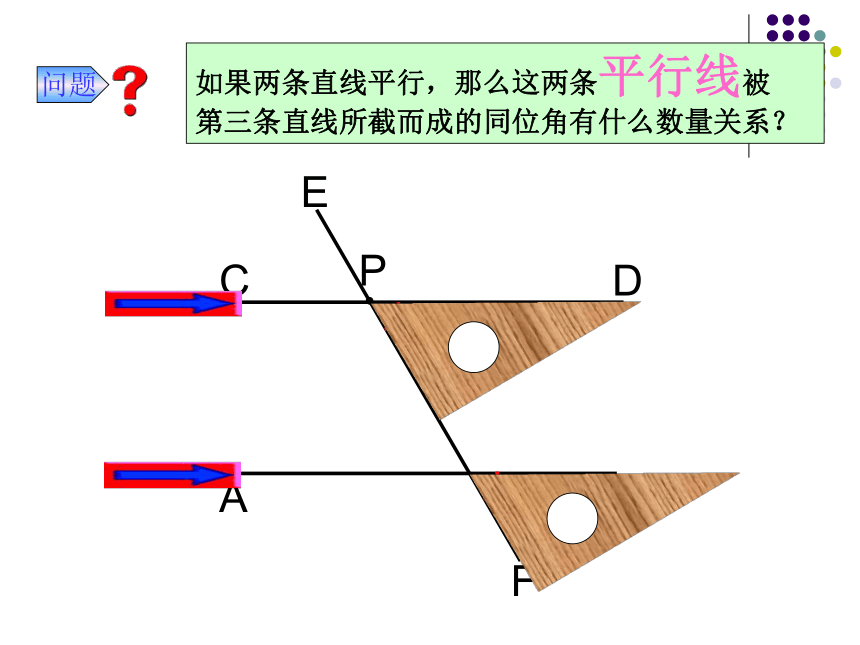
同旁内角互补两直线平行问题如果两条直线平行,那么这两条平行线被
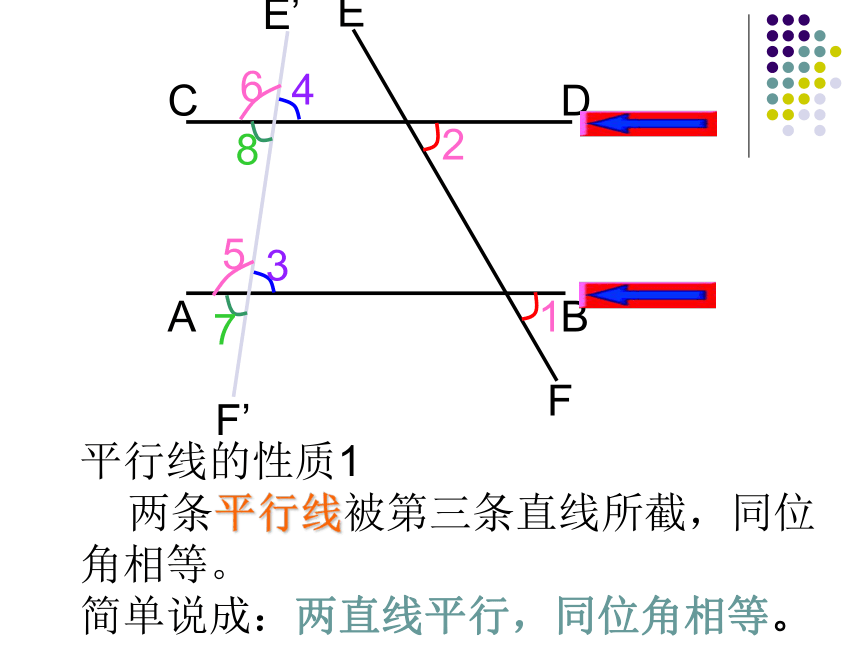
第三条直线所截而成的同位角有什么数量关系?问题平行线的性质1
两条平行线被第三条直线所截,同位
角相等。
简单说成:两直线平行,同位角相等。
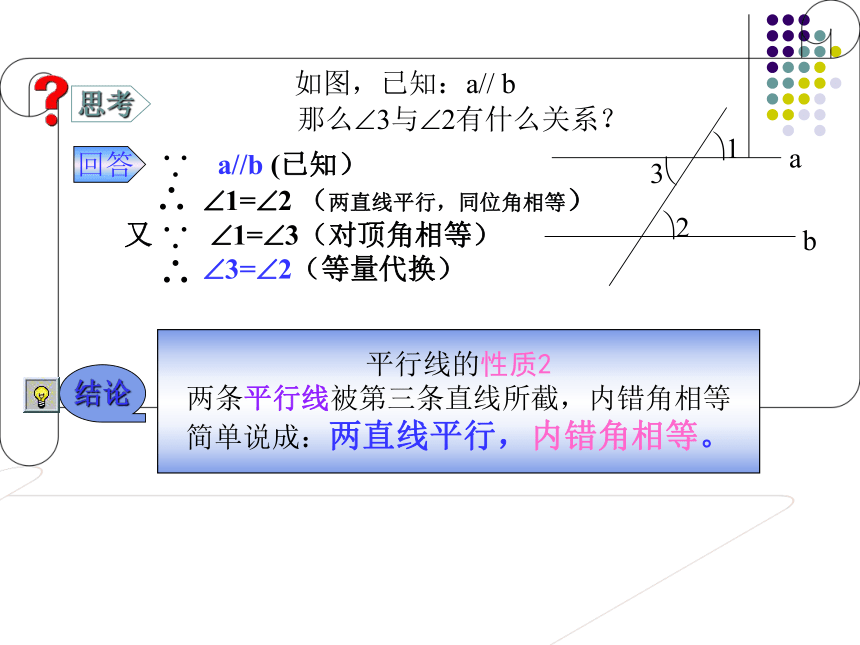
a//b (已知)
?1=?2 (两直线平行,同位角相等)
又 ?1=?3(对顶角相等)
?3=?2(等量代换)
思考回答????如图,已知:a// b
那么?3与?2有什么关系? 平行线的性质2
两条平行线被第三条直线所截,内错角相等
简单说成:两直线平行,内错角相等。结论c
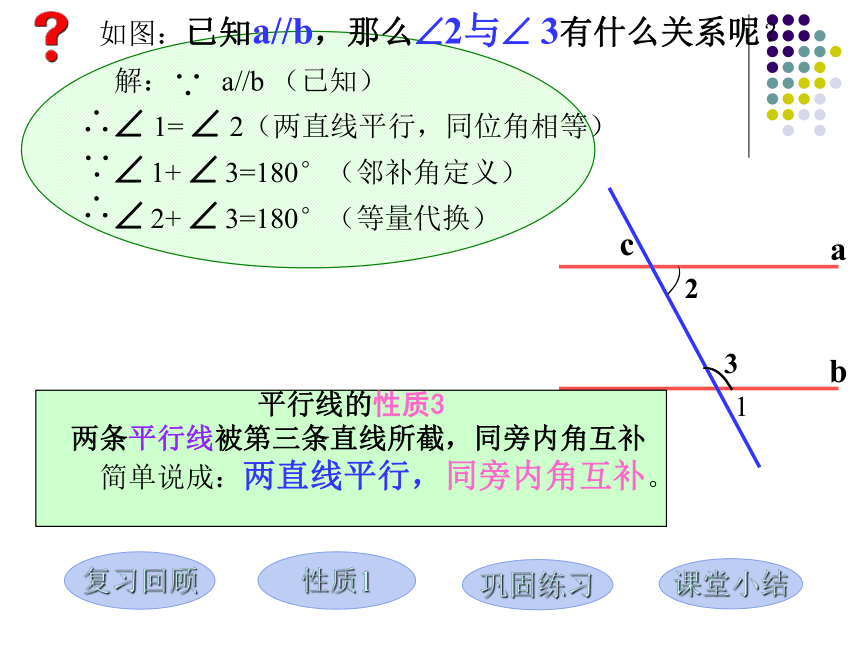
解: a//b (已知)
? 1= ? 2(两直线平行,同位角相等)
? 1+ ? 3=180°(邻补角定义)
? 2+ ? 3=180°(等量代换)
如图:已知a//b,那么?2与? 3有什么关系呢?平行线的性质3
两条平行线被第三条直线所截,同旁内角互补
简单说成:两直线平行,同旁内角互补。
???复习回顾性质1巩固练习课堂小结?平行线的性质1(公理)
两条平行线被第三条直线所截,同位角相等。
简单说成:两直线平行,同位角相等。平行线的性质2
两条平行线被第三条直线所截,内错角相等
简单说成:两直线平行,内错角相等。平行线的性质3
两条平行线被第三条直线所截,同旁内角互补
简单说成:两直线平行,同旁内角互补。
精彩回放复习回顾新课学习巩固练习课堂小结如图: ?1= ? 2(已知)
AD// BC
( )
? BCD+ ? D=180?
( )BC内错角相等,两直线平行两直线平行,同旁内角互补???例1:填空复习回顾新课学习巩固练习课堂小结例2 如图所示 ∠1 =∠2
说明 : ∠3 =∠4说明:∵ ∠1 =∠2(已知) ∴a//b
(同位角相等,两直线平行) ∴ ∠3 =∠4
(两直线平行,内错角相等)说明:因为? AD∥BC,( )所以? ∠A+∠AEF=180°,因为? ∠AEF=∠B,所以? ∠A+∠B=180°.所以? AD∥EF.已知( )( )( )( )两直线平行,同旁内角互补已知等量代换同旁内角互补,两直线平行例3? 如图所示.
已知:AD∥BC,
∠AEF=∠B,
说明:AD∥EF. 已知角之间的关系(相等或互补),得到两直线平行
的结论是平行线的判定。
已知两直线平行,得到角之间的关系(相等或互补)
的结论是平行线的性质。练习1 如图,已知直线a∥b,
∠3=131°,求∠ 1、∠2的度数。解(1)∵∠1=∠3 (对顶角相等)
且∠3=131°(已知)
∴∠1 =131°(2)∵a∥b(已知)
∴∠1+∠2=180°(两直线平行,
同旁内角互补)
又 ∵ ∠1=131°
∴ ∠2=49°。解:∵AD//BC (已知)
∴? A + ? B=180°
(两直线平行,同旁内角互补)
∴? B= 180 °- ? A =180 ° -115 °=65 °
∵AD//BC (已知)
∴? D+ ? C=180 °
(两直线平行,同旁内角互补)
即? C=180 °- ? D =180 ° -100 ° =80 °
答:梯形的另外两个角分别为65 ° 、80 ° 。复习回顾新课学习巩固练习课堂小结练习3:如图,已知AG//CF,AB//CD,∠A=40?,求∠C的度数。1解:∵ AG//CF(已知)∴ ∠A=∠1(两直线平行,同位角相等)又∵AB//CD(已知)∴ ∠1=∠C(两直线平行,同位角相等)∴ ∠A=∠C(等量代换)∵ ∠A=40?∴ ∠C=40?练习4,如图:一束平行光线AB和DE射向一个水平镜面后被发射,此时∠1=∠2 , ∠3=∠4 。(1 )∠1、∠3的大小有什么关系?∠2与∠4呢?∵AB∥DE ∴∠1=∠3相等你知道理由吗?两直线平行
同位角相等(2 )发射光线BC与EF也平行吗?∵ ∠2=∠4 ∴ BC∥EF 平行同位角相等
两直线平行∵ ∠1=∠3 且 ∠1=∠2 ,∠3=∠4∴ ∠2=∠4 同位角相等
内错角相等
同旁内角互补两直线平行判定性质小结:复习回顾新课学习巩固练习课堂小结(1)∵AB∥CD(已知)∴∠1=∠2(两直线平行,内错角相等)又∵∠1=110°∴∠1=∠2=110°(已知)(等量代换)(2)∵AB∥CD(已知)∴∠1=∠3(两直线平行,同位角相等)又∵∠1=110°∴∠1=∠3=110°(已知)(等量代换)(3)∵AB∥CD(已知)∴∠1+∠4=180°(两直线平行,内错角相等)又∵∠1=110°(已知)∴110 ° +∠4=180°(等量代换)∴∠4=180°-110°=70°(等式性质)解答:P.25EX.3复习回顾新课学习巩固练习课堂小结再见
们是先知道什么……、 后知道什么? 同位角相等
内错角相等
同旁内角互补两直线平行问题如果两条直线平行,那么这两条平行线被
第三条直线所截而成的同位角有什么数量关系?问题平行线的性质1
两条平行线被第三条直线所截,同位
角相等。
简单说成:两直线平行,同位角相等。
a//b (已知)
?1=?2 (两直线平行,同位角相等)
又 ?1=?3(对顶角相等)
?3=?2(等量代换)
思考回答????如图,已知:a// b
那么?3与?2有什么关系? 平行线的性质2
两条平行线被第三条直线所截,内错角相等
简单说成:两直线平行,内错角相等。结论c
解: a//b (已知)
? 1= ? 2(两直线平行,同位角相等)
? 1+ ? 3=180°(邻补角定义)
? 2+ ? 3=180°(等量代换)
如图:已知a//b,那么?2与? 3有什么关系呢?平行线的性质3
两条平行线被第三条直线所截,同旁内角互补
简单说成:两直线平行,同旁内角互补。
???复习回顾性质1巩固练习课堂小结?平行线的性质1(公理)
两条平行线被第三条直线所截,同位角相等。
简单说成:两直线平行,同位角相等。平行线的性质2
两条平行线被第三条直线所截,内错角相等
简单说成:两直线平行,内错角相等。平行线的性质3
两条平行线被第三条直线所截,同旁内角互补
简单说成:两直线平行,同旁内角互补。
精彩回放复习回顾新课学习巩固练习课堂小结如图: ?1= ? 2(已知)
AD// BC
( )
? BCD+ ? D=180?
( )BC内错角相等,两直线平行两直线平行,同旁内角互补???例1:填空复习回顾新课学习巩固练习课堂小结例2 如图所示 ∠1 =∠2
说明 : ∠3 =∠4说明:∵ ∠1 =∠2(已知) ∴a//b
(同位角相等,两直线平行) ∴ ∠3 =∠4
(两直线平行,内错角相等)说明:因为? AD∥BC,( )所以? ∠A+∠AEF=180°,因为? ∠AEF=∠B,所以? ∠A+∠B=180°.所以? AD∥EF.已知( )( )( )( )两直线平行,同旁内角互补已知等量代换同旁内角互补,两直线平行例3? 如图所示.
已知:AD∥BC,
∠AEF=∠B,
说明:AD∥EF. 已知角之间的关系(相等或互补),得到两直线平行
的结论是平行线的判定。
已知两直线平行,得到角之间的关系(相等或互补)
的结论是平行线的性质。练习1 如图,已知直线a∥b,
∠3=131°,求∠ 1、∠2的度数。解(1)∵∠1=∠3 (对顶角相等)
且∠3=131°(已知)
∴∠1 =131°(2)∵a∥b(已知)
∴∠1+∠2=180°(两直线平行,
同旁内角互补)
又 ∵ ∠1=131°
∴ ∠2=49°。解:∵AD//BC (已知)
∴? A + ? B=180°
(两直线平行,同旁内角互补)
∴? B= 180 °- ? A =180 ° -115 °=65 °
∵AD//BC (已知)
∴? D+ ? C=180 °
(两直线平行,同旁内角互补)
即? C=180 °- ? D =180 ° -100 ° =80 °
答:梯形的另外两个角分别为65 ° 、80 ° 。复习回顾新课学习巩固练习课堂小结练习3:如图,已知AG//CF,AB//CD,∠A=40?,求∠C的度数。1解:∵ AG//CF(已知)∴ ∠A=∠1(两直线平行,同位角相等)又∵AB//CD(已知)∴ ∠1=∠C(两直线平行,同位角相等)∴ ∠A=∠C(等量代换)∵ ∠A=40?∴ ∠C=40?练习4,如图:一束平行光线AB和DE射向一个水平镜面后被发射,此时∠1=∠2 , ∠3=∠4 。(1 )∠1、∠3的大小有什么关系?∠2与∠4呢?∵AB∥DE ∴∠1=∠3相等你知道理由吗?两直线平行
同位角相等(2 )发射光线BC与EF也平行吗?∵ ∠2=∠4 ∴ BC∥EF 平行同位角相等
两直线平行∵ ∠1=∠3 且 ∠1=∠2 ,∠3=∠4∴ ∠2=∠4 同位角相等
内错角相等
同旁内角互补两直线平行判定性质小结:复习回顾新课学习巩固练习课堂小结(1)∵AB∥CD(已知)∴∠1=∠2(两直线平行,内错角相等)又∵∠1=110°∴∠1=∠2=110°(已知)(等量代换)(2)∵AB∥CD(已知)∴∠1=∠3(两直线平行,同位角相等)又∵∠1=110°∴∠1=∠3=110°(已知)(等量代换)(3)∵AB∥CD(已知)∴∠1+∠4=180°(两直线平行,内错角相等)又∵∠1=110°(已知)∴110 ° +∠4=180°(等量代换)∴∠4=180°-110°=70°(等式性质)解答:P.25EX.3复习回顾新课学习巩固练习课堂小结再见
