平行线性质的复习[下学期]
文档属性
| 名称 | 平行线性质的复习[下学期] |  | |
| 格式 | rar | ||
| 文件大小 | 134.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-02-27 23:08:00 | ||
图片预览



文档简介
课件15张PPT。 平行线的性质复习路桥二中数学组温故知新1.平行线的判定方法有哪些?2.平行线有哪些性质?3.你会区别平行线的判定和性质吗?
根据右边的图形,在括号内填上相应的理由:
①∵∠1=∠C( )
∴AB∥CD(
② ∵∠1=∠B( )
∴EC∥BD(
③ ∵∠2+∠B=180°( )
∴EC∥BD(
④ ∵AB∥CD( )
∴ ∠3=∠C( )
⑤ ∵EC∥BD( )
∴ ∠3=∠B( )
⑥ ∵AB∥CD( )
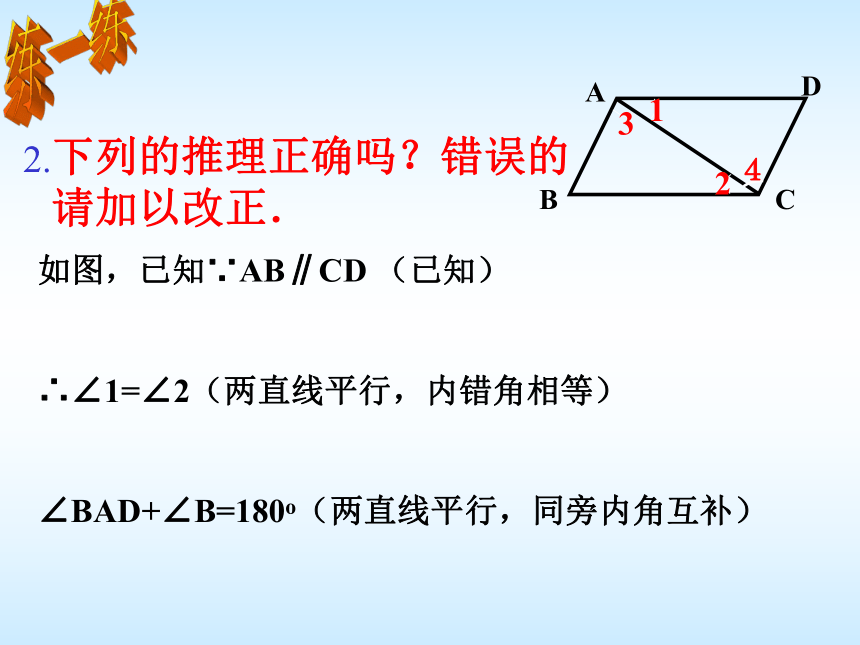
∴ ∠2+∠C= 180° ( )练一练1.已知两直线平行,同位角相等已知内错角相等,两直线平行已知同旁内角互补,两直线平行已知两直线平行,内错角相等已知已知两直线平行,同旁内角互补同位角相等,两直线平行如图,已知∵AB∥CD (已知)
∴∠1=∠2(两直线平行,内错角相等)
∠BAD+∠B=180o(两直线平行,同旁内角互补)ABCD321练一练下列的推理正确吗?错误的
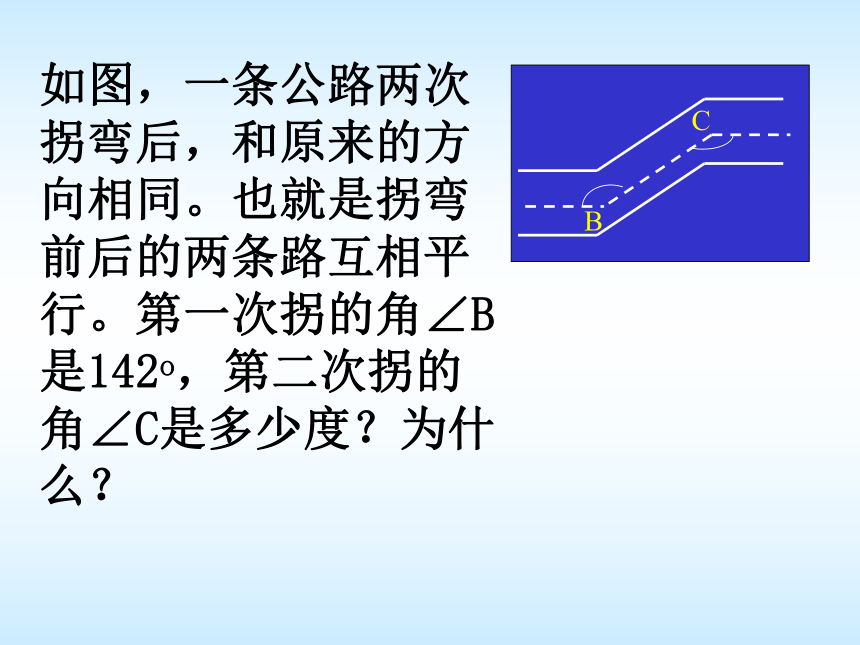
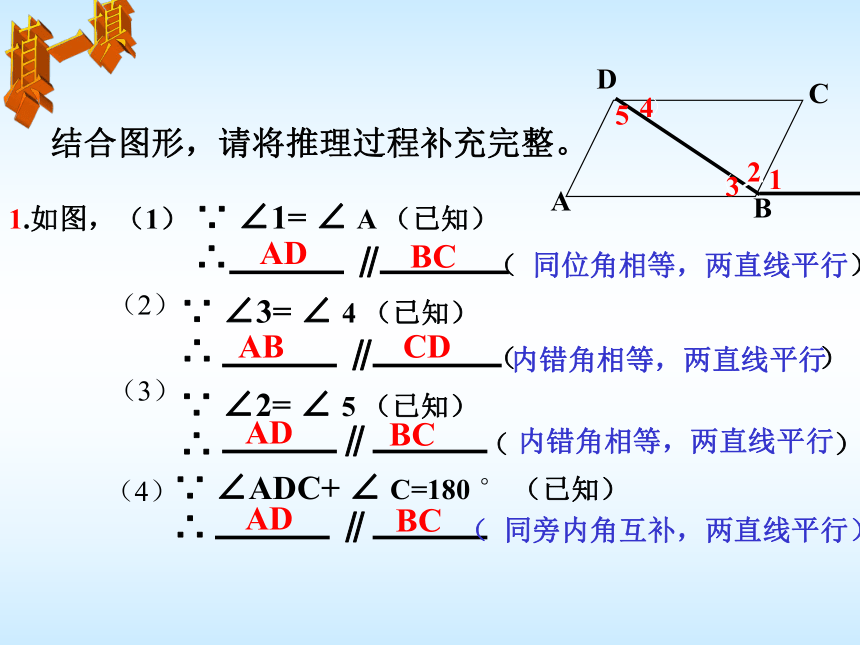
请加以改正.2.4如图,一条公路两次拐弯后,和原来的方向相同。也就是拐弯前后的两条路互相平行。第一次拐的角∠B是142o,第二次拐的角∠C是多少度?为什么?填一填结合图形,请将推理过程补充完整。1.如图,(1) ∵ ∠1= ∠ A (已知)
∴ABCD32145∥( 同位角相等,两直线平行) )(2)∵ ∠3= ∠ 4 (已知)
∴∥( )(3)∵ ∠2= ∠ 5 (已知)
∴∥( )(4)∵ ∠ADC+ ∠ C=180 ° (已知)
∴∥( 同旁内角互补,两直线平行) )ADBCABCDADBCADBC内错角相等,两直线平行 )
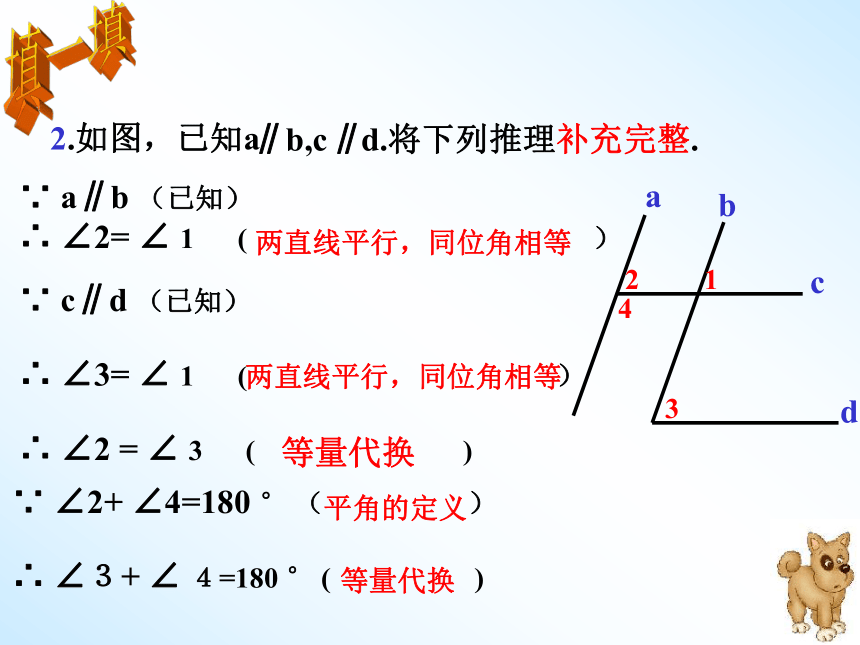
内错角相等,两直线平行填一填2.如图,已知a ∥∥b,c d.将下列推理补充完整.1234abcd∵ a∥b (已知)
∴ ∠2= ∠ 1 ( )∵ c∥d (已知)
∴ ∠3= ∠ 1 ( )
∴ ∠2 = ∠ 3 ( ) ∵ ∠2+ ∠4=180 ° ( )
∴ ∠3+ ∠ 4=180 ° ( )
等量代换两直线平行,同位角相等平角的定义等量代换两直线平行,同位角相等
填一填3.如图,E在直线DF上,B在直线AC上,若∠AGB
= ∠EHF,∠C= ∠D,则∠A= ∠F.下面是它的推理过程,
请结合图形将它补充完整.ABCDEFGH解: ∵ ∠AGB= ∠EHF( )
∠AGB= ∠DGF( )
∴ ∠EHF = ∠DGF( )
∴DB CE ( )
∴ ∠D= ∠FEC ( )
∵ ∠C= ∠D ( )
∴ ∠FEC = ∠C ( )
∴ DF ∥AC ( )
∴ ∠A= ∠F ( )
∥已知对顶角相等等量代换同位角相等,两直线平行已知等量代换内错角相等,两直线平行两直线平行,内错角相等两直线平行,同位角相等试一试如图,已知AB ∥ CD, ∠1=∠2,那么∠E与∠F相等吗?试作出判断并说出你的理由。1234AB CDEF探索与思考已知,如右图
(1)若AB ∥ CD,则∠BED= ∠B+ ∠D,试说明理由.
(2)若∠BED= ∠B+ ∠D, 那么AB ∥ CD吗?请写出你的推理过程。
AB CDE小结:本节课你有何收获?作业:1.作业本
2.习题5.3第7至12题.
3.同步练习ABCD2.(1)当______∥______时,∠ABD=∠CDB;
(2)当_______∥_______时,∠ADB=∠ CBD;
(3)当_______∥_______时,∠BAC=∠DCA;
(4)当_______+_______=180°时,AD∥BC
(5)当_______∥_______时,∠BAD+∠ADC=180°1.当AB∥CD时,则下列结论成立的是( )
∠DAC=∠ACB (B) ∠DAB+∠ABC=180°(C)∠ADB=∠DBC (D) ∠BAC=∠ACD DABCDADBCABCD∠DAB∠ABCABCD补充练习3.A岛观察B岛,在北偏西35°方向,那么B岛观察A岛的方向是( )
(A)南偏西55° (B)南偏西35°
(C)南偏东35° (D)南偏东55°4.宁波到台州的高速公路需开挖山洞,为节约
开挖时间,需在山的两面A、B同时开工,
在A处测得洞的走向是北偏东75°,那么在
B处应按_________方向开工,才能使此洞两
边准确接通.5.已知:如图∠1= ∠ 2, ∠ A= ∠ C, 说明:AE∥BCADCBE123再 见 !!
根据右边的图形,在括号内填上相应的理由:
①∵∠1=∠C( )
∴AB∥CD(
② ∵∠1=∠B( )
∴EC∥BD(
③ ∵∠2+∠B=180°( )
∴EC∥BD(
④ ∵AB∥CD( )
∴ ∠3=∠C( )
⑤ ∵EC∥BD( )
∴ ∠3=∠B( )
⑥ ∵AB∥CD( )
∴ ∠2+∠C= 180° ( )练一练1.已知两直线平行,同位角相等已知内错角相等,两直线平行已知同旁内角互补,两直线平行已知两直线平行,内错角相等已知已知两直线平行,同旁内角互补同位角相等,两直线平行如图,已知∵AB∥CD (已知)
∴∠1=∠2(两直线平行,内错角相等)
∠BAD+∠B=180o(两直线平行,同旁内角互补)ABCD321练一练下列的推理正确吗?错误的
请加以改正.2.4如图,一条公路两次拐弯后,和原来的方向相同。也就是拐弯前后的两条路互相平行。第一次拐的角∠B是142o,第二次拐的角∠C是多少度?为什么?填一填结合图形,请将推理过程补充完整。1.如图,(1) ∵ ∠1= ∠ A (已知)
∴ABCD32145∥( 同位角相等,两直线平行) )(2)∵ ∠3= ∠ 4 (已知)
∴∥( )(3)∵ ∠2= ∠ 5 (已知)
∴∥( )(4)∵ ∠ADC+ ∠ C=180 ° (已知)
∴∥( 同旁内角互补,两直线平行) )ADBCABCDADBCADBC内错角相等,两直线平行 )
内错角相等,两直线平行填一填2.如图,已知a ∥∥b,c d.将下列推理补充完整.1234abcd∵ a∥b (已知)
∴ ∠2= ∠ 1 ( )∵ c∥d (已知)
∴ ∠3= ∠ 1 ( )
∴ ∠2 = ∠ 3 ( ) ∵ ∠2+ ∠4=180 ° ( )
∴ ∠3+ ∠ 4=180 ° ( )
等量代换两直线平行,同位角相等平角的定义等量代换两直线平行,同位角相等
填一填3.如图,E在直线DF上,B在直线AC上,若∠AGB
= ∠EHF,∠C= ∠D,则∠A= ∠F.下面是它的推理过程,
请结合图形将它补充完整.ABCDEFGH解: ∵ ∠AGB= ∠EHF( )
∠AGB= ∠DGF( )
∴ ∠EHF = ∠DGF( )
∴DB CE ( )
∴ ∠D= ∠FEC ( )
∵ ∠C= ∠D ( )
∴ ∠FEC = ∠C ( )
∴ DF ∥AC ( )
∴ ∠A= ∠F ( )
∥已知对顶角相等等量代换同位角相等,两直线平行已知等量代换内错角相等,两直线平行两直线平行,内错角相等两直线平行,同位角相等试一试如图,已知AB ∥ CD, ∠1=∠2,那么∠E与∠F相等吗?试作出判断并说出你的理由。1234AB CDEF探索与思考已知,如右图
(1)若AB ∥ CD,则∠BED= ∠B+ ∠D,试说明理由.
(2)若∠BED= ∠B+ ∠D, 那么AB ∥ CD吗?请写出你的推理过程。
AB CDE小结:本节课你有何收获?作业:1.作业本
2.习题5.3第7至12题.
3.同步练习ABCD2.(1)当______∥______时,∠ABD=∠CDB;
(2)当_______∥_______时,∠ADB=∠ CBD;
(3)当_______∥_______时,∠BAC=∠DCA;
(4)当_______+_______=180°时,AD∥BC
(5)当_______∥_______时,∠BAD+∠ADC=180°1.当AB∥CD时,则下列结论成立的是( )
∠DAC=∠ACB (B) ∠DAB+∠ABC=180°(C)∠ADB=∠DBC (D) ∠BAC=∠ACD DABCDADBCABCD∠DAB∠ABCABCD补充练习3.A岛观察B岛,在北偏西35°方向,那么B岛观察A岛的方向是( )
(A)南偏西55° (B)南偏西35°
(C)南偏东35° (D)南偏东55°4.宁波到台州的高速公路需开挖山洞,为节约
开挖时间,需在山的两面A、B同时开工,
在A处测得洞的走向是北偏东75°,那么在
B处应按_________方向开工,才能使此洞两
边准确接通.5.已知:如图∠1= ∠ 2, ∠ A= ∠ C, 说明:AE∥BCADCBE123再 见 !!
