人教版九年级数学下册 27.2.1相似三角形的判定(4) 课件(共32张PPT)
文档属性
| 名称 | 人教版九年级数学下册 27.2.1相似三角形的判定(4) 课件(共32张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-09 19:46:44 | ||
图片预览








文档简介
(共32张PPT)
相似三角形的判定(4)
一、学习目标:
1.理解三角形相似的判定定理——“两角分别相等的两个三角形相似”;
2.理解判定直角三角形相似的特殊方法——“斜边和一条直角边成比例的两个直角三角形相似”;
3.会运用三角形相似的判定定理解决简单问题.
二、学习重点:
掌握运用三角形相似的判定定理解决简单问题.
一、复习引入:
通过定义 :三个角分别相等,三条边成比例的两个三角形相似.
回忆:目前我们知道哪些判定两个三角形相似的方法
一、复习引入:
判定(1):平行于三角形一边的直线和其他两边(或延长线)相交,所构成的三角形与原三角形相似.
回忆:目前我们知道哪些判定两个三角形相似的方法
一、复习引入:
回忆:目前我们知道哪些判定两个三角形相似的方法
∵
判定(2):三边成比例的两个三角形相似.
一、复习引入:
回忆:目前我们知道哪些判定两个三角形相似的方法
∵
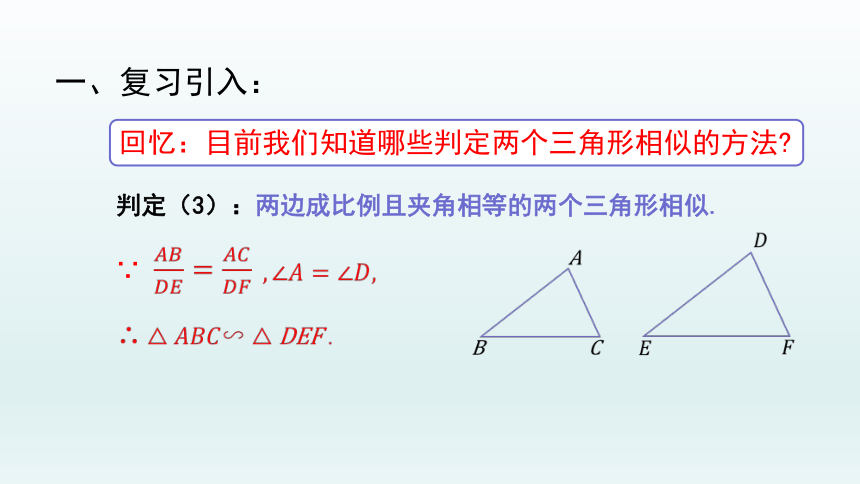
判定(3):两边成比例且夹角相等的两个三角形相似.
回忆:目前我们知道哪些判定两个三角形相似的方法
一、复习引入:
判定(1):平行于三角形一边的直线和其他两边(或延长线)相交,
所构成的三角形与原三角形相似.
判定(2):三边成比例的两个三角形相似.
判定(3):两边成比例且夹角相等的两个三角形相似.
通过定义 :三个角分别相等,三条边成比例的两个三角形相似.
判定两个三角形相似还有其他方法吗
二、新知探究一:
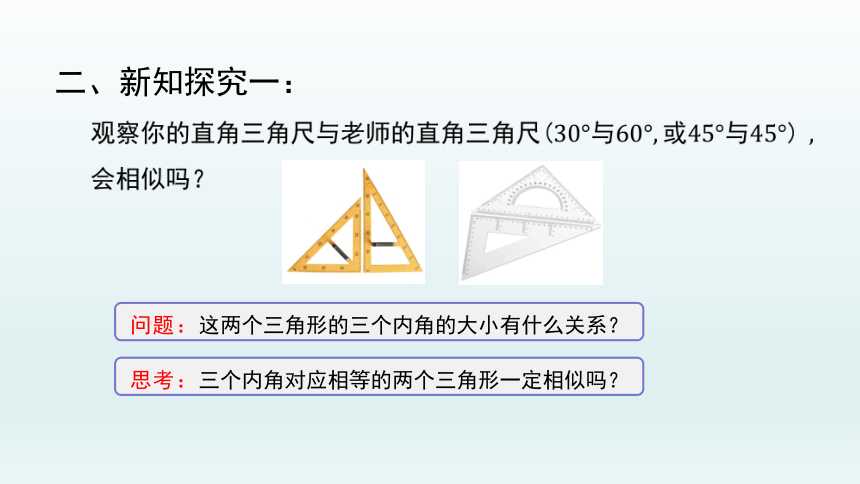
问题:这两个三角形的三个内角的大小有什么关系?
思考:三个内角对应相等的两个三角形一定相似吗?
二、新知探究一:
A
B
C
二、新知探究一:
A
B
C
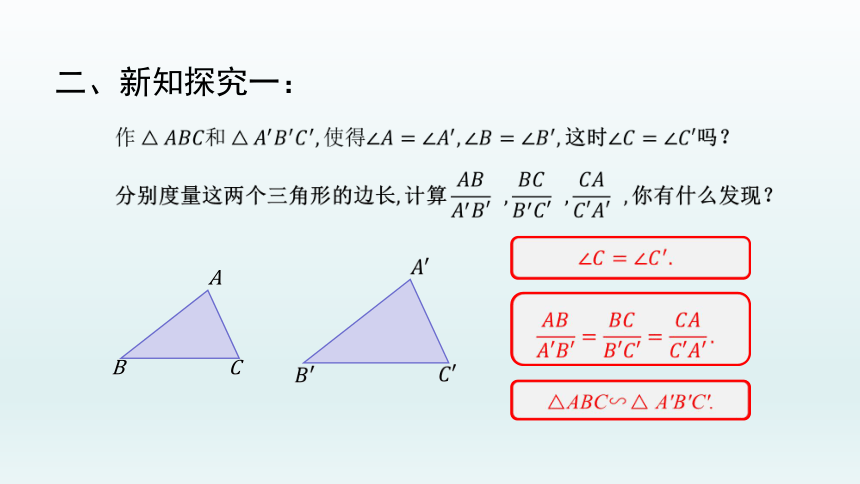
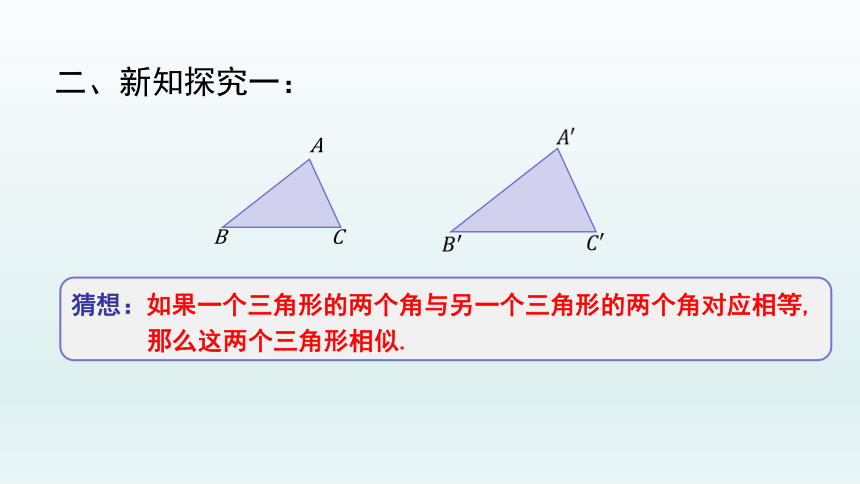
猜想:如果一个三角形的两个角与另一个三角形的两个角对应相等,
那么这两个三角形相似.
二、新知探究一:
A
B
C
D
E
A
B
C
如果一个三角形的两个角与另一个三角形的两个角对应相等,
那么这两个三角形相似.
相似三角形的判定(4)
两角分别相等的两个三角形相似.
∴△ABC∽△ A′B′C′.
几何语言:
A
D
E
C
B
相似三角形的判定.
相似三角形的性质.
如果两个直角三角形满足一个锐角相等,那么这两个直角三角形相似.
判定(4):两角分别相等的两个三角形相似.
判定(3):两边成比例且夹角相等的两个三角形相似.
如果两个直角三角形满足两组直角边成比例,那么这两个直角三角形相似.
判定两个直角三角形相似还有其它方法吗?
二、新知探究二:
思考:我们知道,两个直角三角形全等可以用“HL”来判定,那么,满足
斜边和一条直角边成比例的两个直角三角形相似吗?
A
B
C
A
B
C
二、新知探究二:
若 设
A
B
C
如果两个直角三角形的斜边和一条直角边成比例,
那么这两个直角三角形相似.
斜边和一条直角边成比例的两个直角三角形相似.
直角三角形相似的判定
几何语言:
A
B
C
D
A
B
C
E
1
2
巩固练习2.(1)底角相等的两个等腰三角形是否相似?
(2)顶角相等的两个等腰三角形呢?证明你的结论.
底角相等的两个等腰三角形是否相似?
A
B
C
底角相等的两个等腰三角形相似.
A
B
C
顶角相等的两个等腰三角形是否相似?
顶角相等的两个等腰三角形相似.
顶角相等的两个等腰三角形是否相似?
A
B
C
顶角相等的两个等腰三角形相似
A
D
C
B
A
D
C
B
A
D
C
B
A
D
C
B
A
B
C
D
相似三角形的判定.
相似三角形的性质.
A
E
F
B
C
D
三、课堂小结:
1.通过本节课的学习,你学到了哪些判定三角形相似的方法?
相似三角形的判定(4):两角分别相等的两个三角形相似.
2.你认为证明本节课中的判定定理的思路是什么?
直角三角形相似的判定:斜边和一条直角边成比例的两个直角三角形相似.
三、课堂小结:
判定(1):平行于三角形一边的直线和其他两边(或延长线)相交,
所构成的三角形与原三角形相似.
判定(2):三边成比例的两个三角形相似.
判定(3):两边成比例且夹角相等的两个三角形相似.
通过定义 :三个角分别相等,三条边成比例的两个三角形相似.
判定(4):两角分别相等的两个三角形相似.
相似三角形的判定方法:
3.相似三角形的判定方法有哪些?
谢谢
相似三角形的判定(4)
一、学习目标:
1.理解三角形相似的判定定理——“两角分别相等的两个三角形相似”;
2.理解判定直角三角形相似的特殊方法——“斜边和一条直角边成比例的两个直角三角形相似”;
3.会运用三角形相似的判定定理解决简单问题.
二、学习重点:
掌握运用三角形相似的判定定理解决简单问题.
一、复习引入:
通过定义 :三个角分别相等,三条边成比例的两个三角形相似.
回忆:目前我们知道哪些判定两个三角形相似的方法
一、复习引入:
判定(1):平行于三角形一边的直线和其他两边(或延长线)相交,所构成的三角形与原三角形相似.
回忆:目前我们知道哪些判定两个三角形相似的方法
一、复习引入:
回忆:目前我们知道哪些判定两个三角形相似的方法
∵
判定(2):三边成比例的两个三角形相似.
一、复习引入:
回忆:目前我们知道哪些判定两个三角形相似的方法
∵
判定(3):两边成比例且夹角相等的两个三角形相似.
回忆:目前我们知道哪些判定两个三角形相似的方法
一、复习引入:
判定(1):平行于三角形一边的直线和其他两边(或延长线)相交,
所构成的三角形与原三角形相似.
判定(2):三边成比例的两个三角形相似.
判定(3):两边成比例且夹角相等的两个三角形相似.
通过定义 :三个角分别相等,三条边成比例的两个三角形相似.
判定两个三角形相似还有其他方法吗
二、新知探究一:
问题:这两个三角形的三个内角的大小有什么关系?
思考:三个内角对应相等的两个三角形一定相似吗?
二、新知探究一:
A
B
C
二、新知探究一:
A
B
C
猜想:如果一个三角形的两个角与另一个三角形的两个角对应相等,
那么这两个三角形相似.
二、新知探究一:
A
B
C
D
E
A
B
C
如果一个三角形的两个角与另一个三角形的两个角对应相等,
那么这两个三角形相似.
相似三角形的判定(4)
两角分别相等的两个三角形相似.
∴△ABC∽△ A′B′C′.
几何语言:
A
D
E
C
B
相似三角形的判定.
相似三角形的性质.
如果两个直角三角形满足一个锐角相等,那么这两个直角三角形相似.
判定(4):两角分别相等的两个三角形相似.
判定(3):两边成比例且夹角相等的两个三角形相似.
如果两个直角三角形满足两组直角边成比例,那么这两个直角三角形相似.
判定两个直角三角形相似还有其它方法吗?
二、新知探究二:
思考:我们知道,两个直角三角形全等可以用“HL”来判定,那么,满足
斜边和一条直角边成比例的两个直角三角形相似吗?
A
B
C
A
B
C
二、新知探究二:
若 设
A
B
C
如果两个直角三角形的斜边和一条直角边成比例,
那么这两个直角三角形相似.
斜边和一条直角边成比例的两个直角三角形相似.
直角三角形相似的判定
几何语言:
A
B
C
D
A
B
C
E
1
2
巩固练习2.(1)底角相等的两个等腰三角形是否相似?
(2)顶角相等的两个等腰三角形呢?证明你的结论.
底角相等的两个等腰三角形是否相似?
A
B
C
底角相等的两个等腰三角形相似.
A
B
C
顶角相等的两个等腰三角形是否相似?
顶角相等的两个等腰三角形相似.
顶角相等的两个等腰三角形是否相似?
A
B
C
顶角相等的两个等腰三角形相似
A
D
C
B
A
D
C
B
A
D
C
B
A
D
C
B
A
B
C
D
相似三角形的判定.
相似三角形的性质.
A
E
F
B
C
D
三、课堂小结:
1.通过本节课的学习,你学到了哪些判定三角形相似的方法?
相似三角形的判定(4):两角分别相等的两个三角形相似.
2.你认为证明本节课中的判定定理的思路是什么?
直角三角形相似的判定:斜边和一条直角边成比例的两个直角三角形相似.
三、课堂小结:
判定(1):平行于三角形一边的直线和其他两边(或延长线)相交,
所构成的三角形与原三角形相似.
判定(2):三边成比例的两个三角形相似.
判定(3):两边成比例且夹角相等的两个三角形相似.
通过定义 :三个角分别相等,三条边成比例的两个三角形相似.
判定(4):两角分别相等的两个三角形相似.
相似三角形的判定方法:
3.相似三角形的判定方法有哪些?
谢谢
