平行线等分线段定理[下学期]
文档属性
| 名称 | 平行线等分线段定理[下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 60.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-03-02 00:00:00 | ||
图片预览




文档简介
课件13张PPT。平行线等分线段定理:平行线等分线段定理:如果一组平行线在一条直线上截得
的线段相等,那么在其它直线上截
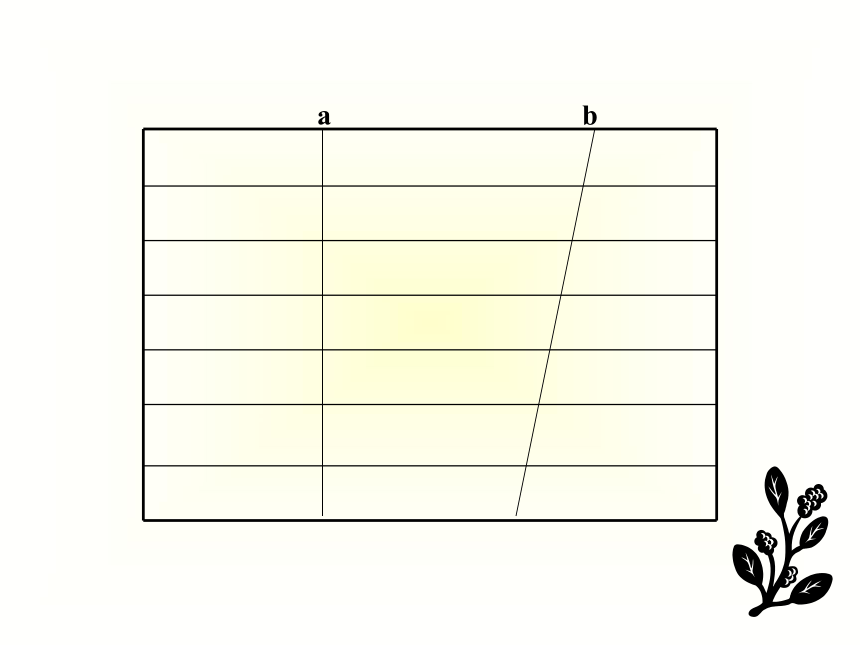
得的线段也相等。思考:我们学过有关平行线的那些知识?1 )平行线的三线八角 。2)平行线间的平行线段 。 已知:直线a//b//c,AB=BC.
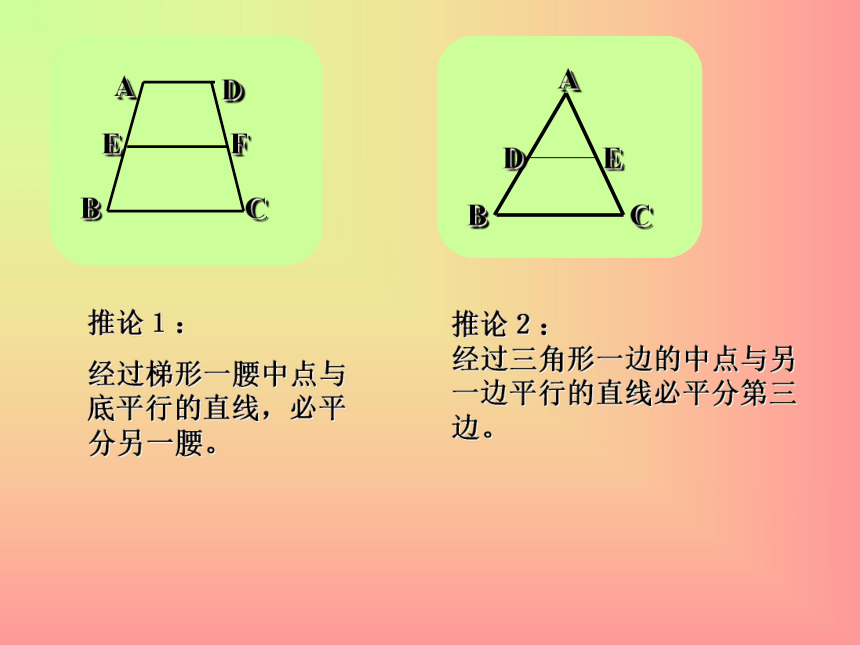
求证:DE=EFEG=EHDE=EF分析过程:推论1:
经过梯形一腰中点与底平行的直线,必平分另一腰。推论2:
经过三角形一边的中点与另
一边平行的直线必平分第三
边。例题讲解:已知:线段AB
求作:线段AB的五等分点。作法:1)作射线AC。
4)过点G、F、E、D分别作HB的平行线
GL、FK、EJ、DI,分别交AB于
点L、K、J、I。
L、K、J、I就是所求的五等分点
2)在射线AC上顺次截取
AD=DE=EF=FG=GH。
3)连结HB。
例2:如图,平行四边形ABCD中,
BC与AD的中点分别为E、F,
且BF、DE、与对角线AC交于H、G。
求证:AH=HG=GC 例3:如图,在三角形ABC中,在CA的延
长线上取一点D,使DA=1/2CA,E
为BC的中点,DE交AB于F,过F引
FG垂直于DE与CB的延长线交于G。
求证:GD=GE证明证明:
四边形ABCD是平行四边形
AD//BC
AD=BCDF=1/2AD
BE=1/2BC四边形FDEB是平行四边形 BF//DEAF=DFAH=HG 同理CG=HGAH=HG=CG练习题1) 如图:AD是三角形ABC的中线,E为AD的中点, BE的延长线交AC于F, 求证:AF=1/3AC
2)如图 ,已知AC AB,DB AB,O为CD中点,
求证:OA=OB
3)如图,在梯形ABCD中,AB//DC,以AC、AD为边作平行四边形ACED,DC的延长线交BE于F,
求证:EF=BF
的线段相等,那么在其它直线上截
得的线段也相等。思考:我们学过有关平行线的那些知识?1 )平行线的三线八角 。2)平行线间的平行线段 。 已知:直线a//b//c,AB=BC.
求证:DE=EFEG=EHDE=EF分析过程:推论1:
经过梯形一腰中点与底平行的直线,必平分另一腰。推论2:
经过三角形一边的中点与另
一边平行的直线必平分第三
边。例题讲解:已知:线段AB
求作:线段AB的五等分点。作法:1)作射线AC。
4)过点G、F、E、D分别作HB的平行线
GL、FK、EJ、DI,分别交AB于
点L、K、J、I。
L、K、J、I就是所求的五等分点
2)在射线AC上顺次截取
AD=DE=EF=FG=GH。
3)连结HB。
例2:如图,平行四边形ABCD中,
BC与AD的中点分别为E、F,
且BF、DE、与对角线AC交于H、G。
求证:AH=HG=GC 例3:如图,在三角形ABC中,在CA的延
长线上取一点D,使DA=1/2CA,E
为BC的中点,DE交AB于F,过F引
FG垂直于DE与CB的延长线交于G。
求证:GD=GE证明证明:
四边形ABCD是平行四边形
AD//BC
AD=BCDF=1/2AD
BE=1/2BC四边形FDEB是平行四边形 BF//DEAF=DFAH=HG 同理CG=HGAH=HG=CG练习题1) 如图:AD是三角形ABC的中线,E为AD的中点, BE的延长线交AC于F, 求证:AF=1/3AC
2)如图 ,已知AC AB,DB AB,O为CD中点,
求证:OA=OB
3)如图,在梯形ABCD中,AB//DC,以AC、AD为边作平行四边形ACED,DC的延长线交BE于F,
求证:EF=BF
