平面直角坐标系“阶段测评”试卷(上一题目,下一答案)
文档属性
| 名称 | 平面直角坐标系“阶段测评”试卷(上一题目,下一答案) |
|
|
| 格式 | rar | ||
| 文件大小 | 401.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-03-20 00:00:00 | ||
图片预览


文档简介
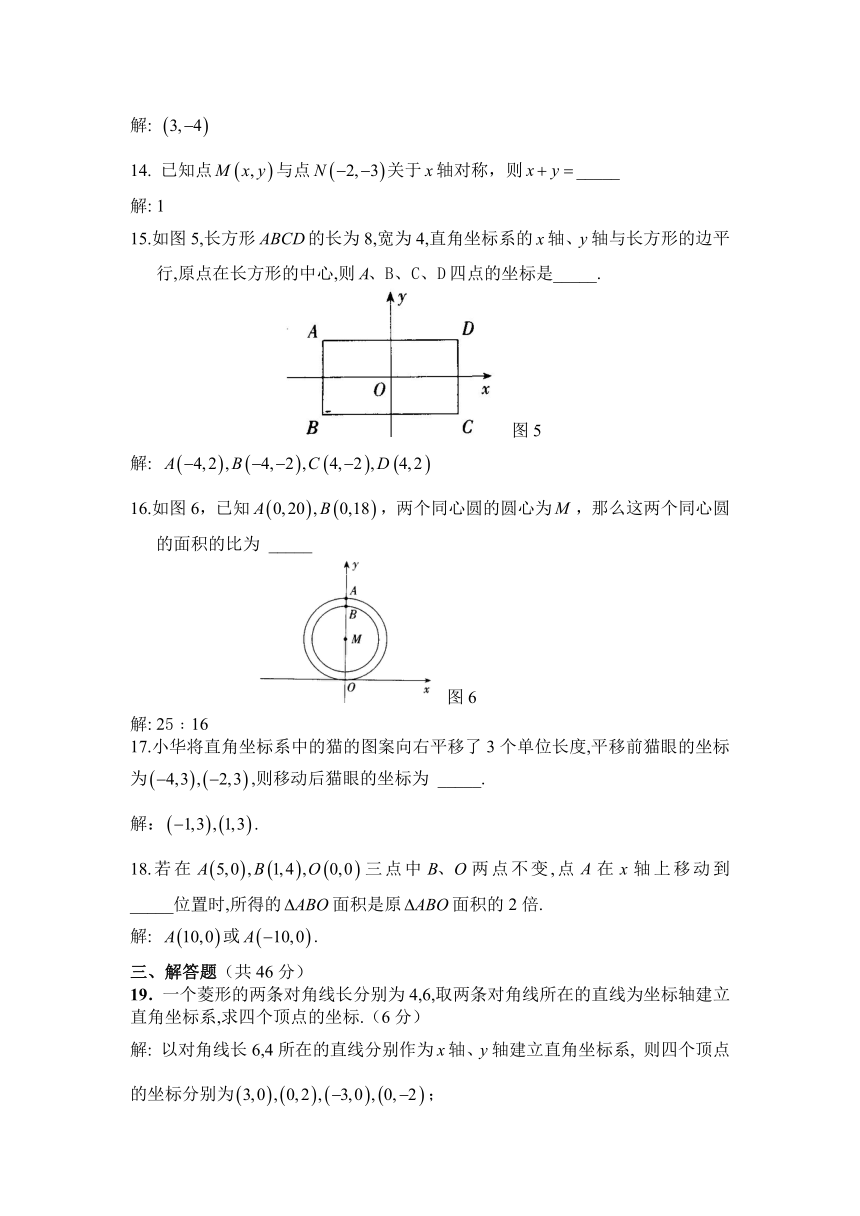
七年级(人教版)平面直角坐标系“阶段测评”试卷
命题:钟国雄(中国数学奥林匹克一级教练,中学高级教师)
电话:0755-21017520 13699770520 13008808214
一、选择题(每题3分,共24分)
1.课间操时,小华、小军、小刚的位置如图1,小李对小刘说:“如果我的位置用表示,小马的位置用表示,那么你的位置可以表示成( )”
(A) (B) (C) (D)
图1
解: (D)
2.如图2,下列说法正确的是( )
(A)与的横坐标相同 (B)与的横坐标相同
(C)与的纵坐标相同 (D)与的纵坐标相同
图2
解: (C)
3.点位于轴下方,距轴4个单位,且位于轴左方,距轴3个单位,则点的坐标是( )
(A) (B) (C) (D)
解:(C)
4.若表示同一个点,那么这一点在( )
(A)第二、四象限内两坐标轴夹角平分线上(B)平行于轴的直线上
(C)平行于轴的直线上 (D)第一、三象限内两坐标轴夹角平分线上
解: (D)
5.点在第四象限,则在( )
(A)第一象限(B)第二象限(C)第三象限(D)第四象限
解: (B)
6.在直角坐标系中,适合条件的点的个数为( )
(A)1个 (B)2个 (C)4个 (D)8个
解:(C)
7. 已知点和点关于轴对称,则的值为( ).
(A)0 (B) (C)1 (D)
解:(C)
8. 已知两圆的圆心都在轴上,为两圆的交点,若点的坐标为,则点的坐标为( ).
(A) (B) (C) (D)
解: (A)
二、填空题(每题3分,共30分)
9.如图3,是小刚画的一张脸,他对妹妹说:“如果我用表示左眼,用表示右脸,那么嘴的位置可以表示成_____”.
图3
解:
10.在平面直角坐标系中,点关于原点的对称的点的坐标在第 ____象限.
解:三
11.若点在轴上,则 ____.
解:
12.如图4,小强告诉小华图中两点的坐标分别为,小华一下子就说出了在同一坐标系下的坐标为_____.
图4
解:
13. 若点是第四象限中的点,且,则点的坐标是_____.
解:
14. 已知点与点关于轴对称,则_____
解: 1
15.如图5,长方形的长为8,宽为4,直角坐标系的轴、轴与长方形的边平行,原点在长方形的中心,则四点的坐标是_____.
图5
解:
16.如图6,已知,两个同心圆的圆心为,那么这两个同心圆的面积的比为 _____
图6
解: 25﹕16
17.小华将直角坐标系中的猫的图案向右平移了3个单位长度,平移前猫眼的坐标为,则移动后猫眼的坐标为 _____.
解:.
18.若在三点中两点不变,点在轴上移动到 _____位置时,所得的面积是原面积的2倍.
解: 或.
三、解答题(共46分)
19.一个菱形的两条对角线长分别为4,6,取两条对角线所在的直线为坐标轴建立直角坐标系,求四个顶点的坐标.(6分)
解: 以对角线长6,4所在的直线分别作为轴、轴建立直角坐标系, 则四个顶点的坐标分别为;
若以对角线长4,6所在的直线分别作为轴、轴建立直角坐标系,则四个顶点的坐标则分别为.
20. 在平面直角坐标系中画出下列各点:,观察这些点的位置,你发现了什么规律?(6分)
图7
解:各点如图7所示.
由于四点的纵坐标都是,因此这四个点都在过点,平行于轴的一条直线上,这条直线上任意一点的纵坐标都是.
平行于轴的直线上的点的纵坐标相等, 平行于轴的直线上的点的横坐标相等.
21.在平面直角坐标系中画出下列各点:.说出这些点的坐标有什么特点,画出的这些点有什么规律 在平面直角坐标系中,第二、四象限的角平分线上的点又有什么特点 (6分)
图8
解: 各点如图8所示.
各点的横坐标与纵坐标相等.这些点都在一条直线上,这条直线是
第一、三象限的角平分线.而且第一、三象限的角的平分线上的任意一点的横坐标与纵坐标都相等.
在平面直角坐标系中, 第二、四象限的角的平分线上的点的横坐标与纵坐标互为相反数.
22. 观察图9中的两个正方形,这两个正方形是怎样变化的,按照这个规律,第三个正方形的四个顶点的坐标是什么 (至少写出三种规律变化)(6分)
图9
解:原图中的两个正方形的四个顶点的坐标分别是和.
规律一: 从小正方形到大正方形看,每一个顶点的横坐标、纵坐标都增加一个单位,则第三个正方形的四个顶点的坐标是;
规律二: 从小正方形到大正方形看,每一个顶点的横坐标、纵坐标都扩大到原来的2倍, 则第三个正方形的四个顶点的坐标是;
规律三: 从大正方形到小正方形看,每一个顶点的横坐标、纵坐标都缩小到原来的,则第三个正方形的四个顶点的坐标是.
23.如图10,这是某市部分简图,请建立适当的平面直角坐标系,分别写出各地的坐标 (7分)
图10
解:如果火车站用表示,则医院的坐标为,文化宫的坐标为,体育场的坐标为,宾馆的坐标为,市场的坐标为,超市的坐标为.
注意:本题答案不唯一.
24. 在平面直角坐标系中画出四个点,依次连接,这是一个什么图形 把这个图形向右平移五个单位,各顶点依次为写出这四个点的坐标,并说出在这次平移的过程中坐标是怎样变化的.
再把得到的图形向下平移三个单位,写出平移后的坐标,并说出在第二次平移的过程中坐标是怎样变化的.你找到了什么规律 (7分)
图11
解: 如图11,是一个正方形.
向右平移五个单位后各顶点的坐标依次为,在这次平移的过程中各点的横坐标依次增加5,纵坐标不变.
再向下平移三个单位后各顶点的坐标依次为,在这次平移的过程中各点的横坐标不变,纵坐标依次减3.
当一个图形中各顶点的横坐标都加上同一个正数时,图形向右平移个单位,若都减去同一个正数,图形向左平移个单位; 当一个图形中各顶点的纵坐标都加上同一个正数时,图形向上平移个单位,若都减去同一个正数,图形向下平移个单位.
25. 已知两点的坐标,如图12所示,求的面积.(8分)
图12
解: 如图13所示,过点作轴的垂线,垂足为,过作轴的垂线,垂足为,两垂线交于点,则四边形是长方形,由点的坐标可知,
.
所以,
图13
命题:钟国雄(中国数学奥林匹克一级教练,中学高级教师)
电话:0755-21017520 13699770520 13008808214
一、选择题(每题3分,共24分)
1.课间操时,小华、小军、小刚的位置如图1,小李对小刘说:“如果我的位置用表示,小马的位置用表示,那么你的位置可以表示成( )”
(A) (B) (C) (D)
图1
解: (D)
2.如图2,下列说法正确的是( )
(A)与的横坐标相同 (B)与的横坐标相同
(C)与的纵坐标相同 (D)与的纵坐标相同
图2
解: (C)
3.点位于轴下方,距轴4个单位,且位于轴左方,距轴3个单位,则点的坐标是( )
(A) (B) (C) (D)
解:(C)
4.若表示同一个点,那么这一点在( )
(A)第二、四象限内两坐标轴夹角平分线上(B)平行于轴的直线上
(C)平行于轴的直线上 (D)第一、三象限内两坐标轴夹角平分线上
解: (D)
5.点在第四象限,则在( )
(A)第一象限(B)第二象限(C)第三象限(D)第四象限
解: (B)
6.在直角坐标系中,适合条件的点的个数为( )
(A)1个 (B)2个 (C)4个 (D)8个
解:(C)
7. 已知点和点关于轴对称,则的值为( ).
(A)0 (B) (C)1 (D)
解:(C)
8. 已知两圆的圆心都在轴上,为两圆的交点,若点的坐标为,则点的坐标为( ).
(A) (B) (C) (D)
解: (A)
二、填空题(每题3分,共30分)
9.如图3,是小刚画的一张脸,他对妹妹说:“如果我用表示左眼,用表示右脸,那么嘴的位置可以表示成_____”.
图3
解:
10.在平面直角坐标系中,点关于原点的对称的点的坐标在第 ____象限.
解:三
11.若点在轴上,则 ____.
解:
12.如图4,小强告诉小华图中两点的坐标分别为,小华一下子就说出了在同一坐标系下的坐标为_____.
图4
解:
13. 若点是第四象限中的点,且,则点的坐标是_____.
解:
14. 已知点与点关于轴对称,则_____
解: 1
15.如图5,长方形的长为8,宽为4,直角坐标系的轴、轴与长方形的边平行,原点在长方形的中心,则四点的坐标是_____.
图5
解:
16.如图6,已知,两个同心圆的圆心为,那么这两个同心圆的面积的比为 _____
图6
解: 25﹕16
17.小华将直角坐标系中的猫的图案向右平移了3个单位长度,平移前猫眼的坐标为,则移动后猫眼的坐标为 _____.
解:.
18.若在三点中两点不变,点在轴上移动到 _____位置时,所得的面积是原面积的2倍.
解: 或.
三、解答题(共46分)
19.一个菱形的两条对角线长分别为4,6,取两条对角线所在的直线为坐标轴建立直角坐标系,求四个顶点的坐标.(6分)
解: 以对角线长6,4所在的直线分别作为轴、轴建立直角坐标系, 则四个顶点的坐标分别为;
若以对角线长4,6所在的直线分别作为轴、轴建立直角坐标系,则四个顶点的坐标则分别为.
20. 在平面直角坐标系中画出下列各点:,观察这些点的位置,你发现了什么规律?(6分)
图7
解:各点如图7所示.
由于四点的纵坐标都是,因此这四个点都在过点,平行于轴的一条直线上,这条直线上任意一点的纵坐标都是.
平行于轴的直线上的点的纵坐标相等, 平行于轴的直线上的点的横坐标相等.
21.在平面直角坐标系中画出下列各点:.说出这些点的坐标有什么特点,画出的这些点有什么规律 在平面直角坐标系中,第二、四象限的角平分线上的点又有什么特点 (6分)
图8
解: 各点如图8所示.
各点的横坐标与纵坐标相等.这些点都在一条直线上,这条直线是
第一、三象限的角平分线.而且第一、三象限的角的平分线上的任意一点的横坐标与纵坐标都相等.
在平面直角坐标系中, 第二、四象限的角的平分线上的点的横坐标与纵坐标互为相反数.
22. 观察图9中的两个正方形,这两个正方形是怎样变化的,按照这个规律,第三个正方形的四个顶点的坐标是什么 (至少写出三种规律变化)(6分)
图9
解:原图中的两个正方形的四个顶点的坐标分别是和.
规律一: 从小正方形到大正方形看,每一个顶点的横坐标、纵坐标都增加一个单位,则第三个正方形的四个顶点的坐标是;
规律二: 从小正方形到大正方形看,每一个顶点的横坐标、纵坐标都扩大到原来的2倍, 则第三个正方形的四个顶点的坐标是;
规律三: 从大正方形到小正方形看,每一个顶点的横坐标、纵坐标都缩小到原来的,则第三个正方形的四个顶点的坐标是.
23.如图10,这是某市部分简图,请建立适当的平面直角坐标系,分别写出各地的坐标 (7分)
图10
解:如果火车站用表示,则医院的坐标为,文化宫的坐标为,体育场的坐标为,宾馆的坐标为,市场的坐标为,超市的坐标为.
注意:本题答案不唯一.
24. 在平面直角坐标系中画出四个点,依次连接,这是一个什么图形 把这个图形向右平移五个单位,各顶点依次为写出这四个点的坐标,并说出在这次平移的过程中坐标是怎样变化的.
再把得到的图形向下平移三个单位,写出平移后的坐标,并说出在第二次平移的过程中坐标是怎样变化的.你找到了什么规律 (7分)
图11
解: 如图11,是一个正方形.
向右平移五个单位后各顶点的坐标依次为,在这次平移的过程中各点的横坐标依次增加5,纵坐标不变.
再向下平移三个单位后各顶点的坐标依次为,在这次平移的过程中各点的横坐标不变,纵坐标依次减3.
当一个图形中各顶点的横坐标都加上同一个正数时,图形向右平移个单位,若都减去同一个正数,图形向左平移个单位; 当一个图形中各顶点的纵坐标都加上同一个正数时,图形向上平移个单位,若都减去同一个正数,图形向下平移个单位.
25. 已知两点的坐标,如图12所示,求的面积.(8分)
图12
解: 如图13所示,过点作轴的垂线,垂足为,过作轴的垂线,垂足为,两垂线交于点,则四边形是长方形,由点的坐标可知,
.
所以,
图13
