2022-2023学年人教版八年级数学上册12.2三角形全等的判定解答题专题提升训练(含答案)
文档属性
| 名称 | 2022-2023学年人教版八年级数学上册12.2三角形全等的判定解答题专题提升训练(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 557.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-09 21:09:45 | ||
图片预览




文档简介
2022-2023学年人教版八年级数学上册《12.2三角形全等的判定》
解答题专题提升训练(附答案)
1.如图,C、E分别在AB、DF上,O是CF的中点,EO=BO,求证:∠ACE+∠DEC=180°.
证明:∵O是CF的中点,
∴ = ,
在△COB和△FOE中,
.
∴△COB≌△FOE ( ),
∴∠ =∠ ,( ).
∴AB∥DF,( ).
∴∠ACE+∠DEC=180°.( ).
2.如图,在四边形ABCD中,AD∥BC,点E为对角线BD上一点,∠A=∠BEC,且AD=BE.
(1)求证:△ABD≌△ECB;
(2)若∠BDC=70°,求∠DBC的度数.
3.如图,在△ABC中,点D在AC上,BD平分∠ABC,延长BA到点E,使得BE=BC,连接DE,若∠ADE=38°,∠C=42°,求∠BAD的度数.
4.如图所示,点E在△ABC外部,点D在BC边上,DE交AC于F,若∠1=∠3,∠E=∠C,AE=AC,问△ABC≌△ADE吗?请说明理由.
5.如图,△AOB≌△COD,OD与AB交于点G,OB与CD交于点E.
(1)∠AOD与∠COB的数量关系是:∠AOD ∠COB;
(2)求证:△AOG≌△COE;
(3)若OA=OB,当A,O,C三点共线时,恰好OB⊥CD,则此时∠AOB= °.
6.△ABC和△ADE如图所示,其中∠ABC=∠ACB,∠ADE=∠AED,∠BAC=∠DAE.
(1)如图①,连接BE、CD,求证:BE=CD;
(2)如图②,连接BE、CD、BD,若∠BAC=∠DAE=60°,CD⊥AE,AD=3,CD=5,求BD的长.
7.如图,点C、E、F、B在同一直线上,点A、D在BC异侧,AB∥CD,AB=CD,BF=CE.
(1)试说明:∠A=∠D;
(2)若AB=CF,∠A比∠B的余角大20°,求∠D的度数.
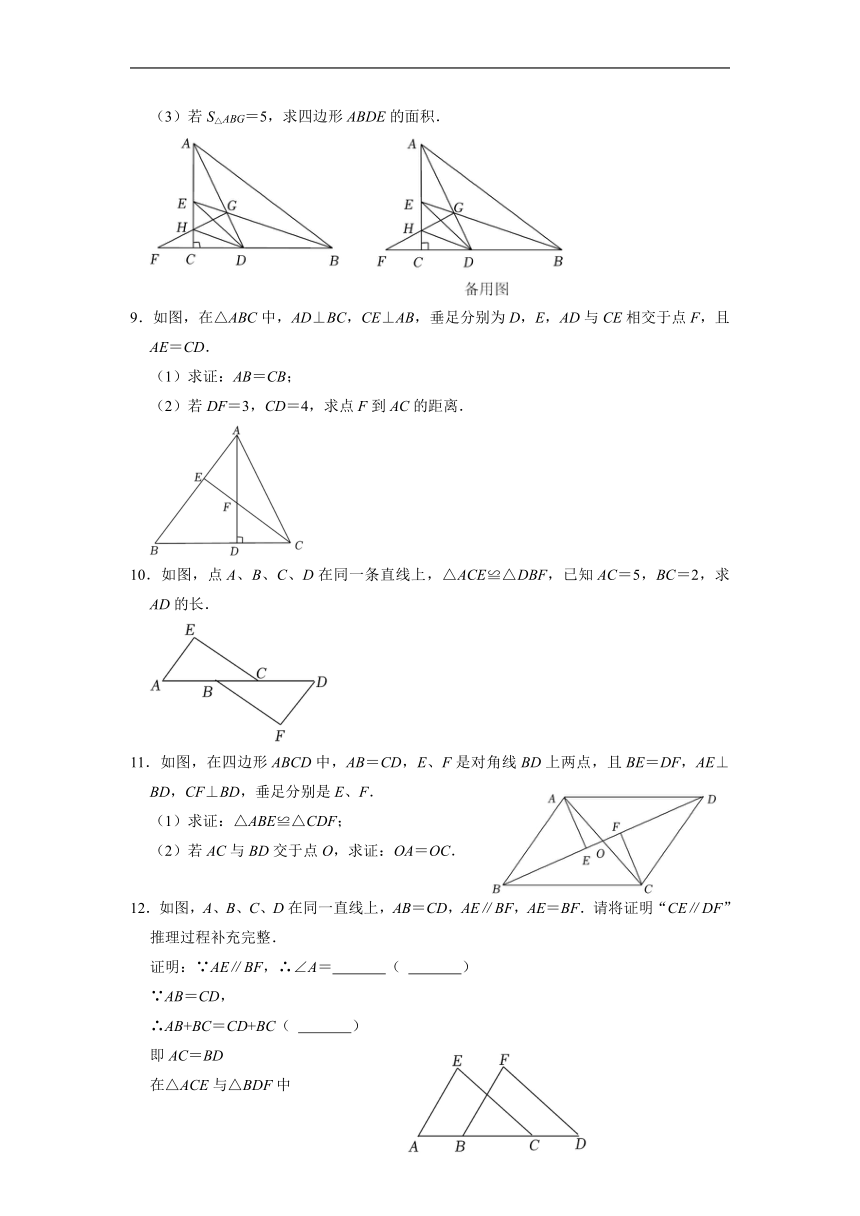
8.如图,Rt△ACB中,∠ACB=90°,∠CAB与∠ABC的角平分线BE,AD相交于点G,过G作AD垂线交BC的延长线于点F,交AC于点H.
(1)求∠DGB的大小;
(2)若AD=10,GF=6,求GH长度;
(3)若S△ABG=5,求四边形ABDE的面积.
9.如图,在△ABC中,AD⊥BC,CE⊥AB,垂足分别为D,E,AD与CE相交于点F,且AE=CD.
(1)求证:AB=CB;
(2)若DF=3,CD=4,求点F到AC的距离.
10.如图,点A、B、C、D在同一条直线上,△ACE≌△DBF,已知AC=5,BC=2,求AD的长.
11.如图,在四边形ABCD中,AB=CD,E、F是对角线BD上两点,且BE=DF,AE⊥BD,CF⊥BD,垂足分别是E、F.
(1)求证:△ABE≌△CDF;
(2)若AC与BD交于点O,求证:OA=OC.
12.如图,A、B、C、D在同一直线上,AB=CD,AE∥BF,AE=BF.请将证明“CE∥DF”推理过程补充完整.
证明:∵AE∥BF,∴∠A= ( )
∵AB=CD,
∴AB+BC=CD+BC( )
即AC=BD
在△ACE与△BDF中
∴△ACE≌△BDF( )
∴ ( )
∴CE∥DF( )
13.如图,△ABC中,∠ABC=45°,D为BC上一点,∠ADC=60°,AE⊥BC于点E,CF⊥AD于点F,AE、CF相交于点G,∠CAE=15°.
(1)求∠ACF的度数;
(2)求证:DF=AG.
14.如图,点D为△ABC边AC上一点,过点D作DE∥AB,点O为BE的中点,连接AO并延长,交DE的延长线于点F,连接AE、BF.
(1)试判断四边形ABFE的形状,并说明理由;
(2)若AB=BF,AC=10,∠C=30°,求OC的长.
15.如图,A,E,F,B在同一条直线上,CE⊥AB,DF⊥AB,垂足分别为E,F,AE=BF,∠A=∠B.
(1)求证:△ADF≌△BCE.
(2)当BC⊥AD时,,OA=3时,求OD的长.
16.已知AB=AC,AD=AE,∠BAC=∠DAE.
(1)如图1,当点D在BC上时,求证:BD=CE;
(2)如图2,当点D、E、C在同一直线上,且∠BAC=α,∠BAE=β时,求∠DBC的度数(用含α和β的式子表示).
17.如图,在四边形ABCD中,点E为对角线BD上一点,∠A=∠BEC,∠ABD=∠BCE,且AD=BE.
(1)证明:①△ABD≌△ECB;②AD∥BC;
(2)若BC=15,AD=6,请求出DE的长度.
18.如图,已知点A、C分别在∠GBE的边BG、BE上,且AB=AC,AD∥BE,与∠ACE的平分线CD交于点D,连接BD.求证:BD平分∠ABC.
19.小明利用一根长3 m的竿子来测量路灯AB的高度.他的方法如下:如图,在路灯前选一点P,使BP=3m,并测得∠APB=70°,然后把竖直的竿子CD(CD=3m)在BP的延长线上左右移动,使∠CPD=20°,此时测得BD=11.2m.请根据这些数据,计算出路灯AB的高度.
20.已知AC、BD相交于点O,OA=OC,OB=OD.
(1)求证:△AOB≌△COD;
(2)连接BC,若AB=8,BC=10,求OB的取值范围.
21.如图,长方形ABCD中,AB=4cm,BC=6cm,现有一动点P从A出发以2cm/秒的速度,沿矩形的边A﹣B﹣C﹣D﹣A返回到点A停止,设点P运动的时间为t秒.
(1)当t=3时,BP= cm;
(2)当t为何值时,连接CP,DP,△CDP是等腰三角形;
(3)Q为AD边上的点,且DQ=5,当t为何值时,以长方形的两个顶点及点P为顶点的三角形与△DCQ全等.
22.如图,已知四边形ABCD中,AB=BC=8cm,CD=6cm,∠B=∠C,动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速运动,点Q运动的速度是每秒2cm,点P运动的速度是每秒acm(a≤2),当点Q到达点C时,P、Q两点都停止运动,设运动时间为t秒.
(1)BQ= ,BP= .(用含a或t的代数式表示)
(2)运动过程中,连接PQ,DQ,△BPQ与△CDQ能否全等?若能,请求出相应的t和a的值,若不能,说明理由.
23.如图,已知△ABC中,∠B=∠C,AB=8,BC=6,点D为AB的中点,如果点P在线段BC上以每秒2个单位长度的速度由B点向C点运动,同时,点Q在线段CA上以每秒a个单位长度的速度由C点向A点运动,设运动时间为t(秒)(0≤t≤3)
(1)PC= (用含t的代数式表示);
(2)若点P、Q的运动速度相等,经过1秒后,△BPD与△CQP是否全等,请说明理由;
(3)若点P、Q的运动速度不相等,当点Q的运动速度a= 时,能够使△BPD与△CQP全等.
24.已知正方形ABCD中,边长为10cm,点E在AB边上,BE=6cm,如果点P在线段BC上以4cm/s的速度由点B向点C运动,同时点Q在线段CD上以acm/的速度由点C向点D运动,设运动的时间为t秒,
(1)CP的长为 cm(用含t的代数式表示)
(2)若以E、B、P为顶点的三角形和以P、C、Q为顶点的三角形全等,求a的值
25.如图,已知△ABC中,AB=AC=24厘米,∠ABC=∠ACB,BC=16厘米,点D为AB的中点.如果点P在线段BC上以4厘米/秒的速度由B点向C点运动.同时,点Q在线段CA上由C点以a厘米/秒的速度向A点运动.设运动的时间为t秒.
(1)直接写出:
①BD= 厘米; ②BP= 厘米;
③CP= 厘米; ④CQ= 厘米;
(可用含t、a的代数式表示)
(2)若以D,B,P为顶点的三角形和以P,C,Q为顶点的三角形全等,试求a、t的值.
26.如图,在矩形ABCD中,AD=3,DC=5,动点M从A点出发沿线段AD﹣DC以每秒1个单位长度的速度向终点C运动;动点N同时从C点出发沿线段CD﹣DA以每秒3个单位长度的速度向终点A运动.ME⊥PQ于点E,NF⊥PQ于点F,设运动的时间为t秒.
(1)在运动过程中当M、N两点相遇时,求t的值.
(2)在整个运动过程中,求DM的长.(用含t的代数式表示)
(3)当△DEM与△DFN全等时,请直接写出所有满足条件的DN的长.
27.如图,在△ABC中,AB=AC=18cm,BC=10cm,AD=2BD.动点P以2cm/s的速度沿射线BC运动,同时,点Q从点C出发,以acm/s的速度向终点A运动,当Q点停止运动时,P点也随之停止运动,设点P的运动时间为t(s)(t>0).
(1)用含t的代数式表示PC的长;
(2)若点Q的运动速度为1cm/s,当△CQP是以∠C为顶角的等腰三角形时,求t的值;
(3)当点Q的运动速度为多少时,能使△BPD与△CQP在某一时刻全等.
参考答案
1.证明:∵O是CF的中点,
∴CO=FO,
在△COB和△FOE中,
,
∴△COB≌△FOE(SAS),
∴∠OBC=∠OEF(全等三角形对应角相等),
∴AB∥DF(内错角相等,两直线平行),
∴∠ACE+∠DEC=180°(两直线平行,同旁内角互补).
故答案为:CO;FO;SAS;OBC;OEF;全等三角形对应角相等;内错角相等,两直线平行;两直线平行,同旁内角互补.
2.(1)证明:∵AD∥BC,
∴∠ADB=∠EBC,
在△ABD和△ECB中,
,
∴△ABD≌△ECB(ASA);
(2)解:∵△ABD≌△ECB,
∴BD=BC,
∴∠BDC=∠BCD=70°,
∴∠DBC=40°.
3.解:∵BD平分∠ABC,
∴∠EBD=∠CBD,
在△BDE和△BDC中,
,
∴△BDE≌△BDC(SAS),
∴∠E=∠C=42°,
∵∠ADE=38°,
∴∠BAD=∠ADE+∠E=38°+42°=80°.
4.解:△ABC和△ADE全等,
理由是:∵∠ADC=∠B+∠1=∠3+∠ADE,
又∵∠1=∠3,
∴∠B=∠ADE,
在△ABC和△ADE中,
,
∴△ABC≌△ADE(AAS),
即△ABC和△ADE全等.
5.(1)解:∵△AOB≌△COD,
∴∠AOB=∠COD,
∴∠AOB﹣∠BOD=∠COD﹣∠BOD,
即∠AOD=∠COB,
故答案为:=;
(2)证明:∵△AOB≌△COD,
∴OA=OC,∠A=∠C,
在△AOG和△COE中,
,
∴△AOG≌△COE(ASA);
(3)如图,∵△AOB≌△COD,
∴OA=OC,OB=OD,
∵OA=OB,
∴OA=OB=OC=OD,
∵OB⊥CD,
∴CE=DE,
∴OE是△ACD的中位线,
∴OE∥AD,
∴∠ODA=∠BOD,
∵OA=OD,
∴∠OAD=∠ODA,
∵∠OAD+∠ODA+∠AOD=∠BOD+∠BOC+∠AOD=180°,∠AOD=∠BOC,
∴∠AOD=∠BOD=∠BOC=60°,
∴∠AOB=120°,
故答案为:120.
6.(1)证明:∵∠ABC=∠ACB,∠ADE=∠AED,CAD
∴AB=AC,AE=AD,
∵,∠BAC=∠DAE,
∴∠BAE=∠CAD,
∴△ABE≌△ACD(SAS),
∴BE=CD.
(2)解:∵∠ADE=∠AED,
∴AE=AD,
∵∠DAE=60°,
∴△DAE是等边三角形,
∴AD=ED=3,∠AED=∠ADE=60°,
∵CD⊥AE,
∴∠ADC=×60°=30°,
由(1)知:△ABE≌△ACD,
∴BE=CD=5,∠AEB=∠ADC=30°,
∴∠BED=90°,
∴BD=.
7.解:(1)∵AB∥CD,
∴∠C=∠B,
∵CE=BF,
∴CE+EF=FB+EF,
即CF=BE,
在△AEB和△DFC中,
,
∴△AEB≌△DFC(SAS),
∴∠A=∠D;
(2)设∠B=x,则∠B的余角为90°﹣x,
∵∠A比∠B的余角大20°,
∴∠A=90°﹣x+20°=110°﹣x,
∵BE=CF,AB=CF,
∴AB=BE,
∴∠AEB=∠A=110°﹣x,
由三角形内角和为180°得:2(110°﹣x)+x=180°,
解得:x=40°,
∴∠D=∠A=110°﹣40°=70°.
8.解:(1)∵△ABC的角平分线AD、BE相交于点G,
∴∠GAB+∠GBA=(∠CAB+∠CBA)=45°,
∴∠DGB=∠GAB+∠ABG=45°;
(2)∵∠ACB=90°,
∴∠FCH=90°,
由(1)知:∠DGB=45°,
∴∠AGB=135°,
又∵GF⊥AD,
∴∠FGB=90°+45°=135°,
∴∠AGB=∠FGB,
∵∠AHG=∠CHF,∠AGH=∠FCH=90°,
∴∠BFH=∠CAD=∠BAD,
在△ABG和△FBG中,
,
∴△ABG≌△FBG(ASA),
∴GA=GF,
∵AD=10,GF=6,
∴DG=AD﹣AG=AD﹣FG=10﹣6=4,
∵∠F=∠CAD,∠AGH=∠FGD,AG=FG,
∴△AGH≌△FGD(AAS),
∴GH=DG=4;
(3)如图,
∵△ABG≌△FBG,△AGH≌△FGD,
∴S△AGB=S△FBG,S△AGH=S△FGD,GH=GD,
∵∠HGD=90°,
∴∠HDG=∠DHG=45°=∠BGD,
∴HD∥EG,
∴S△EGH=S△EGD,
∵S四边形ABDE=S△ABG+S△AEG+S△EGD+S△GBD=S△ABG+(S△AEG+S△EGH)+S△GBD
=S△ABG+S△FGD+S△GBD
=S△ABG+S△FBG
=2S△ABG
=2×5
=10.
9.证明:(1)∵AD⊥BC,CE⊥AB,
∴∠AEF=∠CDF=∠BEC=∠BDA=90°.
在△AEF和△CDF中,
∴△AEF≌△CDF(AAS),
∴EF=DF,AF=CF.
∴EF+CF=DF+AF,
∴EC=DA,
在△ABD和△CBE中,
∴△ABD≌△CBE(AAS),
∴AB=CB;
(2)∵△AEF≌△CDF,
∴AF=CF,
∵DF=3,CD=4,
∴在Rt△CDF中,CF=5,
∴AD=AF+DF=CF+DF=5+3=8,
在Rt△ADC中,AC=,
设点F到AC的距离为h,
∵,
∴,
∴点F到AC的距离为.
10.解:∵AC=5,△ACE≌△DBF,
∴BD=AC=5,
∵BC=2,AC=5,
∴AB=AC﹣BC=5﹣2=3,
∴AD=BD+AB=5+3=8.
11.证明:(1)∵AE⊥BD,CF⊥BD,
∴∠AEB=∠CFD=90°,
∵AB=CD,BE=DF,
∴Rt△ABE≌Rt△CDF(HL);
(2)∵△ABE≌△CDF,
∴∠ABE=∠CDF,
∴AB∥CD,
∵AB=CD,
∴四边形ABCD是平行四边形,
∴AO=CO.
12.证明:∵AE∥BF,
∴∠A=∠FBD(两直线平行,同位角相等),
∵AB=CD,
∴AB+BC=CD+BC(等式的性质),
即AC=BD,
在△ACE与△BDF中,
,
∴△ACE≌△BDF(SAS),
∴∠ECA=∠D(全等三角形的对应角相等),
∴CE∥DF(同位角相等,两直线平行),
故答案为:∠FBD,两直线平行,同位角相等,等式的性质,∠A=∠FBD,SAS,∠ECA=∠D,全等三角形的对应角相等,同位角相等,两直线平行.
13.(1)解:∵∠ABC=45°,∠ADC=60°,
∴∠BAD=∠ADC﹣∠ABC=60°﹣45°=15°,
∵AE⊥BC,
∴∠AEB=90°,
∴△ABE是等腰直角三角形,
∴∠BAE=45°,
∴∠DAE=∠BAE﹣∠BAD=45°﹣15°=30°,
∴∠CAF=∠DAE+∠CAE=30°+15°=45°,
∵CF⊥AD,
∴∠AFC=90°,
∴∠ACF=90°﹣∠CAF=45°;
(2)证明:由(1)可知,∠DAC=45°,∠AFG=∠CFD=90°,∠ACF=∠CAF=45°,
∴AF=CF,
∵AE⊥CB,
∴∠CEG=∠AFG=90°,
∵∠CGE=∠AGF,
∴∠FAG=∠FCD,
在△AFG和△CFD中,
,
∴△AFG≌△CFD(ASA),
∴GF=DF,
由(1)可知,∠FAG=30°,
∵∠AFG=90°,
∴FG=AG,
∴DF=AG.
14.解:(1)四边形ABFE是平行四边形,理由如下:
∵DE∥AB,
∴∠ABO=∠FEO.
∵O是BE中点,
∴OB=OE.
在△AOB和△FOE中,
,
∴△AOB≌△FOE(ASA).
∴AO=FO.
∴四边形ABFE是平行四边形;
(2)∵四边形ABFE是平行四边形,AB=BF,
∴四边形ABFE是菱形,
∴AF⊥BE,
∵AC=10,∠C=30°,
∴OA=5,
∴OC=OA=5.
15.(1)证明:∵CE⊥AB,DF⊥AB,
∴∠AFD=∠BEC=90°,
∵AE=BF,
∴AE+EF=BF+EF,
即AF=BE,
在△ADF和△BCE中,
,
∴△ADF≌△BCE(ASA);
(2)解:∵BC⊥AD,∠A=∠B,
∴∠A=∠B=45°,
∴OA=OB=3,AB=,
∵,
∴,
∴,
∴AD=4,
∴OD=AD﹣OA=4﹣3=1.
16.(1)证明:∵∠BAC=∠DAE,
∴∠BAC﹣∠CAD=∠DAE﹣∠CAD,
即∠BAD=∠CAE,
在△ABD和△ACE中,
,
∴△ABD≌△ACE(SAS),
∴BD=CE;
(2)解:∵AB=AC,AD=AE,∠BAC=∠DAE=α,
∴∠ABC=∠ACB==90°﹣α=∠ADE=∠AED,
由(1)得△ABD≌△ACE,
∴∠ADB=∠AEC=180°﹣∠AED=90°+α,
∴∠DBC=360°﹣∠BCA﹣∠CAD﹣∠ADB
=360°﹣(90°﹣α)﹣(2α﹣β)﹣(90°+α)
=180°﹣2α+β.
17.(1)证明:①在△ABD与△ECB中,
,
∴△ABD≌△ECB(AAS);
②由①得,△ABD≌△ECB,
∴∠ADB=∠EBC,
∴AD∥BC;
(2)解:∵△ABD≌△ECB,
∴BD=BC=15,BE=AD=6,
∴DE=BD﹣BE=15﹣6=9.
18.证明:∵AD∥BE,
∴∠ADC=∠DCE,
∵CD平分∠ACE,
∴∠ACD=∠DCE,
∴∠ACD=∠ADC,
∴AC=AD,
∵AB=AC,
∴AB=AD,
∴∠ABD=∠ADB,
∵AD∥BE,
∴∠ADB=∠DBC,
∴∠ABD=∠DBC,
∵BD平分∠ABC.
19.解:∵∠CPD=20°,∠APB=70°,∠CDP=∠ABP=90°,
∴∠DCP=∠APB=70°.
在△CPD和△PAB中,
,
∴△CPD≌△PAB(ASA).
∴DP=AB.
∵BD=11.2m,BP=3m,
∴DP=BD﹣BP=8.2m,即AB=8.2m.
答:路灯AB的高度是8.2m.
20.(1)证明:在△AOB和△COD中,
,
∴△AOB≌△COD(SAS);
(2)解:由(1)知,△AOB≌△COD,
∴CD=AB=8,
在△BCD中,BC﹣CD<BD<BC+CD,
即2<2OB<18,
∴1<OB<9.
21.解:(1)当t=3时,点P走过的路程为:2×3=6,
∵AB=4,
∴点P运动到线段BC上,
∴BP=6﹣4=2,
故答案为:2;
(2)①当点P在AB上时,△CDP是等腰三角形,
∴PD=CP,
在矩形ABCD中,AD=BC,∠A=∠B=90°,
∴△DAP≌△CBP(HL),
∴AP=BP,
∴AP==2,
∴t==1,
②当点P在BC上时,△CDP是等腰三角形,
∵∠C=90°,
∴CD=CP=4,
∴BP=CB﹣CD=2,
∴t==3,
③当点P在AD上时,△CDP是等腰三角形,
∵∠D=90°,
∴DP=CD=4,
∴t==9,
综上所述,t=1或3或9时,△CDP是等腰三角形;
(3)根据题意,如图,连接CQ,则AB=CD=4,∠A=∠B=∠C=∠D=90o,DQ=5,
∴要使一个三角形与△DCQ全等,则另一条直角边必须等于DQ,
①当点P运动到P1时,CP1=DQ=5,此时△DCQ≌△CDP1,
∴点P的路程为:AB+BP1=4+1=5,
∴t=5÷2=2.5,
②当点P运动到P2时,BP2=DQ=5,此时△CDQ≌△ABP2,
∴点P的路程为:AB+BP2=4+5=9,
∴t=9÷2=4.5,
③当点P运动到P3时,AP3=DQ=5,此时△CDQ≌△ABP3,
∴点P的路程为:AB+BC+CD+DP3=4+6+4+1=15,
∴t=15÷2=7.5,
④当点P运动到P4时,即P与Q重合时,DP4=DQ=5,此时△CDQ≌△CDP4,
∴点P的路程为:AB+BC+CD+DP4=4+6+4+5=19,
∴t=19÷2=9.5,
综上所述,时间的值可以是:t=2.5,4.5,7.5或9.5,
故答案为:2.5或4.5或7.5或9.5.
22.解:(1)由题意得,AP=atcm,BP=(8﹣at)cm,BQ=2tcm,
故答案为:2tcm,(8﹣at)cm;
(2)△BPQ与△CDQ能全等;
∵∠B=∠C,
∴△BPQ与△CDQ全等存在两种情况:
①当△PBQ≌△QCD时,PB=CQ,BQ=CD,
∴2t=6,8﹣at=8﹣2t,
∴a=2,t=3;
②当△PBQ≌△DCQ时,PB=DC,BQ=CQ,
∴8﹣at=6,2t=8﹣2t,
∴a=1,t=2;
综上,△BPQ与△CDQ能全等,此时a=2,t=3或a=1,t=2.
23.解:(1)由题意得:PB=2t,
则PC=6﹣2t;
故答案为:6﹣2t;
(2,理由是:
当t=a=1时,PB=CQ=2,
∴PC=6﹣2=4,
∵∠B=∠C,
∴AC=AB=8,
∵D是AB的中点,
∴BD=AB=4,
∴BD=PC=4,
在△CQP和△BPD中,
,
∴△CQP≌△BPD(SAS);
(3)∵点P、Q的运动速度不相等,
∴PB≠CQ,
当△BPD与△CQP全等,且∠B=∠C,
∴BP=PC=3,CQ=BD=4,
∵BP=2t=3,CQ=at=4,
∴t=,
∴a=4,
∴a=,
∴当a=时,能够使△BPD与△CQP全等,
故答案为:.
24.解:(1)PC=BC﹣BP=(10﹣4t)cm;
故答案为:(10﹣4t);
(2)①若△EBP≌△PCQ
则EB=PC=6,即BP=CQ=4,t=1
得:a=4;
②若△EBP≌△QCP
则EB=CQ=6,BP=CP=5,则t=
得:,
解得:a=.
25.解(1)由题意得:①BD=12,②BP=4t;③CP=16﹣4t,④CQ=at,
(2)∵BP=4t,BD=12,CP=16﹣4t,CQ=at,
∵∠B=∠C,
∴分两种情况:
①若△DBP≌△QCP,
则,
∴,
∴,
②若△DBP≌△PCQ,
则,
∴,
∴.
,综上所述,a的值为6、t的值为2或a的值为4、t的值为1.
故答案为:12,4t,(16﹣4t),at.
26.解:(1)根据题意得t+3t=3+5,
解得t=2,
即t的值为2;
(2)当0≤t≤3时,DM=3﹣t;
当3<t≤8时,DM=t﹣3;
(3)∵ME⊥PQ,NF⊥PQ,
∴∠DEM=∠DFN=90°,
∵∠MDN=90°,
∴∠DME=∠NDF,
∴当DM=DN时,
△DEM与△DFN全等,
当0≤t≤时,3﹣t=5﹣3t,解得t=1,此时DN的长为2;
当<t≤时,3﹣t=3t﹣5,解得t=2,此时DN的长为1,
当<t≤3时,3t﹣5=t﹣3,解得t=1,不合题意舍去;
<t<8时,3=t﹣3,解得t=6,此时DN的长为3.
综上所述,DN的长为1或2或3.
27.解:(1)依题意,得BP=2tcm,
∵BC=10cm,
∴PC=BC﹣BP=(10﹣2t)cm或PC=BP﹣BC=(2t﹣10)cm;
(2)当△CQP是以∠C为顶角的等腰三角形时,CQ=CP,
∴t=10﹣2t或t=2t﹣10,
解得t=或t=10;
(3)∵AD=2BD,AD+DB=AB=18cm,
∴BD=AB=6cm.
如果△BPD与△CQP全等,那么可分两种情况:
①当BP=CQ,BD=CP时,△BPD≌△CQP,
∴2t=at,10﹣2t=6,
∴t=2,a=2;
②当BP=CP,BD=CQ时,△BPD≌△CPQ,
∵BP+CP=BC=10cm,
∴BP=CP=BC=5cm,
∵2t=5,解得t=2.5,
∵at=6,
∴2.5a=6,
解得:a=2.4,
综上所述:当点Q的运动速度为2或2.4cm/s时,能使△BPD与△CQP全等.
解答题专题提升训练(附答案)
1.如图,C、E分别在AB、DF上,O是CF的中点,EO=BO,求证:∠ACE+∠DEC=180°.
证明:∵O是CF的中点,
∴ = ,
在△COB和△FOE中,
.
∴△COB≌△FOE ( ),
∴∠ =∠ ,( ).
∴AB∥DF,( ).
∴∠ACE+∠DEC=180°.( ).
2.如图,在四边形ABCD中,AD∥BC,点E为对角线BD上一点,∠A=∠BEC,且AD=BE.
(1)求证:△ABD≌△ECB;
(2)若∠BDC=70°,求∠DBC的度数.
3.如图,在△ABC中,点D在AC上,BD平分∠ABC,延长BA到点E,使得BE=BC,连接DE,若∠ADE=38°,∠C=42°,求∠BAD的度数.
4.如图所示,点E在△ABC外部,点D在BC边上,DE交AC于F,若∠1=∠3,∠E=∠C,AE=AC,问△ABC≌△ADE吗?请说明理由.
5.如图,△AOB≌△COD,OD与AB交于点G,OB与CD交于点E.
(1)∠AOD与∠COB的数量关系是:∠AOD ∠COB;
(2)求证:△AOG≌△COE;
(3)若OA=OB,当A,O,C三点共线时,恰好OB⊥CD,则此时∠AOB= °.
6.△ABC和△ADE如图所示,其中∠ABC=∠ACB,∠ADE=∠AED,∠BAC=∠DAE.
(1)如图①,连接BE、CD,求证:BE=CD;
(2)如图②,连接BE、CD、BD,若∠BAC=∠DAE=60°,CD⊥AE,AD=3,CD=5,求BD的长.
7.如图,点C、E、F、B在同一直线上,点A、D在BC异侧,AB∥CD,AB=CD,BF=CE.
(1)试说明:∠A=∠D;
(2)若AB=CF,∠A比∠B的余角大20°,求∠D的度数.
8.如图,Rt△ACB中,∠ACB=90°,∠CAB与∠ABC的角平分线BE,AD相交于点G,过G作AD垂线交BC的延长线于点F,交AC于点H.
(1)求∠DGB的大小;
(2)若AD=10,GF=6,求GH长度;
(3)若S△ABG=5,求四边形ABDE的面积.
9.如图,在△ABC中,AD⊥BC,CE⊥AB,垂足分别为D,E,AD与CE相交于点F,且AE=CD.
(1)求证:AB=CB;
(2)若DF=3,CD=4,求点F到AC的距离.
10.如图,点A、B、C、D在同一条直线上,△ACE≌△DBF,已知AC=5,BC=2,求AD的长.
11.如图,在四边形ABCD中,AB=CD,E、F是对角线BD上两点,且BE=DF,AE⊥BD,CF⊥BD,垂足分别是E、F.
(1)求证:△ABE≌△CDF;
(2)若AC与BD交于点O,求证:OA=OC.
12.如图,A、B、C、D在同一直线上,AB=CD,AE∥BF,AE=BF.请将证明“CE∥DF”推理过程补充完整.
证明:∵AE∥BF,∴∠A= ( )
∵AB=CD,
∴AB+BC=CD+BC( )
即AC=BD
在△ACE与△BDF中
∴△ACE≌△BDF( )
∴ ( )
∴CE∥DF( )
13.如图,△ABC中,∠ABC=45°,D为BC上一点,∠ADC=60°,AE⊥BC于点E,CF⊥AD于点F,AE、CF相交于点G,∠CAE=15°.
(1)求∠ACF的度数;
(2)求证:DF=AG.
14.如图,点D为△ABC边AC上一点,过点D作DE∥AB,点O为BE的中点,连接AO并延长,交DE的延长线于点F,连接AE、BF.
(1)试判断四边形ABFE的形状,并说明理由;
(2)若AB=BF,AC=10,∠C=30°,求OC的长.
15.如图,A,E,F,B在同一条直线上,CE⊥AB,DF⊥AB,垂足分别为E,F,AE=BF,∠A=∠B.
(1)求证:△ADF≌△BCE.
(2)当BC⊥AD时,,OA=3时,求OD的长.
16.已知AB=AC,AD=AE,∠BAC=∠DAE.
(1)如图1,当点D在BC上时,求证:BD=CE;
(2)如图2,当点D、E、C在同一直线上,且∠BAC=α,∠BAE=β时,求∠DBC的度数(用含α和β的式子表示).
17.如图,在四边形ABCD中,点E为对角线BD上一点,∠A=∠BEC,∠ABD=∠BCE,且AD=BE.
(1)证明:①△ABD≌△ECB;②AD∥BC;
(2)若BC=15,AD=6,请求出DE的长度.
18.如图,已知点A、C分别在∠GBE的边BG、BE上,且AB=AC,AD∥BE,与∠ACE的平分线CD交于点D,连接BD.求证:BD平分∠ABC.
19.小明利用一根长3 m的竿子来测量路灯AB的高度.他的方法如下:如图,在路灯前选一点P,使BP=3m,并测得∠APB=70°,然后把竖直的竿子CD(CD=3m)在BP的延长线上左右移动,使∠CPD=20°,此时测得BD=11.2m.请根据这些数据,计算出路灯AB的高度.
20.已知AC、BD相交于点O,OA=OC,OB=OD.
(1)求证:△AOB≌△COD;
(2)连接BC,若AB=8,BC=10,求OB的取值范围.
21.如图,长方形ABCD中,AB=4cm,BC=6cm,现有一动点P从A出发以2cm/秒的速度,沿矩形的边A﹣B﹣C﹣D﹣A返回到点A停止,设点P运动的时间为t秒.
(1)当t=3时,BP= cm;
(2)当t为何值时,连接CP,DP,△CDP是等腰三角形;
(3)Q为AD边上的点,且DQ=5,当t为何值时,以长方形的两个顶点及点P为顶点的三角形与△DCQ全等.
22.如图,已知四边形ABCD中,AB=BC=8cm,CD=6cm,∠B=∠C,动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速运动,点Q运动的速度是每秒2cm,点P运动的速度是每秒acm(a≤2),当点Q到达点C时,P、Q两点都停止运动,设运动时间为t秒.
(1)BQ= ,BP= .(用含a或t的代数式表示)
(2)运动过程中,连接PQ,DQ,△BPQ与△CDQ能否全等?若能,请求出相应的t和a的值,若不能,说明理由.
23.如图,已知△ABC中,∠B=∠C,AB=8,BC=6,点D为AB的中点,如果点P在线段BC上以每秒2个单位长度的速度由B点向C点运动,同时,点Q在线段CA上以每秒a个单位长度的速度由C点向A点运动,设运动时间为t(秒)(0≤t≤3)
(1)PC= (用含t的代数式表示);
(2)若点P、Q的运动速度相等,经过1秒后,△BPD与△CQP是否全等,请说明理由;
(3)若点P、Q的运动速度不相等,当点Q的运动速度a= 时,能够使△BPD与△CQP全等.
24.已知正方形ABCD中,边长为10cm,点E在AB边上,BE=6cm,如果点P在线段BC上以4cm/s的速度由点B向点C运动,同时点Q在线段CD上以acm/的速度由点C向点D运动,设运动的时间为t秒,
(1)CP的长为 cm(用含t的代数式表示)
(2)若以E、B、P为顶点的三角形和以P、C、Q为顶点的三角形全等,求a的值
25.如图,已知△ABC中,AB=AC=24厘米,∠ABC=∠ACB,BC=16厘米,点D为AB的中点.如果点P在线段BC上以4厘米/秒的速度由B点向C点运动.同时,点Q在线段CA上由C点以a厘米/秒的速度向A点运动.设运动的时间为t秒.
(1)直接写出:
①BD= 厘米; ②BP= 厘米;
③CP= 厘米; ④CQ= 厘米;
(可用含t、a的代数式表示)
(2)若以D,B,P为顶点的三角形和以P,C,Q为顶点的三角形全等,试求a、t的值.
26.如图,在矩形ABCD中,AD=3,DC=5,动点M从A点出发沿线段AD﹣DC以每秒1个单位长度的速度向终点C运动;动点N同时从C点出发沿线段CD﹣DA以每秒3个单位长度的速度向终点A运动.ME⊥PQ于点E,NF⊥PQ于点F,设运动的时间为t秒.
(1)在运动过程中当M、N两点相遇时,求t的值.
(2)在整个运动过程中,求DM的长.(用含t的代数式表示)
(3)当△DEM与△DFN全等时,请直接写出所有满足条件的DN的长.
27.如图,在△ABC中,AB=AC=18cm,BC=10cm,AD=2BD.动点P以2cm/s的速度沿射线BC运动,同时,点Q从点C出发,以acm/s的速度向终点A运动,当Q点停止运动时,P点也随之停止运动,设点P的运动时间为t(s)(t>0).
(1)用含t的代数式表示PC的长;
(2)若点Q的运动速度为1cm/s,当△CQP是以∠C为顶角的等腰三角形时,求t的值;
(3)当点Q的运动速度为多少时,能使△BPD与△CQP在某一时刻全等.
参考答案
1.证明:∵O是CF的中点,
∴CO=FO,
在△COB和△FOE中,
,
∴△COB≌△FOE(SAS),
∴∠OBC=∠OEF(全等三角形对应角相等),
∴AB∥DF(内错角相等,两直线平行),
∴∠ACE+∠DEC=180°(两直线平行,同旁内角互补).
故答案为:CO;FO;SAS;OBC;OEF;全等三角形对应角相等;内错角相等,两直线平行;两直线平行,同旁内角互补.
2.(1)证明:∵AD∥BC,
∴∠ADB=∠EBC,
在△ABD和△ECB中,
,
∴△ABD≌△ECB(ASA);
(2)解:∵△ABD≌△ECB,
∴BD=BC,
∴∠BDC=∠BCD=70°,
∴∠DBC=40°.
3.解:∵BD平分∠ABC,
∴∠EBD=∠CBD,
在△BDE和△BDC中,
,
∴△BDE≌△BDC(SAS),
∴∠E=∠C=42°,
∵∠ADE=38°,
∴∠BAD=∠ADE+∠E=38°+42°=80°.
4.解:△ABC和△ADE全等,
理由是:∵∠ADC=∠B+∠1=∠3+∠ADE,
又∵∠1=∠3,
∴∠B=∠ADE,
在△ABC和△ADE中,
,
∴△ABC≌△ADE(AAS),
即△ABC和△ADE全等.
5.(1)解:∵△AOB≌△COD,
∴∠AOB=∠COD,
∴∠AOB﹣∠BOD=∠COD﹣∠BOD,
即∠AOD=∠COB,
故答案为:=;
(2)证明:∵△AOB≌△COD,
∴OA=OC,∠A=∠C,
在△AOG和△COE中,
,
∴△AOG≌△COE(ASA);
(3)如图,∵△AOB≌△COD,
∴OA=OC,OB=OD,
∵OA=OB,
∴OA=OB=OC=OD,
∵OB⊥CD,
∴CE=DE,
∴OE是△ACD的中位线,
∴OE∥AD,
∴∠ODA=∠BOD,
∵OA=OD,
∴∠OAD=∠ODA,
∵∠OAD+∠ODA+∠AOD=∠BOD+∠BOC+∠AOD=180°,∠AOD=∠BOC,
∴∠AOD=∠BOD=∠BOC=60°,
∴∠AOB=120°,
故答案为:120.
6.(1)证明:∵∠ABC=∠ACB,∠ADE=∠AED,CAD
∴AB=AC,AE=AD,
∵,∠BAC=∠DAE,
∴∠BAE=∠CAD,
∴△ABE≌△ACD(SAS),
∴BE=CD.
(2)解:∵∠ADE=∠AED,
∴AE=AD,
∵∠DAE=60°,
∴△DAE是等边三角形,
∴AD=ED=3,∠AED=∠ADE=60°,
∵CD⊥AE,
∴∠ADC=×60°=30°,
由(1)知:△ABE≌△ACD,
∴BE=CD=5,∠AEB=∠ADC=30°,
∴∠BED=90°,
∴BD=.
7.解:(1)∵AB∥CD,
∴∠C=∠B,
∵CE=BF,
∴CE+EF=FB+EF,
即CF=BE,
在△AEB和△DFC中,
,
∴△AEB≌△DFC(SAS),
∴∠A=∠D;
(2)设∠B=x,则∠B的余角为90°﹣x,
∵∠A比∠B的余角大20°,
∴∠A=90°﹣x+20°=110°﹣x,
∵BE=CF,AB=CF,
∴AB=BE,
∴∠AEB=∠A=110°﹣x,
由三角形内角和为180°得:2(110°﹣x)+x=180°,
解得:x=40°,
∴∠D=∠A=110°﹣40°=70°.
8.解:(1)∵△ABC的角平分线AD、BE相交于点G,
∴∠GAB+∠GBA=(∠CAB+∠CBA)=45°,
∴∠DGB=∠GAB+∠ABG=45°;
(2)∵∠ACB=90°,
∴∠FCH=90°,
由(1)知:∠DGB=45°,
∴∠AGB=135°,
又∵GF⊥AD,
∴∠FGB=90°+45°=135°,
∴∠AGB=∠FGB,
∵∠AHG=∠CHF,∠AGH=∠FCH=90°,
∴∠BFH=∠CAD=∠BAD,
在△ABG和△FBG中,
,
∴△ABG≌△FBG(ASA),
∴GA=GF,
∵AD=10,GF=6,
∴DG=AD﹣AG=AD﹣FG=10﹣6=4,
∵∠F=∠CAD,∠AGH=∠FGD,AG=FG,
∴△AGH≌△FGD(AAS),
∴GH=DG=4;
(3)如图,
∵△ABG≌△FBG,△AGH≌△FGD,
∴S△AGB=S△FBG,S△AGH=S△FGD,GH=GD,
∵∠HGD=90°,
∴∠HDG=∠DHG=45°=∠BGD,
∴HD∥EG,
∴S△EGH=S△EGD,
∵S四边形ABDE=S△ABG+S△AEG+S△EGD+S△GBD=S△ABG+(S△AEG+S△EGH)+S△GBD
=S△ABG+S△FGD+S△GBD
=S△ABG+S△FBG
=2S△ABG
=2×5
=10.
9.证明:(1)∵AD⊥BC,CE⊥AB,
∴∠AEF=∠CDF=∠BEC=∠BDA=90°.
在△AEF和△CDF中,
∴△AEF≌△CDF(AAS),
∴EF=DF,AF=CF.
∴EF+CF=DF+AF,
∴EC=DA,
在△ABD和△CBE中,
∴△ABD≌△CBE(AAS),
∴AB=CB;
(2)∵△AEF≌△CDF,
∴AF=CF,
∵DF=3,CD=4,
∴在Rt△CDF中,CF=5,
∴AD=AF+DF=CF+DF=5+3=8,
在Rt△ADC中,AC=,
设点F到AC的距离为h,
∵,
∴,
∴点F到AC的距离为.
10.解:∵AC=5,△ACE≌△DBF,
∴BD=AC=5,
∵BC=2,AC=5,
∴AB=AC﹣BC=5﹣2=3,
∴AD=BD+AB=5+3=8.
11.证明:(1)∵AE⊥BD,CF⊥BD,
∴∠AEB=∠CFD=90°,
∵AB=CD,BE=DF,
∴Rt△ABE≌Rt△CDF(HL);
(2)∵△ABE≌△CDF,
∴∠ABE=∠CDF,
∴AB∥CD,
∵AB=CD,
∴四边形ABCD是平行四边形,
∴AO=CO.
12.证明:∵AE∥BF,
∴∠A=∠FBD(两直线平行,同位角相等),
∵AB=CD,
∴AB+BC=CD+BC(等式的性质),
即AC=BD,
在△ACE与△BDF中,
,
∴△ACE≌△BDF(SAS),
∴∠ECA=∠D(全等三角形的对应角相等),
∴CE∥DF(同位角相等,两直线平行),
故答案为:∠FBD,两直线平行,同位角相等,等式的性质,∠A=∠FBD,SAS,∠ECA=∠D,全等三角形的对应角相等,同位角相等,两直线平行.
13.(1)解:∵∠ABC=45°,∠ADC=60°,
∴∠BAD=∠ADC﹣∠ABC=60°﹣45°=15°,
∵AE⊥BC,
∴∠AEB=90°,
∴△ABE是等腰直角三角形,
∴∠BAE=45°,
∴∠DAE=∠BAE﹣∠BAD=45°﹣15°=30°,
∴∠CAF=∠DAE+∠CAE=30°+15°=45°,
∵CF⊥AD,
∴∠AFC=90°,
∴∠ACF=90°﹣∠CAF=45°;
(2)证明:由(1)可知,∠DAC=45°,∠AFG=∠CFD=90°,∠ACF=∠CAF=45°,
∴AF=CF,
∵AE⊥CB,
∴∠CEG=∠AFG=90°,
∵∠CGE=∠AGF,
∴∠FAG=∠FCD,
在△AFG和△CFD中,
,
∴△AFG≌△CFD(ASA),
∴GF=DF,
由(1)可知,∠FAG=30°,
∵∠AFG=90°,
∴FG=AG,
∴DF=AG.
14.解:(1)四边形ABFE是平行四边形,理由如下:
∵DE∥AB,
∴∠ABO=∠FEO.
∵O是BE中点,
∴OB=OE.
在△AOB和△FOE中,
,
∴△AOB≌△FOE(ASA).
∴AO=FO.
∴四边形ABFE是平行四边形;
(2)∵四边形ABFE是平行四边形,AB=BF,
∴四边形ABFE是菱形,
∴AF⊥BE,
∵AC=10,∠C=30°,
∴OA=5,
∴OC=OA=5.
15.(1)证明:∵CE⊥AB,DF⊥AB,
∴∠AFD=∠BEC=90°,
∵AE=BF,
∴AE+EF=BF+EF,
即AF=BE,
在△ADF和△BCE中,
,
∴△ADF≌△BCE(ASA);
(2)解:∵BC⊥AD,∠A=∠B,
∴∠A=∠B=45°,
∴OA=OB=3,AB=,
∵,
∴,
∴,
∴AD=4,
∴OD=AD﹣OA=4﹣3=1.
16.(1)证明:∵∠BAC=∠DAE,
∴∠BAC﹣∠CAD=∠DAE﹣∠CAD,
即∠BAD=∠CAE,
在△ABD和△ACE中,
,
∴△ABD≌△ACE(SAS),
∴BD=CE;
(2)解:∵AB=AC,AD=AE,∠BAC=∠DAE=α,
∴∠ABC=∠ACB==90°﹣α=∠ADE=∠AED,
由(1)得△ABD≌△ACE,
∴∠ADB=∠AEC=180°﹣∠AED=90°+α,
∴∠DBC=360°﹣∠BCA﹣∠CAD﹣∠ADB
=360°﹣(90°﹣α)﹣(2α﹣β)﹣(90°+α)
=180°﹣2α+β.
17.(1)证明:①在△ABD与△ECB中,
,
∴△ABD≌△ECB(AAS);
②由①得,△ABD≌△ECB,
∴∠ADB=∠EBC,
∴AD∥BC;
(2)解:∵△ABD≌△ECB,
∴BD=BC=15,BE=AD=6,
∴DE=BD﹣BE=15﹣6=9.
18.证明:∵AD∥BE,
∴∠ADC=∠DCE,
∵CD平分∠ACE,
∴∠ACD=∠DCE,
∴∠ACD=∠ADC,
∴AC=AD,
∵AB=AC,
∴AB=AD,
∴∠ABD=∠ADB,
∵AD∥BE,
∴∠ADB=∠DBC,
∴∠ABD=∠DBC,
∵BD平分∠ABC.
19.解:∵∠CPD=20°,∠APB=70°,∠CDP=∠ABP=90°,
∴∠DCP=∠APB=70°.
在△CPD和△PAB中,
,
∴△CPD≌△PAB(ASA).
∴DP=AB.
∵BD=11.2m,BP=3m,
∴DP=BD﹣BP=8.2m,即AB=8.2m.
答:路灯AB的高度是8.2m.
20.(1)证明:在△AOB和△COD中,
,
∴△AOB≌△COD(SAS);
(2)解:由(1)知,△AOB≌△COD,
∴CD=AB=8,
在△BCD中,BC﹣CD<BD<BC+CD,
即2<2OB<18,
∴1<OB<9.
21.解:(1)当t=3时,点P走过的路程为:2×3=6,
∵AB=4,
∴点P运动到线段BC上,
∴BP=6﹣4=2,
故答案为:2;
(2)①当点P在AB上时,△CDP是等腰三角形,
∴PD=CP,
在矩形ABCD中,AD=BC,∠A=∠B=90°,
∴△DAP≌△CBP(HL),
∴AP=BP,
∴AP==2,
∴t==1,
②当点P在BC上时,△CDP是等腰三角形,
∵∠C=90°,
∴CD=CP=4,
∴BP=CB﹣CD=2,
∴t==3,
③当点P在AD上时,△CDP是等腰三角形,
∵∠D=90°,
∴DP=CD=4,
∴t==9,
综上所述,t=1或3或9时,△CDP是等腰三角形;
(3)根据题意,如图,连接CQ,则AB=CD=4,∠A=∠B=∠C=∠D=90o,DQ=5,
∴要使一个三角形与△DCQ全等,则另一条直角边必须等于DQ,
①当点P运动到P1时,CP1=DQ=5,此时△DCQ≌△CDP1,
∴点P的路程为:AB+BP1=4+1=5,
∴t=5÷2=2.5,
②当点P运动到P2时,BP2=DQ=5,此时△CDQ≌△ABP2,
∴点P的路程为:AB+BP2=4+5=9,
∴t=9÷2=4.5,
③当点P运动到P3时,AP3=DQ=5,此时△CDQ≌△ABP3,
∴点P的路程为:AB+BC+CD+DP3=4+6+4+1=15,
∴t=15÷2=7.5,
④当点P运动到P4时,即P与Q重合时,DP4=DQ=5,此时△CDQ≌△CDP4,
∴点P的路程为:AB+BC+CD+DP4=4+6+4+5=19,
∴t=19÷2=9.5,
综上所述,时间的值可以是:t=2.5,4.5,7.5或9.5,
故答案为:2.5或4.5或7.5或9.5.
22.解:(1)由题意得,AP=atcm,BP=(8﹣at)cm,BQ=2tcm,
故答案为:2tcm,(8﹣at)cm;
(2)△BPQ与△CDQ能全等;
∵∠B=∠C,
∴△BPQ与△CDQ全等存在两种情况:
①当△PBQ≌△QCD时,PB=CQ,BQ=CD,
∴2t=6,8﹣at=8﹣2t,
∴a=2,t=3;
②当△PBQ≌△DCQ时,PB=DC,BQ=CQ,
∴8﹣at=6,2t=8﹣2t,
∴a=1,t=2;
综上,△BPQ与△CDQ能全等,此时a=2,t=3或a=1,t=2.
23.解:(1)由题意得:PB=2t,
则PC=6﹣2t;
故答案为:6﹣2t;
(2,理由是:
当t=a=1时,PB=CQ=2,
∴PC=6﹣2=4,
∵∠B=∠C,
∴AC=AB=8,
∵D是AB的中点,
∴BD=AB=4,
∴BD=PC=4,
在△CQP和△BPD中,
,
∴△CQP≌△BPD(SAS);
(3)∵点P、Q的运动速度不相等,
∴PB≠CQ,
当△BPD与△CQP全等,且∠B=∠C,
∴BP=PC=3,CQ=BD=4,
∵BP=2t=3,CQ=at=4,
∴t=,
∴a=4,
∴a=,
∴当a=时,能够使△BPD与△CQP全等,
故答案为:.
24.解:(1)PC=BC﹣BP=(10﹣4t)cm;
故答案为:(10﹣4t);
(2)①若△EBP≌△PCQ
则EB=PC=6,即BP=CQ=4,t=1
得:a=4;
②若△EBP≌△QCP
则EB=CQ=6,BP=CP=5,则t=
得:,
解得:a=.
25.解(1)由题意得:①BD=12,②BP=4t;③CP=16﹣4t,④CQ=at,
(2)∵BP=4t,BD=12,CP=16﹣4t,CQ=at,
∵∠B=∠C,
∴分两种情况:
①若△DBP≌△QCP,
则,
∴,
∴,
②若△DBP≌△PCQ,
则,
∴,
∴.
,综上所述,a的值为6、t的值为2或a的值为4、t的值为1.
故答案为:12,4t,(16﹣4t),at.
26.解:(1)根据题意得t+3t=3+5,
解得t=2,
即t的值为2;
(2)当0≤t≤3时,DM=3﹣t;
当3<t≤8时,DM=t﹣3;
(3)∵ME⊥PQ,NF⊥PQ,
∴∠DEM=∠DFN=90°,
∵∠MDN=90°,
∴∠DME=∠NDF,
∴当DM=DN时,
△DEM与△DFN全等,
当0≤t≤时,3﹣t=5﹣3t,解得t=1,此时DN的长为2;
当<t≤时,3﹣t=3t﹣5,解得t=2,此时DN的长为1,
当<t≤3时,3t﹣5=t﹣3,解得t=1,不合题意舍去;
<t<8时,3=t﹣3,解得t=6,此时DN的长为3.
综上所述,DN的长为1或2或3.
27.解:(1)依题意,得BP=2tcm,
∵BC=10cm,
∴PC=BC﹣BP=(10﹣2t)cm或PC=BP﹣BC=(2t﹣10)cm;
(2)当△CQP是以∠C为顶角的等腰三角形时,CQ=CP,
∴t=10﹣2t或t=2t﹣10,
解得t=或t=10;
(3)∵AD=2BD,AD+DB=AB=18cm,
∴BD=AB=6cm.
如果△BPD与△CQP全等,那么可分两种情况:
①当BP=CQ,BD=CP时,△BPD≌△CQP,
∴2t=at,10﹣2t=6,
∴t=2,a=2;
②当BP=CP,BD=CQ时,△BPD≌△CPQ,
∵BP+CP=BC=10cm,
∴BP=CP=BC=5cm,
∵2t=5,解得t=2.5,
∵at=6,
∴2.5a=6,
解得:a=2.4,
综上所述:当点Q的运动速度为2或2.4cm/s时,能使△BPD与△CQP全等.
