2022-2023学年青岛版八年级数学上册2.6等腰三角形(2)课件(共23张PPT)
文档属性
| 名称 | 2022-2023学年青岛版八年级数学上册2.6等腰三角形(2)课件(共23张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 298.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-09 00:00:00 | ||
图片预览








文档简介
(共23张PPT)
温馨提示:
1.请同学们打开课本第57页,准备好课本、练习册、双色笔、尺规、 作业本.
2.端正坐好、精神饱满,准备上课.
3.背诵:
等腰三角形的性质
试一试,你能行!拼一拼,你能赢!
我们在上一节学习了等腰三角形的性质。你还能回答出来吗?
等腰三角形的性质:
1.等腰三角形是轴对称图形.等腰三角形的对称轴是底边的垂直平分线.
2.等腰三角形的底边上的高、 底边上的中线、顶角的平分线重合(也称三线合一)。
3.等腰三角形的两个底角相等。(等边对等角)
等腰三角形的两个底角相等。
(可以简称:等边对等角)
这个定理的条件和结论交换一下是什么?
如果一个三角形有两个角相等,
那么这个三角形是等腰三角形。
3、这个命题正确吗?你能证明吗?
§2.6等腰三角形(2)
学习目标
1.掌握等腰三角形的判定方法;
2.会运用等腰三角形的判定方法判断一个三角形
是否为等腰三角形。
学习指导(一)
请同学们用6分钟的时间,认真学习课本第57页—第58页的内容,并解决以下问题:
1.动手实验,你探究到的等腰三角形的判定是什么?
2.例3、例4是如何利用等腰三角形的判定解题的?
6分钟后比一比,看谁是记忆达人!解题高手!
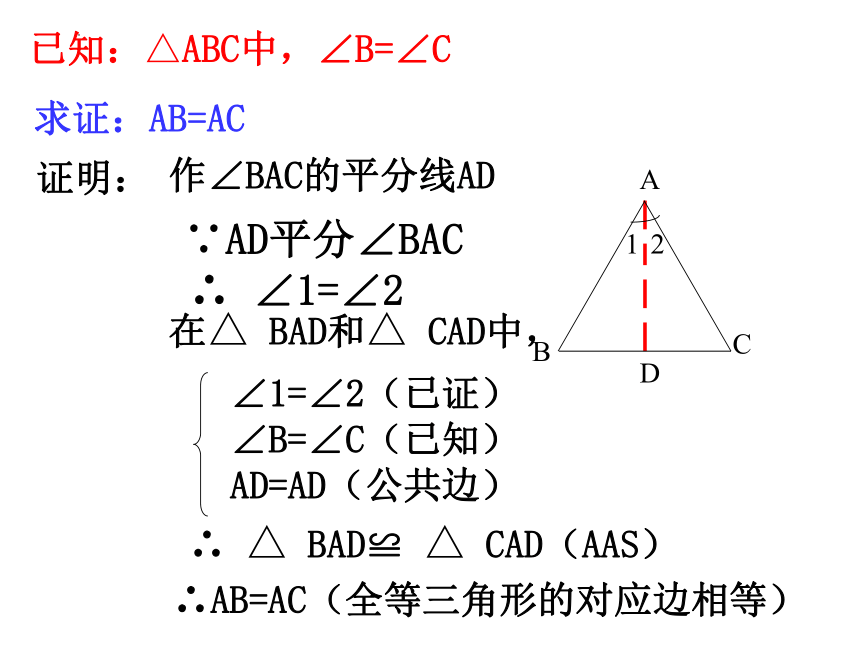
已知:△ABC中,∠B=∠C
求证:AB=AC
证明:
作∠BAC的平分线AD
在△ BAD和△ CAD中,
∠1=∠2(已证)
∠B=∠C(已知)
AD=AD(公共边)
∴ △ BAD≌ △ CAD(AAS)
∴AB=AC(全等三角形的对应边相等)
1
A
B
C
D
2
∵AD平分∠BAC
∴ ∠1=∠2
注意:使用“等角对等边”前提是---在同一个三角形中
等腰三角形的判定:
如果一个三角形有两个角相等,那么这两个角所对的边也相等(简写成“等角对等边”).
练习1
B
A
D
C
已知:如图,
AD ∥BC,BD平分∠ABC。
求证:AB=AD
解答
B
A
D
C
证明: ∵ AD ∥BC
∴∠ADB=∠DBC(两直线平行,内错角相等)
∵ BD平分∠ABC ∴∠ABD=∠DBC
∵∠ADB=∠DBC
∴∠ABD=∠ADB
∴AB=AD
例3:
C
B
A
D
1
2
已知:如图, ∠A=∠DBC =360, ∠C=720。计算∠1和∠2,并说明图中有哪些等腰三角形?
解:
∠1=720
∠2=360
等腰三角形有:△ABC,△ ABD,△ BCD
C
B
A
D
1
2
课本:P59 第1题做到书上!
1.等腰三角形有:
△ABC,△ ABD,△ ADE,△ AEC
例4: 如图,在ABC中,AB=AC, 与 是的平分线交于点F, 是等腰三角形吗?为什么?
练习3
解答
2.如图,把一张长方形形的纸沿对角线折叠.重合部分是一个等腰三角形吗?为什么?
A
B
C
D
E
F
解答
答案:是等腰三角形.
因为,如图可证∠1=∠2.
A
B
E
D
C
F
1、这节课你学会了哪些知识?
2、通过这节课的学习,你有什么体会?
畅所欲言
我的收获
等腰三角形的判定:
如果一个三角形有两个角相等,那么这两个角所对的边也相等(简写成“等角对等边”).
挑战自我
解:
作业
课本第59页 练习 2题
练习册P19 1---- 5.
比一比!看谁做的又对又快!
堂清检测
课后记:
1.等腰三角形的判定,是一个判定同一个三角形中两线段相等的方法;
2.对于要证两个三角形中的线段相等,一般通过证明这两条线段所在的三角形全等。
温馨提示:
1.请同学们打开课本第57页,准备好课本、练习册、双色笔、尺规、 作业本.
2.端正坐好、精神饱满,准备上课.
3.背诵:
等腰三角形的性质
试一试,你能行!拼一拼,你能赢!
我们在上一节学习了等腰三角形的性质。你还能回答出来吗?
等腰三角形的性质:
1.等腰三角形是轴对称图形.等腰三角形的对称轴是底边的垂直平分线.
2.等腰三角形的底边上的高、 底边上的中线、顶角的平分线重合(也称三线合一)。
3.等腰三角形的两个底角相等。(等边对等角)
等腰三角形的两个底角相等。
(可以简称:等边对等角)
这个定理的条件和结论交换一下是什么?
如果一个三角形有两个角相等,
那么这个三角形是等腰三角形。
3、这个命题正确吗?你能证明吗?
§2.6等腰三角形(2)
学习目标
1.掌握等腰三角形的判定方法;
2.会运用等腰三角形的判定方法判断一个三角形
是否为等腰三角形。
学习指导(一)
请同学们用6分钟的时间,认真学习课本第57页—第58页的内容,并解决以下问题:
1.动手实验,你探究到的等腰三角形的判定是什么?
2.例3、例4是如何利用等腰三角形的判定解题的?
6分钟后比一比,看谁是记忆达人!解题高手!
已知:△ABC中,∠B=∠C
求证:AB=AC
证明:
作∠BAC的平分线AD
在△ BAD和△ CAD中,
∠1=∠2(已证)
∠B=∠C(已知)
AD=AD(公共边)
∴ △ BAD≌ △ CAD(AAS)
∴AB=AC(全等三角形的对应边相等)
1
A
B
C
D
2
∵AD平分∠BAC
∴ ∠1=∠2
注意:使用“等角对等边”前提是---在同一个三角形中
等腰三角形的判定:
如果一个三角形有两个角相等,那么这两个角所对的边也相等(简写成“等角对等边”).
练习1
B
A
D
C
已知:如图,
AD ∥BC,BD平分∠ABC。
求证:AB=AD
解答
B
A
D
C
证明: ∵ AD ∥BC
∴∠ADB=∠DBC(两直线平行,内错角相等)
∵ BD平分∠ABC ∴∠ABD=∠DBC
∵∠ADB=∠DBC
∴∠ABD=∠ADB
∴AB=AD
例3:
C
B
A
D
1
2
已知:如图, ∠A=∠DBC =360, ∠C=720。计算∠1和∠2,并说明图中有哪些等腰三角形?
解:
∠1=720
∠2=360
等腰三角形有:△ABC,△ ABD,△ BCD
C
B
A
D
1
2
课本:P59 第1题做到书上!
1.等腰三角形有:
△ABC,△ ABD,△ ADE,△ AEC
例4: 如图,在ABC中,AB=AC, 与 是的平分线交于点F, 是等腰三角形吗?为什么?
练习3
解答
2.如图,把一张长方形形的纸沿对角线折叠.重合部分是一个等腰三角形吗?为什么?
A
B
C
D
E
F
解答
答案:是等腰三角形.
因为,如图可证∠1=∠2.
A
B
E
D
C
F
1、这节课你学会了哪些知识?
2、通过这节课的学习,你有什么体会?
畅所欲言
我的收获
等腰三角形的判定:
如果一个三角形有两个角相等,那么这两个角所对的边也相等(简写成“等角对等边”).
挑战自我
解:
作业
课本第59页 练习 2题
练习册P19 1---- 5.
比一比!看谁做的又对又快!
堂清检测
课后记:
1.等腰三角形的判定,是一个判定同一个三角形中两线段相等的方法;
2.对于要证两个三角形中的线段相等,一般通过证明这两条线段所在的三角形全等。
同课章节目录
- 第1章 全等三角形
- 1.1 全等三角形
- 1.2 怎样判定三角形全等
- 1.3 尺规作图
- 第2章 图形的轴对称
- 2.1 图形的轴对称
- 2.2 轴对称的基本性质
- 2.3 轴对称图形
- 2.4 线段的垂直平分线
- 2.5 角平分线的性质
- 2.6 等腰三角形
- 第3章 分式
- 3.1 分式的基本性质
- 3.2 分式的约分
- 3.3 分式的乘法与除法
- 3.4 分式的通分
- 3.5 分式的加法与减法
- 3.6 比和比例
- 3.7 可化为一元一次方程的分式方程
- 第4章 数据分析
- 4.1 加权平均数
- 4.2 中位数
- 4.3 众数
- 4.4 数据的离散程度
- 4.5 方差
- 4.6 用计算器计算平均数和方差
- 第5章 几何证明初步
- 5.1 定义与命题
- 5.2 为什么要证明
- 5.3 什么是几何证明
- 5.4 平行线的性质定理和判定定理
- 5.5 三角形内角和定理
- 5.6 几何证明举例
