2022-2023学年青岛版八年级数学上册2.5角平分线的性质(1)课件(共17张PPT)
文档属性
| 名称 | 2022-2023学年青岛版八年级数学上册2.5角平分线的性质(1)课件(共17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 231.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-09 00:00:00 | ||
图片预览





文档简介
(共17张PPT)
课前准备
1. 打开课本P51、准备好:练习册、练习本、作业本、双色笔、作图工具.
2.知识回顾:
(1)角平分线的定义和点到直线的距离的定义;
(2)线段的垂直平分线的性质、判定.
课堂大舞台 人人展风采!
§2.5角平分线的性质
学习目标
1.能够通过折纸、画图等操作,体会角的对称性,
而认识角平分线的性质;
2.能够用尺规作图,作出角的平分线;
3.会用角的平分线解答简单的计算和证明.
学习指导
时间:6分钟
内容:课本第51页—第53页
任务:1.通过动手实验你探究到的角的对称性、角
平分线的性质分别是什么?
2.你会用尺规作出一个角的平分线吗?
比一比!试着说出角的对称性、角平分线的性质! 作图高手:会用尺规作出已知角的平分线.
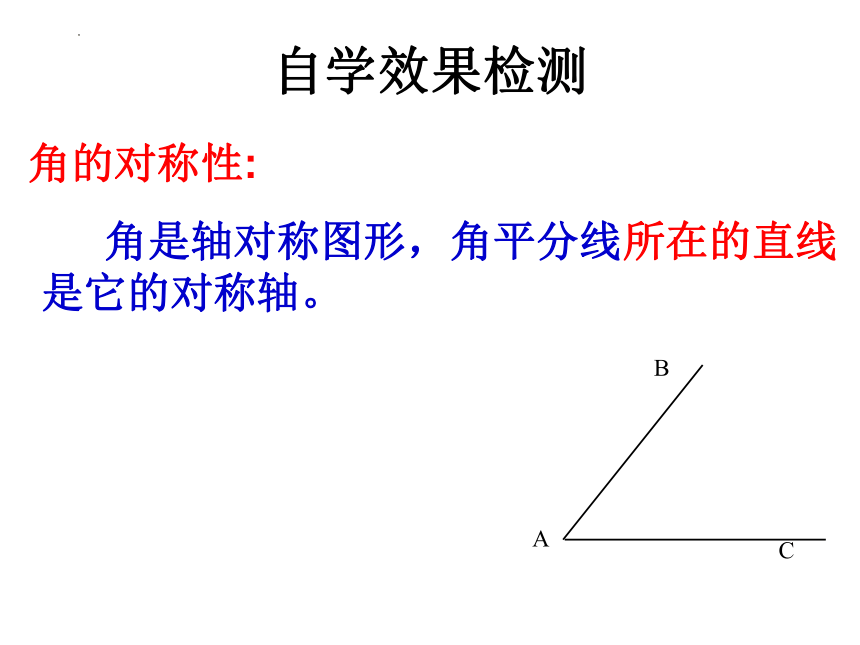
自学效果检测
角是轴对称图形,角平分线所在的直线是它的对称轴。
B
A
C
角的对称性:
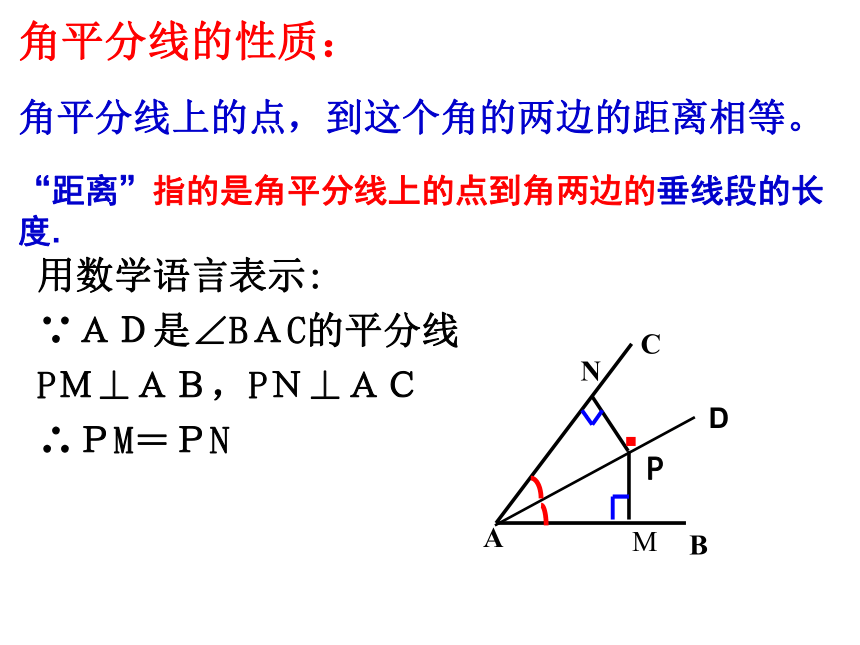
角平分线上的点,到这个角的两边的距离相等。
用数学语言表示:
∵AD是∠BAC的平分线
PM⊥AB,PN⊥AC
∴PM=PN
N
P
M
C
A
B
D
“距离”指的是角平分线上的点到角两边的垂线段的长度.
角平分线的性质:
.
角平分线的判定:
角的内部到角的两边距离相等的点在这个角的平分线上。
如图用数学语言表示
∵PM⊥AB,PN⊥AC
PM=PN
N
P
M
C
A
B
D
∴点P在∠BAC的平分线上
已知一个角,你能用直尺和圆规作出这个角的平分线吗?
A
B
O
M
N
C
射线OC即为所求.
已知:∠AOB
求作: ∠AOB的平分线OC
请把课本P53练习 1、2 题做到书上
实战演练:
1、这节课你学会了哪些知识?
2、通过这节课的学习,你有什么体会?
畅所欲言
1.角平分线上的点,到这个角的两边的距离相等。
2.角的内部到角的两边距离相等的点在这个角的平分线上。
3.用尺规作出个一个角的平分线
我的收获
,
1、在Rt△ABC中,BD是角平分线,DE⊥AB,垂足为E,DE与DC相等吗?为什么?
A
B
C
D
E
2、如图,OC是∠AOB的平分线,点P在OC上,PD ⊥OA,PE⊥OB,垂足分别是D、E,PD=4cm,则PE=__________cm.
A
D
O
B
E
P
C
堂清检测
相等(角平分线上的点,到这个角的两边的距离相等。)
4
3.已知△ABC中, ∠C=900,AD平分∠ CAB,且 BC=8,BD=5,求点D到AB的距离是多少?
E
A
B
C
D
你会吗?
3
3
练习册P17 1---- 6.
比一比!看谁做的又对又快!
堂清检测
作业
课本第53页习题2.5 1.
1.通过让学生动手实验探究角的对称性、角平
分线的性质,调动了学生学习的积极性。
2.对课堂所用时间把握不够准确,由于在开始 的尺规作图中浪费了一部分时间,以至于在后面所准备的习题没有时间去练习。
课后记
课前准备
1. 打开课本P51、准备好:练习册、练习本、作业本、双色笔、作图工具.
2.知识回顾:
(1)角平分线的定义和点到直线的距离的定义;
(2)线段的垂直平分线的性质、判定.
课堂大舞台 人人展风采!
§2.5角平分线的性质
学习目标
1.能够通过折纸、画图等操作,体会角的对称性,
而认识角平分线的性质;
2.能够用尺规作图,作出角的平分线;
3.会用角的平分线解答简单的计算和证明.
学习指导
时间:6分钟
内容:课本第51页—第53页
任务:1.通过动手实验你探究到的角的对称性、角
平分线的性质分别是什么?
2.你会用尺规作出一个角的平分线吗?
比一比!试着说出角的对称性、角平分线的性质! 作图高手:会用尺规作出已知角的平分线.
自学效果检测
角是轴对称图形,角平分线所在的直线是它的对称轴。
B
A
C
角的对称性:
角平分线上的点,到这个角的两边的距离相等。
用数学语言表示:
∵AD是∠BAC的平分线
PM⊥AB,PN⊥AC
∴PM=PN
N
P
M
C
A
B
D
“距离”指的是角平分线上的点到角两边的垂线段的长度.
角平分线的性质:
.
角平分线的判定:
角的内部到角的两边距离相等的点在这个角的平分线上。
如图用数学语言表示
∵PM⊥AB,PN⊥AC
PM=PN
N
P
M
C
A
B
D
∴点P在∠BAC的平分线上
已知一个角,你能用直尺和圆规作出这个角的平分线吗?
A
B
O
M
N
C
射线OC即为所求.
已知:∠AOB
求作: ∠AOB的平分线OC
请把课本P53练习 1、2 题做到书上
实战演练:
1、这节课你学会了哪些知识?
2、通过这节课的学习,你有什么体会?
畅所欲言
1.角平分线上的点,到这个角的两边的距离相等。
2.角的内部到角的两边距离相等的点在这个角的平分线上。
3.用尺规作出个一个角的平分线
我的收获
,
1、在Rt△ABC中,BD是角平分线,DE⊥AB,垂足为E,DE与DC相等吗?为什么?
A
B
C
D
E
2、如图,OC是∠AOB的平分线,点P在OC上,PD ⊥OA,PE⊥OB,垂足分别是D、E,PD=4cm,则PE=__________cm.
A
D
O
B
E
P
C
堂清检测
相等(角平分线上的点,到这个角的两边的距离相等。)
4
3.已知△ABC中, ∠C=900,AD平分∠ CAB,且 BC=8,BD=5,求点D到AB的距离是多少?
E
A
B
C
D
你会吗?
3
3
练习册P17 1---- 6.
比一比!看谁做的又对又快!
堂清检测
作业
课本第53页习题2.5 1.
1.通过让学生动手实验探究角的对称性、角平
分线的性质,调动了学生学习的积极性。
2.对课堂所用时间把握不够准确,由于在开始 的尺规作图中浪费了一部分时间,以至于在后面所准备的习题没有时间去练习。
课后记
同课章节目录
- 第1章 全等三角形
- 1.1 全等三角形
- 1.2 怎样判定三角形全等
- 1.3 尺规作图
- 第2章 图形的轴对称
- 2.1 图形的轴对称
- 2.2 轴对称的基本性质
- 2.3 轴对称图形
- 2.4 线段的垂直平分线
- 2.5 角平分线的性质
- 2.6 等腰三角形
- 第3章 分式
- 3.1 分式的基本性质
- 3.2 分式的约分
- 3.3 分式的乘法与除法
- 3.4 分式的通分
- 3.5 分式的加法与减法
- 3.6 比和比例
- 3.7 可化为一元一次方程的分式方程
- 第4章 数据分析
- 4.1 加权平均数
- 4.2 中位数
- 4.3 众数
- 4.4 数据的离散程度
- 4.5 方差
- 4.6 用计算器计算平均数和方差
- 第5章 几何证明初步
- 5.1 定义与命题
- 5.2 为什么要证明
- 5.3 什么是几何证明
- 5.4 平行线的性质定理和判定定理
- 5.5 三角形内角和定理
- 5.6 几何证明举例
