2022—2023学年青岛版数学八年级上册2.6等腰三角形(3)课件(共17张PPT)
文档属性
| 名称 | 2022—2023学年青岛版数学八年级上册2.6等腰三角形(3)课件(共17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 234.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-09 16:42:30 | ||
图片预览




文档简介
(共17张PPT)
复习回顾
等腰三角形的性质
1.等腰三角形是轴对称图形.等腰三角形的对称轴是底边的垂直平分线.
2.等腰三角形的底边上的高、底边上的中线及顶角的平分线重合.
3. 等腰三角形的两个底角相等.
等边三角形的定义:
三条边都相等的三角形是等边三角形.
青岛版 八年级上册 第二章
2.6 等腰三角形(3)
学习目标
1.掌握等边三角形的性质以及等边三角形的
判定方法.
2.正确运用等边三角形的性质以及等边三角
形的判定方法解决有关问题.
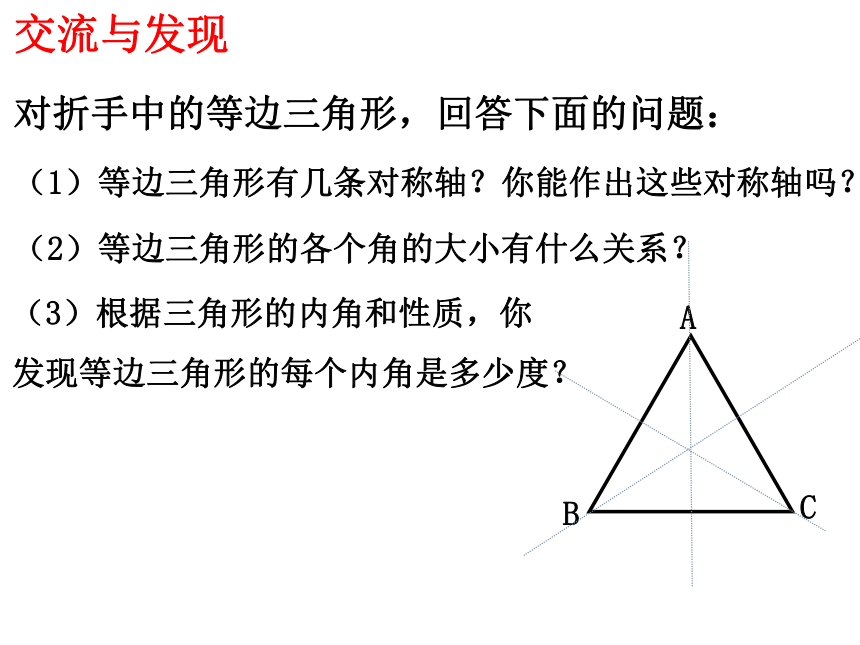
交流与发现
对折手中的等边三角形,回答下面的问题:
(1)等边三角形有几条对称轴?你能作出这些对称轴吗?
(2)等边三角形的各个角的大小有什么关系?
A
B
C
(3)根据三角形的内角和性质,你 发现等边三角形的每个内角是多少度?
A
B
C
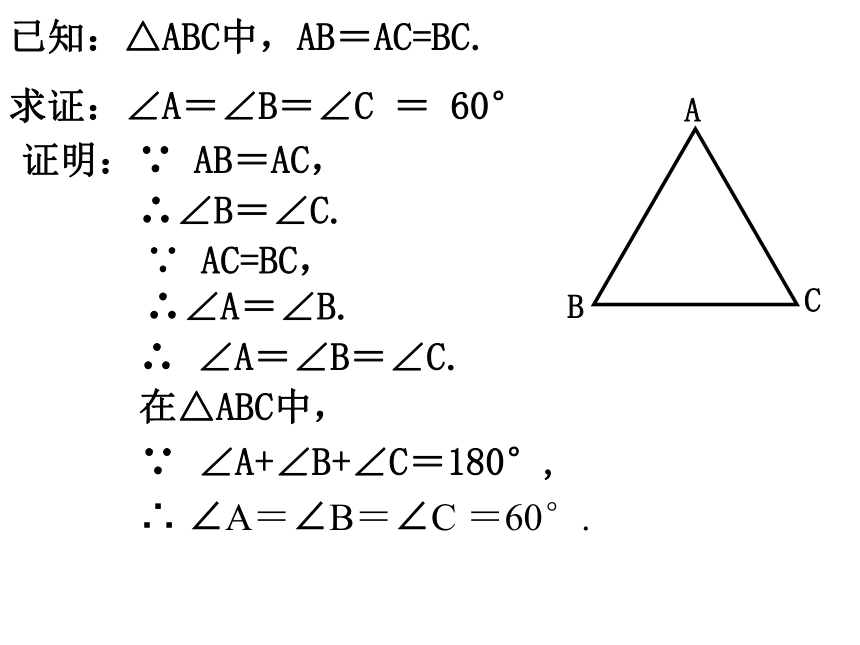
证明:∵ AB=AC,
∴∠B=∠C.
在△ABC中,
∵ ∠A+∠B+∠C=180°,
∴ ∠A=∠B=∠C =60°.
∵ AC=BC,
∴∠A=∠B.
∴ ∠A=∠B=∠C.
已知:△ABC中,AB=AC=BC.
求证:∠A=∠B=∠C = 60°
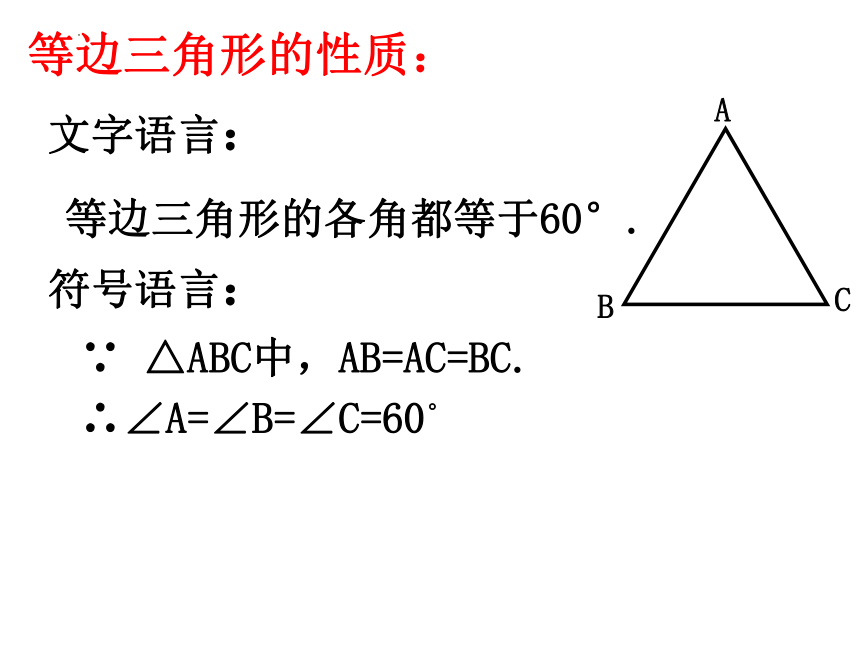
等边三角形的性质:
等边三角形的各角都等于60°.
∵ △ABC中,AB=AC=BC.
文字语言:
∴∠A=∠B=∠C=60。
A
B
C
符号语言:
练一练:
如图,在等边△ABC中,BC=10,BD⊥AC于D,
则∠ABD= . AD= .
30°
5
(4)如果一个三角形的三个角都相等,这个三角形是等边三角形吗?说明你的理由,并与同学交流
交流与发现
C
A
B
已知:△ABC中,∠A=∠B=∠C.
求证:△ABC是等边三角形.
证明:∵∠A=∠B,
∴AC=BC.
∵∠B=∠C,
∴AC=AB.
∴AC=AB=BC.
即△ABC是等边三角形.
符号语言:
在△ABC 中,
∵ ∠A=∠B =∠C ,
∴ △ABC 是等边三角形.
等边三角形的判定:
文字语言:
三个角都相等的三角形是等边三角形.
C
A
B
(5)有一个内角为60°的等腰三角形 是等边三角形吗?
交流与发现
C
A
B
①
已知:
△ABC中,AB=AC,∠B=60°
求证:△ABC是等边三角形
证明:
∵AB=AC,∠B=60°
∴∠C=∠B=60°
∵∠A=180°-(∠B+∠C)=60°
于是∠A=∠B=∠C
∴△ABC是等边三角形
②
已知:
△ABC中,AB=AC,∠A=60°
求证:△ABC是等边三角形
证明:
∵AB=AC,∠A=60°
∠A+∠B+∠C=180°
∴∠C=∠B=60°
于是∠A=∠B=∠C
∴△ABC是等边三角形
分类讨论思想
由①②可知,有一个内角为60°的等腰三角形是等边三角形
等边三角形的判定方法:
C
A
B
有一个内角为60°的等腰三角形是等边三角形.
)
60°
P
A
B
练一练:
课外活动小组在一次测量活动中,测得∠APB=60°AP=BP=2m,他们便得到了一个结论:池塘的长为 .
2 m
课堂小结
1.等边三角形的性质.
2.等边三角形的判定.
A
C
B
P
Q
1200
3
1
2
1.如图,P、Q是△ABC的边BC上的两点,并且BP=PQ=AP=AQ=CQ,∠BAC= .
堂清检测
堂清检测
2.下面的判断中,错误的是( )
(A)在△ABC中,如果AB=AC,且∠A=∠B,那么△ABC为等边三角形.
(B)在△ABC中,如果AB=AC,且∠B=∠C,那么△ABC为等边三角形.
(C)在△ABC中,如果∠A=60°,且∠B=60°,那么△ABC为等边三角形.
(D)在△ABC中,如果AB=AC,且∠B=60°,那么△ABC为等边三角形.
B
3.如图,△ABC是等边三角形,AD为中线,AD=AE,E在AC上,求∠EDC的度数.
堂清检测
解:
∵△ABC是等边三角形,AD为中线
∴AD⊥BC
∴∠CAD= ∠BAC=30°
∵ AD=AE
∴∠ADE=∠AED= (180°-∠CAD)=75°
∴∠EDC=∠ADC-∠ADE=90°-75°=15°
作业
课本第62页习题2.6 第4题
复习回顾
等腰三角形的性质
1.等腰三角形是轴对称图形.等腰三角形的对称轴是底边的垂直平分线.
2.等腰三角形的底边上的高、底边上的中线及顶角的平分线重合.
3. 等腰三角形的两个底角相等.
等边三角形的定义:
三条边都相等的三角形是等边三角形.
青岛版 八年级上册 第二章
2.6 等腰三角形(3)
学习目标
1.掌握等边三角形的性质以及等边三角形的
判定方法.
2.正确运用等边三角形的性质以及等边三角
形的判定方法解决有关问题.
交流与发现
对折手中的等边三角形,回答下面的问题:
(1)等边三角形有几条对称轴?你能作出这些对称轴吗?
(2)等边三角形的各个角的大小有什么关系?
A
B
C
(3)根据三角形的内角和性质,你 发现等边三角形的每个内角是多少度?
A
B
C
证明:∵ AB=AC,
∴∠B=∠C.
在△ABC中,
∵ ∠A+∠B+∠C=180°,
∴ ∠A=∠B=∠C =60°.
∵ AC=BC,
∴∠A=∠B.
∴ ∠A=∠B=∠C.
已知:△ABC中,AB=AC=BC.
求证:∠A=∠B=∠C = 60°
等边三角形的性质:
等边三角形的各角都等于60°.
∵ △ABC中,AB=AC=BC.
文字语言:
∴∠A=∠B=∠C=60。
A
B
C
符号语言:
练一练:
如图,在等边△ABC中,BC=10,BD⊥AC于D,
则∠ABD= . AD= .
30°
5
(4)如果一个三角形的三个角都相等,这个三角形是等边三角形吗?说明你的理由,并与同学交流
交流与发现
C
A
B
已知:△ABC中,∠A=∠B=∠C.
求证:△ABC是等边三角形.
证明:∵∠A=∠B,
∴AC=BC.
∵∠B=∠C,
∴AC=AB.
∴AC=AB=BC.
即△ABC是等边三角形.
符号语言:
在△ABC 中,
∵ ∠A=∠B =∠C ,
∴ △ABC 是等边三角形.
等边三角形的判定:
文字语言:
三个角都相等的三角形是等边三角形.
C
A
B
(5)有一个内角为60°的等腰三角形 是等边三角形吗?
交流与发现
C
A
B
①
已知:
△ABC中,AB=AC,∠B=60°
求证:△ABC是等边三角形
证明:
∵AB=AC,∠B=60°
∴∠C=∠B=60°
∵∠A=180°-(∠B+∠C)=60°
于是∠A=∠B=∠C
∴△ABC是等边三角形
②
已知:
△ABC中,AB=AC,∠A=60°
求证:△ABC是等边三角形
证明:
∵AB=AC,∠A=60°
∠A+∠B+∠C=180°
∴∠C=∠B=60°
于是∠A=∠B=∠C
∴△ABC是等边三角形
分类讨论思想
由①②可知,有一个内角为60°的等腰三角形是等边三角形
等边三角形的判定方法:
C
A
B
有一个内角为60°的等腰三角形是等边三角形.
)
60°
P
A
B
练一练:
课外活动小组在一次测量活动中,测得∠APB=60°AP=BP=2m,他们便得到了一个结论:池塘的长为 .
2 m
课堂小结
1.等边三角形的性质.
2.等边三角形的判定.
A
C
B
P
Q
1200
3
1
2
1.如图,P、Q是△ABC的边BC上的两点,并且BP=PQ=AP=AQ=CQ,∠BAC= .
堂清检测
堂清检测
2.下面的判断中,错误的是( )
(A)在△ABC中,如果AB=AC,且∠A=∠B,那么△ABC为等边三角形.
(B)在△ABC中,如果AB=AC,且∠B=∠C,那么△ABC为等边三角形.
(C)在△ABC中,如果∠A=60°,且∠B=60°,那么△ABC为等边三角形.
(D)在△ABC中,如果AB=AC,且∠B=60°,那么△ABC为等边三角形.
B
3.如图,△ABC是等边三角形,AD为中线,AD=AE,E在AC上,求∠EDC的度数.
堂清检测
解:
∵△ABC是等边三角形,AD为中线
∴AD⊥BC
∴∠CAD= ∠BAC=30°
∵ AD=AE
∴∠ADE=∠AED= (180°-∠CAD)=75°
∴∠EDC=∠ADC-∠ADE=90°-75°=15°
作业
课本第62页习题2.6 第4题
同课章节目录
- 第1章 全等三角形
- 1.1 全等三角形
- 1.2 怎样判定三角形全等
- 1.3 尺规作图
- 第2章 图形的轴对称
- 2.1 图形的轴对称
- 2.2 轴对称的基本性质
- 2.3 轴对称图形
- 2.4 线段的垂直平分线
- 2.5 角平分线的性质
- 2.6 等腰三角形
- 第3章 分式
- 3.1 分式的基本性质
- 3.2 分式的约分
- 3.3 分式的乘法与除法
- 3.4 分式的通分
- 3.5 分式的加法与减法
- 3.6 比和比例
- 3.7 可化为一元一次方程的分式方程
- 第4章 数据分析
- 4.1 加权平均数
- 4.2 中位数
- 4.3 众数
- 4.4 数据的离散程度
- 4.5 方差
- 4.6 用计算器计算平均数和方差
- 第5章 几何证明初步
- 5.1 定义与命题
- 5.2 为什么要证明
- 5.3 什么是几何证明
- 5.4 平行线的性质定理和判定定理
- 5.5 三角形内角和定理
- 5.6 几何证明举例
