第4章圆复习课件

课件30张PPT。圆的复习学习目标：
1、系统熟悉圆的有关概念。
2、巩固有关圆的一些性质和定理。
3、进一步掌握应用圆的有关知识解决某些数学问题。学习要求：
1、圆是如何定义的？
2、同圆或等圆中的弧、弦、圆心角有什么关系？垂直于弦的直径有什么性质？一条弧所对的圆周角和它所对的圆心角有什么关系？
3、点和圆有怎样的位置关系？直线和圆呢？圆和圆呢？怎样判断这些位置关系呢？
4、圆的切线有什么性质？如何判断一条直线是圆的切线？
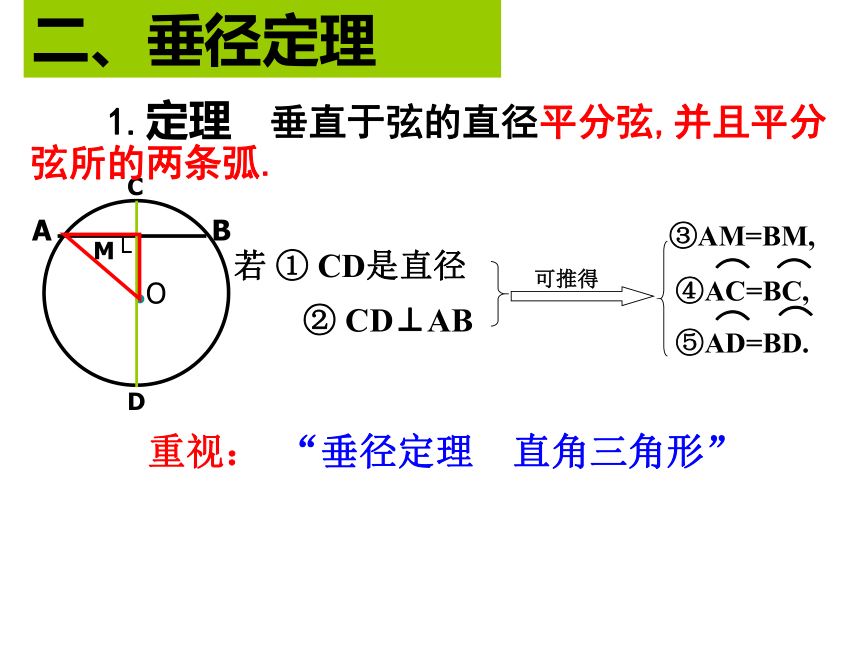
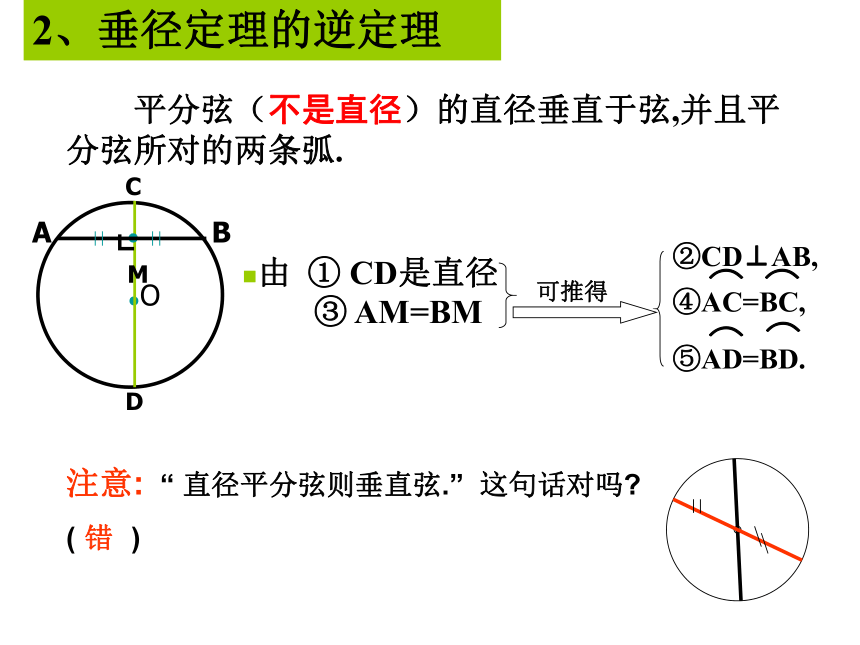
5、如何计算弧长、扇形面积？(1)弦是直径；(2)半圆是弧；(3)过圆心的线段是直径；(7)圆心相同，半径相等的两个圆是同心圆;(8)半径相等的两个圆是等圆.(4)过圆心的直线是直径；(5)半圆是最长的弧；(6)直径是最长的弦；判断：一、圆的基本概念二、垂径定理③AM=BM,重视： “垂径定理 直角三角形” 若 ① CD是直径② CD⊥AB　　1.定理 垂直于弦的直径平分弦,并且平分弦所的两条弧.　　平分弦（不是直径）的直径垂直于弦,并且平 分弦所对的两条弧.注意: “ 直径平分弦则垂直弦.” 这句话对吗?
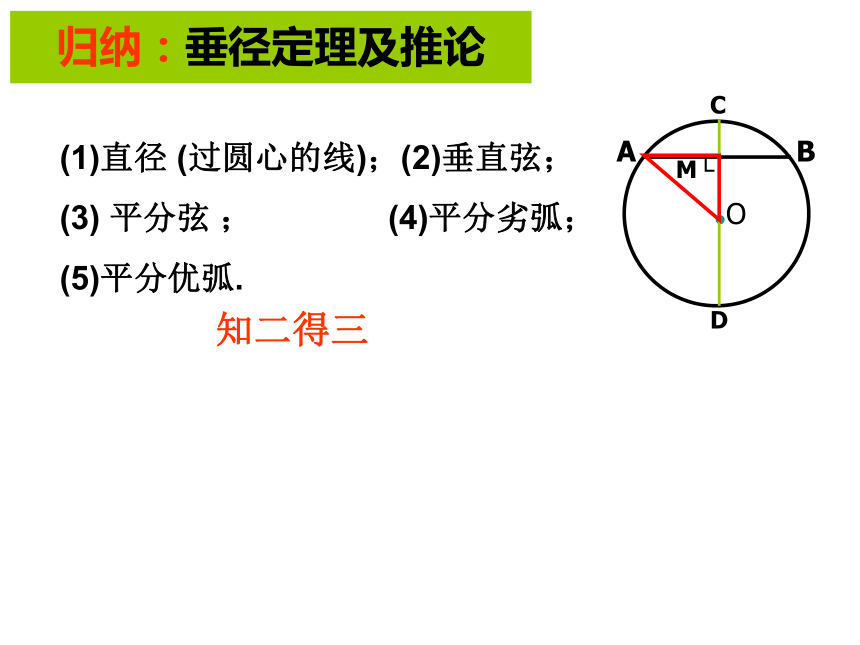
( )错2、垂径定理的逆定理直径 (过圆心的线)；(2)垂直弦；
(3) 平分弦 ；　　　　(4)平分劣弧；
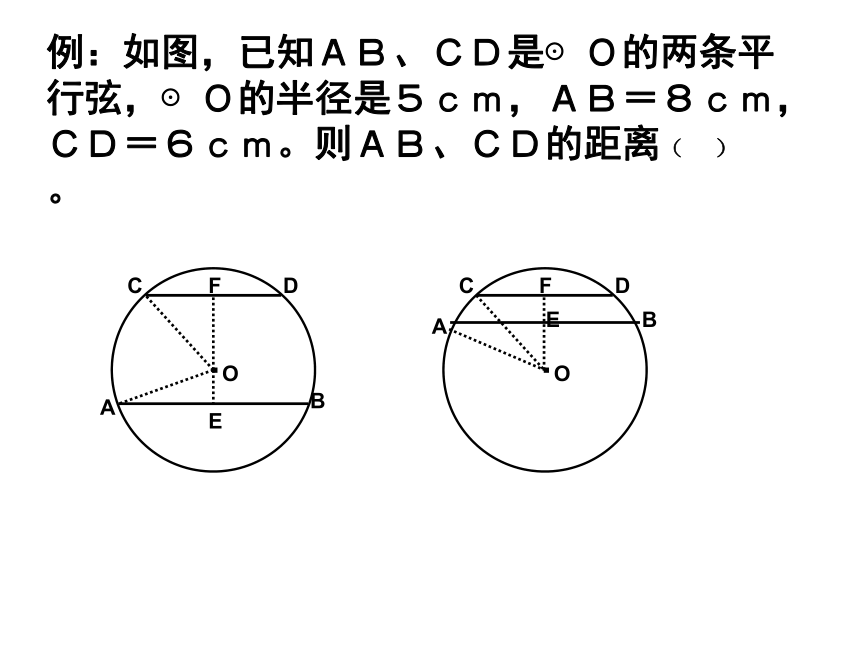
(5)平分优弧.知二得三归纳：垂径定理及推论例：如图，已知ＡＢ、ＣＤ是⊙Ｏ的两条平行弦，⊙Ｏ的半径是５ｃｍ，ＡＢ＝８ｃｍ，ＣＤ＝６ｃｍ。则ＡＢ、ＣＤ的距离（ ）
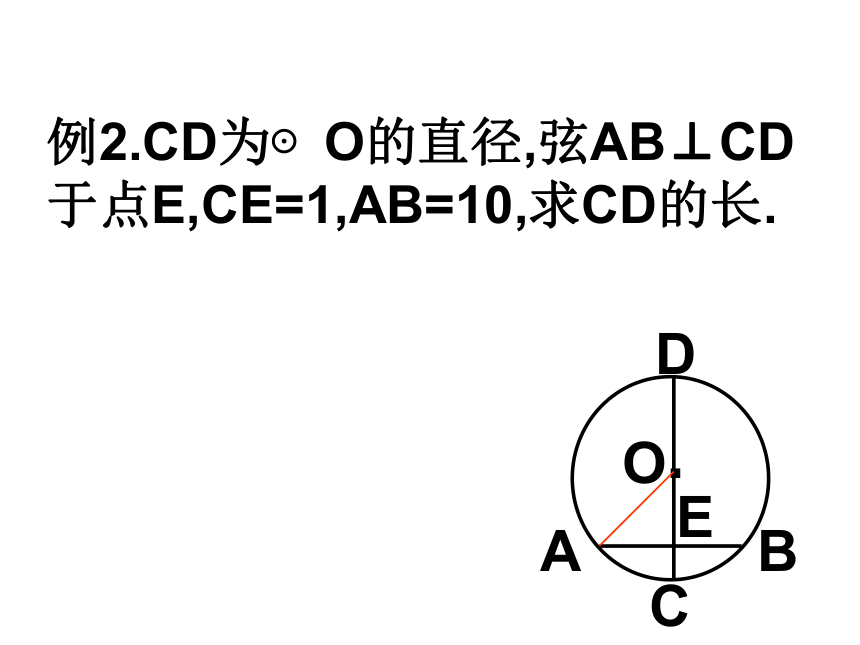
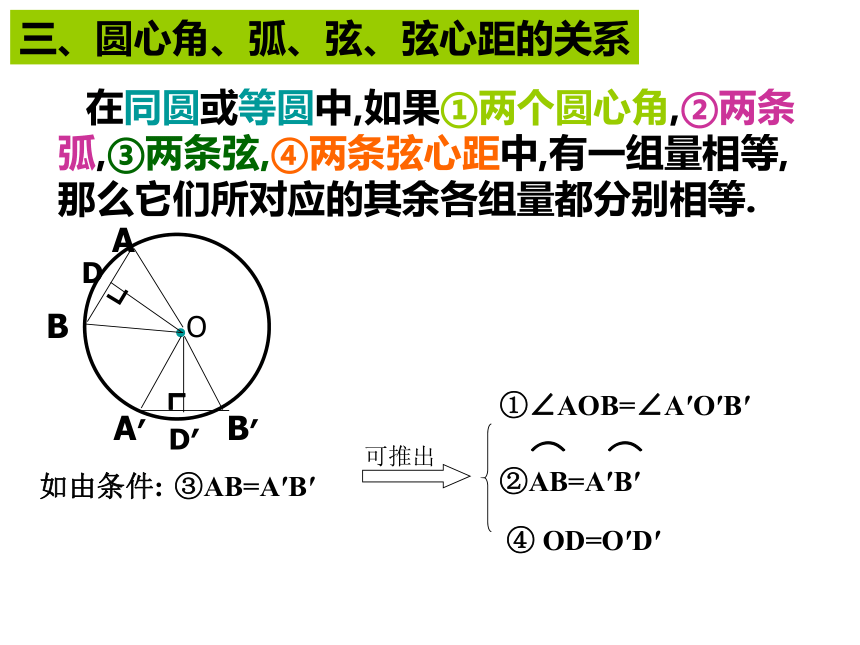
。例2.CD为⊙O的直径,弦AB⊥CD于点E,CE=1,AB=10,求CD的长.ABCDEO.如由条件:③AB=A′B′④ OD=O′D′①∠AOB=∠A′O′B′三、圆心角、弧、弦、弦心距的关系 在同圆或等圆中,如果①两个圆心角,②两条弧,③两条弦,④两条弦心距中,有一组量相等,那么它们所对应的其余各组量都分别相等.四、圆周角定理及推论 90°的圆周角所对的弦是 . 定理:一条弧所对的圆周角的度数都等于这弧所对的圆心角度数的一半.
在同圆或等圆中,同弧或等弧所对的圆周角相等。
推论:直径所对的圆周角是 .直角直径判断: (1) 相等的圆心角所对的弧相等.
(2)相等的圆周角所对的弧相等.
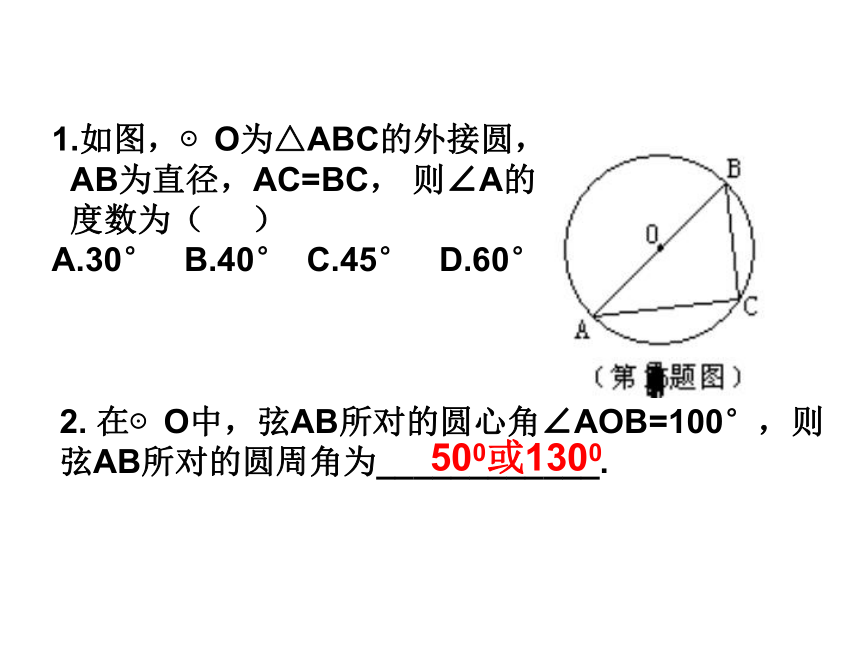
(3) 等弧所对的圆周角相等.(×)(×)(√)2. 在⊙O中，弦AB所对的圆心角∠AOB=100°，则弦AB所对的圆周角为____________.1.如图，⊙O为△ABC的外接圆，
AB为直径，AC=BC， 则∠A的
度数为（ ）
A.30° B.40° C.45° D.60°500或1300五、点和圆的位置关系d r;d r;2、直线和圆相切3、直线和圆相离d r.<=>1、直线和圆相交六.直线与圆的位置关系(1)当 r 满足______时，⊙C与直线AB相离。例：在Rt△ABC中，∠C=90°，AC=3cm， BC=4cm，以C为圆心，r为半径作圆。d=2.4cmBCAD453看谁做得快、做得好！2.4cm或4cm等于2.4大于2.4小于2.4CD●OA　如图
　
　∵OA是⊙O的半径, 且CD⊥OA,
　∴ CD是⊙O的切线.七、切线的判定定理定理 经过半径的外端,并且垂直于这
条半径的直线是圆的切线.例：（2009?黔东南州）如图，△ABC中，AB=AC，O是BC的中点，以O为 圆心的圆与AB相切于点D，求证：AC是圆的切线
　　　　　　　　　　　　　小组讨论：判定切线连半径，证垂直，作垂直，证半径连接OD，作OE垂直与AC.E
　∵CD切⊙O于Ａ, OA是⊙O的半径CD●OA∴CD⊥OA.切线的性质圆的切线垂直于过切点的直径ABCO八.三角形的外接圆和内切圆：ABCI三角形内切圆的圆心叫三角形的内心。三角形外接圆的圆心叫三角形的外心三角形三边垂直平分线的交点三角形三内角角平分线的交点到三角形各边的距离相等到三角形各顶点的距离相等锐角三角形的外心位于三角形内,
直角三角形的外心位于直角三角形斜边中点,
钝角三角形的外心位于三角形外.三角形的外心是否一定在三角形的内部？例.已知△ABC，AC=12，BC=5，AB=13。则△ABC的外接圆半径为 。(04年广东)交点个数 名称0外离1外切2相交1内切0内含同心圆是内含的特殊情况d , R , r 的关系dR rd > R + rd = R + rR-r< d < R+ rd = R - r0≤ d < R - r九.圆与圆的位置关系例．已知两圆的半径分别是2和3，两圆的圆心距
是4，则这两个圆的位置关系是 （ ）
A．外离 B．外切 C．相交 D． 内切 Ｃ1.圆的周长和面积公式2.弧长的计算公式3.扇形的面积公式或四.圆中的有关计算:周长C=2πr面积s=πr21、 如图,当半径为30cm的转动轮转过120°时,传送带上的物体A平移的距离为______.20πcm当堂达标　　
1、 如图1，⊙O中弧AB的度数为60°，AC是⊙O的直
径，那么∠BOC等于 ( )；
　A．150° B．130° C．120° D．60°
2、如图2，AB是⊙O的直径，C为圆上一点，弧AC度数为60°，OD⊥BC，D为垂足，且OD=10，则AB=_____，BC=_____；
3、在△ABC中，∠A＝70°，若O为△ABC的外心，∠BOC= 　；若O为△ABC的内心，∠BOC= 　．
　　　　　　　　　　　　图1　　　　　　　　　　　　　图2
　4、为改善市区人民生活环境，市建设污水管网工程，某圆柱型水管的直径为100 cm，截面如图2，若管内污水的面宽AB=60 cm，则污水的最大深度为 cm；
　 　　　　　　　　　　　图1　　　　　　　　　　　5、⊙O的半径为R，圆心到点A的距离为d，且R、d分别是方程x2－6x＋8＝0的两根，则点A与⊙O的位置关系是（ ）
A．点A在⊙O内部 B．点A在⊙O上
C．点A在⊙O外部 D．点A不在⊙O上
　　
9.如图，AB是⊙O的直径，弦CD⊥AB，垂足为E，如果AB=26，CD=24，那么sin∠OCE=　　 ．
解析：如图：
∵AB为⊙0直径，AB=26，
∴OC=×26=13，
又∵CD⊥AB，
∴CE=CD=12，
在Rt△OCE中，OE===5，
∴sin∠OCE==．
故答案为．
怎样要将一个如图所示的破镜重圆？.拓展探究