安徽省蚌埠市第一实验学校202-2023学年九年级上学期第一次月考数学试卷(含答案)
文档属性
| 名称 | 安徽省蚌埠市第一实验学校202-2023学年九年级上学期第一次月考数学试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-09 21:53:57 | ||
图片预览


文档简介
2022-2023学年九年级上学期第一次调研数学试卷
注意事项
1.你拿到的试卷满分为150分,考试时间为120分钟。
2.试卷包括“试题卷”和“答题卷”两部分,“试题卷”共4页。“答题卷”共6页。
3.请务必在“答题卷”上答题,在“试题卷”上答题是无效的。
一、选择题(本大题共10小题,每小题4分,满分40分)
1.下列函数中,是二次函数的是
A.y=+x+1 B.y=x -(x+1)2 C.y=-x2+3x+1 D.y=3x+1
2.将抛物线y=2x 先向右平移2个单位,再向上平移3个单位后,得到的抛物线的表达式是
A.y=2(x-2)2-3 B.y=2(x-2)2+3 C.y=2(x+2)2-3 D.y=2(x+2)2+3
3.已知撤物线的顶点坐标是(2,-1),且与y轴交于点(0,3),这个抛物线的表达式是 ( )A.y=x -4x+3 B.y=x +4x+3 C.y=x +4x-1 D.y=x -4x-1
4.二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中不正确的是()
A.abc<0 B.b=-4a C.4a+2b≥m(am+b) D.a-b+c>0
5.若二次函数y=(x-m) +h,当x<1时,y随x的增大而减小,则m的取值范围是()
A.m=1 B.m>1 C.m≥1 D.m<1
6.已知二次函数y=kx -3x+2的图象和x轴有交点,则k的取值范围是()
A.k<且k≠0 B.k< C.k≤且k≠o D.k≤
7.如图,某同学以抛物线为灵感,在平面直角坐标系中设计了一款高OD为14的奖杯,杯体轴截面ABC是抛物线y=x2+5的一部分,则杯口的口径AC为()
A.9 B.8 C.7 D.10
8.点C为线段AB上的一个动点,AB=1,分别以AC和CB为一边作等边三角形,用S表示这
两个等边三角形的面积之和,下列判断正确的是()
当C为AB的三等分点时,S最小 B.当C是AB的中点时,S最大
C.当C为AB的三等分点时,S最大 D.当C是AB的中点时,S最小
9.若二次函数y=ax2+bx+c的图象经过A(x1,y1),B(x1,y2),C(4-m,m),D(m,n)(y1≠n),则下列命题正确的是
A.若a>0且|x1-2|>|x2-2|,则y1B.若a<0且y1C.若|x1-2|>|x2-2|且y1>y2,则a<0
D.若x1+x2=4(x1≠x2),则AB//CD
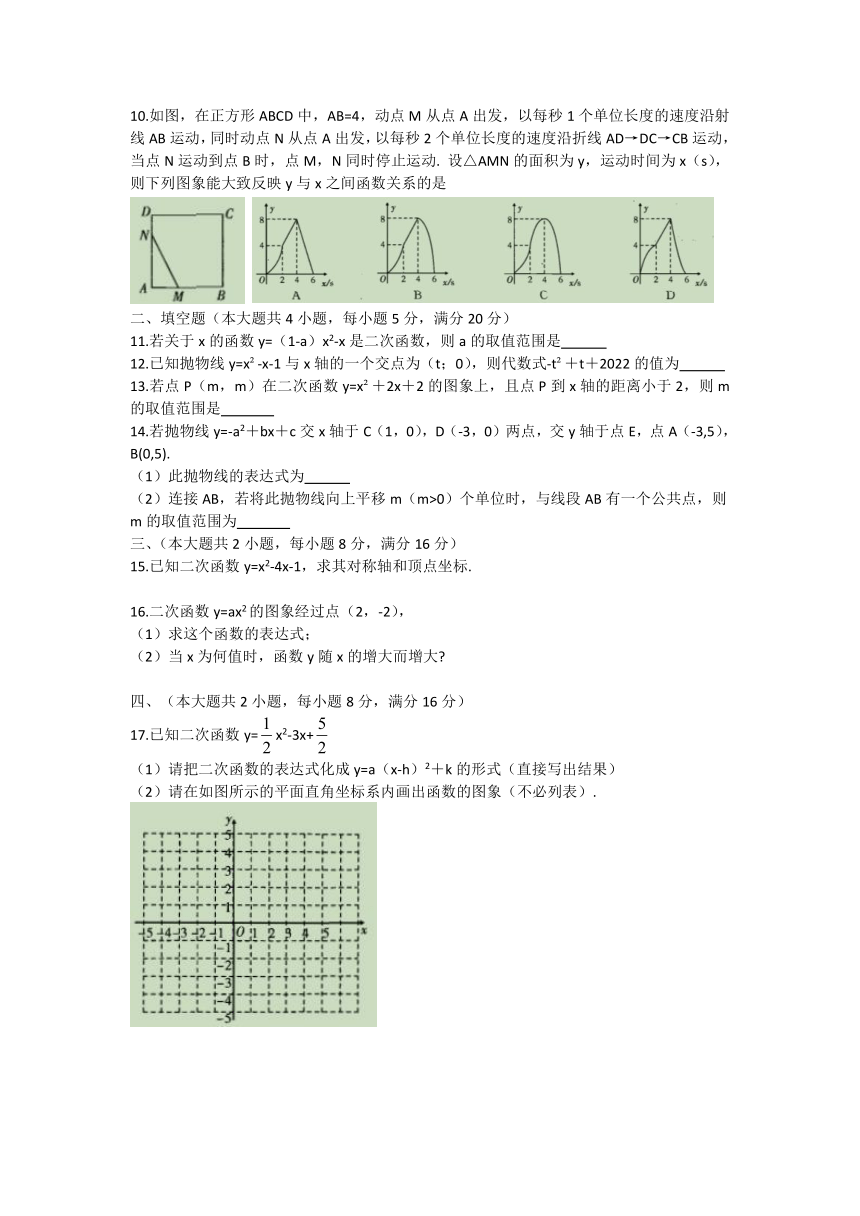
10.如图,在正方形ABCD中,AB=4,动点M从点A出发,以每秒1个单位长度的速度沿射线AB运动,同时动点N从点A出发,以每秒2个单位长度的速度沿折线AD→DC→CB运动,当点N运动到点B时,点M,N同时停止运动. 设△AMN的面积为y,运动时间为x(s),则下列图象能大致反映y与x之间函数关系的是
二、填空题(本大题共4小题,每小题5分,满分20分)
11.若关于x的函数y=(1-a)x2-x是二次函数,则a的取值范围是
12.已知抛物线y=x -x-1与x轴的一个交点为(t;0),则代数式-t +t+2022的值为
13.若点P(m,m)在二次函数y=x +2x+2的图象上,且点P到x轴的距离小于2,则m的取值范围是
14.若抛物线y=-a2+bx+c交x轴于C(1,0),D(-3,0)两点,交y轴于点E,点A(-3,5),B(0,5).
(1)此抛物线的表达式为
(2)连接AB,若将此抛物线向上平移m(m>0)个单位时,与线段AB有一个公共点,则m的取值范围为
三、(本大题共2小题,每小题8分,满分16分)
15.已知二次函数y=x2-4x-1,求其对称轴和顶点坐标.
16.二次函数y=ax2的图象经过点(2,-2),
(1)求这个函数的表达式;
(2)当x为何值时,函数y随x的增大而增大
(本大题共2小题,每小题8分,满分16分)
17.已知二次函数y=x2-3x+
(1)请把二次函数的表达式化成y=a(x-h)2+k的形式(直接写出结果)
(2)请在如图所示的平面直角坐标系内画出函数的图象(不必列表).
18.在平面直角坐标系xOy中,关于x的二次函数y=x +px+q的图象经过点(-1,0),(2,0),
(1)求这个二次函数的表达式
(2)求当-2≤x≤1时,y的最大值与最小值的差;
(3)直接写出使y<0的x的取值范围.
(本大题共2小题,每小题10分,满分20分)
19.已知二次函数y=x2+2mx-2m-1(m为常数).
(1)当m=-1时,此函数的图象与x轴有几个交点
(2)求证∶不论m为何值,该二次函数的图象与x轴总有公共点.
20.某农场计划建造一个矩形养殖场,为充分利用现有资源,该矩形养殖场一面靠墙(墙的长度为10m),另外三面用栅栏围成,中间再用栅栏把它分成两个面积为1∶2的矩形,已知栅栏的总长度为24m,设较小矩形的宽为xm(如图).
(1)若矩形养殖场的总面积为36m ,求此时x的值;
(2)当x为多少时,矩形养殖场的总面积最大 最大值为多少
六、(本题满分12分)
21.鲜埠,古乃采珠之地,素有“珍珠城”之美誉,已知一批珍珠每颗的进价为30元,售价定为50元/颗时,每天可销售60颗,为扩大市场占有率,商家决定采取适当的降价措施,经调查发现,售价每降低2元,每天销量可增加20颗(销售单价不低于进价).
(1)写出商家每天的利润W(元)与降价x(元)之间的函数关系;
(2)当降价多少元时,商家每天的利润最大,最大利润是多少
(3)若商家每天的利润至少要达到1440元,则定价应在什么范围内
七、(本题满分12分)
22.如图,已知抛物线y=ax2+3ax+c(a>0)与y轴交于点C,与z轴交于A,B两点,点A在点B左侧.点B的坐标为(1,0),0C=3OB.
(1)求抛物线的表达式
(2)若点D是线段AC下方抛物线上的动点,求△ACD面积的最大值.
八、(本题满分14分)
23.在平面直角坐标系中,抛物线y=ax2-2ax-3a(a≠0)的顶点为P,且该抛物线与x轴交于A,B两点(点A在点B的左侧).我们规定;抛物线与x轴围成的封闭区域称为“G区城"(不包含边界),横、纵坐标都是整数的点称为整点.
求抛物线y=ax -2ax-3a的顶点P的坐标(用含a的代数式表示);
(2)如果抛物线y=ax2-2ax-3a经过(1,3).
①求a的值
②在①的条件下,直接写出“G区域”内整点的坐标;
(3)如果抛物线y=ax2-2ax-3a在"G区域"内有4个整点,求a的取值范围,
注意事项
1.你拿到的试卷满分为150分,考试时间为120分钟。
2.试卷包括“试题卷”和“答题卷”两部分,“试题卷”共4页。“答题卷”共6页。
3.请务必在“答题卷”上答题,在“试题卷”上答题是无效的。
一、选择题(本大题共10小题,每小题4分,满分40分)
1.下列函数中,是二次函数的是
A.y=+x+1 B.y=x -(x+1)2 C.y=-x2+3x+1 D.y=3x+1
2.将抛物线y=2x 先向右平移2个单位,再向上平移3个单位后,得到的抛物线的表达式是
A.y=2(x-2)2-3 B.y=2(x-2)2+3 C.y=2(x+2)2-3 D.y=2(x+2)2+3
3.已知撤物线的顶点坐标是(2,-1),且与y轴交于点(0,3),这个抛物线的表达式是 ( )A.y=x -4x+3 B.y=x +4x+3 C.y=x +4x-1 D.y=x -4x-1
4.二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中不正确的是()
A.abc<0 B.b=-4a C.4a+2b≥m(am+b) D.a-b+c>0
5.若二次函数y=(x-m) +h,当x<1时,y随x的增大而减小,则m的取值范围是()
A.m=1 B.m>1 C.m≥1 D.m<1
6.已知二次函数y=kx -3x+2的图象和x轴有交点,则k的取值范围是()
A.k<且k≠0 B.k< C.k≤且k≠o D.k≤
7.如图,某同学以抛物线为灵感,在平面直角坐标系中设计了一款高OD为14的奖杯,杯体轴截面ABC是抛物线y=x2+5的一部分,则杯口的口径AC为()
A.9 B.8 C.7 D.10
8.点C为线段AB上的一个动点,AB=1,分别以AC和CB为一边作等边三角形,用S表示这
两个等边三角形的面积之和,下列判断正确的是()
当C为AB的三等分点时,S最小 B.当C是AB的中点时,S最大
C.当C为AB的三等分点时,S最大 D.当C是AB的中点时,S最小
9.若二次函数y=ax2+bx+c的图象经过A(x1,y1),B(x1,y2),C(4-m,m),D(m,n)(y1≠n),则下列命题正确的是
A.若a>0且|x1-2|>|x2-2|,则y1
D.若x1+x2=4(x1≠x2),则AB//CD
10.如图,在正方形ABCD中,AB=4,动点M从点A出发,以每秒1个单位长度的速度沿射线AB运动,同时动点N从点A出发,以每秒2个单位长度的速度沿折线AD→DC→CB运动,当点N运动到点B时,点M,N同时停止运动. 设△AMN的面积为y,运动时间为x(s),则下列图象能大致反映y与x之间函数关系的是
二、填空题(本大题共4小题,每小题5分,满分20分)
11.若关于x的函数y=(1-a)x2-x是二次函数,则a的取值范围是
12.已知抛物线y=x -x-1与x轴的一个交点为(t;0),则代数式-t +t+2022的值为
13.若点P(m,m)在二次函数y=x +2x+2的图象上,且点P到x轴的距离小于2,则m的取值范围是
14.若抛物线y=-a2+bx+c交x轴于C(1,0),D(-3,0)两点,交y轴于点E,点A(-3,5),B(0,5).
(1)此抛物线的表达式为
(2)连接AB,若将此抛物线向上平移m(m>0)个单位时,与线段AB有一个公共点,则m的取值范围为
三、(本大题共2小题,每小题8分,满分16分)
15.已知二次函数y=x2-4x-1,求其对称轴和顶点坐标.
16.二次函数y=ax2的图象经过点(2,-2),
(1)求这个函数的表达式;
(2)当x为何值时,函数y随x的增大而增大
(本大题共2小题,每小题8分,满分16分)
17.已知二次函数y=x2-3x+
(1)请把二次函数的表达式化成y=a(x-h)2+k的形式(直接写出结果)
(2)请在如图所示的平面直角坐标系内画出函数的图象(不必列表).
18.在平面直角坐标系xOy中,关于x的二次函数y=x +px+q的图象经过点(-1,0),(2,0),
(1)求这个二次函数的表达式
(2)求当-2≤x≤1时,y的最大值与最小值的差;
(3)直接写出使y<0的x的取值范围.
(本大题共2小题,每小题10分,满分20分)
19.已知二次函数y=x2+2mx-2m-1(m为常数).
(1)当m=-1时,此函数的图象与x轴有几个交点
(2)求证∶不论m为何值,该二次函数的图象与x轴总有公共点.
20.某农场计划建造一个矩形养殖场,为充分利用现有资源,该矩形养殖场一面靠墙(墙的长度为10m),另外三面用栅栏围成,中间再用栅栏把它分成两个面积为1∶2的矩形,已知栅栏的总长度为24m,设较小矩形的宽为xm(如图).
(1)若矩形养殖场的总面积为36m ,求此时x的值;
(2)当x为多少时,矩形养殖场的总面积最大 最大值为多少
六、(本题满分12分)
21.鲜埠,古乃采珠之地,素有“珍珠城”之美誉,已知一批珍珠每颗的进价为30元,售价定为50元/颗时,每天可销售60颗,为扩大市场占有率,商家决定采取适当的降价措施,经调查发现,售价每降低2元,每天销量可增加20颗(销售单价不低于进价).
(1)写出商家每天的利润W(元)与降价x(元)之间的函数关系;
(2)当降价多少元时,商家每天的利润最大,最大利润是多少
(3)若商家每天的利润至少要达到1440元,则定价应在什么范围内
七、(本题满分12分)
22.如图,已知抛物线y=ax2+3ax+c(a>0)与y轴交于点C,与z轴交于A,B两点,点A在点B左侧.点B的坐标为(1,0),0C=3OB.
(1)求抛物线的表达式
(2)若点D是线段AC下方抛物线上的动点,求△ACD面积的最大值.
八、(本题满分14分)
23.在平面直角坐标系中,抛物线y=ax2-2ax-3a(a≠0)的顶点为P,且该抛物线与x轴交于A,B两点(点A在点B的左侧).我们规定;抛物线与x轴围成的封闭区域称为“G区城"(不包含边界),横、纵坐标都是整数的点称为整点.
求抛物线y=ax -2ax-3a的顶点P的坐标(用含a的代数式表示);
(2)如果抛物线y=ax2-2ax-3a经过(1,3).
①求a的值
②在①的条件下,直接写出“G区域”内整点的坐标;
(3)如果抛物线y=ax2-2ax-3a在"G区域"内有4个整点,求a的取值范围,
同课章节目录
