2022-2023学年人教版数学八年级上册12.2三角形全等的判定 课时练习(含答案)
文档属性
| 名称 | 2022-2023学年人教版数学八年级上册12.2三角形全等的判定 课时练习(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 673.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-10 00:00:00 | ||
图片预览

文档简介
三角形全等的判定
一、单选题
1.如图,在△AED和△CFB中,已知BE=DF,添加下列一组条件后,不能判定△AED≌△CFB的是( )
A.BC=AD,CF=AE B.∠B=∠D,CF=AE
C.BC=AD,∠B=∠D D.∠B=∠D,∠C=∠A
2.如图,在2×2的方格纸中,∠1+∠2等于( )
A.60° B.90° C.120° D.150°
3.如图,下列条件中,不能证明△ABC≌△DCB的是( )
A.AB=DC,AC=DB B.AB=DC,∠ABC=∠DCB
C.∠ACB=∠DBC,∠A=∠D D.AB=DC,∠DBC=∠ACB
4.如图,在△PAB中,∠A=∠B,M,N,K分别是PA,PB,AB上的点,且AM=BK,BN=AK,若∠MKN=44°,则∠P的度数为( )
A.44° B.66° C.88° D.92°
5.如图,在△ABC中,AB=6,AC=8,AD是边BC上的中线,则AD长的取值范围是( )
A.6<AD<8 B.6≤AD≤8 C.1<AD<7 D.1≤AD≤7
6.如图,要测量河两岸相对的两点A、B的距离,先在AB的垂线BF上取两点C、D,使BC=CD,再作出BF的垂线DE,使点A、C、E在同一条直线上(如图),可以说明△ABC≌△EDC,得AB=DE,因此测得DE的长就是AB的长,判定△ABC≌△EDC,最恰当的理由是( )
A.SAS B.HL C.SSS D.ASA
7.如图,在平面直角坐标系中,点A在y轴上,点B在x轴上,AB=AC,∠BAC=90°,CM⊥y轴于点M.若C点坐标为(-3,-4),则B点坐标为( )
A.(5,0) B.(6,0) C.(7,0) D.(8,0)
8.如图,已知,点D、E分别在AB、AC上,且,连接CD、BE,CD与BE相交于点O,则下列结论错误的是( )
A. B. C. D.
9.如图,把两根钢条的中点连在一起,可以做成一个测量工件内槽宽的工具(卡钳),要测量工件内槽宽AB,只需测量的长度即可.的依据是( )
A.SSS B.SAS C.ASA D.AAS
10.如图,在△ABC中,AB=BC,点D为AC上的点,连接BD,点E在△ABC外,连接AE,BE,使得CD=BE,∠ABE=∠C,过点B作BF⊥AC交AC点F,若∠BAE=21°,∠C=28°,则∠FBD=( )
A.49° B.59° C.41° D.51°
11.如图,是的中线,E,F分别是和延长线上的点,且,连接.下列说法:①;②和面积相等;③;④.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
12.如图,AD=BC,AE=CF.E、F是BD上两点,BE=DF,∠AEB=100°,∠ADB=30°,则∠BCF的度数为( )
A.30° B.60° C.70° D.80°
二、填空题
13.如图,点A、B、C、D在同一条直线上,AB = CD,AE = DF,CE= BF.若∠A=55°,∠E=84°,则∠DBF的大小为__________
14.如图所示,AB=AC,AD=AE,∠BAC=∠DAE,∠1=28°,∠2=30°,则∠3=_____.
15.如图,小王想测量小口瓶下半部的内径,他把两根长度相等的钢条AA′,BB′的中点连在一起,A,B两点可活动,使M,N卡在瓶口的内壁上,A′,B′卡在小口瓶下半部的瓶壁上,然后量出AB=15cm,就可得出小口瓶下半部的内径是_______.
16.如图,点B、C、E在同一条直线上,,,,,则___________.
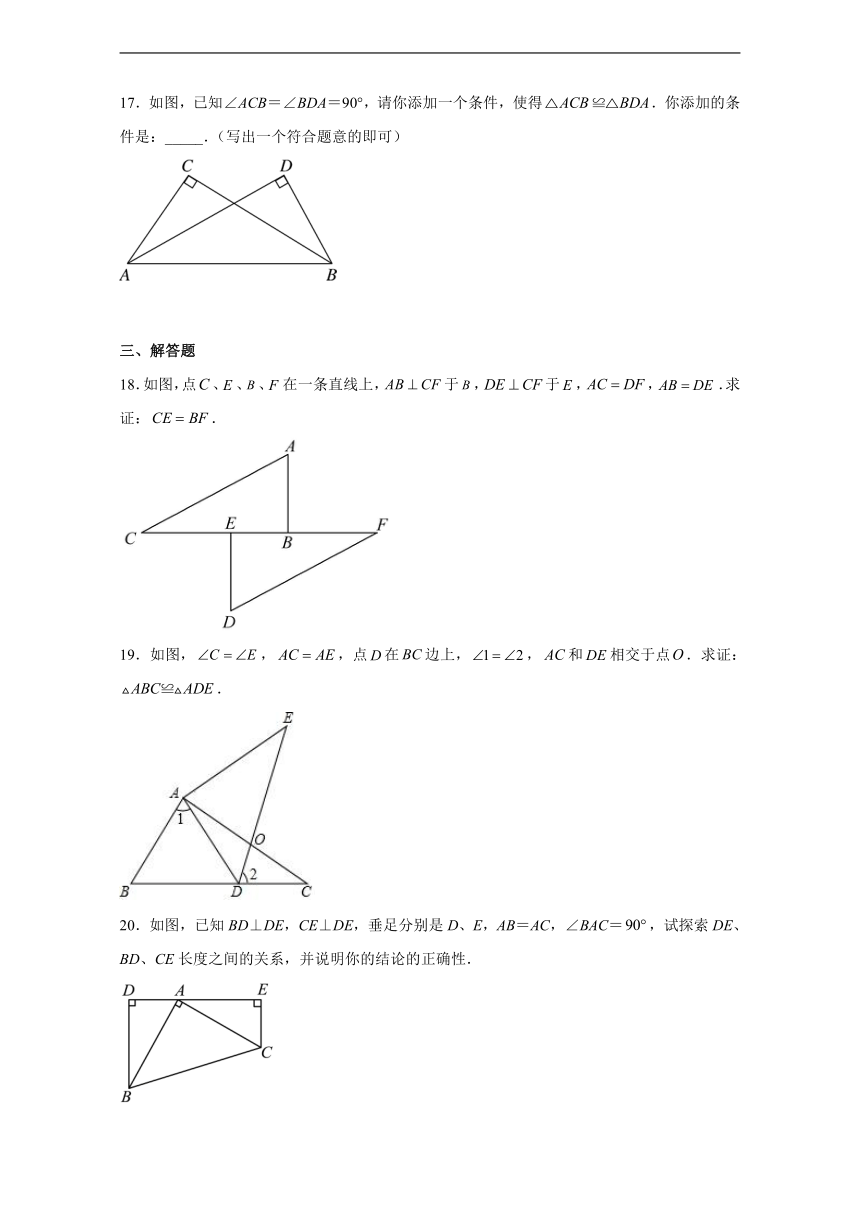
17.如图,已知∠ACB=∠BDA=90°,请你添加一个条件,使得.你添加的条件是:_____.(写出一个符合题意的即可)
三、解答题
18.如图,点、、、在一条直线上,于,于,,.求证:.
19.如图,,,点在边上,,和相交于点.求证:.
20.如图,已知BD⊥DE,CE⊥DE,垂足分别是D、E,AB=AC,∠BAC=,试探索DE、BD、CE长度之间的关系,并说明你的结论的正确性.
21.如图,在中,,,是斜边上的一点,于,交的延长线于.
(1)求证:≌;
(2)求证:.
22.在△ABC中,AB=AC,点D是直线BC上一点(点D不与点B,C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.
(1)求证:△ABD≌△ACE;
(2)∠BCE和∠BAC之间有怎样的数量关系?说明理由.
参考答案:
1.B
解:由BE=DF可得,即.
A选项,添加BC=AD,CF=AE后,△AED和△CFB中,满足三组对边相等,能够判定△AED≌△CFB,不符合题意;
B选项,添加∠B=∠D,CF=AE后,△AED和△CFB中,满足两组对边相等,一组对角相等,但该组对角不是两组对边的夹角,不能判定△AED≌△CFB,符合题意;
C选项,添加BC=AD,∠B=∠D后,△AED和△CFB中,满足两组对边相等,且两组对边的夹角相等,能够判定△AED≌△CFB,不符合题意;
D选项,添加∠B=∠D,∠C=∠A后,△AED和△CFB中,满足一组对边相等,两组对角相等,能够判定△AED≌△CFB,不符合题意;
故选B.
2.B
解:如图,在△ABC和△DEA中,
,
∴△ABC≌△DEA(SAS),
∴∠2=∠3,
在Rt△ABC中,∠1+∠3=90°,
∴∠1+∠2=90°.
故选:B.
3.D
解:根据题意知,BC=BC.
A、由“SSS”可以判定△ABC≌△DCB,故本选项不符合题意;
B、由“SAS”可以判定△ABC≌△DCB,故本选项不符合题意;
C、由“AAS”可以判定△ABC≌△DCB,故本选项不符合题意;
D、由“SSA”不能判定△ABC≌△DCB,故本选项符合题意.
故选:D.
4.D
解:∵PA=PB,
∴∠A=∠B,
在△AMK和△BKN中,
,
∴△AMK≌△BKN,
∴∠AMK=∠BKN,
∵∠MKB=∠MKN+∠NKB=∠A+∠AMK,
∴∠A=∠MKN=44°,
∴∠P=180°﹣∠A﹣∠B=92°,
故选:D.
5.C
解:如图,延长AD至点E,使AD=DE,连接CE,
∵AD是边BC上的中线,
∴CD=BD,
在△ABD和△CED中,
,
∴△ABD≌△CED,
∴AB=CE=6,
在△ACE中,8-6∴1<AD<7,
故选:C.
6.D
解:因为证明在△ABC≌△EDC用到的条件是:CD=BC,∠ABC=∠EDC=90°,∠ACB=∠ECD,
所以用到的是两角及这两角的夹边对应相等即ASA这一方法.
故选:D.
7.C
解:∵C点坐标为(-3,-4),
∴CM=3,OM=4,
∵∠BOA=90°,
∴∠BAO+∠ABO=90°,
又∵∠BAC=∠BAO+∠CAM=90°,
∴∠ABO=∠CAM;
∵CM⊥y轴,
∴∠AMC=∠BOA=90°,
在△AMC和△BOA中,
∴△AMC≌△BOA(AAS),
∴CM=AO=3,AM=BO,
∴AM=OA+OM=3+4=7,
∴OB=7,
∴B(7,0).
故选:C.
8.C
解:∵AB=AC,AE=AD,∠A=∠A,
∴△ABE≌△ACD(SAS),
∴∠B=∠C,故A正确,不符合题意;
∵AB=AD,AD=AE,
∴AB-AD=AC-AE,
∴BD=CE,故B正确,不符合题意;
又∵∠B=∠C,∠DOB=∠EOC,
∴△OBD≌△OCE(AAS),故D正确,不符合题意;
根据现有条件无法证明OC=OD,故C错误,符合题意;
故选C.
9.B
解:根据题意有:,(对顶角相等),,
即有(SAS),
故选:B.
10.C
解:在△ABE和△BCD中,
,
∴△ABE≌△BCD(SAS),
∴∠BAE=∠CBD,
∵∠BAE=21°,∠C=28°,
∴∠CBD=21°,
∴∠BDF=∠CBD+∠C=21°+28°=49°,
∵BF⊥AC,
∴∠BFD=90°,
∴∠FBD=90°﹣∠BDF=90°﹣49°=41°
故选:C.
11.D
解:是的中线,
,
在和中,
,
,故④正确
,,故①正确,
,故③正确,
,点到、的距离相等,
和面积相等,故②正确,
综上所述,正确的有4个,
故选:D.
12.C
解:∵BE=DF,
∴BE+EF=DF+EF,
∴BF=DE
又∵AD=BC,AE=CF.
∴△AED≌△CFB(SSS),
∴∠BCF=∠DAE,
∵∠DAE=∠AEB ∠ADB=100°-30°=70°
∴∠BCF=70°.
故选C.
13.41°
解:∵AB = CD,
∴AB+BC=CD+BC,即:AC=BD,
在△ACE和△DBF中,
,
∴在△ACE≌△DBF(SSS),
∴∠A=∠D=55°,∠E=∠F=84°,
∴∠DBF=180°-55°-84°=41°,
故答案为:41°.
14.58°
解:∵∠BAC=∠DAE,
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,
∴∠1=∠EAC,
在△BAD和△CAE中,
,
∴△BAD≌△CAE(SAS),
∴∠2=∠ABD=30°,
∵∠1=28°,
∴∠3=∠1+∠ABD=28°+30°=58°,
故答案为:58°.
15.15cm
解:∵O为AA′、BB′的中点,
∴AO=A′O,BO=B′O.
在△AOB和△B′OA′中,
,
∴△AOB≌△B′OA′(SAS).
∴AB=A′B′=15cm.
故答案为:15cm.
16.9
解:∵∠B=∠E=∠ACF=60°,
∠BCA+∠ACF=∠CFE+∠E,
∠ACF+∠ECF=∠B+∠BAC
∴∠BCA=∠CFE
∠BAC=∠ECF
∴
∴BC=EF,AB=CE
∴BE=BC+CE=EF+AB=5+4=9
17.AC=BD(答案不唯一)
解:添加的条件是AC=BD(答案不唯一),理由如下:
∵∠ACB=∠BDA=90°,
∴△ACB和△BDA是直角三角形,
在Rt△ACB和Rt△BDA中,
,
∴△ACB≌△BDA(HL),
故答案为:AC=BD(答案不唯一).
18.证明见解析
解:∵,,
∴,
在和中,
,
∴≌(HL),
∴,
∴,
即:.
19.见解析
解:∵,
即,
∵,
∴,
在和中,
∴.
20.DE=BD+CE,见解析
解:结论:DE=BD+CE.证明如下:
如图,
∵∠BAC=,
∴∠EAC+∠DAB=,
∵BD⊥DE,CE⊥DE,
∴∠DAB+∠DBA=,∠D=∠E=,
∴∠EAC=∠DBA,
在△ABD和△CAE中,
∵,
∴△ABD≌△CAE,
∴AD=CE,BD=AE,
∴DE=AD+AE=CE+BD.
21.(1)见解析
(2)见解析
证明:,
,
,
,
,
,,
,
在与中,
,
≌;
(2)
证明:,
,
,
,
,
,,
,
在与中,
,
≌,
,,
.
22.(1)见解析
(2)∠BAC+∠BCE=180°,见解析
(1)
证明:∵∠BAC=∠DAE,
∴∠BAD=∠CAE,
在△ABD与△ACE中,
,
∴△ABD≌△ACE(SAS);
(2)
解:∠BCE+∠BAC=180°.
理由:∵△ABD≌△ACE,
∴∠B=∠ACE,
∵∠BCE=∠ACE+∠ACB,
∴∠BCE=∠B+∠ACB,
∵∠B+∠ACB+∠BAC=180°,
∴∠BAC+∠BCE=180°.
一、单选题
1.如图,在△AED和△CFB中,已知BE=DF,添加下列一组条件后,不能判定△AED≌△CFB的是( )
A.BC=AD,CF=AE B.∠B=∠D,CF=AE
C.BC=AD,∠B=∠D D.∠B=∠D,∠C=∠A
2.如图,在2×2的方格纸中,∠1+∠2等于( )
A.60° B.90° C.120° D.150°
3.如图,下列条件中,不能证明△ABC≌△DCB的是( )
A.AB=DC,AC=DB B.AB=DC,∠ABC=∠DCB
C.∠ACB=∠DBC,∠A=∠D D.AB=DC,∠DBC=∠ACB
4.如图,在△PAB中,∠A=∠B,M,N,K分别是PA,PB,AB上的点,且AM=BK,BN=AK,若∠MKN=44°,则∠P的度数为( )
A.44° B.66° C.88° D.92°
5.如图,在△ABC中,AB=6,AC=8,AD是边BC上的中线,则AD长的取值范围是( )
A.6<AD<8 B.6≤AD≤8 C.1<AD<7 D.1≤AD≤7
6.如图,要测量河两岸相对的两点A、B的距离,先在AB的垂线BF上取两点C、D,使BC=CD,再作出BF的垂线DE,使点A、C、E在同一条直线上(如图),可以说明△ABC≌△EDC,得AB=DE,因此测得DE的长就是AB的长,判定△ABC≌△EDC,最恰当的理由是( )
A.SAS B.HL C.SSS D.ASA
7.如图,在平面直角坐标系中,点A在y轴上,点B在x轴上,AB=AC,∠BAC=90°,CM⊥y轴于点M.若C点坐标为(-3,-4),则B点坐标为( )
A.(5,0) B.(6,0) C.(7,0) D.(8,0)
8.如图,已知,点D、E分别在AB、AC上,且,连接CD、BE,CD与BE相交于点O,则下列结论错误的是( )
A. B. C. D.
9.如图,把两根钢条的中点连在一起,可以做成一个测量工件内槽宽的工具(卡钳),要测量工件内槽宽AB,只需测量的长度即可.的依据是( )
A.SSS B.SAS C.ASA D.AAS
10.如图,在△ABC中,AB=BC,点D为AC上的点,连接BD,点E在△ABC外,连接AE,BE,使得CD=BE,∠ABE=∠C,过点B作BF⊥AC交AC点F,若∠BAE=21°,∠C=28°,则∠FBD=( )
A.49° B.59° C.41° D.51°
11.如图,是的中线,E,F分别是和延长线上的点,且,连接.下列说法:①;②和面积相等;③;④.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
12.如图,AD=BC,AE=CF.E、F是BD上两点,BE=DF,∠AEB=100°,∠ADB=30°,则∠BCF的度数为( )
A.30° B.60° C.70° D.80°
二、填空题
13.如图,点A、B、C、D在同一条直线上,AB = CD,AE = DF,CE= BF.若∠A=55°,∠E=84°,则∠DBF的大小为__________
14.如图所示,AB=AC,AD=AE,∠BAC=∠DAE,∠1=28°,∠2=30°,则∠3=_____.
15.如图,小王想测量小口瓶下半部的内径,他把两根长度相等的钢条AA′,BB′的中点连在一起,A,B两点可活动,使M,N卡在瓶口的内壁上,A′,B′卡在小口瓶下半部的瓶壁上,然后量出AB=15cm,就可得出小口瓶下半部的内径是_______.
16.如图,点B、C、E在同一条直线上,,,,,则___________.
17.如图,已知∠ACB=∠BDA=90°,请你添加一个条件,使得.你添加的条件是:_____.(写出一个符合题意的即可)
三、解答题
18.如图,点、、、在一条直线上,于,于,,.求证:.
19.如图,,,点在边上,,和相交于点.求证:.
20.如图,已知BD⊥DE,CE⊥DE,垂足分别是D、E,AB=AC,∠BAC=,试探索DE、BD、CE长度之间的关系,并说明你的结论的正确性.
21.如图,在中,,,是斜边上的一点,于,交的延长线于.
(1)求证:≌;
(2)求证:.
22.在△ABC中,AB=AC,点D是直线BC上一点(点D不与点B,C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.
(1)求证:△ABD≌△ACE;
(2)∠BCE和∠BAC之间有怎样的数量关系?说明理由.
参考答案:
1.B
解:由BE=DF可得,即.
A选项,添加BC=AD,CF=AE后,△AED和△CFB中,满足三组对边相等,能够判定△AED≌△CFB,不符合题意;
B选项,添加∠B=∠D,CF=AE后,△AED和△CFB中,满足两组对边相等,一组对角相等,但该组对角不是两组对边的夹角,不能判定△AED≌△CFB,符合题意;
C选项,添加BC=AD,∠B=∠D后,△AED和△CFB中,满足两组对边相等,且两组对边的夹角相等,能够判定△AED≌△CFB,不符合题意;
D选项,添加∠B=∠D,∠C=∠A后,△AED和△CFB中,满足一组对边相等,两组对角相等,能够判定△AED≌△CFB,不符合题意;
故选B.
2.B
解:如图,在△ABC和△DEA中,
,
∴△ABC≌△DEA(SAS),
∴∠2=∠3,
在Rt△ABC中,∠1+∠3=90°,
∴∠1+∠2=90°.
故选:B.
3.D
解:根据题意知,BC=BC.
A、由“SSS”可以判定△ABC≌△DCB,故本选项不符合题意;
B、由“SAS”可以判定△ABC≌△DCB,故本选项不符合题意;
C、由“AAS”可以判定△ABC≌△DCB,故本选项不符合题意;
D、由“SSA”不能判定△ABC≌△DCB,故本选项符合题意.
故选:D.
4.D
解:∵PA=PB,
∴∠A=∠B,
在△AMK和△BKN中,
,
∴△AMK≌△BKN,
∴∠AMK=∠BKN,
∵∠MKB=∠MKN+∠NKB=∠A+∠AMK,
∴∠A=∠MKN=44°,
∴∠P=180°﹣∠A﹣∠B=92°,
故选:D.
5.C
解:如图,延长AD至点E,使AD=DE,连接CE,
∵AD是边BC上的中线,
∴CD=BD,
在△ABD和△CED中,
,
∴△ABD≌△CED,
∴AB=CE=6,
在△ACE中,8-6
故选:C.
6.D
解:因为证明在△ABC≌△EDC用到的条件是:CD=BC,∠ABC=∠EDC=90°,∠ACB=∠ECD,
所以用到的是两角及这两角的夹边对应相等即ASA这一方法.
故选:D.
7.C
解:∵C点坐标为(-3,-4),
∴CM=3,OM=4,
∵∠BOA=90°,
∴∠BAO+∠ABO=90°,
又∵∠BAC=∠BAO+∠CAM=90°,
∴∠ABO=∠CAM;
∵CM⊥y轴,
∴∠AMC=∠BOA=90°,
在△AMC和△BOA中,
∴△AMC≌△BOA(AAS),
∴CM=AO=3,AM=BO,
∴AM=OA+OM=3+4=7,
∴OB=7,
∴B(7,0).
故选:C.
8.C
解:∵AB=AC,AE=AD,∠A=∠A,
∴△ABE≌△ACD(SAS),
∴∠B=∠C,故A正确,不符合题意;
∵AB=AD,AD=AE,
∴AB-AD=AC-AE,
∴BD=CE,故B正确,不符合题意;
又∵∠B=∠C,∠DOB=∠EOC,
∴△OBD≌△OCE(AAS),故D正确,不符合题意;
根据现有条件无法证明OC=OD,故C错误,符合题意;
故选C.
9.B
解:根据题意有:,(对顶角相等),,
即有(SAS),
故选:B.
10.C
解:在△ABE和△BCD中,
,
∴△ABE≌△BCD(SAS),
∴∠BAE=∠CBD,
∵∠BAE=21°,∠C=28°,
∴∠CBD=21°,
∴∠BDF=∠CBD+∠C=21°+28°=49°,
∵BF⊥AC,
∴∠BFD=90°,
∴∠FBD=90°﹣∠BDF=90°﹣49°=41°
故选:C.
11.D
解:是的中线,
,
在和中,
,
,故④正确
,,故①正确,
,故③正确,
,点到、的距离相等,
和面积相等,故②正确,
综上所述,正确的有4个,
故选:D.
12.C
解:∵BE=DF,
∴BE+EF=DF+EF,
∴BF=DE
又∵AD=BC,AE=CF.
∴△AED≌△CFB(SSS),
∴∠BCF=∠DAE,
∵∠DAE=∠AEB ∠ADB=100°-30°=70°
∴∠BCF=70°.
故选C.
13.41°
解:∵AB = CD,
∴AB+BC=CD+BC,即:AC=BD,
在△ACE和△DBF中,
,
∴在△ACE≌△DBF(SSS),
∴∠A=∠D=55°,∠E=∠F=84°,
∴∠DBF=180°-55°-84°=41°,
故答案为:41°.
14.58°
解:∵∠BAC=∠DAE,
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,
∴∠1=∠EAC,
在△BAD和△CAE中,
,
∴△BAD≌△CAE(SAS),
∴∠2=∠ABD=30°,
∵∠1=28°,
∴∠3=∠1+∠ABD=28°+30°=58°,
故答案为:58°.
15.15cm
解:∵O为AA′、BB′的中点,
∴AO=A′O,BO=B′O.
在△AOB和△B′OA′中,
,
∴△AOB≌△B′OA′(SAS).
∴AB=A′B′=15cm.
故答案为:15cm.
16.9
解:∵∠B=∠E=∠ACF=60°,
∠BCA+∠ACF=∠CFE+∠E,
∠ACF+∠ECF=∠B+∠BAC
∴∠BCA=∠CFE
∠BAC=∠ECF
∴
∴BC=EF,AB=CE
∴BE=BC+CE=EF+AB=5+4=9
17.AC=BD(答案不唯一)
解:添加的条件是AC=BD(答案不唯一),理由如下:
∵∠ACB=∠BDA=90°,
∴△ACB和△BDA是直角三角形,
在Rt△ACB和Rt△BDA中,
,
∴△ACB≌△BDA(HL),
故答案为:AC=BD(答案不唯一).
18.证明见解析
解:∵,,
∴,
在和中,
,
∴≌(HL),
∴,
∴,
即:.
19.见解析
解:∵,
即,
∵,
∴,
在和中,
∴.
20.DE=BD+CE,见解析
解:结论:DE=BD+CE.证明如下:
如图,
∵∠BAC=,
∴∠EAC+∠DAB=,
∵BD⊥DE,CE⊥DE,
∴∠DAB+∠DBA=,∠D=∠E=,
∴∠EAC=∠DBA,
在△ABD和△CAE中,
∵,
∴△ABD≌△CAE,
∴AD=CE,BD=AE,
∴DE=AD+AE=CE+BD.
21.(1)见解析
(2)见解析
证明:,
,
,
,
,
,,
,
在与中,
,
≌;
(2)
证明:,
,
,
,
,
,,
,
在与中,
,
≌,
,,
.
22.(1)见解析
(2)∠BAC+∠BCE=180°,见解析
(1)
证明:∵∠BAC=∠DAE,
∴∠BAD=∠CAE,
在△ABD与△ACE中,
,
∴△ABD≌△ACE(SAS);
(2)
解:∠BCE+∠BAC=180°.
理由:∵△ABD≌△ACE,
∴∠B=∠ACE,
∵∠BCE=∠ACE+∠ACB,
∴∠BCE=∠B+∠ACB,
∵∠B+∠ACB+∠BAC=180°,
∴∠BAC+∠BCE=180°.
