人教版八年级数学上册 13.3等腰三角形 同步达标测试题 2022-2023学年(含解析)
文档属性
| 名称 | 人教版八年级数学上册 13.3等腰三角形 同步达标测试题 2022-2023学年(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 189.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-10 10:03:07 | ||
图片预览

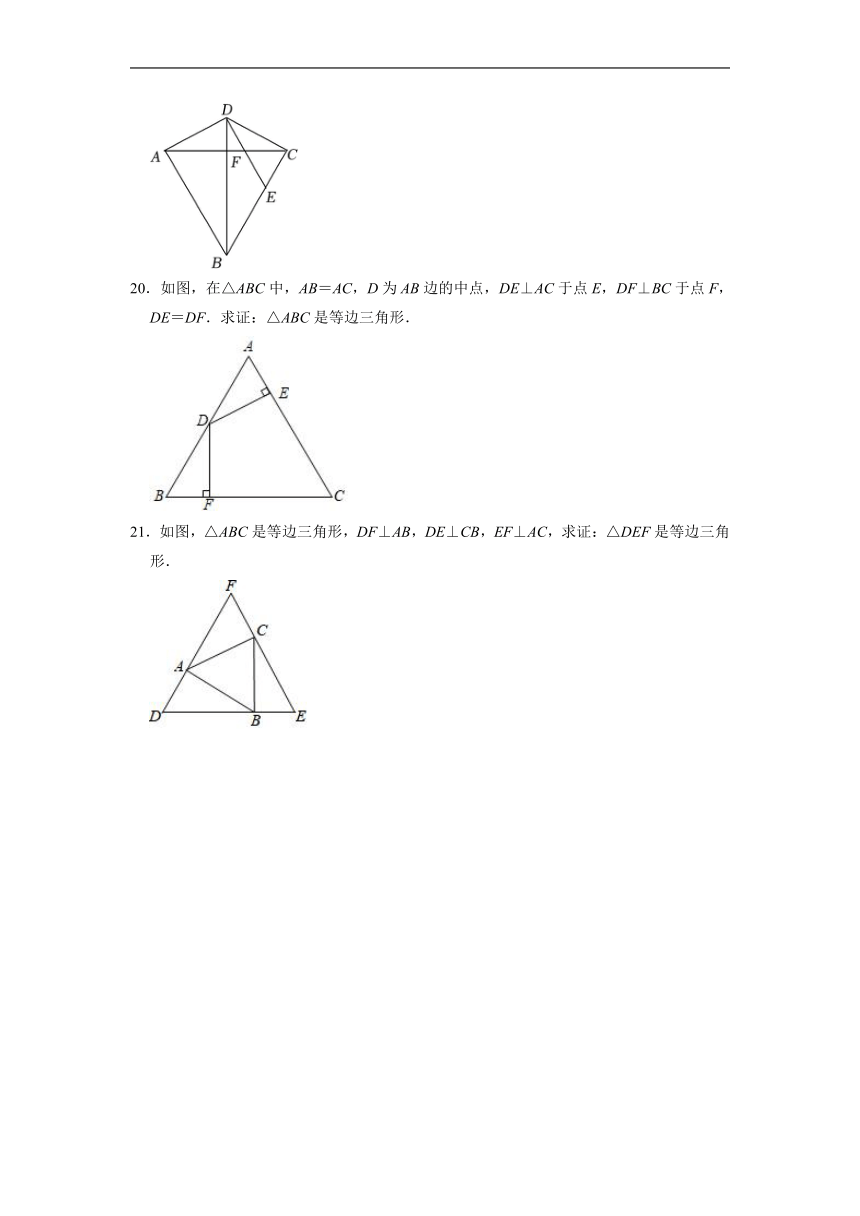

文档简介
2022-2023学年人教版八年级数学上册《13.3等腰三角形》同步达标测试题(附答案)
一.选择题(共8小题,满分32分)
1.若等腰三角形的两边长分别为2和5,则它的周长为( )
A.9 B.7 C.12 D.9或12
2.等腰三角形一边长等于2,一边长等于3,则它的周长是( )
A.5 B.7 C.8 D.7或8
3.如图,在直角三角形ABC中,∠ACB=90°,∠B=36°,点D、E在AB上,如果BC=BD,∠CED=∠CDE,那么图中的等腰三角形共有( )个.
A.3个 B.4个 C.5个 D.6个
4.如图,在△ABC中,∠ABC=3∠C,∠1=∠2,BE⊥AE,AB=5,BE=3,则AC=( )
A.10 B.11 C.13 D.15
5.如图,直线l1∥l2,将等边三角形如图放置若∠α=25°,则∠β等于( )
A.35° B.30° C.25° D.20°
6.三角形的三边长a,b,c满足(a﹣b)4+(b﹣c)2+|c﹣a|=0,那么这个三角形一定是( )
A.直角三角形 B.等边三角形
C.等腰非等边三角形 D.钝角三角形
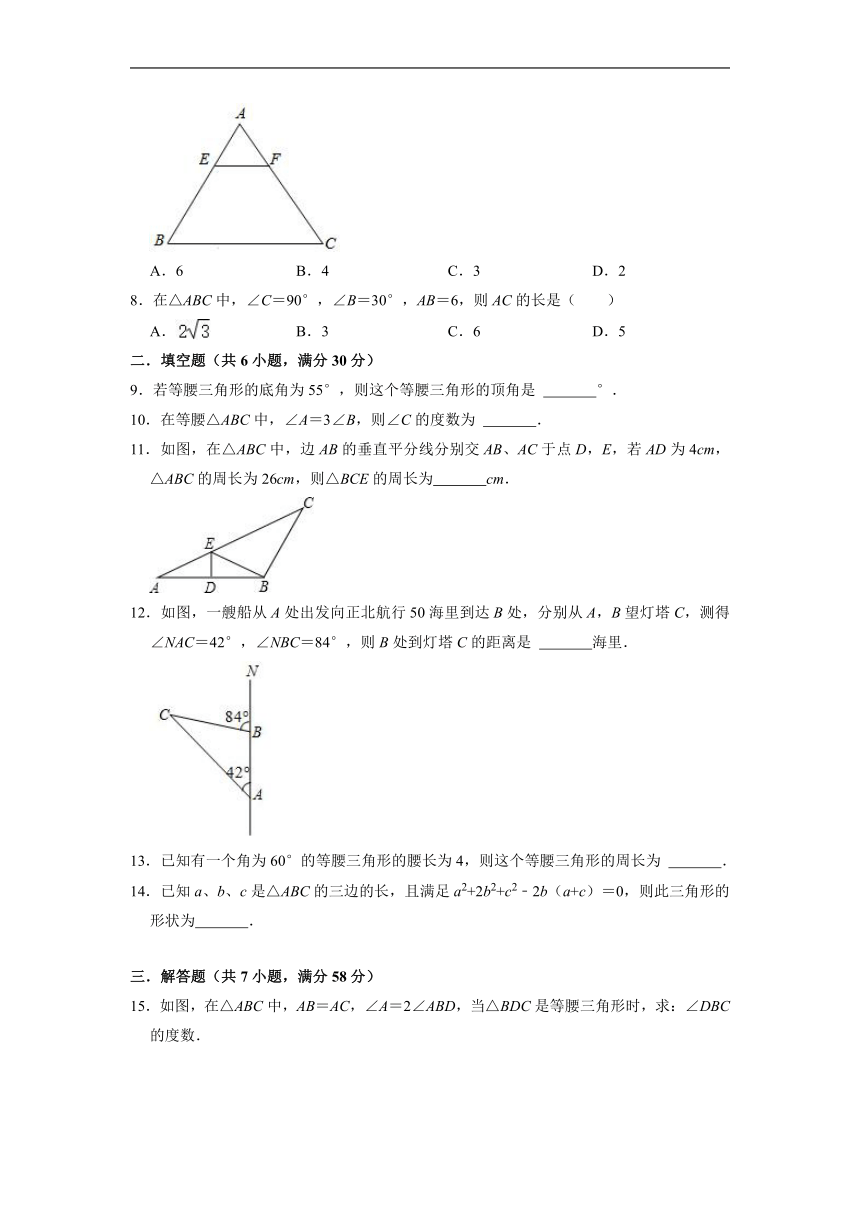
7.如图,△ABC是等边三角形,点E,F分别在AB,AC边上,且EF∥BC,若AB=6,BE=2,则EF的长为( )
A.6 B.4 C.3 D.2
8.在△ABC中,∠C=90°,∠B=30°,AB=6,则AC的长是( )
A. B.3 C.6 D.5
二.填空题(共6小题,满分30分)
9.若等腰三角形的底角为55°,则这个等腰三角形的顶角是 °.
10.在等腰△ABC中,∠A=3∠B,则∠C的度数为 .
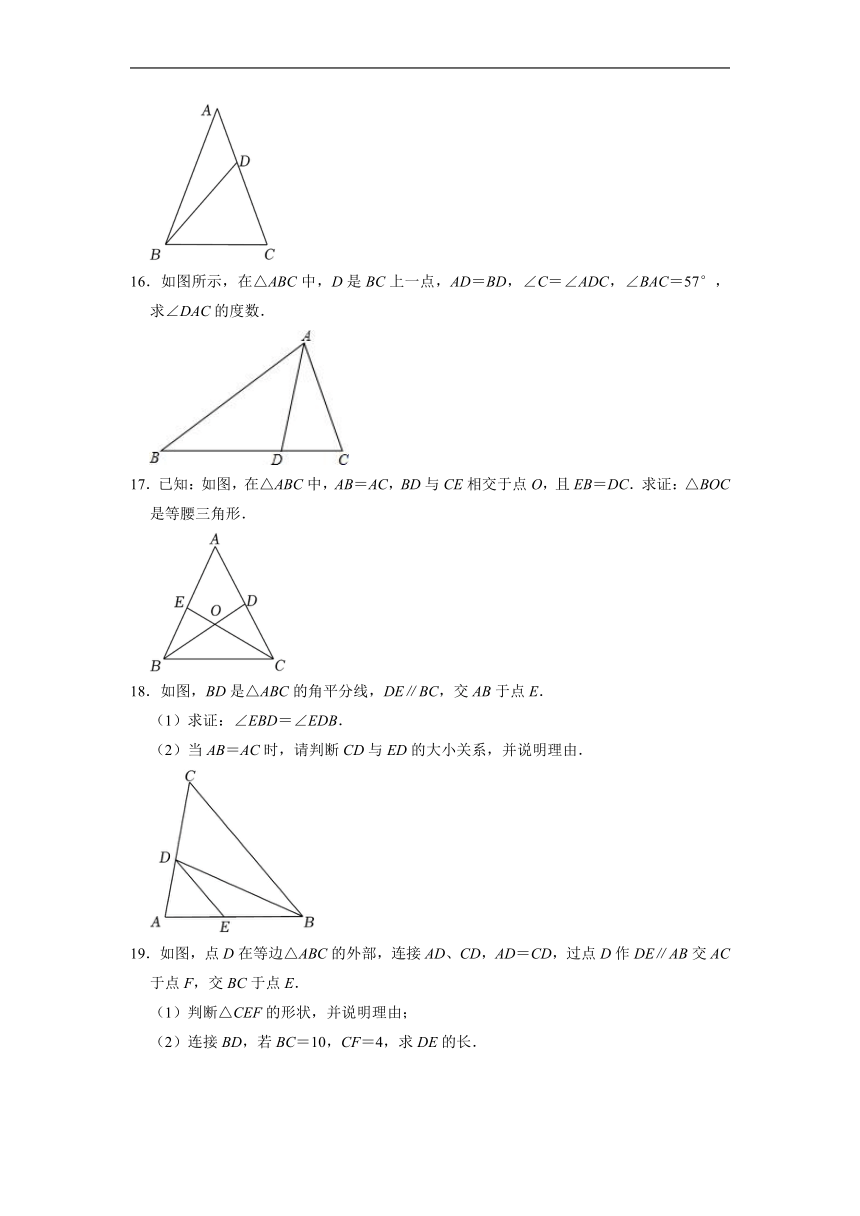
11.如图,在△ABC中,边AB的垂直平分线分别交AB、AC于点D,E,若AD为4cm,△ABC的周长为26cm,则△BCE的周长为 cm.
12.如图,一艘船从A处出发向正北航行50海里到达B处,分别从A,B望灯塔C,测得∠NAC=42°,∠NBC=84°,则B处到灯塔C的距离是 海里.
13.已知有一个角为60°的等腰三角形的腰长为4,则这个等腰三角形的周长为 .
14.已知a、b、c是△ABC的三边的长,且满足a2+2b2+c2﹣2b(a+c)=0,则此三角形的形状为 .
三.解答题(共7小题,满分58分)
15.如图,在△ABC中,AB=AC,∠A=2∠ABD,当△BDC是等腰三角形时,求:∠DBC的度数.
16.如图所示,在△ABC中,D是BC上一点,AD=BD,∠C=∠ADC,∠BAC=57°,求∠DAC的度数.
17.已知:如图,在△ABC中,AB=AC,BD与CE相交于点O,且EB=DC.求证:△BOC是等腰三角形.
18.如图,BD是△ABC的角平分线,DE∥BC,交AB于点E.
(1)求证:∠EBD=∠EDB.
(2)当AB=AC时,请判断CD与ED的大小关系,并说明理由.
19.如图,点D在等边△ABC的外部,连接AD、CD,AD=CD,过点D作DE∥AB交AC于点F,交BC于点E.
(1)判断△CEF的形状,并说明理由;
(2)连接BD,若BC=10,CF=4,求DE的长.
20.如图,在△ABC中,AB=AC,D为AB边的中点,DE⊥AC于点E,DF⊥BC于点F,DE=DF.求证:△ABC是等边三角形.
21.如图,△ABC是等边三角形,DF⊥AB,DE⊥CB,EF⊥AC,求证:△DEF是等边三角形.
参考答案
一.选择题(共8小题,满分32分)
1.解:(1)若2为腰长,5为底边长,
由于2+2<5,则三角形不存在;
(2)若5为腰长,则符合三角形的两边之和大于第三边.
所以这个三角形的周长为5+5+2=12.
故选:C.
2.解:分两种情况:
当腰为2时,2+2>3,所以能构成三角形,周长是2+2+3=7;
当腰为3时,3+2>3,所以能构成三角形,周长是:2+3+3=8.
故选:D.
3.解:∵∠ACB=90°,∠B=36°,
∴∠A=54°,
∵BC=BD,
∴∠CDB=∠DCB=72°,
∴∠ECB=36°,∠ACE=54°,
∴CE=BE,AE=CE,
∴△BCD,△CDE,△CEB,△ACE都是等腰三角形,
故选:B.
4.解:延长BE交AC于M,
∵BE⊥AE,
∴∠AEB=∠AEM=90°
∴∠3=90°﹣∠1,∠4=90°﹣∠2,
∵∠1=∠2,
∴∠3=∠4,
∴AB=AM=5,
∵BE⊥AE,
∴BM=2BE=6,
∵∠4是△BCM的外角,
∴∠4=∠5+∠C,
∵∠ABC=3∠C,
∴∠ABC=∠3+∠5=∠4+∠5,
∴3∠C=∠4+∠5=2∠5+∠C,
∴∠5=∠C,
∴CM=BM=6,
∴AC=AM+CM=AB+2BE=11.
故选:B.
5.解:过点B作BD∥l1,如图,
则∠ABD=∠α=25°.
∵l1∥l2,
∴BD∥l2,
∵∠DBC=∠β.
∵△ABC是等边三角形,
∴∠ABC=60°,
∴∠β=∠CBD=∠ABC﹣∠ABD=60°﹣25°=35°.
故选:A.
6.解:∵(a﹣b)4+(b﹣c)2+|c﹣a|=0,
∴a﹣b=0,b﹣c=0,c﹣a=0,
∴a=b=c.
又∵a,b,c是三角形的三边长,
∴这个三角形是等边三角形.
故选:B.
7.解:∵AB=6,BE=2,
∴AE=AB﹣BE=4,
∵△ABC是等边三角形,
∴∠A=∠B=∠C=60°,
∵EF∥BC,
∴∠AEF=∠B=60°,∠AFE=∠C=60°,
∴∠A=∠AEF=∠AFE=60°,
∴△AEF是等边三角形,
∴EF=AE=4.
故选:B.
8.解:∵∠C=90°,∠B=30°,AB=6,
∴AC=AB=×6=3,
故选:B.
二.填空题(共6小题,满分30分)
9.解:如图,在等腰△ABC中,
∵∠B=∠C=55°,∠A+∠B+∠C=180°,
∴∠A=180°﹣∠B﹣∠C,
=180°﹣55°﹣55°,
=70°;
故答案为:70.
10.解:设∠B=x°,则∠A=3x°,
当∠A是顶角时,∠A+2∠B=180°,
即:5x=180,
解得:x=36,
此时∠C=∠B=36°;
当∠A是底角时,∠A=∠C=3x°,
∠A+∠C+∠B=180°,
即7x=180,
解得:x=()°,
此时∠C=3x=()°,
故答案为:36°或()°.
11.解:∵ED垂直平分AB,
∴AE=BE,
∴BD=AD=4cm,AB=8cm,
∵△ABC的周长为26cm,
∴AC+BC=18cm,
△BCE的周长=BC+CE+AE=BC+CE+AE=18cm.
故填18.
12.解:根据题意得:AB=50海里,
∵∠NAC=42°,∠NBC=84°,
∴∠C=∠NBC﹣∠NAC=42°,
∴∠C=∠NAC,
∴BC=AB=50海里.
即从海岛B到灯塔C的距离是50海里.
故答案为:50.
13.解:由题意知,这个三角形为等边三角形,
∴周长为3×4=12,
故答案为:12.
14.解:由已知条件a2+2b2+c2﹣2b(a+c)=0化简得,
(a﹣b)2+(b﹣c)2=0
∴a﹣b=0,b﹣c=0
即 a=b,b=c
∴a=b=c
故答案为等边三角形.
三.解答题(共7小题,满分58分)
15.解:∵AB=AC,
∴∠ABC=∠C.
①当BD=CD时,∠C=∠CBD<∠ABC,故不成立;
②当BD=BC时,∠C=∠BDC=∠A+∠ABD,
∵∠A+∠ABC+∠C=180°,
∴∠A+∠A+∠ABD+∠A+∠ABD=180°,
∴3∠A+2∠ABD=180°,4∠A=180°,
∴∠A=45°,
∴∠ABD=22.5°,
∴∠ABC=(180°﹣45°)=67.5°,
∴∠DBC=∠ABC﹣∠ACD=45°;
③当CB=CD时,∠CBD=∠CDB=∠A+∠ABD,
设∠ABD=x,
∴∠A=2x,
∴∠CBD=∠CDB=3x,
∴∠ABC=∠C=4x,
∵∠A+∠ABC+∠C=180°,
∴2x+4x+4x=180°,
∴x=18°,
∴∠DBC=54°;
综上所述:∠DBC的度数为54°或45°.
16.解:∵AD=BD,
∴∠B=∠BAD,
∵∠ADC=∠B+∠BAD=2∠B,
∴∠C=2∠B,
∵∠BAC=57°,
∴∠B+∠C=3∠B=180°﹣∠BAC=41°,
∴∠ADC=∠C=82°,
∴∠DAC=16°.
17.证明:∵AB=AC,
∴∠ABC=∠ACB,
在△BEC与△CDB 中,
,
∴△BEC≌△CDB(SAS),
∴∠OCB=∠OBC,
∴OB=OC,
∴△BOC是等腰三角形.
18.(1)证明:∵BD是△ABC的角平分线,
∴∠CBD=∠EBD,
∵DE∥BC,
∴∠CBD=∠EDB,
∴∠EBD=∠EDB.
(2)解:CD=ED,理由如下:
∵AB=AC,
∴∠C=∠ABC,
∵DE∥BC,
∴∠ADE=∠C,∠AED=∠ABC,
∴∠ADE=∠AED,
∴AD=AE,
∴CD=BE,
由(1)得,∠EBD=∠EDB,
∴BE=DE,
∴CD=ED.
19.解:(1)△CEF是等边三角形,理由如下:
∵△ABC是等边三角形,
∴∠ABC=∠ACB=60°.
∵AB∥DE,
∴∠CEF=∠ABC=60°,
∴∠CEF=∠CFE=∠ECF=60°,
∴△CEF是等边三角形;
(2)∵△ABC是等边三角形,△CEF是等边三角形,
∴AB=BC,CF=CE=4.
∵AD=CD,
∴BD是线段AC的垂直平分线,
∴BD平分∠ABC,
∴∠ABD=∠CBD.
∵AB∥DE,
∴∠ABD=∠BDE,
∴∠BDE=∠CBD,
∴BE=DE.
∵BC=BE+EC=DE+CF,
∴DE=BC﹣CF=10﹣4=6.
20.证明:∵D为AB的中点,
∴AD=BD.
∵DE⊥AC,DF⊥BC,
∴∠AED=∠BFD=90°.
在Rt△ADE和Rt△BDF中,
,
∴Rt△ADE≌Rt△BDF(HL),
∴∠A=∠B,
∴CA=CB,
∵AB=AC,
∴AB=BC=AC
∴△ABC是等边三角形.
21.证明:∵△ABC是等边三角形,
∴AB=AC=BC,∠ABC=∠ACB=∠CAB=60°,
∵DF⊥AB,DE⊥CB,EF⊥AC,
∴∠DAB=∠ACF=∠CBE=90°,
∴∠FAC=∠BCE=∠DBA=30°,
∴∠D=∠E=∠F=180°﹣90°﹣30°=60°,
∴DF=DE=EF,
∴△DEF是等边三角形.
一.选择题(共8小题,满分32分)
1.若等腰三角形的两边长分别为2和5,则它的周长为( )
A.9 B.7 C.12 D.9或12
2.等腰三角形一边长等于2,一边长等于3,则它的周长是( )
A.5 B.7 C.8 D.7或8
3.如图,在直角三角形ABC中,∠ACB=90°,∠B=36°,点D、E在AB上,如果BC=BD,∠CED=∠CDE,那么图中的等腰三角形共有( )个.
A.3个 B.4个 C.5个 D.6个
4.如图,在△ABC中,∠ABC=3∠C,∠1=∠2,BE⊥AE,AB=5,BE=3,则AC=( )
A.10 B.11 C.13 D.15
5.如图,直线l1∥l2,将等边三角形如图放置若∠α=25°,则∠β等于( )
A.35° B.30° C.25° D.20°
6.三角形的三边长a,b,c满足(a﹣b)4+(b﹣c)2+|c﹣a|=0,那么这个三角形一定是( )
A.直角三角形 B.等边三角形
C.等腰非等边三角形 D.钝角三角形
7.如图,△ABC是等边三角形,点E,F分别在AB,AC边上,且EF∥BC,若AB=6,BE=2,则EF的长为( )
A.6 B.4 C.3 D.2
8.在△ABC中,∠C=90°,∠B=30°,AB=6,则AC的长是( )
A. B.3 C.6 D.5
二.填空题(共6小题,满分30分)
9.若等腰三角形的底角为55°,则这个等腰三角形的顶角是 °.
10.在等腰△ABC中,∠A=3∠B,则∠C的度数为 .
11.如图,在△ABC中,边AB的垂直平分线分别交AB、AC于点D,E,若AD为4cm,△ABC的周长为26cm,则△BCE的周长为 cm.
12.如图,一艘船从A处出发向正北航行50海里到达B处,分别从A,B望灯塔C,测得∠NAC=42°,∠NBC=84°,则B处到灯塔C的距离是 海里.
13.已知有一个角为60°的等腰三角形的腰长为4,则这个等腰三角形的周长为 .
14.已知a、b、c是△ABC的三边的长,且满足a2+2b2+c2﹣2b(a+c)=0,则此三角形的形状为 .
三.解答题(共7小题,满分58分)
15.如图,在△ABC中,AB=AC,∠A=2∠ABD,当△BDC是等腰三角形时,求:∠DBC的度数.
16.如图所示,在△ABC中,D是BC上一点,AD=BD,∠C=∠ADC,∠BAC=57°,求∠DAC的度数.
17.已知:如图,在△ABC中,AB=AC,BD与CE相交于点O,且EB=DC.求证:△BOC是等腰三角形.
18.如图,BD是△ABC的角平分线,DE∥BC,交AB于点E.
(1)求证:∠EBD=∠EDB.
(2)当AB=AC时,请判断CD与ED的大小关系,并说明理由.
19.如图,点D在等边△ABC的外部,连接AD、CD,AD=CD,过点D作DE∥AB交AC于点F,交BC于点E.
(1)判断△CEF的形状,并说明理由;
(2)连接BD,若BC=10,CF=4,求DE的长.
20.如图,在△ABC中,AB=AC,D为AB边的中点,DE⊥AC于点E,DF⊥BC于点F,DE=DF.求证:△ABC是等边三角形.
21.如图,△ABC是等边三角形,DF⊥AB,DE⊥CB,EF⊥AC,求证:△DEF是等边三角形.
参考答案
一.选择题(共8小题,满分32分)
1.解:(1)若2为腰长,5为底边长,
由于2+2<5,则三角形不存在;
(2)若5为腰长,则符合三角形的两边之和大于第三边.
所以这个三角形的周长为5+5+2=12.
故选:C.
2.解:分两种情况:
当腰为2时,2+2>3,所以能构成三角形,周长是2+2+3=7;
当腰为3时,3+2>3,所以能构成三角形,周长是:2+3+3=8.
故选:D.
3.解:∵∠ACB=90°,∠B=36°,
∴∠A=54°,
∵BC=BD,
∴∠CDB=∠DCB=72°,
∴∠ECB=36°,∠ACE=54°,
∴CE=BE,AE=CE,
∴△BCD,△CDE,△CEB,△ACE都是等腰三角形,
故选:B.
4.解:延长BE交AC于M,
∵BE⊥AE,
∴∠AEB=∠AEM=90°
∴∠3=90°﹣∠1,∠4=90°﹣∠2,
∵∠1=∠2,
∴∠3=∠4,
∴AB=AM=5,
∵BE⊥AE,
∴BM=2BE=6,
∵∠4是△BCM的外角,
∴∠4=∠5+∠C,
∵∠ABC=3∠C,
∴∠ABC=∠3+∠5=∠4+∠5,
∴3∠C=∠4+∠5=2∠5+∠C,
∴∠5=∠C,
∴CM=BM=6,
∴AC=AM+CM=AB+2BE=11.
故选:B.
5.解:过点B作BD∥l1,如图,
则∠ABD=∠α=25°.
∵l1∥l2,
∴BD∥l2,
∵∠DBC=∠β.
∵△ABC是等边三角形,
∴∠ABC=60°,
∴∠β=∠CBD=∠ABC﹣∠ABD=60°﹣25°=35°.
故选:A.
6.解:∵(a﹣b)4+(b﹣c)2+|c﹣a|=0,
∴a﹣b=0,b﹣c=0,c﹣a=0,
∴a=b=c.
又∵a,b,c是三角形的三边长,
∴这个三角形是等边三角形.
故选:B.
7.解:∵AB=6,BE=2,
∴AE=AB﹣BE=4,
∵△ABC是等边三角形,
∴∠A=∠B=∠C=60°,
∵EF∥BC,
∴∠AEF=∠B=60°,∠AFE=∠C=60°,
∴∠A=∠AEF=∠AFE=60°,
∴△AEF是等边三角形,
∴EF=AE=4.
故选:B.
8.解:∵∠C=90°,∠B=30°,AB=6,
∴AC=AB=×6=3,
故选:B.
二.填空题(共6小题,满分30分)
9.解:如图,在等腰△ABC中,
∵∠B=∠C=55°,∠A+∠B+∠C=180°,
∴∠A=180°﹣∠B﹣∠C,
=180°﹣55°﹣55°,
=70°;
故答案为:70.
10.解:设∠B=x°,则∠A=3x°,
当∠A是顶角时,∠A+2∠B=180°,
即:5x=180,
解得:x=36,
此时∠C=∠B=36°;
当∠A是底角时,∠A=∠C=3x°,
∠A+∠C+∠B=180°,
即7x=180,
解得:x=()°,
此时∠C=3x=()°,
故答案为:36°或()°.
11.解:∵ED垂直平分AB,
∴AE=BE,
∴BD=AD=4cm,AB=8cm,
∵△ABC的周长为26cm,
∴AC+BC=18cm,
△BCE的周长=BC+CE+AE=BC+CE+AE=18cm.
故填18.
12.解:根据题意得:AB=50海里,
∵∠NAC=42°,∠NBC=84°,
∴∠C=∠NBC﹣∠NAC=42°,
∴∠C=∠NAC,
∴BC=AB=50海里.
即从海岛B到灯塔C的距离是50海里.
故答案为:50.
13.解:由题意知,这个三角形为等边三角形,
∴周长为3×4=12,
故答案为:12.
14.解:由已知条件a2+2b2+c2﹣2b(a+c)=0化简得,
(a﹣b)2+(b﹣c)2=0
∴a﹣b=0,b﹣c=0
即 a=b,b=c
∴a=b=c
故答案为等边三角形.
三.解答题(共7小题,满分58分)
15.解:∵AB=AC,
∴∠ABC=∠C.
①当BD=CD时,∠C=∠CBD<∠ABC,故不成立;
②当BD=BC时,∠C=∠BDC=∠A+∠ABD,
∵∠A+∠ABC+∠C=180°,
∴∠A+∠A+∠ABD+∠A+∠ABD=180°,
∴3∠A+2∠ABD=180°,4∠A=180°,
∴∠A=45°,
∴∠ABD=22.5°,
∴∠ABC=(180°﹣45°)=67.5°,
∴∠DBC=∠ABC﹣∠ACD=45°;
③当CB=CD时,∠CBD=∠CDB=∠A+∠ABD,
设∠ABD=x,
∴∠A=2x,
∴∠CBD=∠CDB=3x,
∴∠ABC=∠C=4x,
∵∠A+∠ABC+∠C=180°,
∴2x+4x+4x=180°,
∴x=18°,
∴∠DBC=54°;
综上所述:∠DBC的度数为54°或45°.
16.解:∵AD=BD,
∴∠B=∠BAD,
∵∠ADC=∠B+∠BAD=2∠B,
∴∠C=2∠B,
∵∠BAC=57°,
∴∠B+∠C=3∠B=180°﹣∠BAC=41°,
∴∠ADC=∠C=82°,
∴∠DAC=16°.
17.证明:∵AB=AC,
∴∠ABC=∠ACB,
在△BEC与△CDB 中,
,
∴△BEC≌△CDB(SAS),
∴∠OCB=∠OBC,
∴OB=OC,
∴△BOC是等腰三角形.
18.(1)证明:∵BD是△ABC的角平分线,
∴∠CBD=∠EBD,
∵DE∥BC,
∴∠CBD=∠EDB,
∴∠EBD=∠EDB.
(2)解:CD=ED,理由如下:
∵AB=AC,
∴∠C=∠ABC,
∵DE∥BC,
∴∠ADE=∠C,∠AED=∠ABC,
∴∠ADE=∠AED,
∴AD=AE,
∴CD=BE,
由(1)得,∠EBD=∠EDB,
∴BE=DE,
∴CD=ED.
19.解:(1)△CEF是等边三角形,理由如下:
∵△ABC是等边三角形,
∴∠ABC=∠ACB=60°.
∵AB∥DE,
∴∠CEF=∠ABC=60°,
∴∠CEF=∠CFE=∠ECF=60°,
∴△CEF是等边三角形;
(2)∵△ABC是等边三角形,△CEF是等边三角形,
∴AB=BC,CF=CE=4.
∵AD=CD,
∴BD是线段AC的垂直平分线,
∴BD平分∠ABC,
∴∠ABD=∠CBD.
∵AB∥DE,
∴∠ABD=∠BDE,
∴∠BDE=∠CBD,
∴BE=DE.
∵BC=BE+EC=DE+CF,
∴DE=BC﹣CF=10﹣4=6.
20.证明:∵D为AB的中点,
∴AD=BD.
∵DE⊥AC,DF⊥BC,
∴∠AED=∠BFD=90°.
在Rt△ADE和Rt△BDF中,
,
∴Rt△ADE≌Rt△BDF(HL),
∴∠A=∠B,
∴CA=CB,
∵AB=AC,
∴AB=BC=AC
∴△ABC是等边三角形.
21.证明:∵△ABC是等边三角形,
∴AB=AC=BC,∠ABC=∠ACB=∠CAB=60°,
∵DF⊥AB,DE⊥CB,EF⊥AC,
∴∠DAB=∠ACF=∠CBE=90°,
∴∠FAC=∠BCE=∠DBA=30°,
∴∠D=∠E=∠F=180°﹣90°﹣30°=60°,
∴DF=DE=EF,
∴△DEF是等边三角形.
