人教2022版数学六年级上册第八单元易错题专项练习-填空题(含答案)
文档属性
| 名称 | 人教2022版数学六年级上册第八单元易错题专项练习-填空题(含答案) |

|
|
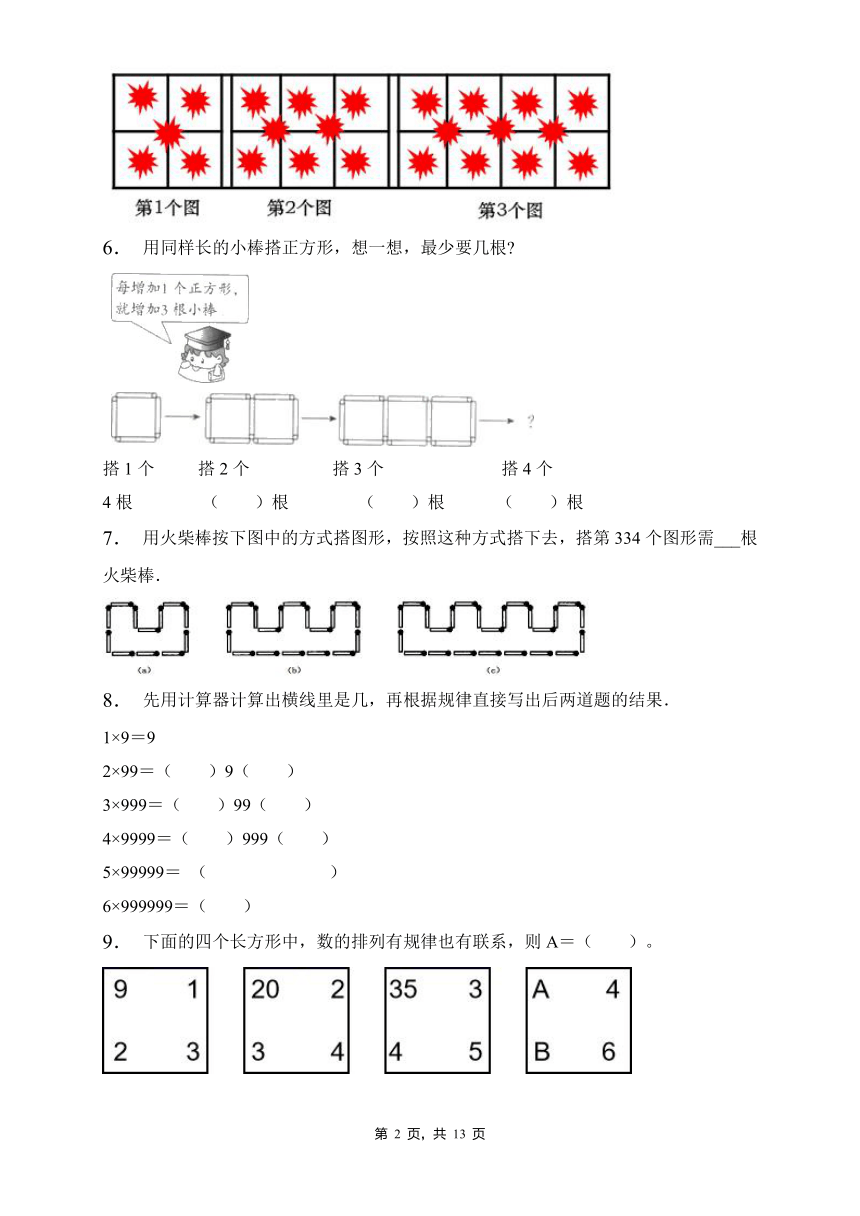
| 格式 | doc | ||
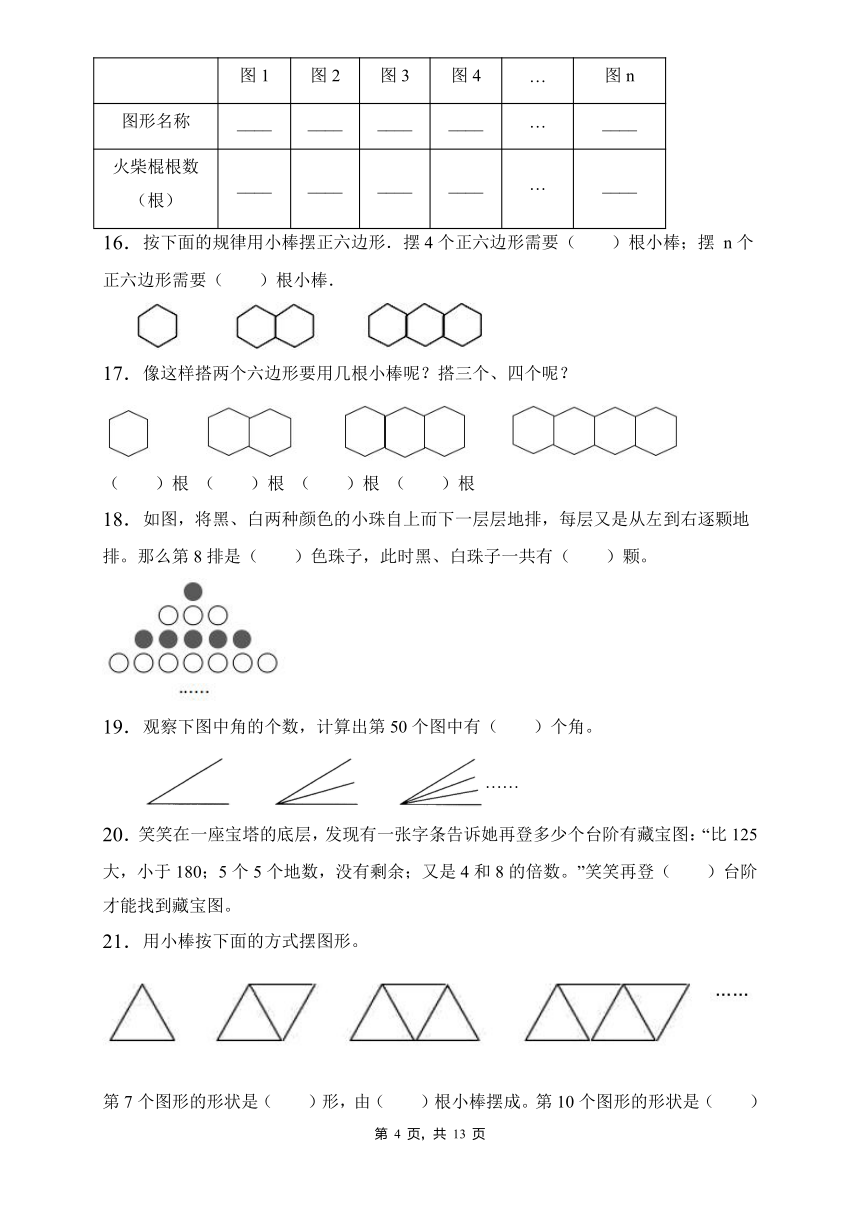
| 文件大小 | 698.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-10 07:00:25 | ||
图片预览


文档简介
人教版数学六年级上册第八单元易错题专项训练
填空题
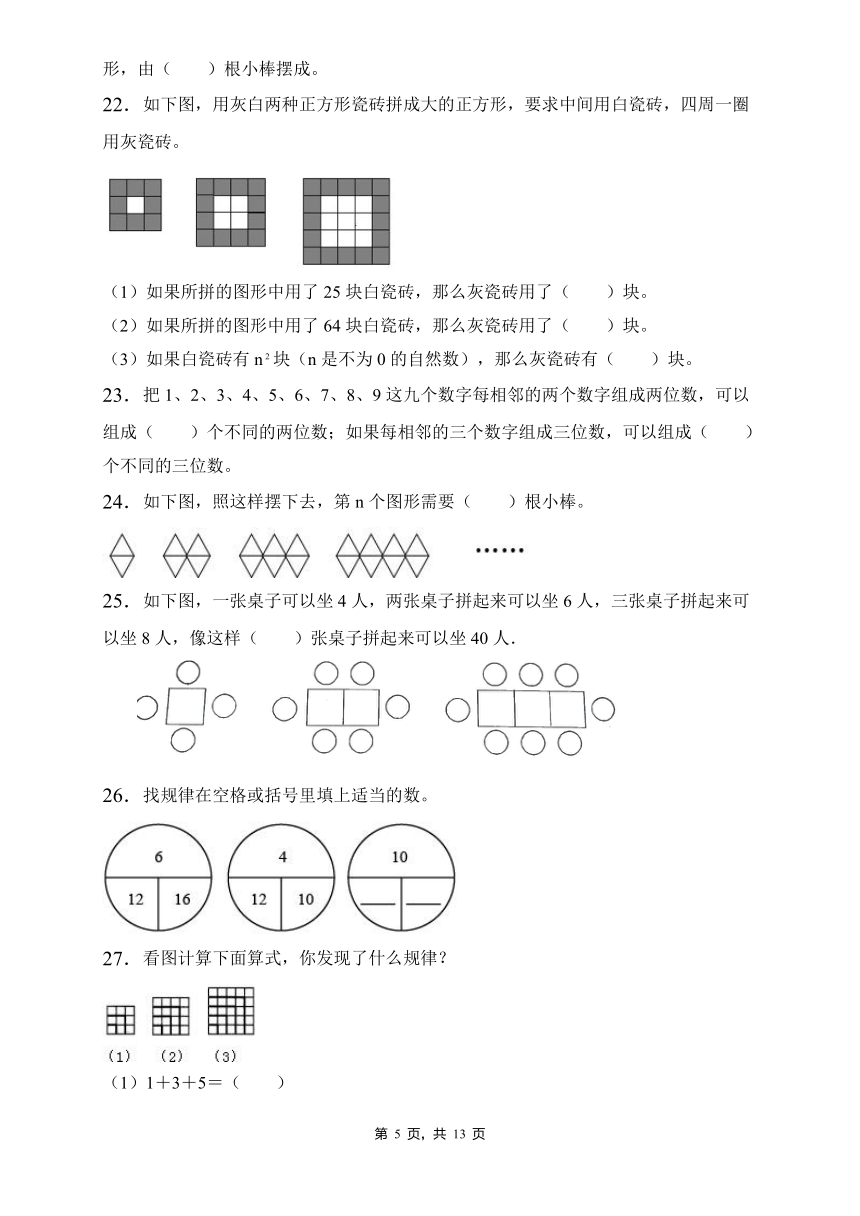
一、 认真审题,弄清题意,突破难点,夯实基础。
1. 如下图,画2个正方形能得到4个直角三角形,画3个正方形能得到8个直角三角形,画10个正方形能得到( )个直角三角形。
2. 把同样大小的圆圈按如图所示的方式摆放,第10个图形需要( )个小圆圈。
3. 观察下图,第7幅图有( )个棋子,第15幅图有( )个棋子,第n幅图有( )个棋子。
4. 如图,小三角形的边长是1cm,第五个图形的周长是( )cm.
5. 小明在社会大课堂的研学活动中,发现中式建筑中的窗格
图案很多都是有规律排列的.第一个图案上有5个“”,第二个图案上有8个“”,如果按照下面的样子画下去,第四个图案上有( )个“”,第n个图案上有( )个“”.
6. 用同样长的小棒搭正方形,想一想,最少要几根
搭1个 搭2个 搭3个 搭4个
4根 ( )根 ( )根 ( )根
7. 用火柴棒按下图中的方式搭图形,按照这种方式搭下去,搭第334个图形需___根火柴棒.
8. 先用计算器计算出横线里是几,再根据规律直接写出后两道题的结果.
1×9=9
2×99=( )9( )
3×999=( )99( )
4×9999=( )999( )
5×99999= ( )
6×999999=( )
9. 下面的四个长方形中,数的排列有规律也有联系,则A=( )。
10.
上图中,摆一个正方形用了4根,摆两个正方形用了( )根,像这样摆3个正方形一共要用( )根。
11.用小棒摆图形,按照这样的规律摆下去,第4个图形用了( )根,第10个图形用了( )根,第( )个图形用了98根。
12.用同样大小的黑色棋子按下图所示的方式摆图形,按照这样的规律摆下去,则第n个图形需棋子( )枚(用含n的代数式表示)。
…
第1个图 第2个图 第3个图
13.找规律填数:图中正方形表示桌子,圆圈表示椅子.25张桌子可以坐( )人.
14.学校阅览室有能坐4人的方桌,如果多于4人,就把方桌拼成一行,2张方桌拼成一行能坐6人(如图所示),请你结合这个规律,填写下表:
方桌数 1张 2张 3张 4张 n张
人数 ( ) ( ) ( ) ( ) ( )
15.找规律填表。
图1 图2 图3 图4 … 图n
图形名称 ____ ____ ____ ____ … ____
火柴棍根数(根) ____ ____ ____ ____ … ____
16.按下面的规律用小棒摆正六边形.摆4个正六边形需要( )根小棒;摆 n个正六边形需要( )根小棒.
17.像这样搭两个六边形要用几根小棒呢?搭三个、四个呢?
( )根 ( )根 ( )根 ( )根
18.如图,将黑、白两种颜色的小珠自上而下一层层地排,每层又是从左到右逐颗地排。那么第8排是( )色珠子,此时黑、白珠子一共有( )颗。
19.观察下图中角的个数,计算出第50个图中有( )个角。
……
20.笑笑在一座宝塔的底层,发现有一张字条告诉她再登多少个台阶有藏宝图:“比125大,小于180;5个5个地数,没有剩余;又是4和8的倍数。”笑笑再登( )台阶才能找到藏宝图。
21.用小棒按下面的方式摆图形。
第7个图形的形状是( )形,由( )根小棒摆成。第10个图形的形状是( )形,由( )根小棒摆成。
22.如下图,用灰白两种正方形瓷砖拼成大的正方形,要求中间用白瓷砖,四周一圈用灰瓷砖。
(1)如果所拼的图形中用了25块白瓷砖,那么灰瓷砖用了( )块。
(2)如果所拼的图形中用了64块白瓷砖,那么灰瓷砖用了( )块。
(3)如果白瓷砖有n块(n是不为0的自然数),那么灰瓷砖有( )块。
23.把1、2、3、4、5、6、7、8、9这九个数字每相邻的两个数字组成两位数,可以组成( )个不同的两位数;如果每相邻的三个数字组成三位数,可以组成( )个不同的三位数。
24.如下图,照这样摆下去,第n个图形需要( )根小棒。
25.如下图,一张桌子可以坐4人,两张桌子拼起来可以坐6人,三张桌子拼起来可以坐8人,像这样( )张桌子拼起来可以坐40人.
26.找规律在空格或括号里填上适当的数。
27.看图计算下面算式,你发现了什么规律?
(1)1+3+5=( )
(2)1+3+5+7=( )
(3)1+3+5+7+9=( )
规律:( )( )_。
28.有5个黑色和白色棋子围成一圈,规定:将同色且相邻的两个棋子之间放入一个白色棋子,在异色且相邻的两个棋子之间放入一个黑色棋子,然后将原来的5个棋子拿掉.如果第一幅图的初始状态开始依照上述规定操作下去,对于圆圈上呈现5个棋子的情况,圆圈上黑子最多能有( )个.
29.数一数,图中大小正方体的个数。单位:厘米
棱长: ( ) ( )
正方体个数13+23 =( ) 13+23 +33=( )
如果正方体的棱长是4,那么大小正方体的个数是( )个。
30.找规律,下列图中有大小相同的菱形,第1幅图中有1个菱形,第2幅图中有3个菱形,第3幅图中有5个菱形,则第4幅图中有____个菱形,第n幅图中有( )个菱形。
1 2 3 n
31.找规律,填一填。
①0.2、0.6、1.8、( )、16.2、( )、( )。
②0.1、0.2、0.3、0.5、0.8、( )、2.1、( )。
32.小明今年11岁,属相是 “猴”,小明的姑姑比他大一轮,小明姑姑今年( )岁;妈妈比小明大两轮,小明妈妈今年( )岁。
33.按这样的方式摆下去,摆4个连着的正六边形需要( )根小棒,摆个连着的正六边形需要( )根小棒。
……
34.找规律写得数。
1.2×9=10.8 1.23×9=11.07
1.234×9=11.106 1.2345×9=11.1105
1.23456×9=( ) 1.234567×9=( )
1.2345678×9=( ) 1.23456789×9=( )
35.如图所示,用白色和灰色小正方形按如图的规律摆大正方形。照这样接着摆下去,第6幅图一共有( )个白色小正方形。
36.把一根绳对折1次,得到2段,且有一个折痕;再对折1次,得到4段,且有3个折痕,如此下去,对折5次后,得到( )段,且有( )个折痕。
37.下图都是由同样大小的五角星按一定的规律组成的,其中第①个图形中一共有2个五角星,第②个图形中一共有8个五角星,第③个图形中一共有18个五角星,……,则第⑤个图形中五角星为( ) 个。
38.按下面的规律铺瓷砖第28幅图中应铺( )块黑色瓷砖。
39.拿出一张正三角形,将它按如下图形状折叠,展开后沿折痕剪开,就剪出了四个小正方形,我们把这称为第一次操作;再拿出其中一个小正三角形,将它同样也剪成四个小三角形,我们把它称作第二次操作;再拿出其中一个小正三角形,将它同样也剪成四个小三角形,我们把它称作第三次操作……
(1)根据操作情况完成下表:
操作的次 最初 第一次 第二次 第三次 第四次
共有正三角形的个 1 4 ( ) ( ) ( )
(2)假设这个操作可以一直继续下去,那么n次操作后,一共有( )个正三角形。
(3)第( )次操作后,一共剪出了70个正三角形。
40.用小棒按照如下的方式摆图形.
(1)摆一个六边形需要6根小棒,摆2个六边形需要11根小棒,摆三个六边形需要( )根小棒;
(2)照这样摆下去:摆n个六边形需要( )根小棒,但n=60时,需要( )根小棒.
41.有一个正六边形点阵,如图,它的中心是一个点,算作第一层,第二层每边2个点,第三层每边3个点,…这个六边形点阵第28层上面共有( )个点,第100层( )个点.
42.观察下面的点阵图,按规律填一填。
第4个点阵图中的点子数:( )+( )+( )=( )
第8个点阵图中的点子数:( )+( )+( )=( )
第n个点阵图中的点子数:( )+( )+( )=( )
第( )个点阵图中有300个点子。
43.搭建如图(1)的单顶帐篷需要17根钢管,若这样的帐篷按图(2)、图(3)的方式串起来搭建,则可节省结合处的钢管,那么串搭20顶这样的帐篷需要( )根钢管。
44.随着三角形个数的增加,涂色三角形的个数也地增加,照这样接下去画,第10个图形中会有( )个涂色的三角形。
45.先计算前三题,再根据发现的规律直接写出其他算式的结果.
1+3═( )=22
1+3+5═( )=32
1+3+5+7═( )=____
…
1+3+5+7+…+15═( )=____
1+3+5+7+…+2017=( )=____
46.如图,一张桌子可坐4人,两张桌子可坐6人。像这样( )张桌子拼起来可坐40人。
47.如下图,用同样大小的黑、白两种颜色的棋子摆设如下图所示的正方形图案,则第n个图案需要用白色棋子( )枚(用含有n的代数式表示,并写成最简形式)。
48.四边形、五边形、六边形……从一个顶点出发可以把这些图形分成若干个三角形,根据你的发现,七边形从一点出发可以分成( )个三角形,九边形从一点出发可以分成( )个三角形。
49.数形结合是一种重要的数学思想,认真观察图形,然后完成下列问题。
1+3=4=22
1+3+5=9=32
1+3+5+7=( )=( )2
1+3+5+7+9=( )2
1+3+5+7+…=(2n-1)=( )2
50.如图,观察图形的规律,第8个图形一共由( )个小三角形组成.
(参考答案)
一、 认真审题,弄清题意,突破难点,夯实基础。
1. 36
2. 100
3. 49 225 n2
4. 7
5. 14 3n+2
6. 7 10 13
7. 2010
8. 1 8 2 7 3 6 499995 5999994
9. 54
10.7 10
11.18 42 24
12.3n+1
13.102
14.4 6 8 10 2n+2
15.三角形 平行四边形 梯形 平行四边形 三角形或梯形或平行四边形 3 5 7 9 2n+1
16.21 5n+1
17.6 11 16 21
18.白 64
19.1275
20.160个
21.梯形 15 平行四边形 21
22.24 36 4n+4
23.16 42
24.5n
25.19
26.
27.9,即32 16,即42; 25,即52 从1开始的连续几个奇数相加,即数的个数的平方
28.4个
29.2 3 9 36 100
30.7 2n-1
31.5.4 48.6 145.8 1.3 3.4
32.23 35
33.21 5n+1
34.11.11104 11.111103 11.1111102 11.11111101
35.14
36.32 31
37.50
38.85
39.7 10 13 3n+1 23
40.16 (5n+1) 301
41.162 594
42.4 5 6 15 8 9 10 27 n n+1 n+2 3n+3 99
43.226
44.55
45.4 9 16 42 64 82 1018081 10092
46.19张
47.4n+4
48.5 7
49.16 42 52 n2
50.64
1
第 1 页,共 1 页
填空题
一、 认真审题,弄清题意,突破难点,夯实基础。
1. 如下图,画2个正方形能得到4个直角三角形,画3个正方形能得到8个直角三角形,画10个正方形能得到( )个直角三角形。
2. 把同样大小的圆圈按如图所示的方式摆放,第10个图形需要( )个小圆圈。
3. 观察下图,第7幅图有( )个棋子,第15幅图有( )个棋子,第n幅图有( )个棋子。
4. 如图,小三角形的边长是1cm,第五个图形的周长是( )cm.
5. 小明在社会大课堂的研学活动中,发现中式建筑中的窗格
图案很多都是有规律排列的.第一个图案上有5个“”,第二个图案上有8个“”,如果按照下面的样子画下去,第四个图案上有( )个“”,第n个图案上有( )个“”.
6. 用同样长的小棒搭正方形,想一想,最少要几根
搭1个 搭2个 搭3个 搭4个
4根 ( )根 ( )根 ( )根
7. 用火柴棒按下图中的方式搭图形,按照这种方式搭下去,搭第334个图形需___根火柴棒.
8. 先用计算器计算出横线里是几,再根据规律直接写出后两道题的结果.
1×9=9
2×99=( )9( )
3×999=( )99( )
4×9999=( )999( )
5×99999= ( )
6×999999=( )
9. 下面的四个长方形中,数的排列有规律也有联系,则A=( )。
10.
上图中,摆一个正方形用了4根,摆两个正方形用了( )根,像这样摆3个正方形一共要用( )根。
11.用小棒摆图形,按照这样的规律摆下去,第4个图形用了( )根,第10个图形用了( )根,第( )个图形用了98根。
12.用同样大小的黑色棋子按下图所示的方式摆图形,按照这样的规律摆下去,则第n个图形需棋子( )枚(用含n的代数式表示)。
…
第1个图 第2个图 第3个图
13.找规律填数:图中正方形表示桌子,圆圈表示椅子.25张桌子可以坐( )人.
14.学校阅览室有能坐4人的方桌,如果多于4人,就把方桌拼成一行,2张方桌拼成一行能坐6人(如图所示),请你结合这个规律,填写下表:
方桌数 1张 2张 3张 4张 n张
人数 ( ) ( ) ( ) ( ) ( )
15.找规律填表。
图1 图2 图3 图4 … 图n
图形名称 ____ ____ ____ ____ … ____
火柴棍根数(根) ____ ____ ____ ____ … ____
16.按下面的规律用小棒摆正六边形.摆4个正六边形需要( )根小棒;摆 n个正六边形需要( )根小棒.
17.像这样搭两个六边形要用几根小棒呢?搭三个、四个呢?
( )根 ( )根 ( )根 ( )根
18.如图,将黑、白两种颜色的小珠自上而下一层层地排,每层又是从左到右逐颗地排。那么第8排是( )色珠子,此时黑、白珠子一共有( )颗。
19.观察下图中角的个数,计算出第50个图中有( )个角。
……
20.笑笑在一座宝塔的底层,发现有一张字条告诉她再登多少个台阶有藏宝图:“比125大,小于180;5个5个地数,没有剩余;又是4和8的倍数。”笑笑再登( )台阶才能找到藏宝图。
21.用小棒按下面的方式摆图形。
第7个图形的形状是( )形,由( )根小棒摆成。第10个图形的形状是( )形,由( )根小棒摆成。
22.如下图,用灰白两种正方形瓷砖拼成大的正方形,要求中间用白瓷砖,四周一圈用灰瓷砖。
(1)如果所拼的图形中用了25块白瓷砖,那么灰瓷砖用了( )块。
(2)如果所拼的图形中用了64块白瓷砖,那么灰瓷砖用了( )块。
(3)如果白瓷砖有n块(n是不为0的自然数),那么灰瓷砖有( )块。
23.把1、2、3、4、5、6、7、8、9这九个数字每相邻的两个数字组成两位数,可以组成( )个不同的两位数;如果每相邻的三个数字组成三位数,可以组成( )个不同的三位数。
24.如下图,照这样摆下去,第n个图形需要( )根小棒。
25.如下图,一张桌子可以坐4人,两张桌子拼起来可以坐6人,三张桌子拼起来可以坐8人,像这样( )张桌子拼起来可以坐40人.
26.找规律在空格或括号里填上适当的数。
27.看图计算下面算式,你发现了什么规律?
(1)1+3+5=( )
(2)1+3+5+7=( )
(3)1+3+5+7+9=( )
规律:( )( )_。
28.有5个黑色和白色棋子围成一圈,规定:将同色且相邻的两个棋子之间放入一个白色棋子,在异色且相邻的两个棋子之间放入一个黑色棋子,然后将原来的5个棋子拿掉.如果第一幅图的初始状态开始依照上述规定操作下去,对于圆圈上呈现5个棋子的情况,圆圈上黑子最多能有( )个.
29.数一数,图中大小正方体的个数。单位:厘米
棱长: ( ) ( )
正方体个数13+23 =( ) 13+23 +33=( )
如果正方体的棱长是4,那么大小正方体的个数是( )个。
30.找规律,下列图中有大小相同的菱形,第1幅图中有1个菱形,第2幅图中有3个菱形,第3幅图中有5个菱形,则第4幅图中有____个菱形,第n幅图中有( )个菱形。
1 2 3 n
31.找规律,填一填。
①0.2、0.6、1.8、( )、16.2、( )、( )。
②0.1、0.2、0.3、0.5、0.8、( )、2.1、( )。
32.小明今年11岁,属相是 “猴”,小明的姑姑比他大一轮,小明姑姑今年( )岁;妈妈比小明大两轮,小明妈妈今年( )岁。
33.按这样的方式摆下去,摆4个连着的正六边形需要( )根小棒,摆个连着的正六边形需要( )根小棒。
……
34.找规律写得数。
1.2×9=10.8 1.23×9=11.07
1.234×9=11.106 1.2345×9=11.1105
1.23456×9=( ) 1.234567×9=( )
1.2345678×9=( ) 1.23456789×9=( )
35.如图所示,用白色和灰色小正方形按如图的规律摆大正方形。照这样接着摆下去,第6幅图一共有( )个白色小正方形。
36.把一根绳对折1次,得到2段,且有一个折痕;再对折1次,得到4段,且有3个折痕,如此下去,对折5次后,得到( )段,且有( )个折痕。
37.下图都是由同样大小的五角星按一定的规律组成的,其中第①个图形中一共有2个五角星,第②个图形中一共有8个五角星,第③个图形中一共有18个五角星,……,则第⑤个图形中五角星为( ) 个。
38.按下面的规律铺瓷砖第28幅图中应铺( )块黑色瓷砖。
39.拿出一张正三角形,将它按如下图形状折叠,展开后沿折痕剪开,就剪出了四个小正方形,我们把这称为第一次操作;再拿出其中一个小正三角形,将它同样也剪成四个小三角形,我们把它称作第二次操作;再拿出其中一个小正三角形,将它同样也剪成四个小三角形,我们把它称作第三次操作……
(1)根据操作情况完成下表:
操作的次 最初 第一次 第二次 第三次 第四次
共有正三角形的个 1 4 ( ) ( ) ( )
(2)假设这个操作可以一直继续下去,那么n次操作后,一共有( )个正三角形。
(3)第( )次操作后,一共剪出了70个正三角形。
40.用小棒按照如下的方式摆图形.
(1)摆一个六边形需要6根小棒,摆2个六边形需要11根小棒,摆三个六边形需要( )根小棒;
(2)照这样摆下去:摆n个六边形需要( )根小棒,但n=60时,需要( )根小棒.
41.有一个正六边形点阵,如图,它的中心是一个点,算作第一层,第二层每边2个点,第三层每边3个点,…这个六边形点阵第28层上面共有( )个点,第100层( )个点.
42.观察下面的点阵图,按规律填一填。
第4个点阵图中的点子数:( )+( )+( )=( )
第8个点阵图中的点子数:( )+( )+( )=( )
第n个点阵图中的点子数:( )+( )+( )=( )
第( )个点阵图中有300个点子。
43.搭建如图(1)的单顶帐篷需要17根钢管,若这样的帐篷按图(2)、图(3)的方式串起来搭建,则可节省结合处的钢管,那么串搭20顶这样的帐篷需要( )根钢管。
44.随着三角形个数的增加,涂色三角形的个数也地增加,照这样接下去画,第10个图形中会有( )个涂色的三角形。
45.先计算前三题,再根据发现的规律直接写出其他算式的结果.
1+3═( )=22
1+3+5═( )=32
1+3+5+7═( )=____
…
1+3+5+7+…+15═( )=____
1+3+5+7+…+2017=( )=____
46.如图,一张桌子可坐4人,两张桌子可坐6人。像这样( )张桌子拼起来可坐40人。
47.如下图,用同样大小的黑、白两种颜色的棋子摆设如下图所示的正方形图案,则第n个图案需要用白色棋子( )枚(用含有n的代数式表示,并写成最简形式)。
48.四边形、五边形、六边形……从一个顶点出发可以把这些图形分成若干个三角形,根据你的发现,七边形从一点出发可以分成( )个三角形,九边形从一点出发可以分成( )个三角形。
49.数形结合是一种重要的数学思想,认真观察图形,然后完成下列问题。
1+3=4=22
1+3+5=9=32
1+3+5+7=( )=( )2
1+3+5+7+9=( )2
1+3+5+7+…=(2n-1)=( )2
50.如图,观察图形的规律,第8个图形一共由( )个小三角形组成.
(参考答案)
一、 认真审题,弄清题意,突破难点,夯实基础。
1. 36
2. 100
3. 49 225 n2
4. 7
5. 14 3n+2
6. 7 10 13
7. 2010
8. 1 8 2 7 3 6 499995 5999994
9. 54
10.7 10
11.18 42 24
12.3n+1
13.102
14.4 6 8 10 2n+2
15.三角形 平行四边形 梯形 平行四边形 三角形或梯形或平行四边形 3 5 7 9 2n+1
16.21 5n+1
17.6 11 16 21
18.白 64
19.1275
20.160个
21.梯形 15 平行四边形 21
22.24 36 4n+4
23.16 42
24.5n
25.19
26.
27.9,即32 16,即42; 25,即52 从1开始的连续几个奇数相加,即数的个数的平方
28.4个
29.2 3 9 36 100
30.7 2n-1
31.5.4 48.6 145.8 1.3 3.4
32.23 35
33.21 5n+1
34.11.11104 11.111103 11.1111102 11.11111101
35.14
36.32 31
37.50
38.85
39.7 10 13 3n+1 23
40.16 (5n+1) 301
41.162 594
42.4 5 6 15 8 9 10 27 n n+1 n+2 3n+3 99
43.226
44.55
45.4 9 16 42 64 82 1018081 10092
46.19张
47.4n+4
48.5 7
49.16 42 52 n2
50.64
1
第 1 页,共 1 页
