沪科版八年级数学上册11.1平面内点的坐标 一课一练(含答案)
文档属性
| 名称 | 沪科版八年级数学上册11.1平面内点的坐标 一课一练(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 81.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-10 00:00:00 | ||
图片预览



文档简介
11.1平面内点的坐标
一、选择题
1.若电影院中“5排8号”的位置,记作(5,8),丽丽的电影票是“3排1号”.则下列有序数对表示丽丽在电影院位置正确的是( )
A.(3,1) B.(1,3) C.(13,31) D.(31,13)
2.若(1,2)表示教室里第1列第2排的位置,则教室里第3列第2排的位置表示为( )
A.(2,3) B.(3,2) C.(2,1) D.(3,3)
3.平面直角坐标系中,点A(﹣2,1)到x轴的距离为( )
A.﹣2 B.1 C.2 D.
4.如果点A(3,m)在x轴上,那么点B(m+2,m﹣3)所在的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
5.若xy>0,则关于点P(x,y)的说法正确的是( )
A.在一或二象限 B.在一或四象限
C.在二或四象限 D.在一或三象限
6.以下说法正确的有( )个
(1)(﹣2019,2019)在第三象限;
(2)(﹣2,3)到x轴的距离是3;
(3)A(2x﹣4,x+2)在x轴上,则x的值是2;
(4)(﹣3,0)在y轴的负半轴上.
A.0 B.1 C.2 D.3
7.已知点P(a﹣5,a+1)在y轴上,则a的值为( )
A.1 B.﹣1 C.﹣5 D.5
8.在平面直角坐标系中,下列说法正确的是( )
A.点P(3,2)到x轴的距离是3
B.若ab=0,则点P(a,b)表示原点
C.若A(2,﹣2)、B(2,2),则直线AB∥x轴
D.第三象限内点的坐标,横纵坐标同号
9.已知点A的坐标为(﹣1,2),直线AB∥x轴,并且AB=4,则点B的坐标为( )
A.(﹣1,6) B.(﹣1,6)或(﹣1,﹣2)
C.(3,2) D.(3,2)或(﹣5,2)
10.如图所示,直角坐标系中四边形的面积是( )
A.15.5 B.20.5 C.26 D.31
二、填空题
11.某会场座位号将“7排4号”记作(7,4),那么“3排5号”记作 .
12.如图,在中国象棋的残局上建立平面直角坐标系,如果“相”的坐标是(4,1),那么“帅”的坐标为 .
13.已知点M(m+1,m+3)在x轴上,则m等于 .
14.如果点P在x轴下方,到x轴的距离是5,到y轴的距离是2,那么点P的坐标为 .
15.在平面直角坐标系中,点P(m,n)在第二象限,则点Q(﹣m+1,n)在第 象限.
16.在平面直角坐标系中,第二象限内有一点M,点M到x轴的距离为5,到y轴的距离为4,则点M的坐标是 .
17.如果点P(x,y)的坐标满足x+y=xy,那么称点P为“和谐点”,若某个“和谐点”到x轴的距离为3,则P点的坐标为 .
18.已知线段AB∥y轴,若点A的坐标为(5,n﹣1),B(n2+1,1),则n为 .
三、解答题
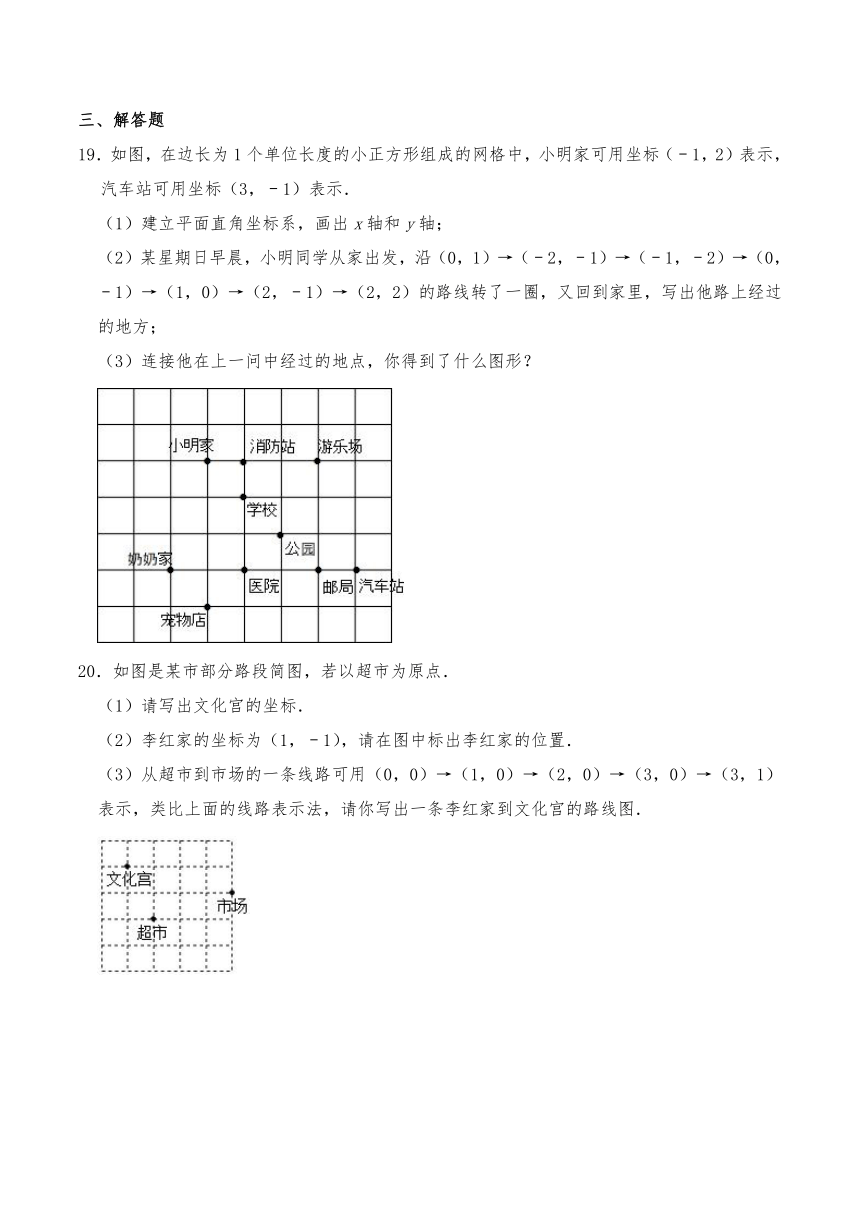
19.如图,在边长为1个单位长度的小正方形组成的网格中,小明家可用坐标(﹣1,2)表示,汽车站可用坐标(3,﹣1)表示.
(1)建立平面直角坐标系,画出x轴和y轴;
(2)某星期日早晨,小明同学从家出发,沿(0,1)→(﹣2,﹣1)→(﹣1,﹣2)→(0,﹣1)→(1,0)→(2,﹣1)→(2,2)的路线转了一圈,又回到家里,写出他路上经过的地方;
(3)连接他在上一问中经过的地点,你得到了什么图形?
20.如图是某市部分路段简图,若以超市为原点.
(1)请写出文化宫的坐标.
(2)李红家的坐标为(1,﹣1),请在图中标出李红家的位置.
(3)从超市到市场的一条线路可用(0,0)→(1,0)→(2,0)→(3,0)→(3,1)表示,类比上面的线路表示法,请你写出一条李红家到文化宫的路线图.
21.已知点P(2x﹣6,3x+1),求下列情形下点P的坐标.
(1)点P在y轴上;
(2)点P到x轴、y轴的距离相等,且点P在第二象限;
(3)点P在过点A(2,﹣4)且与y轴平行的直线上.
22.国庆假期期间,笑笑所在的学习小组组织了到方特梦幻王国的游园活动,笑笑和乐乐对着景区示意图(如图所示)讨论景点位置:(图中小正方形边长代表100m)
笑笑说:“西游传说坐标(300,300).”
乐乐说:“华夏五千年坐标(﹣100,﹣400).”
若他们二人所说的位置都正确
(1)在图中建立适当的平面直角坐标系xOy;
(2)用坐标描述其他地点的位置.
23.已知M(3|a|﹣9,4﹣2a)在y轴负半轴上,直线MN∥x轴,且线段MN长度为4.
(1)求点M的坐标;
(2)求(2﹣a)2020+1的值;
(3)求N点坐标.
24.点P是平面直角坐标系中的一点且不在坐标轴上,过点P向x轴、y轴作垂线段,若垂线段的长度的和为4,则点P叫做“垂距点”,例如:如图中的点P(1,3)是“垂距点”.
(1)在点A(﹣2,2),B(,),C(﹣1,5)中,“垂距点”是 ;
(2)若D(m,m)是“垂距点”,求m的值.
答案
一、选择题
A.B.B.D.D.B.D.D.D.A.
二、填空题
11.(3,5).
12.(0,﹣1).
13.﹣3..
14.(2,﹣5)或(﹣2,﹣5).
15.四.
16.(﹣4,5).
17.(,3)或(,﹣3).
18.﹣2.
三、解答题
19.(1)如图,建立平面直角坐标系;
(2)小明家﹣学校﹣奶奶家﹣宠物店﹣医院﹣公园﹣邮局﹣游乐场﹣消防站﹣小明家;
(3)连接他在上一问中经过的地点,得到“箭头”状的图形.
20.(1)以超市为原点,横坐标向右为正,向左为负,纵坐标向上为正,向下为负,可得文化宫的坐标为:(﹣1,2).
(2)李红家的坐标为(1,﹣1),在图中标出李红家的位置如下:
(3)一条李红家到文化宫的路线图如下:(1,﹣1)→(1,0)→(1,1)→(1,2)→(0,2)→(﹣1,2).
21.(1)∵点P(2x﹣6,3x+1),且点P在y轴上,
∴2x﹣6=0,
∴x=3,
∴3x+1=10,
∴点P的坐标为(0,10);
(2)∵点P(2x﹣6,3x+1),点P到x轴、y轴的距离相等,且点P在第二象限,
∴2x﹣6=﹣(3x+1),
∴2x﹣6+3x+1=0,
∴x=1,
∴2x﹣6=﹣4,3x+1=4,
∴点P的坐标为(﹣4,4);
(3)∵点P(2x﹣6,3x+1)在过点A(2,﹣4)且与y轴平行的直线上,
∴2x﹣6=2,
∴x=4,
∴3x+1=13,
∴点P的坐标为(2,13).
22.(1)如图所示:
(2)太空飞梭(0,0),秦岭历险(0,400),魔幻城堡(400,﹣200),南门(0,﹣500),丛林飞龙(﹣200,﹣100).
23.(1)∵M在y轴负半轴上,
∴3|a|﹣9=0,且4﹣2a<0,
∴a=±3,且a>2,
∴a=3.
∴4﹣2a=﹣2,
M(0,﹣2);
(2)∵a=3,
∴(2﹣a)2020+1
=(2﹣3)2020+1
=1+1
=2;
(3)∵直线MN∥x轴,M(0,﹣2),
∴设N(x,﹣2),
又∵线段MN长度为4,
∴MN=|x﹣0|=|x|=4,
∴x=±4,
∴N(4,﹣2)或(﹣4,﹣2).
24.(1)根据题意,对于点A而言,|﹣2|+|2|=4,
所以A是“垂距点”,
对于点B而言,||+||=3,
所以B不是“垂距点”,
对于点C而言,|﹣1|+|5|=6≠4,
所以C不是“垂距点”,
故答案为:A.
(2)由题意可知:,
①当m>0时,则4m=4,
解得m=1;
②当m<0时,则﹣4m=4,
解得m=﹣1;
∴m=±1.
一、选择题
1.若电影院中“5排8号”的位置,记作(5,8),丽丽的电影票是“3排1号”.则下列有序数对表示丽丽在电影院位置正确的是( )
A.(3,1) B.(1,3) C.(13,31) D.(31,13)
2.若(1,2)表示教室里第1列第2排的位置,则教室里第3列第2排的位置表示为( )
A.(2,3) B.(3,2) C.(2,1) D.(3,3)
3.平面直角坐标系中,点A(﹣2,1)到x轴的距离为( )
A.﹣2 B.1 C.2 D.
4.如果点A(3,m)在x轴上,那么点B(m+2,m﹣3)所在的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
5.若xy>0,则关于点P(x,y)的说法正确的是( )
A.在一或二象限 B.在一或四象限
C.在二或四象限 D.在一或三象限
6.以下说法正确的有( )个
(1)(﹣2019,2019)在第三象限;
(2)(﹣2,3)到x轴的距离是3;
(3)A(2x﹣4,x+2)在x轴上,则x的值是2;
(4)(﹣3,0)在y轴的负半轴上.
A.0 B.1 C.2 D.3
7.已知点P(a﹣5,a+1)在y轴上,则a的值为( )
A.1 B.﹣1 C.﹣5 D.5
8.在平面直角坐标系中,下列说法正确的是( )
A.点P(3,2)到x轴的距离是3
B.若ab=0,则点P(a,b)表示原点
C.若A(2,﹣2)、B(2,2),则直线AB∥x轴
D.第三象限内点的坐标,横纵坐标同号
9.已知点A的坐标为(﹣1,2),直线AB∥x轴,并且AB=4,则点B的坐标为( )
A.(﹣1,6) B.(﹣1,6)或(﹣1,﹣2)
C.(3,2) D.(3,2)或(﹣5,2)
10.如图所示,直角坐标系中四边形的面积是( )
A.15.5 B.20.5 C.26 D.31
二、填空题
11.某会场座位号将“7排4号”记作(7,4),那么“3排5号”记作 .
12.如图,在中国象棋的残局上建立平面直角坐标系,如果“相”的坐标是(4,1),那么“帅”的坐标为 .
13.已知点M(m+1,m+3)在x轴上,则m等于 .
14.如果点P在x轴下方,到x轴的距离是5,到y轴的距离是2,那么点P的坐标为 .
15.在平面直角坐标系中,点P(m,n)在第二象限,则点Q(﹣m+1,n)在第 象限.
16.在平面直角坐标系中,第二象限内有一点M,点M到x轴的距离为5,到y轴的距离为4,则点M的坐标是 .
17.如果点P(x,y)的坐标满足x+y=xy,那么称点P为“和谐点”,若某个“和谐点”到x轴的距离为3,则P点的坐标为 .
18.已知线段AB∥y轴,若点A的坐标为(5,n﹣1),B(n2+1,1),则n为 .
三、解答题
19.如图,在边长为1个单位长度的小正方形组成的网格中,小明家可用坐标(﹣1,2)表示,汽车站可用坐标(3,﹣1)表示.
(1)建立平面直角坐标系,画出x轴和y轴;
(2)某星期日早晨,小明同学从家出发,沿(0,1)→(﹣2,﹣1)→(﹣1,﹣2)→(0,﹣1)→(1,0)→(2,﹣1)→(2,2)的路线转了一圈,又回到家里,写出他路上经过的地方;
(3)连接他在上一问中经过的地点,你得到了什么图形?
20.如图是某市部分路段简图,若以超市为原点.
(1)请写出文化宫的坐标.
(2)李红家的坐标为(1,﹣1),请在图中标出李红家的位置.
(3)从超市到市场的一条线路可用(0,0)→(1,0)→(2,0)→(3,0)→(3,1)表示,类比上面的线路表示法,请你写出一条李红家到文化宫的路线图.
21.已知点P(2x﹣6,3x+1),求下列情形下点P的坐标.
(1)点P在y轴上;
(2)点P到x轴、y轴的距离相等,且点P在第二象限;
(3)点P在过点A(2,﹣4)且与y轴平行的直线上.
22.国庆假期期间,笑笑所在的学习小组组织了到方特梦幻王国的游园活动,笑笑和乐乐对着景区示意图(如图所示)讨论景点位置:(图中小正方形边长代表100m)
笑笑说:“西游传说坐标(300,300).”
乐乐说:“华夏五千年坐标(﹣100,﹣400).”
若他们二人所说的位置都正确
(1)在图中建立适当的平面直角坐标系xOy;
(2)用坐标描述其他地点的位置.
23.已知M(3|a|﹣9,4﹣2a)在y轴负半轴上,直线MN∥x轴,且线段MN长度为4.
(1)求点M的坐标;
(2)求(2﹣a)2020+1的值;
(3)求N点坐标.
24.点P是平面直角坐标系中的一点且不在坐标轴上,过点P向x轴、y轴作垂线段,若垂线段的长度的和为4,则点P叫做“垂距点”,例如:如图中的点P(1,3)是“垂距点”.
(1)在点A(﹣2,2),B(,),C(﹣1,5)中,“垂距点”是 ;
(2)若D(m,m)是“垂距点”,求m的值.
答案
一、选择题
A.B.B.D.D.B.D.D.D.A.
二、填空题
11.(3,5).
12.(0,﹣1).
13.﹣3..
14.(2,﹣5)或(﹣2,﹣5).
15.四.
16.(﹣4,5).
17.(,3)或(,﹣3).
18.﹣2.
三、解答题
19.(1)如图,建立平面直角坐标系;
(2)小明家﹣学校﹣奶奶家﹣宠物店﹣医院﹣公园﹣邮局﹣游乐场﹣消防站﹣小明家;
(3)连接他在上一问中经过的地点,得到“箭头”状的图形.
20.(1)以超市为原点,横坐标向右为正,向左为负,纵坐标向上为正,向下为负,可得文化宫的坐标为:(﹣1,2).
(2)李红家的坐标为(1,﹣1),在图中标出李红家的位置如下:
(3)一条李红家到文化宫的路线图如下:(1,﹣1)→(1,0)→(1,1)→(1,2)→(0,2)→(﹣1,2).
21.(1)∵点P(2x﹣6,3x+1),且点P在y轴上,
∴2x﹣6=0,
∴x=3,
∴3x+1=10,
∴点P的坐标为(0,10);
(2)∵点P(2x﹣6,3x+1),点P到x轴、y轴的距离相等,且点P在第二象限,
∴2x﹣6=﹣(3x+1),
∴2x﹣6+3x+1=0,
∴x=1,
∴2x﹣6=﹣4,3x+1=4,
∴点P的坐标为(﹣4,4);
(3)∵点P(2x﹣6,3x+1)在过点A(2,﹣4)且与y轴平行的直线上,
∴2x﹣6=2,
∴x=4,
∴3x+1=13,
∴点P的坐标为(2,13).
22.(1)如图所示:
(2)太空飞梭(0,0),秦岭历险(0,400),魔幻城堡(400,﹣200),南门(0,﹣500),丛林飞龙(﹣200,﹣100).
23.(1)∵M在y轴负半轴上,
∴3|a|﹣9=0,且4﹣2a<0,
∴a=±3,且a>2,
∴a=3.
∴4﹣2a=﹣2,
M(0,﹣2);
(2)∵a=3,
∴(2﹣a)2020+1
=(2﹣3)2020+1
=1+1
=2;
(3)∵直线MN∥x轴,M(0,﹣2),
∴设N(x,﹣2),
又∵线段MN长度为4,
∴MN=|x﹣0|=|x|=4,
∴x=±4,
∴N(4,﹣2)或(﹣4,﹣2).
24.(1)根据题意,对于点A而言,|﹣2|+|2|=4,
所以A是“垂距点”,
对于点B而言,||+||=3,
所以B不是“垂距点”,
对于点C而言,|﹣1|+|5|=6≠4,
所以C不是“垂距点”,
故答案为:A.
(2)由题意可知:,
①当m>0时,则4m=4,
解得m=1;
②当m<0时,则﹣4m=4,
解得m=﹣1;
∴m=±1.
