人教版数学八年级上册 13.3.1 等腰三角形 课时练习(含答案)
文档属性
| 名称 | 人教版数学八年级上册 13.3.1 等腰三角形 课时练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 108.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-10 00:00:00 | ||
图片预览



文档简介
2022-2023年人教版数学八年级上册13.3.1
《等腰三角形》课时练习
一 、选择题
1.等腰三角形的一个内角为70°,则另外两个内角的度数分别是( )
A.55°,55° B.70°,40°或70°,55°
C.70°,40° D.55°,55°或70°,40°
2.如图,在△ABC中,AB=AC,∠BAC=100°,AB的垂直平分线DE分别交AB、BC于点D、E,则∠BAE=( )
A.80° B.60° C.50° D.40°
3.如果等腰三角形的一个底角为α,那么( )
A.α不大于45° B.0°<α<90°
C.α不大于90° D.45°<α<90°
4.下列语句中,正确的是( )
A.等腰三角形底边上的中线就是底边上的垂直平分线
B.等腰三角形的对称轴是底边上的高
C.一条线段可看作是以它的垂直平分线为对称轴的轴对称图形
D.等腰三角形的对称轴就是顶角平分线
5.一个等腰三角形的两边长分别是3cm和7cm,则它的周长为( )
A.17cm B.15cm C.13cm D.13cm或17cm
6.如图,△ABC中,AB=AC,D是BC中点,下列结论中不正确的是( )
A.∠B=∠C B.AD⊥BC C.AD平分∠BAC D.AB=2BD
7.若(a﹣4)2+|b﹣6|=0,则以a、b为边长的等腰三角形的周长为( )
A.14 B.16 C.13 D.14或16
8.一个等腰三角形的一边长是7cm,另一边长为5cm,那么这个等腰三角形的周长是( )
A.12cm B.17cm C.19cm D.17cm或19cm
9.如图在等腰△ABC中,其中AB=AC,∠A=40°,P是△ABC内一点,且∠1=∠2,则∠BPC等于( )
A.110° B.120° C.130° D.140°
10.如图,在△ABC中,AB=AC,点D、E在BC上,连接AD、AE,如果只添加一个条件使∠DAB=∠EAC,则添加的条件不能为( )
A.BD=CE B.AD=AE C.DA=DE D.BE=CD
11.如图,是四张形状不同的纸片,用剪刀沿一条直线将它们分别剪开(只允许剪一次),不能得到两个等腰三角形纸片的是( )
12.如图,△ABC的面积为1cm2,AP垂直∠B的平分线BP于P,则△PBC面积为( )
A.0.4cm2 B.0.5cm2 C.0.6cm2 D.0.7cm2
二 、填空题
13.一个等腰三角形的周长为21,若有一边长为9,则等腰三角形的三边长为 .
14.等腰三角形一腰上的高与另一腰的夹角的度数为20°,则顶角的度数是 .
15.如图,在等腰△ABC中,AB=AC=BD,∠BAD=70°,∠DAC= .
16.等腰三角形中
①有一个角为100°,则另两个角的度数是 .
②有一个角为40°,则另两个角的度数是 .
17.如图,∠A=15°,AB=BC=CD=DE=EF,则∠MEF= .
18.如图,∠AOB=60°,OC平分∠AOB,如果射线OA上的点E满足△OCE是等腰三角形,那么∠OEC的度数为 .
三 、解答题
19.如图,已知AD=BC,AC=BD.
(1)求证:△ADB≌△BCA;
(2)OA与OB相等吗?若相等,请说明理由.
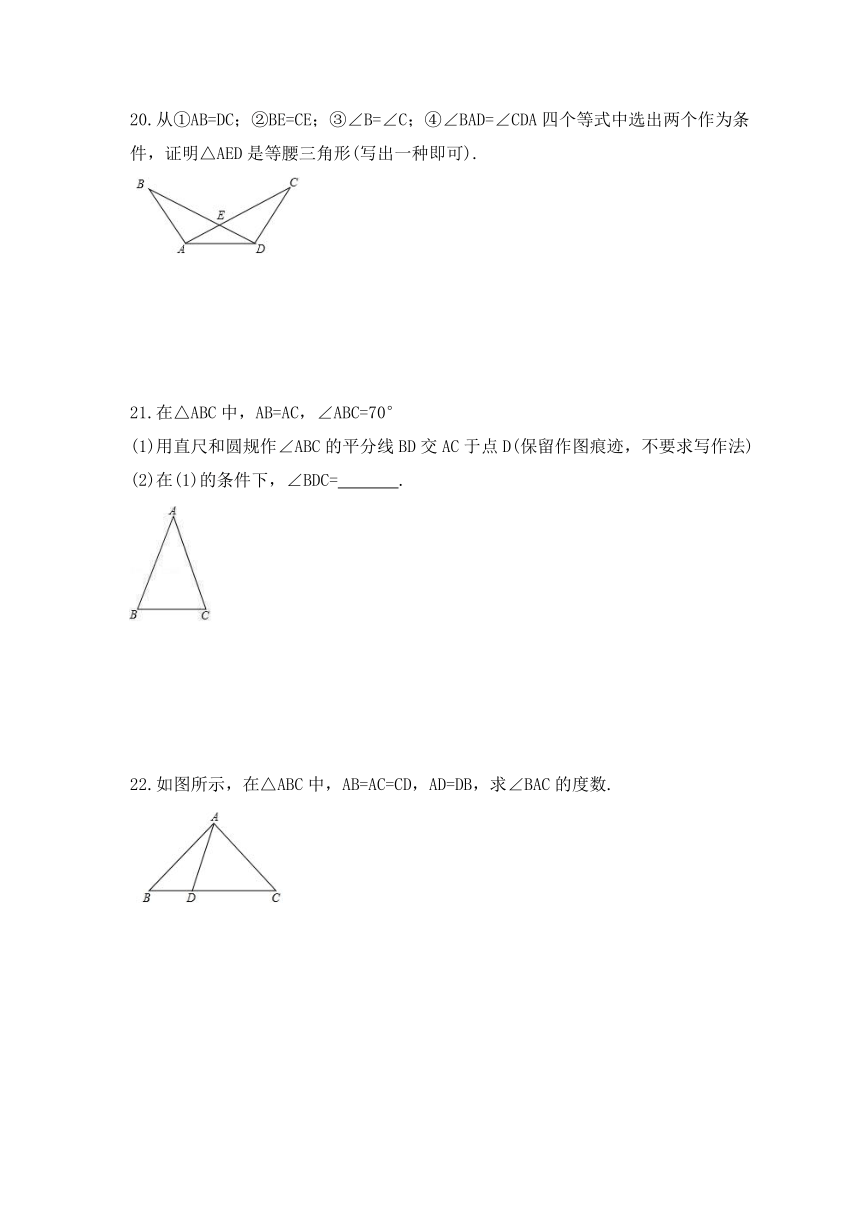
20.从①AB=DC;②BE=CE;③∠B=∠C;④∠BAD=∠CDA四个等式中选出两个作为条件,证明△AED是等腰三角形(写出一种即可).
21.在△ABC中,AB=AC,∠ABC=70°
(1)用直尺和圆规作∠ABC的平分线BD交AC于点D(保留作图痕迹,不要求写作法)
(2)在(1)的条件下,∠BDC= .
22.如图所示,在△ABC中,AB=AC=CD,AD=DB,求∠BAC的度数.
23.如图,在Rt△ABC中,∠ABC=90°,点O为AC中点,点E为线段BC上一点,∠EOF=90°,OF交AB于点F,求证:AF+CE>EF.
参考答案
1.D
2.D
3.B
4.C.
5.A.
6.D.
7.D.
8.D
9.A
10.C
11.B
12.B
13.答案为:6、6、9或9、9、3
14.答案为:110°或70°.
15.答案为:30°
16.答案为:40°,40°;100°,40°或70°,70°.
17.答案为:75°.
18.答案为:120°或75°或30°.
19.(1)证明:∵在△ADB和△BCA中,
,
∴△ADB≌△BCA(SSS);
(2)解:OA=OB,理由是:
∵△ADB≌△BCA,
∴∠ABD=∠BAC,
∴OA=OB.
20.解:选择的条件是:③∠B=∠C ④∠BAD=∠CDA(或①③,②③, ①④);
证明:在△BAD和△CDA中,
∵,
∴△BAD≌△CDA(AAS),
∴∠BDA=∠CAD
∴△AED是等腰三角形
21.解:(1)如图所示,BD即为所求;
(2)∵在△ABC中,AB=AC,∠ABC=70°,
∴∠A=180°﹣2∠ABC=180°﹣140°=40°,
∵BD是∠ABC的平分线,
∴∠ABD=∠ABC=×70°=35°,
∵∠BDC是△ABD的外角,
∴∠BDC=∠A+∠ABD=40°+35°=75°,
故答案为:75°.
22.解:∵AB=AC,DA=DB,
∴∠B=∠C=∠BAD,
∵CA=CD,
∴∠CDA=∠CAD,
又∠CDA=∠B+∠BAD=2∠B=2∠C,
∴∠CAD=2∠C,
在△ACD中,∠C+∠CDA+∠CAD=180°,
∴2∠C+2∠C+∠C=180°,
∴∠C=36°,
∴∠BAD=36°,∠CAD=2∠C=72°,
∴∠BAC=∠BAD+∠CAD=36°+72°=108°.
23.证明:延长FO到M,使FO=OM,连接CM,EM,
∵点O是AC的中点,
∴OA=OC,
在△AOF和△COM中,
,
∴△AOF≌△COM(SAS),
∴AF=CM,∠A=∠MCO,
∴AB∥CM,
∵∠B=90°,
∴∠MCE=90°,
∵∠EOF=90°,OF=OM,
∴EF=EM,
∵EF=EM,CM=AF,
∴AF+CE>EF.
《等腰三角形》课时练习
一 、选择题
1.等腰三角形的一个内角为70°,则另外两个内角的度数分别是( )
A.55°,55° B.70°,40°或70°,55°
C.70°,40° D.55°,55°或70°,40°
2.如图,在△ABC中,AB=AC,∠BAC=100°,AB的垂直平分线DE分别交AB、BC于点D、E,则∠BAE=( )
A.80° B.60° C.50° D.40°
3.如果等腰三角形的一个底角为α,那么( )
A.α不大于45° B.0°<α<90°
C.α不大于90° D.45°<α<90°
4.下列语句中,正确的是( )
A.等腰三角形底边上的中线就是底边上的垂直平分线
B.等腰三角形的对称轴是底边上的高
C.一条线段可看作是以它的垂直平分线为对称轴的轴对称图形
D.等腰三角形的对称轴就是顶角平分线
5.一个等腰三角形的两边长分别是3cm和7cm,则它的周长为( )
A.17cm B.15cm C.13cm D.13cm或17cm
6.如图,△ABC中,AB=AC,D是BC中点,下列结论中不正确的是( )
A.∠B=∠C B.AD⊥BC C.AD平分∠BAC D.AB=2BD
7.若(a﹣4)2+|b﹣6|=0,则以a、b为边长的等腰三角形的周长为( )
A.14 B.16 C.13 D.14或16
8.一个等腰三角形的一边长是7cm,另一边长为5cm,那么这个等腰三角形的周长是( )
A.12cm B.17cm C.19cm D.17cm或19cm
9.如图在等腰△ABC中,其中AB=AC,∠A=40°,P是△ABC内一点,且∠1=∠2,则∠BPC等于( )
A.110° B.120° C.130° D.140°
10.如图,在△ABC中,AB=AC,点D、E在BC上,连接AD、AE,如果只添加一个条件使∠DAB=∠EAC,则添加的条件不能为( )
A.BD=CE B.AD=AE C.DA=DE D.BE=CD
11.如图,是四张形状不同的纸片,用剪刀沿一条直线将它们分别剪开(只允许剪一次),不能得到两个等腰三角形纸片的是( )
12.如图,△ABC的面积为1cm2,AP垂直∠B的平分线BP于P,则△PBC面积为( )
A.0.4cm2 B.0.5cm2 C.0.6cm2 D.0.7cm2
二 、填空题
13.一个等腰三角形的周长为21,若有一边长为9,则等腰三角形的三边长为 .
14.等腰三角形一腰上的高与另一腰的夹角的度数为20°,则顶角的度数是 .
15.如图,在等腰△ABC中,AB=AC=BD,∠BAD=70°,∠DAC= .
16.等腰三角形中
①有一个角为100°,则另两个角的度数是 .
②有一个角为40°,则另两个角的度数是 .
17.如图,∠A=15°,AB=BC=CD=DE=EF,则∠MEF= .
18.如图,∠AOB=60°,OC平分∠AOB,如果射线OA上的点E满足△OCE是等腰三角形,那么∠OEC的度数为 .
三 、解答题
19.如图,已知AD=BC,AC=BD.
(1)求证:△ADB≌△BCA;
(2)OA与OB相等吗?若相等,请说明理由.
20.从①AB=DC;②BE=CE;③∠B=∠C;④∠BAD=∠CDA四个等式中选出两个作为条件,证明△AED是等腰三角形(写出一种即可).
21.在△ABC中,AB=AC,∠ABC=70°
(1)用直尺和圆规作∠ABC的平分线BD交AC于点D(保留作图痕迹,不要求写作法)
(2)在(1)的条件下,∠BDC= .
22.如图所示,在△ABC中,AB=AC=CD,AD=DB,求∠BAC的度数.
23.如图,在Rt△ABC中,∠ABC=90°,点O为AC中点,点E为线段BC上一点,∠EOF=90°,OF交AB于点F,求证:AF+CE>EF.
参考答案
1.D
2.D
3.B
4.C.
5.A.
6.D.
7.D.
8.D
9.A
10.C
11.B
12.B
13.答案为:6、6、9或9、9、3
14.答案为:110°或70°.
15.答案为:30°
16.答案为:40°,40°;100°,40°或70°,70°.
17.答案为:75°.
18.答案为:120°或75°或30°.
19.(1)证明:∵在△ADB和△BCA中,
,
∴△ADB≌△BCA(SSS);
(2)解:OA=OB,理由是:
∵△ADB≌△BCA,
∴∠ABD=∠BAC,
∴OA=OB.
20.解:选择的条件是:③∠B=∠C ④∠BAD=∠CDA(或①③,②③, ①④);
证明:在△BAD和△CDA中,
∵,
∴△BAD≌△CDA(AAS),
∴∠BDA=∠CAD
∴△AED是等腰三角形
21.解:(1)如图所示,BD即为所求;
(2)∵在△ABC中,AB=AC,∠ABC=70°,
∴∠A=180°﹣2∠ABC=180°﹣140°=40°,
∵BD是∠ABC的平分线,
∴∠ABD=∠ABC=×70°=35°,
∵∠BDC是△ABD的外角,
∴∠BDC=∠A+∠ABD=40°+35°=75°,
故答案为:75°.
22.解:∵AB=AC,DA=DB,
∴∠B=∠C=∠BAD,
∵CA=CD,
∴∠CDA=∠CAD,
又∠CDA=∠B+∠BAD=2∠B=2∠C,
∴∠CAD=2∠C,
在△ACD中,∠C+∠CDA+∠CAD=180°,
∴2∠C+2∠C+∠C=180°,
∴∠C=36°,
∴∠BAD=36°,∠CAD=2∠C=72°,
∴∠BAC=∠BAD+∠CAD=36°+72°=108°.
23.证明:延长FO到M,使FO=OM,连接CM,EM,
∵点O是AC的中点,
∴OA=OC,
在△AOF和△COM中,
,
∴△AOF≌△COM(SAS),
∴AF=CM,∠A=∠MCO,
∴AB∥CM,
∵∠B=90°,
∴∠MCE=90°,
∵∠EOF=90°,OF=OM,
∴EF=EM,
∵EF=EM,CM=AF,
∴AF+CE>EF.
