人教版八年级数学上册14.2乘法公式 课后练习(含解析)
文档属性
| 名称 | 人教版八年级数学上册14.2乘法公式 课后练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 130.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-10 17:42:49 | ||
图片预览




文档简介
14.2 乘法公式(课后练习)-人教版八年级上册
一.选择题
1.如图,有两个正方形A,B,现将B放置在A的内部得到图甲,将A、B并列放置,以正方形A与正方形B的边长之和为新的边长构造正方形得到图乙,若图甲和图乙中阴影部分的面积分别为1和8,则正方形A、B的面积之和为( )
A.8 B.9 C.10 D.12
2.已知(a+b)2=29,(a﹣b)2=13,则ab的值为( )
A.42 B.16 C.8 D.4
3.已知(2022﹣m)(2020﹣m)=2021,那么(2022﹣m)2+(2020﹣m)2的值为( )
A.4046 B.2023 C.4042 D.4043
4.下列四种说法中正确的有( )
①关于x、y的方程2x+6y=199存在整数解.
②若两个不等实数a、b满足2(a4+b4)=(a2+b2)2,则a、b互为相反数.
③若(a﹣c)2﹣4(a﹣b)(b﹣c)=0,则2b=a+c.
④若x2﹣yz=y2﹣xz=z2﹣xy,则x=y=z.
A.①④ B.②③ C.①②④ D.②③④
.如图,点C是线段BG上的一点,以BC,CG为边向两边作正方形,面积分别是S1和S2,两正方形的面积和S1+S2=40,已知BG=8,则图中阴影部分面积为( )
A.6 B.8 C.10 D.12
.下列计算正确的是( )
A.(a3)2=a6 B.a6÷a3=a2
C.3a+2b=5ab D.(a+b)2=a2+b2
.如果一个正整数能表示为两个正整数的平方差,那么这个正整数就称为“智慧数”,例如:7=7×1=(4+3)×(4﹣3)=42﹣32,7就是一个智慧数,8=4×2=(3+1)×(3﹣1)=32﹣12,8也是一个智慧数,则下列各数不是智慧数的是( )
A.2021 B.2022 C.2023 D.2024
.从前,一位农场主把一块边长为a米(a>4)的正方形土地租给租户张老汉,第二年,他对张老汉说:“我把这块地的一边增加4米,相邻的另一边减少4米,变成长方形土地继续租给你,租金不变,你也没有吃亏,你看如何?”如果这样,你觉得张老汉的租地面积会( )
A.没有变化 B.变大了 C.变小了 D.无法确定
.将四个长为a,宽为b(a>b)的长方形纸片,按如图的方式拼成一个边长为(a+b)的正方形,图中空白部分的面积为S1,阴影部分的面积为S2,若S1=2S2,则a,b满足( )
A.a=2b B.a=3b C.2a=3b D.2a=5b
.若9x2﹣(K﹣1)x+1是关于x的完全平方式,则常数K的值为( )
A.0 B.﹣5或7 C.7 D.9
二.填空题
.四张长为a、宽为b(a>b)的长方形纸片,按如图的方式拼成一个边长为(a+b)的正方形,图中空白部分的面积为S1,阴影部分的面积为S2.若S1=S2,则a:b= .
.如果多项式x2﹣2(m+1)xy+16y2是个完全平方式,则m= .
.如图,有两个正方形A,B,现将B放在A的内部得图甲,将A,B并列放置后构造新的正方形得图乙.若图甲和图乙中阴影部分的面积分别为3和15,则正方形A,B的面积之和为 .
.小淇将(2018x+2019)2展开后得到a1x2+b1x+c1;小尧将(2019x﹣2018)2展开后得到a2x2+b2x+c2,若两人计算过程无误,则c1﹣c2的值为 .
.4x2+Q+1是完全平方式,请你写一个满足条件的单项式Q是 .
三.解答题
.已知a+b=3,ab=﹣2,求下列各式的值:
(1)a2+b2;
(2)(a﹣2)(b﹣2);
(3)9a 27b÷3b﹣ab.
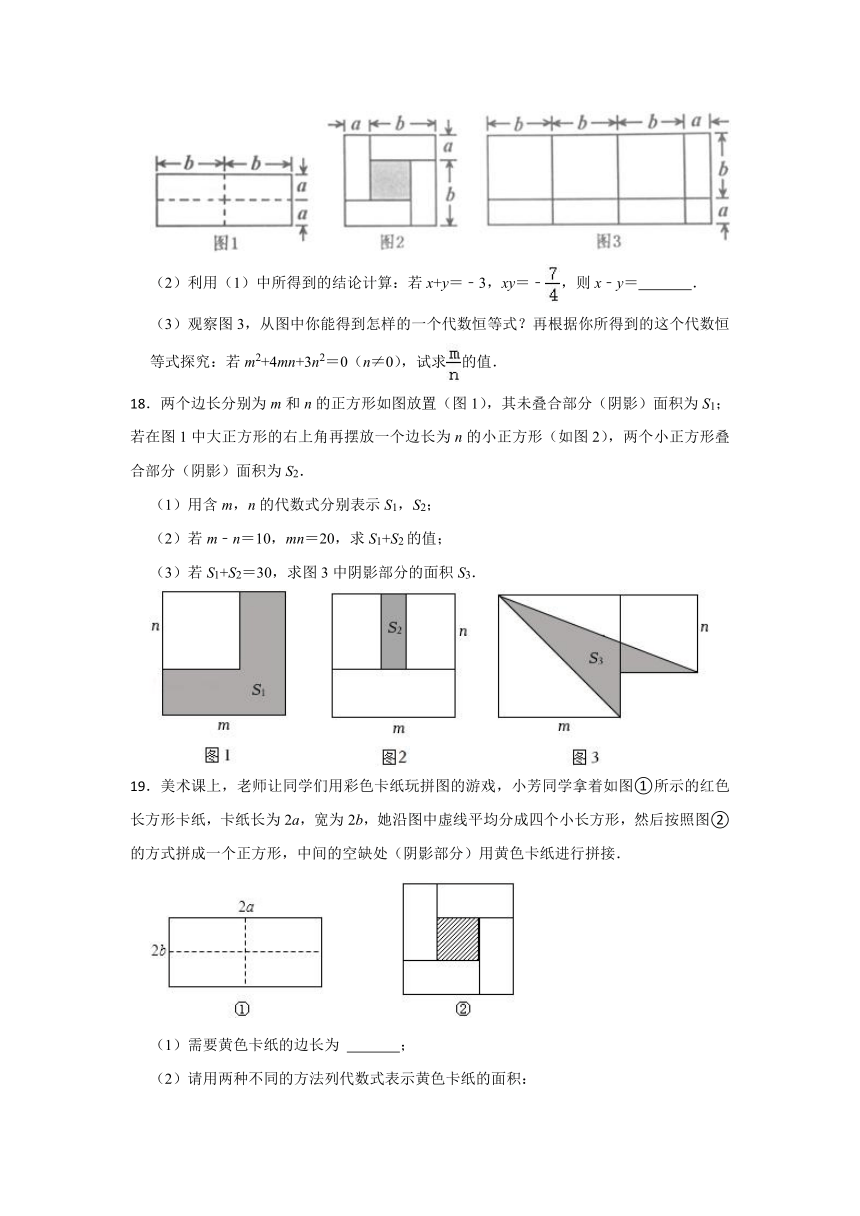
.图1是一个长为2b,宽为2a的长方形,沿虚线平均分成四块,然后按图2拼成一个正方形.解答下列问题.
(1)图2中阴影部分的面积可表示为 ;对于(b﹣a)2,(b+a)2,ab,这三者间的等量关系为 .
(2)利用(1)中所得到的结论计算:若x+y=﹣3,xy=﹣,则x﹣y= .
(3)观察图3,从图中你能得到怎样的一个代数恒等式?再根据你所得到的这个代数恒等式探究:若m2+4mn+3n2=0(n≠0),试求的值.
.两个边长分别为m和n的正方形如图放置(图1),其未叠合部分(阴影)面积为S1;若在图1中大正方形的右上角再摆放一个边长为n的小正方形(如图2),两个小正方形叠合部分(阴影)面积为S2.
(1)用含m,n的代数式分别表示S1,S2;
(2)若m﹣n=10,mn=20,求S1+S2的值;
(3)若S1+S2=30,求图3中阴影部分的面积S3.
.美术课上,老师让同学们用彩色卡纸玩拼图的游戏,小芳同学拿着如图①所示的红色长方形卡纸,卡纸长为2a,宽为2b,她沿图中虚线平均分成四个小长方形,然后按照图②的方式拼成一个正方形,中间的空缺处(阴影部分)用黄色卡纸进行拼接.
(1)需要黄色卡纸的边长为 ;
(2)请用两种不同的方法列代数式表示黄色卡纸的面积:
方法一 ;
方法二 ;
(3)观察图②直接写出(a+b)2,(a﹣b)2,ab这三个代数式之间的等量关系式 ;
(4)根据(3)中的等量关系解决下列问题:若a+b=6,ab=7,求(a﹣b)2的值.
.完全平方公式(a±b)2=a2±2ab+b2进行适当的变形后,可以解决很多的数学问题.
如:若x满足(9﹣x)(x﹣4)=4,求(9﹣x)2+(x﹣4)2的值.
解题思路:由(a+b)2=a2+2ab+b2得a2+b2=(a+b)2﹣2ab,
可设9﹣x=a,x﹣4=b,则(9﹣x)(x﹣4)=ab=4,a+b=(9﹣x)+(x﹣4)=5,
∴(9﹣x)2+(x﹣4)2=a2+b2=(a+b)2﹣2ab=52﹣2×4=17;
(1)请仿照上面的方法求解下面问题:
①若x满足(6﹣x)(x﹣2)=2,求(6﹣x)2+(x﹣2)2的值;
②若x满足(6+x)(2+x)=5,求(6+x)2+(2+x)2的值;
(2)应用上面的解题思路解决问题:如图,点C是线段AB上的一点,以AC,BC为边向两边作正方形,设AB=8,两正方形的面积和S1+S2=34,求图中阴影部分的面积.
参考答案与试题解析
一.选择题
1.【解答】解:设大小正方形边长分别为a、b,
S阴1=(a﹣b)2=1,即a2+b2﹣2ab=1,
S阴2=(a+b)2﹣a2﹣b2=8,得:ab=4.
∴a2+b2﹣2×4=1,
∴a2+b2=9.
故选:B.
2.【解答】解:∵(a+b)2=a2+2ab+b2,(a﹣b)2=a2﹣2ab+b2,
∴(a+b)2﹣(a﹣b)2=4ab,
∴29﹣13=4ab,
∴ab=4.
故选:D.
3.【解答】解:∵(a﹣b)2=a2﹣2ab+b2,
∴a2+b2=(a﹣b)2+2ab.
∴(2022﹣m)2+(2020﹣m)2
=[(2022﹣m)﹣(2020﹣m)]2+2×(2022﹣m)(2020﹣m)
=4+2×2021
=4046.
故选:A.
4.【解答】①因为x、y为整数时,2x+6y=2(x+3y)是偶数,而199是奇数,它们不可能相等;
故①错误.
②由2(a4+b4)=(a2+b2)2得:
2a4+2b4=a4+2a2b2+b4,
a4+b4﹣2a2b2=0,
(a2﹣b2)2=0,
∴a2﹣b2=0,
∴a2=b2,
∵a≠b,
∴a=﹣b,
即a、b互为相反数;
故②正确.
③若(a﹣c)2﹣4(a﹣b)(b﹣c)=0,则2b=a+c,
(a﹣c)2﹣4(a﹣b)(b﹣c)=0,
a2﹣2ac+c2﹣4ab+4ac+4b2﹣4bc=0,
a2+2ac+c2﹣4b(a+c)+4b2=0,
(a+c)2﹣4b(a+c)+4b2=0,
(a+c﹣2b)2=0,
∴a+c﹣2b=0,
∴2b=a+c;
故③正确.
④∵x2﹣yz=y2﹣xz=z2﹣xy,
∴x2﹣yz﹣y2+xz=0,
y2﹣xz﹣z2+xy=0,
∴(x+y+z)(x﹣y)=0,
(x+y+z)(y﹣z)=0.
∴x+y+z=0或x﹣y=0,y﹣z=0,
∴x=y=z或x+y+z=0,
故④错误.
综上所述,四种说法中正确的有②③,
故选:B.
.【解答】解:设BC=a,CG=b,则S1=a2,S2=b2,a+b=BG=8.
∴a2+b2=40.
∵(a+b)2=a2+b2+2ab=64,
∴2ab=64﹣40=24,
∴ab=12,
∴阴影部分的面积等于ab=×12=6.
故选:A.
.【解答】解:A.(a3)2=a6,所以A选项计算正确,故A选项符合题意;
B.a6÷a3=a3,所以B选项计算错误,故B选项不符合题意;
C.3a与2b不属于同类项,不能合并,故C选项不符合题意;
D.(a+b)2=a2+2ab+b2,所以D选项计算错误,故D选项不符合题意.
故选:A.
.【解答】解:∵2021
=2021×1
=(1011+1010)(1011﹣1010)
=10112﹣10102,
∴2021是智慧数,
∴选项A不符合题意;
∵2022不能写成两个正整数的平方差,
∴2022不是智慧数,
∴选项B符合题意;
∵2023
=2023×1
=(1012+1011)(1012﹣1011)
=10122﹣10112,
∴2023是智慧数,
∴选项C不符合题意;
∵2024
=1012×2
=(507+505)(507﹣505)
=5072﹣5052,
∴2024是智慧数,
∴选项D不符合题意;
故选:B.
.【解答】解:原来租的土地面积:a2(平方米).
现在租的土地面积:(a+4)(a﹣4)=a2﹣16(平方米).
∵a2>a2﹣16.
∴张老汉的租地面积会减少.
故选:C.
.【解答】解:∵S1=2×b(a+b)+2×ab+(a﹣b)2=a2+2b2,
S2=(a+b)2﹣(a2+2b2)
=2ab﹣b2,
又∵S1=2S2,
∴a2+2b2=2(2ab﹣b2),
整理,得(a﹣2b)2=0,
∴a﹣2b=0,
∴a=2b.
故选:A.
.【解答】解:9x2﹣(K﹣1)x+1=(3x)2﹣(K﹣1)x+12.
∵9x2﹣(K﹣1)x+1是关于x的完全平方式,
∴9x2﹣(K﹣1)x+1=(3x)2±2 3x 1+12=(3x)2±6x+12.
∴﹣(K﹣1)=±6.
当﹣(K﹣1)=6时,K=﹣5.
当﹣(K﹣1)=﹣6时,K=7.
综上:K=﹣5或7.
故选:B.
二.填空题
.【解答】解:由题意得:S2=4[ab+b2]==2ab+2b2.
S1=(a+b)2﹣S2=a2+2ab+b2﹣2ab﹣2b2=a2﹣b2.
∵S1=S2.
∴a2﹣b2=2ab+2b2.
∴a2﹣2ab﹣3b2=0.
∴(a﹣3b)(a+b)=0.
∵a>b>0.
∴a+b>0.
∴a﹣3b=0.
∴a=3b.
∴a:b=3:1.
故答案为:3:1.
.【解答】解:∵(x±4y)2=x2±8xy+16y2,
∴﹣2m﹣2=±8,
∴m=﹣5或3,
故答案为:﹣5或3.
.【解答】解:如图所示:
设正方形A、B的边长分别为x,y,依题意得:
,
化简得:
由①+②得:
x2+y2=18,
∴,
故答案为18.
.【解答】解:∵(2018x+2019)2展开后得到a1x2+b1x+c1;
∴c1=20192,
∵(2019x﹣2018)2展开后得到a2x2+b2x+c2,
∴c2=20182,
∴c1﹣c2=20192﹣20182=(2019+2018)(2019﹣2018)=4037,
故答案为:4037.
.【解答】解:∵4x2+1±4x=(2x±1)2;
4x2+1+4x4=(2x2+1)2;
4x2+1﹣1=(±2x)2;
4x2+1﹣4x2=(±1)2.
∴加上的单项式可以是±4x、4x4、﹣4x2、﹣1中任意一个.
故答案为±4x或4x4或﹣4x2或﹣1.
三.解答题
.【解答】解:(1)a2+b2
=(a+b)2﹣2ab
=32﹣2×(﹣2)
=9+4
=13;
(2)(a﹣2)(b﹣2)
=ab﹣2a﹣2b+4
=ab﹣2(a+b)+4
=﹣2﹣2×3+4
=﹣2﹣6+4
=﹣4;
(3)9a 27b÷3b﹣ab
=32a 33b÷3b﹣ab
=32a+3b﹣b+ab
=32a+2b+ab
=32(a+b)+ab
=32×3﹣2
=34
=81.
.【解答】解:(1)阴影部分是边长为b﹣a的正方形,因此面积为(b﹣a)2,
根据拼图以及面积之间的关系可得,(b﹣a)2,(b+a)2,ab,这三者间的等量关系为(b﹣a)2=(b+a)2﹣4ab,
故答案为:(b﹣a)2;(b﹣a)2=(b+a)2﹣4ab;
(2)由(1)可得,
(x﹣y)2=(x+y)2﹣4xy=9+7=16,
∴x﹣y=±4,
故答案为:±4;
(3)整个长方形是长为a+3b,宽为a+b,因此面积为(a+3b)(a+b),整个长方形的面积也可看作8个部分的面积和,即a2+4ab+3b2,
因此有(a+3b)(a+b)=a2+4ab+3b2;
∵m2+4mn+3n2=0(n≠0),即(m+n)(m+3n)=0,
∴m+n=0或m+3n=0,
∴=﹣1或=﹣3.
.【解答】解:(1)S1可以看作两个正方形的面积差,即S1=m2﹣n2,
S2是长为2n﹣m,高为n的长方形的面积,即S2=(2n﹣m) n=2n2﹣mn;
(2)∵m﹣n=10,mn=20,
∴S1+S2=m2﹣n2+2n2﹣mn
=m2+n2﹣mn
=(m﹣n)2+mn
=100+20
=120;
(3)∵S1+S2=m2+n2﹣mn=30,
∴S3=m2+n2﹣m2﹣n(m+n)
=m2﹣mn+n2
=(m2+n2﹣mn)
=×30
=15.
.【解答】解:(1)根据图形可观察出:边长为a﹣b;
故答案为:a﹣b;
(2)①小正方的边长为a﹣b,面积可表示为:(a﹣b)2,
大正方形的面积为:(a+b)2,
四个矩形的面积和为4ab,
所以小正方形面积可表示为:(a+b)2﹣4ab;
故答案为:(a﹣b)2,(a+b)2﹣4ab;
(3)由题意得:(a﹣b)2=(a+b)2﹣4ab;
故答案为:(a﹣b)2=(a+b)2﹣4ab;
(4)由(3)很快可求出(a﹣b)2=(a+b)2﹣4ab=62﹣4×7=8.
.【解答】解:(1)①设a=6﹣x,b=x﹣2,则(6﹣x)+(x﹣2)=a+b=4,
∴(6﹣x)2+(x﹣2)2=a2+b2=(a+b)2﹣2ab=16﹣4=12;
②设a=6+x,b=2+x,则(6+x)﹣(2+x)=a﹣b=4,
∴(6+x)2+(2+x)2=a2+b2=(a﹣b)2+2ab=16+10=26;
(2)设AC=m,CF=n,
∵AB=8,
∴m+n=8,
又∵S1+S2=34,
∴m2+n2=34,
由完全平方公式可得,(m+n)2=m2+2mn+n2,
∴82=34+2mn,
∴mn=15,
∴S阴影部分=0.5mn=0.5×25=7.5,
所以阴影部分的面积为7.5.
一.选择题
1.如图,有两个正方形A,B,现将B放置在A的内部得到图甲,将A、B并列放置,以正方形A与正方形B的边长之和为新的边长构造正方形得到图乙,若图甲和图乙中阴影部分的面积分别为1和8,则正方形A、B的面积之和为( )
A.8 B.9 C.10 D.12
2.已知(a+b)2=29,(a﹣b)2=13,则ab的值为( )
A.42 B.16 C.8 D.4
3.已知(2022﹣m)(2020﹣m)=2021,那么(2022﹣m)2+(2020﹣m)2的值为( )
A.4046 B.2023 C.4042 D.4043
4.下列四种说法中正确的有( )
①关于x、y的方程2x+6y=199存在整数解.
②若两个不等实数a、b满足2(a4+b4)=(a2+b2)2,则a、b互为相反数.
③若(a﹣c)2﹣4(a﹣b)(b﹣c)=0,则2b=a+c.
④若x2﹣yz=y2﹣xz=z2﹣xy,则x=y=z.
A.①④ B.②③ C.①②④ D.②③④
.如图,点C是线段BG上的一点,以BC,CG为边向两边作正方形,面积分别是S1和S2,两正方形的面积和S1+S2=40,已知BG=8,则图中阴影部分面积为( )
A.6 B.8 C.10 D.12
.下列计算正确的是( )
A.(a3)2=a6 B.a6÷a3=a2
C.3a+2b=5ab D.(a+b)2=a2+b2
.如果一个正整数能表示为两个正整数的平方差,那么这个正整数就称为“智慧数”,例如:7=7×1=(4+3)×(4﹣3)=42﹣32,7就是一个智慧数,8=4×2=(3+1)×(3﹣1)=32﹣12,8也是一个智慧数,则下列各数不是智慧数的是( )
A.2021 B.2022 C.2023 D.2024
.从前,一位农场主把一块边长为a米(a>4)的正方形土地租给租户张老汉,第二年,他对张老汉说:“我把这块地的一边增加4米,相邻的另一边减少4米,变成长方形土地继续租给你,租金不变,你也没有吃亏,你看如何?”如果这样,你觉得张老汉的租地面积会( )
A.没有变化 B.变大了 C.变小了 D.无法确定
.将四个长为a,宽为b(a>b)的长方形纸片,按如图的方式拼成一个边长为(a+b)的正方形,图中空白部分的面积为S1,阴影部分的面积为S2,若S1=2S2,则a,b满足( )
A.a=2b B.a=3b C.2a=3b D.2a=5b
.若9x2﹣(K﹣1)x+1是关于x的完全平方式,则常数K的值为( )
A.0 B.﹣5或7 C.7 D.9
二.填空题
.四张长为a、宽为b(a>b)的长方形纸片,按如图的方式拼成一个边长为(a+b)的正方形,图中空白部分的面积为S1,阴影部分的面积为S2.若S1=S2,则a:b= .
.如果多项式x2﹣2(m+1)xy+16y2是个完全平方式,则m= .
.如图,有两个正方形A,B,现将B放在A的内部得图甲,将A,B并列放置后构造新的正方形得图乙.若图甲和图乙中阴影部分的面积分别为3和15,则正方形A,B的面积之和为 .
.小淇将(2018x+2019)2展开后得到a1x2+b1x+c1;小尧将(2019x﹣2018)2展开后得到a2x2+b2x+c2,若两人计算过程无误,则c1﹣c2的值为 .
.4x2+Q+1是完全平方式,请你写一个满足条件的单项式Q是 .
三.解答题
.已知a+b=3,ab=﹣2,求下列各式的值:
(1)a2+b2;
(2)(a﹣2)(b﹣2);
(3)9a 27b÷3b﹣ab.
.图1是一个长为2b,宽为2a的长方形,沿虚线平均分成四块,然后按图2拼成一个正方形.解答下列问题.
(1)图2中阴影部分的面积可表示为 ;对于(b﹣a)2,(b+a)2,ab,这三者间的等量关系为 .
(2)利用(1)中所得到的结论计算:若x+y=﹣3,xy=﹣,则x﹣y= .
(3)观察图3,从图中你能得到怎样的一个代数恒等式?再根据你所得到的这个代数恒等式探究:若m2+4mn+3n2=0(n≠0),试求的值.
.两个边长分别为m和n的正方形如图放置(图1),其未叠合部分(阴影)面积为S1;若在图1中大正方形的右上角再摆放一个边长为n的小正方形(如图2),两个小正方形叠合部分(阴影)面积为S2.
(1)用含m,n的代数式分别表示S1,S2;
(2)若m﹣n=10,mn=20,求S1+S2的值;
(3)若S1+S2=30,求图3中阴影部分的面积S3.
.美术课上,老师让同学们用彩色卡纸玩拼图的游戏,小芳同学拿着如图①所示的红色长方形卡纸,卡纸长为2a,宽为2b,她沿图中虚线平均分成四个小长方形,然后按照图②的方式拼成一个正方形,中间的空缺处(阴影部分)用黄色卡纸进行拼接.
(1)需要黄色卡纸的边长为 ;
(2)请用两种不同的方法列代数式表示黄色卡纸的面积:
方法一 ;
方法二 ;
(3)观察图②直接写出(a+b)2,(a﹣b)2,ab这三个代数式之间的等量关系式 ;
(4)根据(3)中的等量关系解决下列问题:若a+b=6,ab=7,求(a﹣b)2的值.
.完全平方公式(a±b)2=a2±2ab+b2进行适当的变形后,可以解决很多的数学问题.
如:若x满足(9﹣x)(x﹣4)=4,求(9﹣x)2+(x﹣4)2的值.
解题思路:由(a+b)2=a2+2ab+b2得a2+b2=(a+b)2﹣2ab,
可设9﹣x=a,x﹣4=b,则(9﹣x)(x﹣4)=ab=4,a+b=(9﹣x)+(x﹣4)=5,
∴(9﹣x)2+(x﹣4)2=a2+b2=(a+b)2﹣2ab=52﹣2×4=17;
(1)请仿照上面的方法求解下面问题:
①若x满足(6﹣x)(x﹣2)=2,求(6﹣x)2+(x﹣2)2的值;
②若x满足(6+x)(2+x)=5,求(6+x)2+(2+x)2的值;
(2)应用上面的解题思路解决问题:如图,点C是线段AB上的一点,以AC,BC为边向两边作正方形,设AB=8,两正方形的面积和S1+S2=34,求图中阴影部分的面积.
参考答案与试题解析
一.选择题
1.【解答】解:设大小正方形边长分别为a、b,
S阴1=(a﹣b)2=1,即a2+b2﹣2ab=1,
S阴2=(a+b)2﹣a2﹣b2=8,得:ab=4.
∴a2+b2﹣2×4=1,
∴a2+b2=9.
故选:B.
2.【解答】解:∵(a+b)2=a2+2ab+b2,(a﹣b)2=a2﹣2ab+b2,
∴(a+b)2﹣(a﹣b)2=4ab,
∴29﹣13=4ab,
∴ab=4.
故选:D.
3.【解答】解:∵(a﹣b)2=a2﹣2ab+b2,
∴a2+b2=(a﹣b)2+2ab.
∴(2022﹣m)2+(2020﹣m)2
=[(2022﹣m)﹣(2020﹣m)]2+2×(2022﹣m)(2020﹣m)
=4+2×2021
=4046.
故选:A.
4.【解答】①因为x、y为整数时,2x+6y=2(x+3y)是偶数,而199是奇数,它们不可能相等;
故①错误.
②由2(a4+b4)=(a2+b2)2得:
2a4+2b4=a4+2a2b2+b4,
a4+b4﹣2a2b2=0,
(a2﹣b2)2=0,
∴a2﹣b2=0,
∴a2=b2,
∵a≠b,
∴a=﹣b,
即a、b互为相反数;
故②正确.
③若(a﹣c)2﹣4(a﹣b)(b﹣c)=0,则2b=a+c,
(a﹣c)2﹣4(a﹣b)(b﹣c)=0,
a2﹣2ac+c2﹣4ab+4ac+4b2﹣4bc=0,
a2+2ac+c2﹣4b(a+c)+4b2=0,
(a+c)2﹣4b(a+c)+4b2=0,
(a+c﹣2b)2=0,
∴a+c﹣2b=0,
∴2b=a+c;
故③正确.
④∵x2﹣yz=y2﹣xz=z2﹣xy,
∴x2﹣yz﹣y2+xz=0,
y2﹣xz﹣z2+xy=0,
∴(x+y+z)(x﹣y)=0,
(x+y+z)(y﹣z)=0.
∴x+y+z=0或x﹣y=0,y﹣z=0,
∴x=y=z或x+y+z=0,
故④错误.
综上所述,四种说法中正确的有②③,
故选:B.
.【解答】解:设BC=a,CG=b,则S1=a2,S2=b2,a+b=BG=8.
∴a2+b2=40.
∵(a+b)2=a2+b2+2ab=64,
∴2ab=64﹣40=24,
∴ab=12,
∴阴影部分的面积等于ab=×12=6.
故选:A.
.【解答】解:A.(a3)2=a6,所以A选项计算正确,故A选项符合题意;
B.a6÷a3=a3,所以B选项计算错误,故B选项不符合题意;
C.3a与2b不属于同类项,不能合并,故C选项不符合题意;
D.(a+b)2=a2+2ab+b2,所以D选项计算错误,故D选项不符合题意.
故选:A.
.【解答】解:∵2021
=2021×1
=(1011+1010)(1011﹣1010)
=10112﹣10102,
∴2021是智慧数,
∴选项A不符合题意;
∵2022不能写成两个正整数的平方差,
∴2022不是智慧数,
∴选项B符合题意;
∵2023
=2023×1
=(1012+1011)(1012﹣1011)
=10122﹣10112,
∴2023是智慧数,
∴选项C不符合题意;
∵2024
=1012×2
=(507+505)(507﹣505)
=5072﹣5052,
∴2024是智慧数,
∴选项D不符合题意;
故选:B.
.【解答】解:原来租的土地面积:a2(平方米).
现在租的土地面积:(a+4)(a﹣4)=a2﹣16(平方米).
∵a2>a2﹣16.
∴张老汉的租地面积会减少.
故选:C.
.【解答】解:∵S1=2×b(a+b)+2×ab+(a﹣b)2=a2+2b2,
S2=(a+b)2﹣(a2+2b2)
=2ab﹣b2,
又∵S1=2S2,
∴a2+2b2=2(2ab﹣b2),
整理,得(a﹣2b)2=0,
∴a﹣2b=0,
∴a=2b.
故选:A.
.【解答】解:9x2﹣(K﹣1)x+1=(3x)2﹣(K﹣1)x+12.
∵9x2﹣(K﹣1)x+1是关于x的完全平方式,
∴9x2﹣(K﹣1)x+1=(3x)2±2 3x 1+12=(3x)2±6x+12.
∴﹣(K﹣1)=±6.
当﹣(K﹣1)=6时,K=﹣5.
当﹣(K﹣1)=﹣6时,K=7.
综上:K=﹣5或7.
故选:B.
二.填空题
.【解答】解:由题意得:S2=4[ab+b2]==2ab+2b2.
S1=(a+b)2﹣S2=a2+2ab+b2﹣2ab﹣2b2=a2﹣b2.
∵S1=S2.
∴a2﹣b2=2ab+2b2.
∴a2﹣2ab﹣3b2=0.
∴(a﹣3b)(a+b)=0.
∵a>b>0.
∴a+b>0.
∴a﹣3b=0.
∴a=3b.
∴a:b=3:1.
故答案为:3:1.
.【解答】解:∵(x±4y)2=x2±8xy+16y2,
∴﹣2m﹣2=±8,
∴m=﹣5或3,
故答案为:﹣5或3.
.【解答】解:如图所示:
设正方形A、B的边长分别为x,y,依题意得:
,
化简得:
由①+②得:
x2+y2=18,
∴,
故答案为18.
.【解答】解:∵(2018x+2019)2展开后得到a1x2+b1x+c1;
∴c1=20192,
∵(2019x﹣2018)2展开后得到a2x2+b2x+c2,
∴c2=20182,
∴c1﹣c2=20192﹣20182=(2019+2018)(2019﹣2018)=4037,
故答案为:4037.
.【解答】解:∵4x2+1±4x=(2x±1)2;
4x2+1+4x4=(2x2+1)2;
4x2+1﹣1=(±2x)2;
4x2+1﹣4x2=(±1)2.
∴加上的单项式可以是±4x、4x4、﹣4x2、﹣1中任意一个.
故答案为±4x或4x4或﹣4x2或﹣1.
三.解答题
.【解答】解:(1)a2+b2
=(a+b)2﹣2ab
=32﹣2×(﹣2)
=9+4
=13;
(2)(a﹣2)(b﹣2)
=ab﹣2a﹣2b+4
=ab﹣2(a+b)+4
=﹣2﹣2×3+4
=﹣2﹣6+4
=﹣4;
(3)9a 27b÷3b﹣ab
=32a 33b÷3b﹣ab
=32a+3b﹣b+ab
=32a+2b+ab
=32(a+b)+ab
=32×3﹣2
=34
=81.
.【解答】解:(1)阴影部分是边长为b﹣a的正方形,因此面积为(b﹣a)2,
根据拼图以及面积之间的关系可得,(b﹣a)2,(b+a)2,ab,这三者间的等量关系为(b﹣a)2=(b+a)2﹣4ab,
故答案为:(b﹣a)2;(b﹣a)2=(b+a)2﹣4ab;
(2)由(1)可得,
(x﹣y)2=(x+y)2﹣4xy=9+7=16,
∴x﹣y=±4,
故答案为:±4;
(3)整个长方形是长为a+3b,宽为a+b,因此面积为(a+3b)(a+b),整个长方形的面积也可看作8个部分的面积和,即a2+4ab+3b2,
因此有(a+3b)(a+b)=a2+4ab+3b2;
∵m2+4mn+3n2=0(n≠0),即(m+n)(m+3n)=0,
∴m+n=0或m+3n=0,
∴=﹣1或=﹣3.
.【解答】解:(1)S1可以看作两个正方形的面积差,即S1=m2﹣n2,
S2是长为2n﹣m,高为n的长方形的面积,即S2=(2n﹣m) n=2n2﹣mn;
(2)∵m﹣n=10,mn=20,
∴S1+S2=m2﹣n2+2n2﹣mn
=m2+n2﹣mn
=(m﹣n)2+mn
=100+20
=120;
(3)∵S1+S2=m2+n2﹣mn=30,
∴S3=m2+n2﹣m2﹣n(m+n)
=m2﹣mn+n2
=(m2+n2﹣mn)
=×30
=15.
.【解答】解:(1)根据图形可观察出:边长为a﹣b;
故答案为:a﹣b;
(2)①小正方的边长为a﹣b,面积可表示为:(a﹣b)2,
大正方形的面积为:(a+b)2,
四个矩形的面积和为4ab,
所以小正方形面积可表示为:(a+b)2﹣4ab;
故答案为:(a﹣b)2,(a+b)2﹣4ab;
(3)由题意得:(a﹣b)2=(a+b)2﹣4ab;
故答案为:(a﹣b)2=(a+b)2﹣4ab;
(4)由(3)很快可求出(a﹣b)2=(a+b)2﹣4ab=62﹣4×7=8.
.【解答】解:(1)①设a=6﹣x,b=x﹣2,则(6﹣x)+(x﹣2)=a+b=4,
∴(6﹣x)2+(x﹣2)2=a2+b2=(a+b)2﹣2ab=16﹣4=12;
②设a=6+x,b=2+x,则(6+x)﹣(2+x)=a﹣b=4,
∴(6+x)2+(2+x)2=a2+b2=(a﹣b)2+2ab=16+10=26;
(2)设AC=m,CF=n,
∵AB=8,
∴m+n=8,
又∵S1+S2=34,
∴m2+n2=34,
由完全平方公式可得,(m+n)2=m2+2mn+n2,
∴82=34+2mn,
∴mn=15,
∴S阴影部分=0.5mn=0.5×25=7.5,
所以阴影部分的面积为7.5.
