华东师大版九年级数学上册23.3.2.3用边的关系判定三角形相似 同步精练(含答案)
文档属性
| 名称 | 华东师大版九年级数学上册23.3.2.3用边的关系判定三角形相似 同步精练(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 225.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-10 18:09:44 | ||
图片预览


文档简介
用边的关系判定三角形相似
同步精练
一、选择题(共10小题,每小题4分,共40分)
1. 如图,D是△ABC的边AB上一点,要使△ACD∽△ABC,则它们必须具备的条件是( )
A.= B.=
C.CD2=AD·DB D.AC2=AD·AB
2. 有甲、乙两个三角形木框,甲三角形木框的三边长分别为1,,,乙三角形木框的三边长分别为5,,,则甲、乙两个三角形( )
A.一定相似 B.一定不相似
C.不一定相似 D.无法判断
3. 如图,小正方形的边长均为1,则下列图中的三角形(阴影部分)与△A1B1C1相似的是( )
4. 已知△ABC的三边长分别为6 cm,7.5 cm,9 cm,△DEF的一边长为4 cm,当△DEF的另两边长是下列哪一组时,这两个三角形相似( )
A.2 cm,3 cm B.4 cm,5 cm
C.5 cm,6 cm D.6 cm,7 cm
5. 已知△ABC的三边长分别为4 cm,5 cm,6 cm,△DEF的一边长为2 cm,若两个三角形相似,则△DEF的另两边长不可能是( )
A.2.5 cm,3 cm B.1.6 cm,2.4 cm
C. cm, cm D.1.6 cm,2.5 cm
6. 一个三角形木架三边长分别是75 cm,100 cm,120 cm,现要再做一个与其相似的三角形木架,而只有长为60 cm和120 cm的两根木条.要求以其中一根为一边,从另一根截下两段作为另两边(允许有余料),则不同的截法有( )
A.一种 B.两种 C.三种 D.四种
7. 要做甲、乙两个形状相同的三角形框架,已知三角形框架甲的三边长分别为50 cm,60 cm,80 cm,三角形框架乙的一边长为20 cm,那么符合条件的三角形框架乙共有( )
A.1种 B.2种 C.3种 D.4种
8. 如图,在4×4的正方形网格中,是相似三角形的是( )
A.①和② B.②和③
C.①和③ D.②和④
9. 如图,在4×4的正方形网格中,每个小正方形的边长都为1,E为BD与正方形网格线的交点,下列结论正确的是( )
A.CE≠BD B.△ABC≌△CBD
C.AC=CD D.∠ABC=∠CBD
10. 如图,在△ABC中,P为AB上的一点,在下列四个条件中:①∠ACP=∠B;②∠APC=∠ACB;③AC2=AP·AB;④AB·CP=AP·CB,能满足△APC和△ACB相似的条件是( )
A.①②④ B.①③④
C.②③④ D.①②③
二.填空题(共6小题,每小题4分,共24分)
11. △ABC的三边长分别为6,8,12,△A′B′C′的三边长分别为2,3,2.5,△A″B″C″的三边长分别为6,3,4,则△ABC与___________________相似.
12. 如图,若==,则∠BAD= .
13. △ABC的三边长分别为1,,2,△A′B′C′的较短的边长为,△A′B′C′的另外两边为___________时,△ABC∽△A′B′C′.
14. 若△ABC各边分别为AB=10 cm,BC=8 cm,AC=6 cm,△DEF的两边为DE=5 cm,EF=4 cm,则当DF=________cm时,△ABC∽△DEF.
15. 在平面直角坐标系中,A(2,0),B(1,2),A1(0,-4),B1(4,-2),则△AOB与△A1OB1的关系是________(填“相似”或“不相似”).
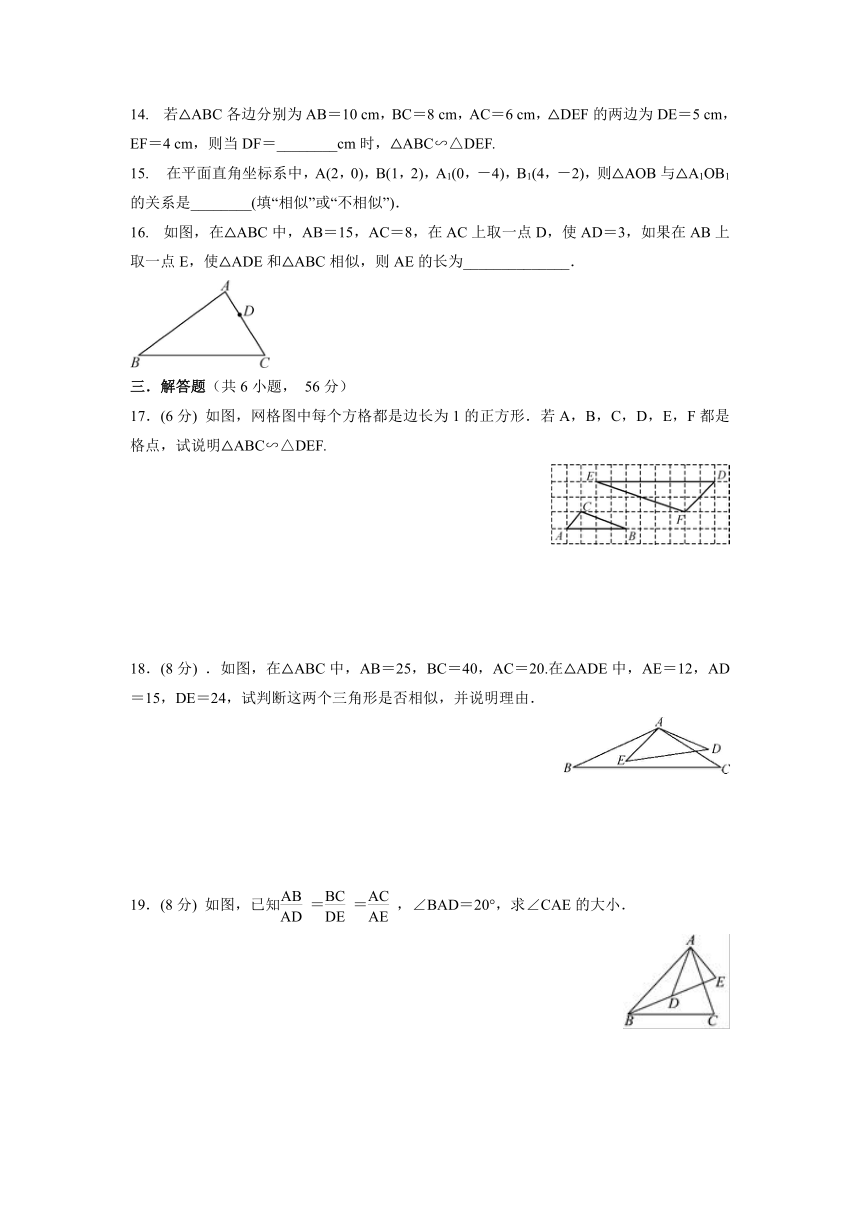
16. 如图,在△ABC中,AB=15,AC=8,在AC上取一点D,使AD=3,如果在AB上取一点E,使△ADE和△ABC相似,则AE的长为______________.
三.解答题(共6小题, 56分)
17.(6分) 如图,网格图中每个方格都是边长为1的正方形.若A,B,C,D,E,F都是格点,试说明△ABC∽△DEF.
18.(8分) .如图,在△ABC中,AB=25,BC=40,AC=20.在△ADE中,AE=12,AD=15,DE=24,试判断这两个三角形是否相似,并说明理由.
19.(8分) 如图,已知==,∠BAD=20°,求∠CAE的大小.
20.(10分) 根据下列条件,判断△ABC与△A′B′C′是否相似,并说明理由.
(1)AB=12,BC=15,AC=24,A′B′=25,B′C′=40,C′A′=20;
(2)AB=3,BC=4,AC=5,A′B′=12,B′C′=16,C′A′=20.
21.(12分) 如图,四边形ABCD,CDEF,EFGH都是边长相等的正方形.
(1)△ACF与△GCA相似吗?说说你的理由.
(2)求∠1+∠2的度数.
22.(12分) 如图,点B,D,E在一条直线上,BE与AC相交于点F,==.
(1)求证:∠BAD=∠CAE;
(2)若∠BAD=21°,求∠EBC的度数;
(3)连结EC,求证:△ABD∽△ACE.
参考答案
1-5DABCD 6-10BCCDD
11.△A″B″C″
12.∠CAE
13.,2
14.3
15.相似
16.或
17. 解:∵AC=,BC==,AB=4,DF==2,EF==2,ED=8,∴===,∴△ABC∽△DEF.
18. 解:相似.理由:∵==,==,==,∴==,∴△ABC∽△ADE
19.解:∵==,∴△ABC∽△ADE,∴∠BAC=∠DAE,又∠DAC是公共角,∴∠CAE=∠BAD=20°
20. 解:(1)△ABC与△A′B′C′相似.理由如下:∵==,==,==,∴==,∴△ABC ∽△C′A′B′.
(2)△ABC与△A′B′C′相似.理由如下:∵==,==,==,∴==,∴△ABC ∽△A′B′C′.
21. 解:(1)△ACF与△GCA相似.理由:可设正方形ABCD,CDEF,EFGH的边长为a,则△ACF的三边长分别为AC=a,CF=a,AF=a,△GCA的三边长分别为AC=a,CG=2a,AG=a.∴==,==,==.∴==.∴△ACF与△GCA相似.
(2)∵△ACF∽△GCA,∴∠1=∠CAF.∴∠1+∠2=∠CAF+∠2=∠ACB=45°.
22. 解:(1)∵==,∴△ABC ∽△ADE,∴∠BAC=∠DAE,∴∠BAC-∠DAF=∠DAE-∠DAF,∴∠BAD=∠CAE.
(2)∵△ABC ∽△ADE,∴∠ABC=∠ADE.∵∠ABC=∠ABE+∠EBC,∠ADE=∠ABE+∠BAD,∴∠EBC=∠BAD=21°.
(3)由(1)得∠BAD=∠CAE. 又∵=,∴△ABD ∽△ACE.
同步精练
一、选择题(共10小题,每小题4分,共40分)
1. 如图,D是△ABC的边AB上一点,要使△ACD∽△ABC,则它们必须具备的条件是( )
A.= B.=
C.CD2=AD·DB D.AC2=AD·AB
2. 有甲、乙两个三角形木框,甲三角形木框的三边长分别为1,,,乙三角形木框的三边长分别为5,,,则甲、乙两个三角形( )
A.一定相似 B.一定不相似
C.不一定相似 D.无法判断
3. 如图,小正方形的边长均为1,则下列图中的三角形(阴影部分)与△A1B1C1相似的是( )
4. 已知△ABC的三边长分别为6 cm,7.5 cm,9 cm,△DEF的一边长为4 cm,当△DEF的另两边长是下列哪一组时,这两个三角形相似( )
A.2 cm,3 cm B.4 cm,5 cm
C.5 cm,6 cm D.6 cm,7 cm
5. 已知△ABC的三边长分别为4 cm,5 cm,6 cm,△DEF的一边长为2 cm,若两个三角形相似,则△DEF的另两边长不可能是( )
A.2.5 cm,3 cm B.1.6 cm,2.4 cm
C. cm, cm D.1.6 cm,2.5 cm
6. 一个三角形木架三边长分别是75 cm,100 cm,120 cm,现要再做一个与其相似的三角形木架,而只有长为60 cm和120 cm的两根木条.要求以其中一根为一边,从另一根截下两段作为另两边(允许有余料),则不同的截法有( )
A.一种 B.两种 C.三种 D.四种
7. 要做甲、乙两个形状相同的三角形框架,已知三角形框架甲的三边长分别为50 cm,60 cm,80 cm,三角形框架乙的一边长为20 cm,那么符合条件的三角形框架乙共有( )
A.1种 B.2种 C.3种 D.4种
8. 如图,在4×4的正方形网格中,是相似三角形的是( )
A.①和② B.②和③
C.①和③ D.②和④
9. 如图,在4×4的正方形网格中,每个小正方形的边长都为1,E为BD与正方形网格线的交点,下列结论正确的是( )
A.CE≠BD B.△ABC≌△CBD
C.AC=CD D.∠ABC=∠CBD
10. 如图,在△ABC中,P为AB上的一点,在下列四个条件中:①∠ACP=∠B;②∠APC=∠ACB;③AC2=AP·AB;④AB·CP=AP·CB,能满足△APC和△ACB相似的条件是( )
A.①②④ B.①③④
C.②③④ D.①②③
二.填空题(共6小题,每小题4分,共24分)
11. △ABC的三边长分别为6,8,12,△A′B′C′的三边长分别为2,3,2.5,△A″B″C″的三边长分别为6,3,4,则△ABC与___________________相似.
12. 如图,若==,则∠BAD= .
13. △ABC的三边长分别为1,,2,△A′B′C′的较短的边长为,△A′B′C′的另外两边为___________时,△ABC∽△A′B′C′.
14. 若△ABC各边分别为AB=10 cm,BC=8 cm,AC=6 cm,△DEF的两边为DE=5 cm,EF=4 cm,则当DF=________cm时,△ABC∽△DEF.
15. 在平面直角坐标系中,A(2,0),B(1,2),A1(0,-4),B1(4,-2),则△AOB与△A1OB1的关系是________(填“相似”或“不相似”).
16. 如图,在△ABC中,AB=15,AC=8,在AC上取一点D,使AD=3,如果在AB上取一点E,使△ADE和△ABC相似,则AE的长为______________.
三.解答题(共6小题, 56分)
17.(6分) 如图,网格图中每个方格都是边长为1的正方形.若A,B,C,D,E,F都是格点,试说明△ABC∽△DEF.
18.(8分) .如图,在△ABC中,AB=25,BC=40,AC=20.在△ADE中,AE=12,AD=15,DE=24,试判断这两个三角形是否相似,并说明理由.
19.(8分) 如图,已知==,∠BAD=20°,求∠CAE的大小.
20.(10分) 根据下列条件,判断△ABC与△A′B′C′是否相似,并说明理由.
(1)AB=12,BC=15,AC=24,A′B′=25,B′C′=40,C′A′=20;
(2)AB=3,BC=4,AC=5,A′B′=12,B′C′=16,C′A′=20.
21.(12分) 如图,四边形ABCD,CDEF,EFGH都是边长相等的正方形.
(1)△ACF与△GCA相似吗?说说你的理由.
(2)求∠1+∠2的度数.
22.(12分) 如图,点B,D,E在一条直线上,BE与AC相交于点F,==.
(1)求证:∠BAD=∠CAE;
(2)若∠BAD=21°,求∠EBC的度数;
(3)连结EC,求证:△ABD∽△ACE.
参考答案
1-5DABCD 6-10BCCDD
11.△A″B″C″
12.∠CAE
13.,2
14.3
15.相似
16.或
17. 解:∵AC=,BC==,AB=4,DF==2,EF==2,ED=8,∴===,∴△ABC∽△DEF.
18. 解:相似.理由:∵==,==,==,∴==,∴△ABC∽△ADE
19.解:∵==,∴△ABC∽△ADE,∴∠BAC=∠DAE,又∠DAC是公共角,∴∠CAE=∠BAD=20°
20. 解:(1)△ABC与△A′B′C′相似.理由如下:∵==,==,==,∴==,∴△ABC ∽△C′A′B′.
(2)△ABC与△A′B′C′相似.理由如下:∵==,==,==,∴==,∴△ABC ∽△A′B′C′.
21. 解:(1)△ACF与△GCA相似.理由:可设正方形ABCD,CDEF,EFGH的边长为a,则△ACF的三边长分别为AC=a,CF=a,AF=a,△GCA的三边长分别为AC=a,CG=2a,AG=a.∴==,==,==.∴==.∴△ACF与△GCA相似.
(2)∵△ACF∽△GCA,∴∠1=∠CAF.∴∠1+∠2=∠CAF+∠2=∠ACB=45°.
22. 解:(1)∵==,∴△ABC ∽△ADE,∴∠BAC=∠DAE,∴∠BAC-∠DAF=∠DAE-∠DAF,∴∠BAD=∠CAE.
(2)∵△ABC ∽△ADE,∴∠ABC=∠ADE.∵∠ABC=∠ABE+∠EBC,∠ADE=∠ABE+∠BAD,∴∠EBC=∠BAD=21°.
(3)由(1)得∠BAD=∠CAE. 又∵=,∴△ABD ∽△ACE.
