14.1.4 整式的乘法(4) 课件(共25张PPT)
文档属性
| 名称 | 14.1.4 整式的乘法(4) 课件(共25张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-10 12:54:53 | ||
图片预览








文档简介
(共25张PPT)
14.1.4 整式的乘法(4)
人教版八年级上册
知识回顾
同底数幂相除,底数不变,指数相减.
符号表示:a0=1(a≠0).
1.同底数幂的除法性质:
符号表示:am÷an=am-n (a≠0,m,n都是正整数,并且m>n).
2.零指数幂的性质:
任何不等于0的数的零次幂都等于1.
教学目标
1.了解并掌握单项式除以单项式,多项式除以单项式的运算法则.
2.掌握单项式除以单项式,多项式除以单项式的运算法则的推导.
新知导入
(1)计算:4a2x3·3ab2= ;
(2)计算:12a3b2x3 ÷ 3ab2= .
12a3b2x3
4a2x3
12a3b2x3 ÷ 3ab2相当于求( )·3ab2=12a3b2x3.
由(1)可知括号里应填4a2x3.
即12a3b2x3 ÷ 3ab2=4a2x3.
单项式除以单项式
知识点 1
新知讲解
12a3b2x3÷3ab2=4a2x3.
观察上面的商式系数和字母的指数有什么特点?
上面的商式4a2x3的系数4=12÷3,
a的指数2=3-1,
b的指数0=2-2,而b0=1,
x的指数3=3-0.
你能总结出单项式与单项式相除的运算法则吗?
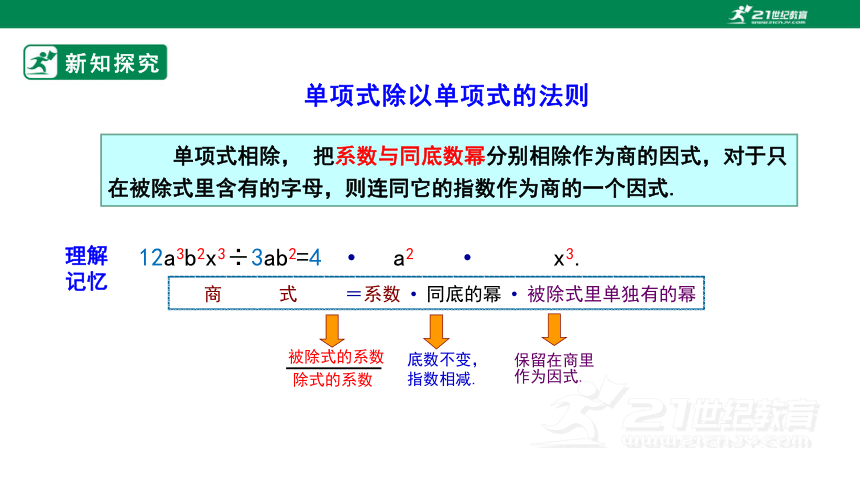
新知探究
单项式相除, 把系数与同底数幂分别相除作为商的因式,对于只在被除式里含有的字母,则连同它的指数作为商的一个因式.
理解记忆
商 式 =系数 同底的幂 被除式里单独有的幂
底数不变,
指数相减.
保留在商里
作为因式.
被除式的系数
除式的系数
单项式除以单项式的法则
12a3b2x3÷3ab2=4 a2 x3.
新知探究
注意:
(1) 单项式除以单项式时,注意单项式的系数应包括它前面的符号;
(2) 相同的单项式相除,结果是1而不是0;
(3) 不要遗漏只在被除式中出现而除式中没有的字母及字母的指数.
新知典例
例1 计算:
(1) 28x4y2÷7x3y; (2) -5a5b3c÷15a4b;
解:(1) 28x4y2÷7x3y
=(28÷7)·x4-3·y2-1
=4xy;
新知练习
1.下列计算是否正确?请将错误的结果改正?
(1)4a8 ÷2a 2= 2a 4 ( )
(2)10a3 ÷5a2=5a ( )
(3)(–9x5) ÷(–3x) =–3x4 ( )
(4)12a3b ÷4a2=3a ( )
2a6
2a
3x4
7ab
×
×
×
×
同底数幂的除法,底数不变,指数相减.
系数相除
求商的系数,应注意符号.
只在一个被除式里含有的字母,要连同它的指数写在商里,防止遗漏.
新知练习
2. 计算
(1)(2a2b2c)4z÷(–2ab2c2)2;
(2)(3x3y3z)4÷(3x3y2z)2÷x2y6z.
解:(1)原式=16a8b8c4z÷4a2b4c4=4a6b4z;
(2)原式=81x12y12z4÷9x6y4z2÷x2y6z=9x4y2z.
新知探究
多项式除以单项式
知识点 2
一幅长方形油画的长为(a+b),宽为m,求它的面积.
面积为(a+b)m=ma+mb.
长为(ma+mb)÷m.
问题1:
若已知油画的面积为(ma+mb),宽为m,如何求它的长?
问题2:
新知探究
如何计算(am+bm) ÷m
计算(am+bm) ÷m就相当于求( ) ·m=am+bm,因此不难推断出括里应填a+b.
问题3:
具体步骤
∵(a+b)m=am+bm,
∴(am+bm)÷m=a+b.
又am÷m+bm÷m=a+b,
∴(am+bm)÷m=am÷m+bm÷m.
你能总结出多项式与单项式相除的运算法则吗?
新知探究
一般地,多项式除以单项式,先把这个多项式的每一项除以这个单项式,再把所得的商相加.
符号表示:(am+bm)÷m=am÷m+bm÷m (a,b,m分别是单项式).
多项式除以单项式法则:
核心思想:应用法则是把多项式除以单项式转化为单项式除以单项式.
新知探究
注意:(1) 多项式除以单项式,被除式里有几项,商应该也有几项;
(2) 计算时,多项式的各项包括它前面的符号,要注意符号的变化.
(3)多项式除以单项式是单项式乘多项式的逆运算,因此可用单项式乘多项式检验多项式除以单项式的结果.
例如:
两项分别除以3a
指数相减
新知典例
例2 计算(12a3–6a2+3a) ÷3a.
解: (12a3–6a2+3a) ÷3a
=12a3÷3a+(–6a2) ÷3a+3a÷3a
=4a2+(–2a)+1
=4a2–2a+1
方法总结:多项式除以单项式,实质是利用乘法的分配律,将多项式除以单项式问题转化为单项式除以单项式问题来解决.计算过程中,要注意符号问题.
新知练习
3.计算:(1)(6x3y4z–4x2y3z+2xy3)÷2xy3;
(2)(72x3y4–36x2y3+9xy2)÷(–9xy2).
(2)原式= 72x3y4÷(–9xy2)+(–36x2y3)÷(–9xy2)+9xy2÷(–9xy2)
= –8x2y2+4xy–1
解:(1)原式=6x3y4z÷2xy3–4x2y3z÷2xy3+2xy3÷2xy3
=3x2yz–2xz+1
新知探究
例3 先化简,后求值:[2x(x2y–xy2)+xy(xy–x2)]÷x2y,其中x=2015,y=2014.
解:原式=[2x3y–2x2y2+x2y2–x3y]÷x2y,
原式=x–y=2015–2014=1.
=x–y.
把x=2015,y=2014代入上式,得
新知练习
4. 求值:(21x4y3–35x3y2+7x2y2)÷(–7x2y),其中x=1,y= –2
解:原式
=21x4y3 ÷(–7x2y) –35x3y2 ÷(–7x2y) +7x2y2 ÷(–7x2y)
= –3x2y2 + 5xy – y
把x=1,y=–2代入上式,得
课堂总结
整式的除法
同底数幂的除法
单项式除以单项式
底数不变,指数相减
1.系数相除;
2.同底数的幂相除;
3.只在被除式里的因式照搬作为商的一个因式
多项式除以单项式
转化为单项式除以单项式的问题
0指数幂的性质
除0以外任何数的0次幂都等于1
课堂练习
3. 已知一多项式与单项式–7x5y4 的积为21x5y7–28x6y5,则这个多项式是 .
–3y3+4xy
2.一个长方形的面积为a2+2a,若一边长为a,则另一边长为________.
a+2
1.已知28a3bm÷28anb2=b2,那么m,n的取值为( )
A.m=4,n=3 B.m=4,n=1
C.m=1,n=3 D.m=2,n=3
A
课堂练习
解:(1) (36a4-12a3-8a)÷(4a)
= 36a4÷(4a)+ (-12a3)÷(4a)+(-8a)÷(4a)
= 9a3-3a2-2 ;
4.计算下列式子:
(36a4-12a3-8a)÷(4a) ;
课堂练习
解:(2) (4xy4-2x2y3-8xy3z)÷2xy2
= 4xy4÷2xy2+ (-2x2y3)÷2xy2+(-8xy3z)÷2xy2
= 2x0-0y4-2-x2-1y3-2 -4x1-1y3-2z1-0
= 2y2-xy-4yz.
4.计算下列式子:
(2) (4xy4-2x2y3-8xy3z)÷(2xy2).
课堂练习
5.先化简,再求值:(x+y)(x–y)–(4x3y–8xy3)÷2xy,其中x=1,y=–3.
解:原式=x2–y2–2x2+4y2
原式=–12+3×(–3)2=–1+27=26.
当x=1,y=–3时,
=–x2+3y2.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
14.1.4 整式的乘法(4)
人教版八年级上册
知识回顾
同底数幂相除,底数不变,指数相减.
符号表示:a0=1(a≠0).
1.同底数幂的除法性质:
符号表示:am÷an=am-n (a≠0,m,n都是正整数,并且m>n).
2.零指数幂的性质:
任何不等于0的数的零次幂都等于1.
教学目标
1.了解并掌握单项式除以单项式,多项式除以单项式的运算法则.
2.掌握单项式除以单项式,多项式除以单项式的运算法则的推导.
新知导入
(1)计算:4a2x3·3ab2= ;
(2)计算:12a3b2x3 ÷ 3ab2= .
12a3b2x3
4a2x3
12a3b2x3 ÷ 3ab2相当于求( )·3ab2=12a3b2x3.
由(1)可知括号里应填4a2x3.
即12a3b2x3 ÷ 3ab2=4a2x3.
单项式除以单项式
知识点 1
新知讲解
12a3b2x3÷3ab2=4a2x3.
观察上面的商式系数和字母的指数有什么特点?
上面的商式4a2x3的系数4=12÷3,
a的指数2=3-1,
b的指数0=2-2,而b0=1,
x的指数3=3-0.
你能总结出单项式与单项式相除的运算法则吗?
新知探究
单项式相除, 把系数与同底数幂分别相除作为商的因式,对于只在被除式里含有的字母,则连同它的指数作为商的一个因式.
理解记忆
商 式 =系数 同底的幂 被除式里单独有的幂
底数不变,
指数相减.
保留在商里
作为因式.
被除式的系数
除式的系数
单项式除以单项式的法则
12a3b2x3÷3ab2=4 a2 x3.
新知探究
注意:
(1) 单项式除以单项式时,注意单项式的系数应包括它前面的符号;
(2) 相同的单项式相除,结果是1而不是0;
(3) 不要遗漏只在被除式中出现而除式中没有的字母及字母的指数.
新知典例
例1 计算:
(1) 28x4y2÷7x3y; (2) -5a5b3c÷15a4b;
解:(1) 28x4y2÷7x3y
=(28÷7)·x4-3·y2-1
=4xy;
新知练习
1.下列计算是否正确?请将错误的结果改正?
(1)4a8 ÷2a 2= 2a 4 ( )
(2)10a3 ÷5a2=5a ( )
(3)(–9x5) ÷(–3x) =–3x4 ( )
(4)12a3b ÷4a2=3a ( )
2a6
2a
3x4
7ab
×
×
×
×
同底数幂的除法,底数不变,指数相减.
系数相除
求商的系数,应注意符号.
只在一个被除式里含有的字母,要连同它的指数写在商里,防止遗漏.
新知练习
2. 计算
(1)(2a2b2c)4z÷(–2ab2c2)2;
(2)(3x3y3z)4÷(3x3y2z)2÷x2y6z.
解:(1)原式=16a8b8c4z÷4a2b4c4=4a6b4z;
(2)原式=81x12y12z4÷9x6y4z2÷x2y6z=9x4y2z.
新知探究
多项式除以单项式
知识点 2
一幅长方形油画的长为(a+b),宽为m,求它的面积.
面积为(a+b)m=ma+mb.
长为(ma+mb)÷m.
问题1:
若已知油画的面积为(ma+mb),宽为m,如何求它的长?
问题2:
新知探究
如何计算(am+bm) ÷m
计算(am+bm) ÷m就相当于求( ) ·m=am+bm,因此不难推断出括里应填a+b.
问题3:
具体步骤
∵(a+b)m=am+bm,
∴(am+bm)÷m=a+b.
又am÷m+bm÷m=a+b,
∴(am+bm)÷m=am÷m+bm÷m.
你能总结出多项式与单项式相除的运算法则吗?
新知探究
一般地,多项式除以单项式,先把这个多项式的每一项除以这个单项式,再把所得的商相加.
符号表示:(am+bm)÷m=am÷m+bm÷m (a,b,m分别是单项式).
多项式除以单项式法则:
核心思想:应用法则是把多项式除以单项式转化为单项式除以单项式.
新知探究
注意:(1) 多项式除以单项式,被除式里有几项,商应该也有几项;
(2) 计算时,多项式的各项包括它前面的符号,要注意符号的变化.
(3)多项式除以单项式是单项式乘多项式的逆运算,因此可用单项式乘多项式检验多项式除以单项式的结果.
例如:
两项分别除以3a
指数相减
新知典例
例2 计算(12a3–6a2+3a) ÷3a.
解: (12a3–6a2+3a) ÷3a
=12a3÷3a+(–6a2) ÷3a+3a÷3a
=4a2+(–2a)+1
=4a2–2a+1
方法总结:多项式除以单项式,实质是利用乘法的分配律,将多项式除以单项式问题转化为单项式除以单项式问题来解决.计算过程中,要注意符号问题.
新知练习
3.计算:(1)(6x3y4z–4x2y3z+2xy3)÷2xy3;
(2)(72x3y4–36x2y3+9xy2)÷(–9xy2).
(2)原式= 72x3y4÷(–9xy2)+(–36x2y3)÷(–9xy2)+9xy2÷(–9xy2)
= –8x2y2+4xy–1
解:(1)原式=6x3y4z÷2xy3–4x2y3z÷2xy3+2xy3÷2xy3
=3x2yz–2xz+1
新知探究
例3 先化简,后求值:[2x(x2y–xy2)+xy(xy–x2)]÷x2y,其中x=2015,y=2014.
解:原式=[2x3y–2x2y2+x2y2–x3y]÷x2y,
原式=x–y=2015–2014=1.
=x–y.
把x=2015,y=2014代入上式,得
新知练习
4. 求值:(21x4y3–35x3y2+7x2y2)÷(–7x2y),其中x=1,y= –2
解:原式
=21x4y3 ÷(–7x2y) –35x3y2 ÷(–7x2y) +7x2y2 ÷(–7x2y)
= –3x2y2 + 5xy – y
把x=1,y=–2代入上式,得
课堂总结
整式的除法
同底数幂的除法
单项式除以单项式
底数不变,指数相减
1.系数相除;
2.同底数的幂相除;
3.只在被除式里的因式照搬作为商的一个因式
多项式除以单项式
转化为单项式除以单项式的问题
0指数幂的性质
除0以外任何数的0次幂都等于1
课堂练习
3. 已知一多项式与单项式–7x5y4 的积为21x5y7–28x6y5,则这个多项式是 .
–3y3+4xy
2.一个长方形的面积为a2+2a,若一边长为a,则另一边长为________.
a+2
1.已知28a3bm÷28anb2=b2,那么m,n的取值为( )
A.m=4,n=3 B.m=4,n=1
C.m=1,n=3 D.m=2,n=3
A
课堂练习
解:(1) (36a4-12a3-8a)÷(4a)
= 36a4÷(4a)+ (-12a3)÷(4a)+(-8a)÷(4a)
= 9a3-3a2-2 ;
4.计算下列式子:
(36a4-12a3-8a)÷(4a) ;
课堂练习
解:(2) (4xy4-2x2y3-8xy3z)÷2xy2
= 4xy4÷2xy2+ (-2x2y3)÷2xy2+(-8xy3z)÷2xy2
= 2x0-0y4-2-x2-1y3-2 -4x1-1y3-2z1-0
= 2y2-xy-4yz.
4.计算下列式子:
(2) (4xy4-2x2y3-8xy3z)÷(2xy2).
课堂练习
5.先化简,再求值:(x+y)(x–y)–(4x3y–8xy3)÷2xy,其中x=1,y=–3.
解:原式=x2–y2–2x2+4y2
原式=–12+3×(–3)2=–1+27=26.
当x=1,y=–3时,
=–x2+3y2.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
