山东省济南市莱芜区雪野中心中学2022-2023学年六年级上学期段考数学试卷(五四学制)(01)(含答案)
文档属性
| 名称 | 山东省济南市莱芜区雪野中心中学2022-2023学年六年级上学期段考数学试卷(五四学制)(01)(含答案) | 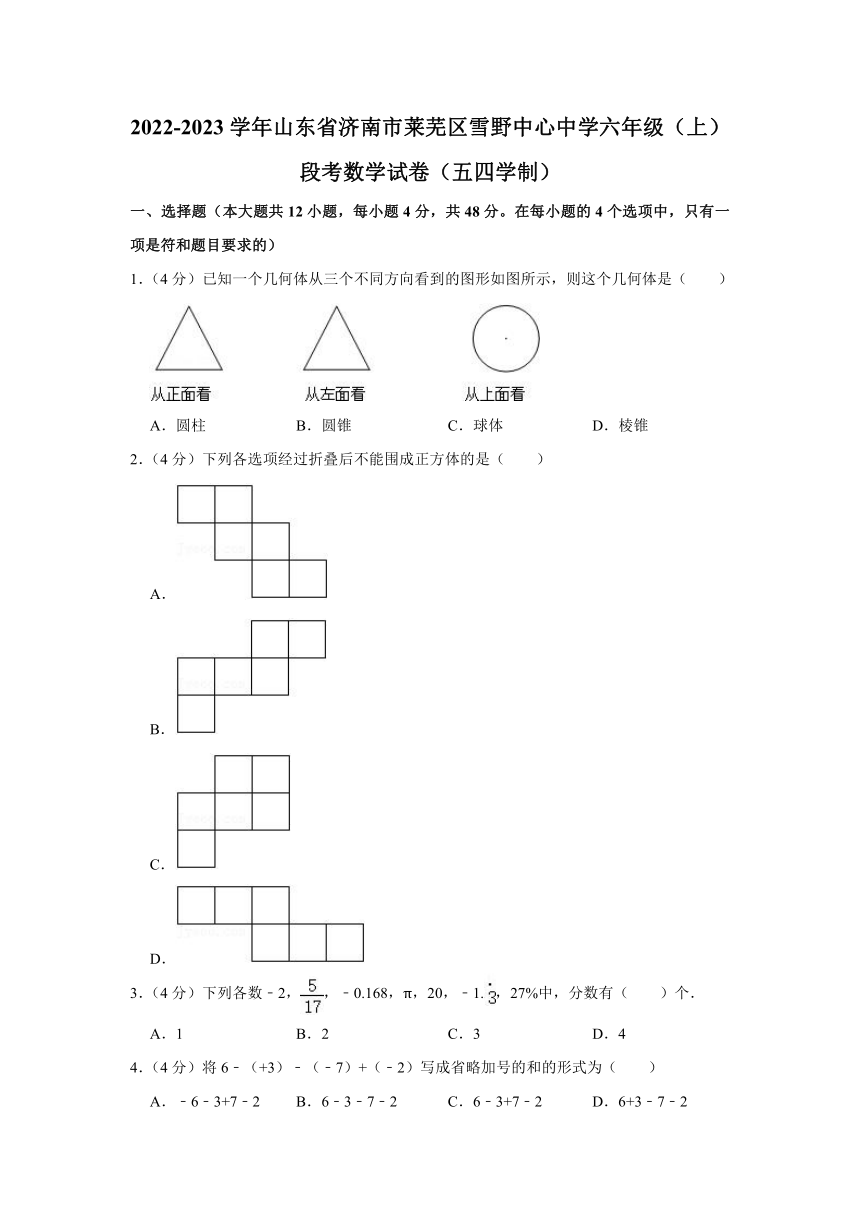 | |
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-10 19:49:24 | ||
图片预览




文档简介
2022-2023学年山东省济南市莱芜区雪野中心中学六年级(上)段考数学试卷(五四学制)
一、选择题(本大题共12小题,每小题4分,共48分。在每小题的4个选项中,只有一项是符和题目要求的)
1.(4分)已知一个几何体从三个不同方向看到的图形如图所示,则这个几何体是( )
A.圆柱 B.圆锥 C.球体 D.棱锥
2.(4分)下列各选项经过折叠后不能围成正方体的是( )
A.
B.
C.
D.
3.(4分)下列各数﹣2,,﹣0.168,π,20,﹣1.,27%中,分数有( )个.
A.1 B.2 C.3 D.4
4.(4分)将6﹣(+3)﹣(﹣7)+(﹣2)写成省略加号的和的形式为( )
A.﹣6﹣3+7﹣2 B.6﹣3﹣7﹣2 C.6﹣3+7﹣2 D.6+3﹣7﹣2
5.(4分)一种面粉的质量标识为“25±0.25千克”,则下列面粉中合格的是( )
A.24.70千克 B.25.30千克 C.24.80千克 D.25.51千克
6.(4分)下列关系一定成立的是( )
A.若|a|=|b|,则a=b B.若|a|=b,则a=b
C.若|a|=﹣b,则a=b D.若a=﹣b,则|a|=|b|
7.(4分)已知a、b、c在数轴上的位置如图所示,则下列结论正确的是( )
A.abc<0 B.|a|>|c| C.a﹣c>0 D.
8.(4分)如图是一个由多个相同小正方体堆积而成的几何体从上面看到的形状图,图中所示数字为该位置小正方体的个数,则这个几何体从正面看到的形状图是( )
A. B. C. D.
9.(4分)由若干个相同的小正方体组合而成的一个几何体的三视图如图所示,则组成这个几何体的小正方体的个数是( )
A.4 B.5 C.6 D.9
10.(4分)如图,在数轴上点A、B、C、D表示的数,其中绝对值最大的是( )
A.点A B.点B C.点C D.点D
11.(4分)若|x﹣2|=3,则x的值为( )
A.5 B.3或﹣5 C.3或﹣3 D.5或﹣1
12.(4分)若a,b互为相反数,则在①a+b=0,②a=﹣b,③|a|=|b|,④ab=﹣b2,⑤a2=b2中,一定成立的有( )
A.2个 B.3个 C.4个 D.5个
二、填空题(本大题共5小题,每小题4分,共20分)
13.(4分)如图所示,要使图中平面展开图折叠成正方体后,相对面上两个数之和为8,则x﹣y+z= .
14.(4分)一个水利勘察队,第一天向上游走5千米,第二天向上游走5千米,第三天向下游走4千米,第四天向下游走5千米,这时勘察队在出发点的上游 千米(规定上游为正).
15.(4分)如果数轴上的点A表示的有理数是﹣2,那么与点A相距5个单位长度的点所表示的有理数是 .
16.(4分)某年一月份,哈尔滨市的平均气温约为﹣20℃,绥化市的平均气温约为﹣23℃,则两地的温差为 ℃.
17.(4分)将一列有理数﹣1,2,﹣3,4,﹣5,6,…按如图所示的规律排列.根据图中的排列规律可知,“峰1”中峰顶的位置是有理数4,那么有理数﹣2019应排在A,B,C,D,E中 的位置.
三、解答题(共82分)
18.(12分)计算:
(1)5﹣(﹣2);
(2)|﹣|﹣|+|;
(3)5+(﹣1)+(﹣4);
(4)0﹣(﹣28)+53.
19.(6分)如图是由若干个小正方体搭成的几何体从上面看到的形状图,其中小正方形内的数字是该位置小正方体的个数,请分别画出从正面和从左面看到的形状图.
20.(16分)计算:
(1)(﹣7)﹣(﹣10)+(﹣8)﹣(+2);
(2)(﹣1.2)+[1﹣(﹣0.3)];
(3)(﹣4)﹣(+13)+(﹣5)﹣(﹣9)+7;
(4)6﹣3.3﹣(﹣6)﹣(﹣3)+4+3.3.
21.(8分)(1)13的相反数,加上﹣27的绝对值,再加上﹣31的和是多少?
(2)从﹣3中减去﹣与﹣的和,所得的差是多少?
22.(8分)已知|x+|+|y﹣|=0,求x+y的值.
23.(10分)随着科学技术的发展,信息化、网络化时代的到来,很多农产品改变了原来的销售模式,实行了网上销售,刚大学毕业的小韦把自己家的红薯产品也放到网上,他原来计划每天卖出150千克,由于各种原因,实际每天的销售量与计划量相比有出入,下表是国庆小长假期间的销售情况(超出部分记为正,不足记为负,单位:千克)
时间 1日 2日 3日 4日 5日 6日 7日
与计划量的差值 +12 ﹣5 ﹣7 +18 ﹣10 +17 ﹣8
(1)根据上表前四天一共卖出了多少千克?
(2)销售量最多的一天与最少的一天分别是多少千克?
(3)若每千克按2.6元出售,并需付运费平均每千克0.3元,则小韦国庆小长假期间一共收入多少钱?
24.(10分)根据如图所示的形状图(单位.:mm),求该几何体的体积.
25.(12分)已知在纸面上有一数轴,根据给出的数轴,解答下面的问题:
(1)请你根据图中A,B两点的位置,分别写出它们所表示的有理数;
(2)请问A,B两点之间的距离是多少?
(3)在数轴上画出与点A的距离为2的点(用不同于A.B的字母表示),并写出这些点表示的数;
(4)折叠纸面.若在数轴上﹣1对应的点与5对应的点重合,回答以下问题:
①10对应的点与 对应的点重合;
②若数轴上M、N两点之间的距离为2018(M在N的左侧),且M、N两总经折叠后重合,求M、N两点表示的数是多少;
(5)如图,半径为2的圆周上有一点Q落在数轴上A点处,求将圆在数轴上向右滚动(无滑动)一周后点Q在数轴上所表示的数.
2022-2023学年山东省济南市莱芜区雪野中心中学六年级(上)段考数学试卷(五四学制)
参考答案
一、选择题(本大题共12小题,每小题4分,共48分。在每小题的4个选项中,只有一项是符和题目要求的)
1.B 2.C 3.D 4.C 5.C 6.D
7.C 8.C 9.A 10.A 11.D 12.D
二、填空题(本大题共5小题,每小题4分,共20分)
13.答案为:3.
14.答案为:.
15.答案为:2或.
16.答案为3.
17.答案为:C.
三、解答题(共82分)
18.解:(1)5﹣(﹣2)
=5+2
=7;
(2)|﹣|﹣|+|
=﹣
=;
(3)5+(﹣1)+(﹣4)
=5﹣1﹣4
=0;
(4)0﹣(﹣28)+53
=28+53
=81.
19.解:图形如图所示:
20.解:(1)(﹣7)﹣(﹣10)+(﹣8)﹣(+2)
=﹣7+10﹣8﹣2
=﹣7+(10﹣8﹣2)
=﹣7+0
=﹣7;
(2)(﹣1.2)+[1﹣(﹣0.3)]
=﹣1.2+(1+0.3)
=﹣1.2+1.3
=0.1;
(3)(﹣4)﹣(+13)+(﹣5)﹣(﹣9)+7
=﹣4﹣13﹣5+9+7
=﹣22+16
=﹣6;
(4)6﹣3.3﹣(﹣6)﹣(﹣3)+4+3.3
=6.25﹣3.3+6+3.75+4+3.3
=6.25+3.75+6+4+3.3﹣3.3
=10+10
=20.
21.解:(1)根据题意得:﹣13+|﹣27|﹣31=﹣44+27=﹣17;
(2)根据题意得:﹣3﹣(﹣﹣)=﹣3++=﹣2.
22.解:∵|x+|+|y﹣|=0,
∴x+=0,y﹣=0,
∴x=﹣,y=,
∴x+y=﹣+
=﹣+
=﹣.
23.解:(1)前四天一共卖出了150×4+12﹣5﹣7+18=618(千克)
(2)销售最多的一天:150+18=168(千克)
销售最少的一天:150﹣10=140(千克)
(3)[(12﹣5﹣7+18﹣10+17﹣8)+7×150]×(2.6﹣0.3)
=1067×2.3
=2454.1(元)
答:小韦国庆小长假期间一共收入2454.1元.
24.解:这个几何体由两个圆柱组成,体积=π×42×4+π×82×16=1040π(mm2).
25.解:(1)两点表示的数为:A:1,B:﹣2.5;
(2)A、B两点之间的距离为1+2.5=3.5.
(3)在数轴上画出与点A的距离为2的点分别为3和﹣1,即数轴中C和D.
(4)①(﹣1+5)÷2=2,
2﹣(10﹣2)=﹣6.
故答案为:﹣6;
②∵M、N两点之间的距离为2018,
∴MN=×2018=1009,
对折点为2,
∴点M为2﹣1009=﹣1007,
点N为2+1009=1011.
(5)将圆在数轴上向右滚动(无滑动)一周后点Q所处的位置的点在数轴上所表示的数为4π+1.
一、选择题(本大题共12小题,每小题4分,共48分。在每小题的4个选项中,只有一项是符和题目要求的)
1.(4分)已知一个几何体从三个不同方向看到的图形如图所示,则这个几何体是( )
A.圆柱 B.圆锥 C.球体 D.棱锥
2.(4分)下列各选项经过折叠后不能围成正方体的是( )
A.
B.
C.
D.
3.(4分)下列各数﹣2,,﹣0.168,π,20,﹣1.,27%中,分数有( )个.
A.1 B.2 C.3 D.4
4.(4分)将6﹣(+3)﹣(﹣7)+(﹣2)写成省略加号的和的形式为( )
A.﹣6﹣3+7﹣2 B.6﹣3﹣7﹣2 C.6﹣3+7﹣2 D.6+3﹣7﹣2
5.(4分)一种面粉的质量标识为“25±0.25千克”,则下列面粉中合格的是( )
A.24.70千克 B.25.30千克 C.24.80千克 D.25.51千克
6.(4分)下列关系一定成立的是( )
A.若|a|=|b|,则a=b B.若|a|=b,则a=b
C.若|a|=﹣b,则a=b D.若a=﹣b,则|a|=|b|
7.(4分)已知a、b、c在数轴上的位置如图所示,则下列结论正确的是( )
A.abc<0 B.|a|>|c| C.a﹣c>0 D.
8.(4分)如图是一个由多个相同小正方体堆积而成的几何体从上面看到的形状图,图中所示数字为该位置小正方体的个数,则这个几何体从正面看到的形状图是( )
A. B. C. D.
9.(4分)由若干个相同的小正方体组合而成的一个几何体的三视图如图所示,则组成这个几何体的小正方体的个数是( )
A.4 B.5 C.6 D.9
10.(4分)如图,在数轴上点A、B、C、D表示的数,其中绝对值最大的是( )
A.点A B.点B C.点C D.点D
11.(4分)若|x﹣2|=3,则x的值为( )
A.5 B.3或﹣5 C.3或﹣3 D.5或﹣1
12.(4分)若a,b互为相反数,则在①a+b=0,②a=﹣b,③|a|=|b|,④ab=﹣b2,⑤a2=b2中,一定成立的有( )
A.2个 B.3个 C.4个 D.5个
二、填空题(本大题共5小题,每小题4分,共20分)
13.(4分)如图所示,要使图中平面展开图折叠成正方体后,相对面上两个数之和为8,则x﹣y+z= .
14.(4分)一个水利勘察队,第一天向上游走5千米,第二天向上游走5千米,第三天向下游走4千米,第四天向下游走5千米,这时勘察队在出发点的上游 千米(规定上游为正).
15.(4分)如果数轴上的点A表示的有理数是﹣2,那么与点A相距5个单位长度的点所表示的有理数是 .
16.(4分)某年一月份,哈尔滨市的平均气温约为﹣20℃,绥化市的平均气温约为﹣23℃,则两地的温差为 ℃.
17.(4分)将一列有理数﹣1,2,﹣3,4,﹣5,6,…按如图所示的规律排列.根据图中的排列规律可知,“峰1”中峰顶的位置是有理数4,那么有理数﹣2019应排在A,B,C,D,E中 的位置.
三、解答题(共82分)
18.(12分)计算:
(1)5﹣(﹣2);
(2)|﹣|﹣|+|;
(3)5+(﹣1)+(﹣4);
(4)0﹣(﹣28)+53.
19.(6分)如图是由若干个小正方体搭成的几何体从上面看到的形状图,其中小正方形内的数字是该位置小正方体的个数,请分别画出从正面和从左面看到的形状图.
20.(16分)计算:
(1)(﹣7)﹣(﹣10)+(﹣8)﹣(+2);
(2)(﹣1.2)+[1﹣(﹣0.3)];
(3)(﹣4)﹣(+13)+(﹣5)﹣(﹣9)+7;
(4)6﹣3.3﹣(﹣6)﹣(﹣3)+4+3.3.
21.(8分)(1)13的相反数,加上﹣27的绝对值,再加上﹣31的和是多少?
(2)从﹣3中减去﹣与﹣的和,所得的差是多少?
22.(8分)已知|x+|+|y﹣|=0,求x+y的值.
23.(10分)随着科学技术的发展,信息化、网络化时代的到来,很多农产品改变了原来的销售模式,实行了网上销售,刚大学毕业的小韦把自己家的红薯产品也放到网上,他原来计划每天卖出150千克,由于各种原因,实际每天的销售量与计划量相比有出入,下表是国庆小长假期间的销售情况(超出部分记为正,不足记为负,单位:千克)
时间 1日 2日 3日 4日 5日 6日 7日
与计划量的差值 +12 ﹣5 ﹣7 +18 ﹣10 +17 ﹣8
(1)根据上表前四天一共卖出了多少千克?
(2)销售量最多的一天与最少的一天分别是多少千克?
(3)若每千克按2.6元出售,并需付运费平均每千克0.3元,则小韦国庆小长假期间一共收入多少钱?
24.(10分)根据如图所示的形状图(单位.:mm),求该几何体的体积.
25.(12分)已知在纸面上有一数轴,根据给出的数轴,解答下面的问题:
(1)请你根据图中A,B两点的位置,分别写出它们所表示的有理数;
(2)请问A,B两点之间的距离是多少?
(3)在数轴上画出与点A的距离为2的点(用不同于A.B的字母表示),并写出这些点表示的数;
(4)折叠纸面.若在数轴上﹣1对应的点与5对应的点重合,回答以下问题:
①10对应的点与 对应的点重合;
②若数轴上M、N两点之间的距离为2018(M在N的左侧),且M、N两总经折叠后重合,求M、N两点表示的数是多少;
(5)如图,半径为2的圆周上有一点Q落在数轴上A点处,求将圆在数轴上向右滚动(无滑动)一周后点Q在数轴上所表示的数.
2022-2023学年山东省济南市莱芜区雪野中心中学六年级(上)段考数学试卷(五四学制)
参考答案
一、选择题(本大题共12小题,每小题4分,共48分。在每小题的4个选项中,只有一项是符和题目要求的)
1.B 2.C 3.D 4.C 5.C 6.D
7.C 8.C 9.A 10.A 11.D 12.D
二、填空题(本大题共5小题,每小题4分,共20分)
13.答案为:3.
14.答案为:.
15.答案为:2或.
16.答案为3.
17.答案为:C.
三、解答题(共82分)
18.解:(1)5﹣(﹣2)
=5+2
=7;
(2)|﹣|﹣|+|
=﹣
=;
(3)5+(﹣1)+(﹣4)
=5﹣1﹣4
=0;
(4)0﹣(﹣28)+53
=28+53
=81.
19.解:图形如图所示:
20.解:(1)(﹣7)﹣(﹣10)+(﹣8)﹣(+2)
=﹣7+10﹣8﹣2
=﹣7+(10﹣8﹣2)
=﹣7+0
=﹣7;
(2)(﹣1.2)+[1﹣(﹣0.3)]
=﹣1.2+(1+0.3)
=﹣1.2+1.3
=0.1;
(3)(﹣4)﹣(+13)+(﹣5)﹣(﹣9)+7
=﹣4﹣13﹣5+9+7
=﹣22+16
=﹣6;
(4)6﹣3.3﹣(﹣6)﹣(﹣3)+4+3.3
=6.25﹣3.3+6+3.75+4+3.3
=6.25+3.75+6+4+3.3﹣3.3
=10+10
=20.
21.解:(1)根据题意得:﹣13+|﹣27|﹣31=﹣44+27=﹣17;
(2)根据题意得:﹣3﹣(﹣﹣)=﹣3++=﹣2.
22.解:∵|x+|+|y﹣|=0,
∴x+=0,y﹣=0,
∴x=﹣,y=,
∴x+y=﹣+
=﹣+
=﹣.
23.解:(1)前四天一共卖出了150×4+12﹣5﹣7+18=618(千克)
(2)销售最多的一天:150+18=168(千克)
销售最少的一天:150﹣10=140(千克)
(3)[(12﹣5﹣7+18﹣10+17﹣8)+7×150]×(2.6﹣0.3)
=1067×2.3
=2454.1(元)
答:小韦国庆小长假期间一共收入2454.1元.
24.解:这个几何体由两个圆柱组成,体积=π×42×4+π×82×16=1040π(mm2).
25.解:(1)两点表示的数为:A:1,B:﹣2.5;
(2)A、B两点之间的距离为1+2.5=3.5.
(3)在数轴上画出与点A的距离为2的点分别为3和﹣1,即数轴中C和D.
(4)①(﹣1+5)÷2=2,
2﹣(10﹣2)=﹣6.
故答案为:﹣6;
②∵M、N两点之间的距离为2018,
∴MN=×2018=1009,
对折点为2,
∴点M为2﹣1009=﹣1007,
点N为2+1009=1011.
(5)将圆在数轴上向右滚动(无滑动)一周后点Q所处的位置的点在数轴上所表示的数为4π+1.
同课章节目录
