3.1.2 函数的表示法 课件-2022-2023学年高一上学期数学人教A版(2019)必修第一册(共38张PPT)
文档属性
| 名称 | 3.1.2 函数的表示法 课件-2022-2023学年高一上学期数学人教A版(2019)必修第一册(共38张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-10-10 00:00:00 | ||
图片预览









文档简介
(共38张PPT)
人教2019A版必修 第一册
3.1.2 函数的表示法
第三章 函数概念与性质
常用的有解析法、列表法和图象法三种.
⑴解析法:就是用数学表达式表示两个变量之间的对应关系.
如,s=60t2,A=r2,S=2,y=ax2+bx+c(a≠0),y=x+2等等都是用解析式表示函数关系的.3.1.1的问题1、2.
初中学过哪几种表示函数的方法
复习回顾
3.1.1问题1: 某 “复兴号”高速列车加速到350km/h后保持匀速运行半小时.这段时间内,列车行进的路程S(单位:km)与运行时间t(单位:h)的关系可以表示为:
解析法
.
常用的有解析法、列表法和图象法三种.
初中学过哪几种表示函数的方法
复习回顾
(2)图象法:就是用图象表示两个变量之间的对应关系.如3.1.1的问题3.
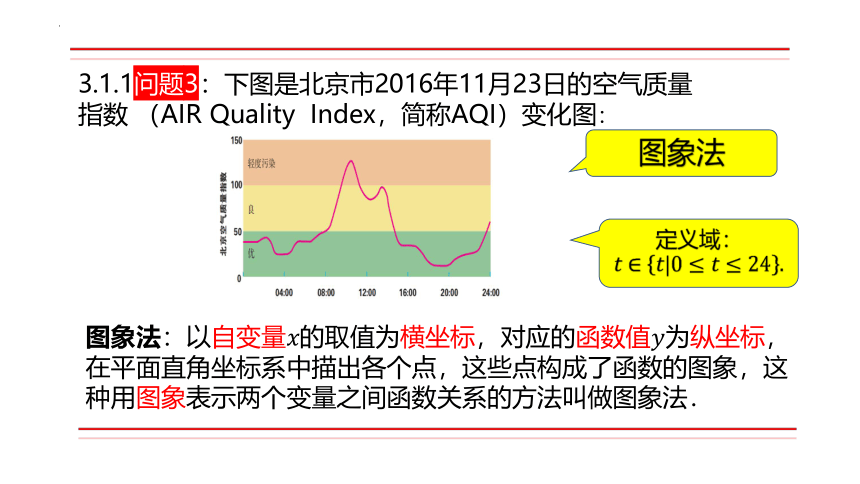
3.1.1问题3:下图是北京市2016年11月23日的空气质量指数 (AIR Quality Index,简称AQI)变化图:
图象法
定义域:
图象法:以自变量的取值为横坐标,对应的函数值为纵坐标,在平面直角坐标系中描出各个点,这些点构成了函数的图象,这种用图象表示两个变量之间函数关系的方法叫做图象法.
常用的有解析法、列表法和图象法三种.
初中学过哪几种表示函数的方法
复习回顾
(3)列表法:就是列出表格来表示两个变量之间的对应关系.如3.1.1的问题4.
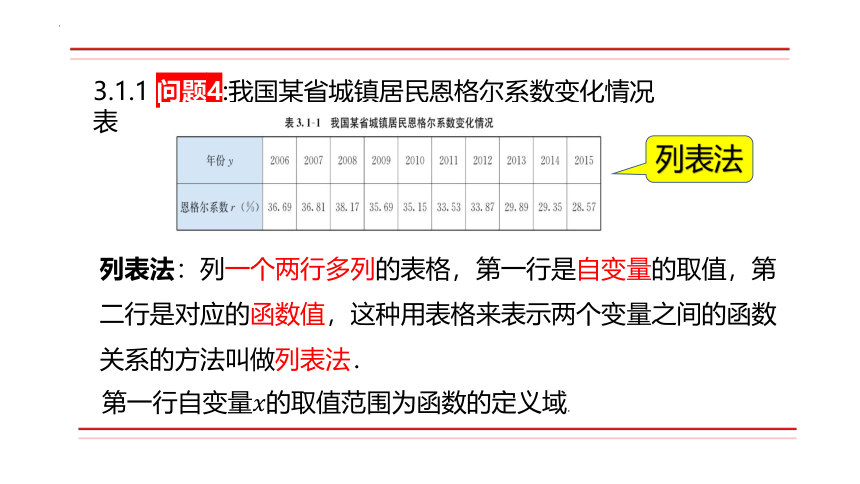
3.1.1 问题4:我国某省城镇居民恩格尔系数变化情况表
列表法
列表法:列一个两行多列的表格,第一行是自变量的取值,第二行是对应的函数值,这种用表格来表示两个变量之间的函数关系的方法叫做列表法.
第一行自变量的取值范围为函数的定义域.
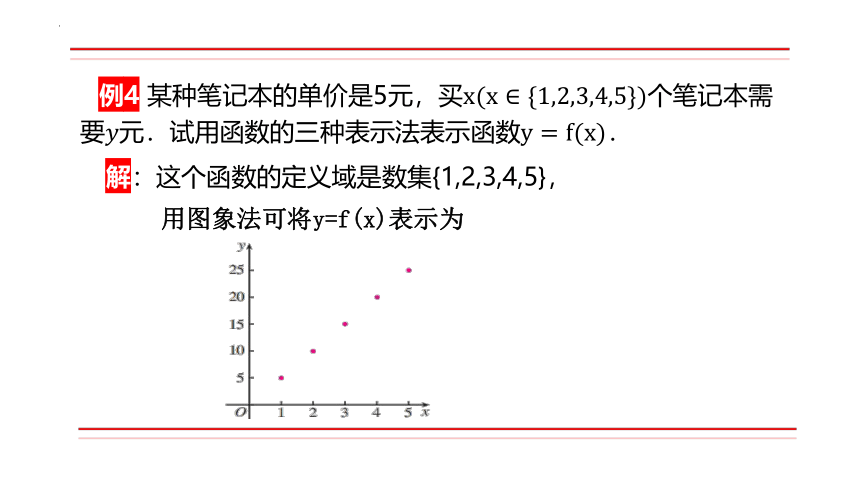
例4 某种笔记本的单价是5元,买个笔记本需要元.试用函数的三种表示法表示函数.
解:这个函数的定义域是数集{1,2,3,4,5},
用解析法可将函数表示为
.
用列表法可将函数表示为:
例4 某种笔记本的单价是5元,买个笔记本需要元.试用函数的三种表示法表示函数.
解:这个函数的定义域是数集{1,2,3,4,5},
用图象法可将y=f(x)表示为
解析法
①函数关系清楚、精确;
②容易从自变量的值求出其对应的函数值;③便于研究函数的性质.
解析法是中学研究函数的主要表达方法.
思考:比较三种表示法,它们各自的特点是什么?
简明、抽象、有规律.
图像法
思考:比较三种表示法,它们各自的特点是什么?
能形象直观的表示出函数的变化趋势,是今后利用数形结合思想解题的基础.
直观、趋势、不精准
列表法
思考:比较三种表示法,它们各自的特点是什么?
不必通过计算就知道当自变量取某些值时函数的对应值,当自变量的值的个数较少时使用.
列表法在实际生产和生活中有广泛的应用.
直观、离散.
不是所有的函数都能用解析法表示.
例如3.1.1问题3,某天24整点的整点数与这一刻的气温的关系.
思考:所有的函数都能用解析法表示吗?
解
例5. 画出函数y=|x| 的图象.
解: 由绝对值的概念,我们有
所以,函数y=|x| 的图象如图所示.
0
3
2
1
-1
-2
-3
1
2
3
4
我们把这样的函数
称为分段函数
以数化形
解析法抽象而精准,图象法直观而形象,二者相辅相成,能更好的理解这一函数,这就是所谓数形结合.
分段函数
1、分段函数:函数定义域分成若干区间段,在各个区间段内,
函数有不同的对应关系.
2、分段函数是一个函数,不是几个函数,分段函数的定义域
是各段函数定义域的并集.
分段函数
例6. 给定函数
(1)在同一直角坐标系中画出函数 的图象;
解:(1)在同一直角坐标系中画出函数 的图象,
如图。
例6. 给定函数
(2) 用M(x)表示 中的较大者,记为
请分别用图象法和解析法表示函数M(x).
解:由(1)中函数图象中函数取值的
情况,结合函数M(x)的定义,可
得函数M(x)的图象,如图
例6. 给定函数
结合函数的图象,
可得函数M(x)的解析式为
教材P69练习
教材P69练习
例7: 下表是某校高一(1)班三名同学在高一学年度六次数学测试的成绩及班级平均分表.
第一次 第二次 第三次 第三次 第五次 第六次
王伟 98 87 91 92 88 95
张城 90 76 88 75 86 80
赵磊 68 65 73 72 75 82
班级平均分 88.2 78.3 85.4 80.3 75.7 82.6
请你对这三位同学在高一学年度的数学学习情况做一个分析.
成绩
测试序号
姓名
解:从表中可以知道每位同学在每次测试中的成绩,但是不太容易看出每
位同学的成绩的变化情况.
可以将“成绩”与“测试序号”之间的关系用函数图像表示出来,如
图1,那么就能比较直观地看到成绩变化的情况.
1
3
2
4
x
0
5
6
60
y
70
80
90
100
王伟
张城
赵磊
班级平均分
图1
1
3
2
4
x
0
5
6
60
y
70
80
90
100
王伟
张城
赵磊
班级平均分
图2
为了更容易的看出学生的学习情况,将离散的点用虚线连接。
1
3
2
4
x
0
5
6
60
y
70
80
90
100
王伟
张城
赵磊
班级平均分
图2
在图2中看到,王伟同学的数学成绩始终高于班级平均水平,学习情况比较稳定而且比较优秀.张诚同学的数学成绩不稳定,总是在班级平均水平上下波动,而且幅度较大.赵磊同学的数学成绩低于平均水平,但是他的成绩呈曲线上升的趋势,从而表明他的数学成绩在稳步提高.
例8 依法纳税是每个公民应尽的义务,个人取得的所得应按照《中华人民共和国个人所得税法》向国家缴纳个人所得税(简称个税)。2019年1月1日起,个税税额根据应纳税所得额、税率和速算扣除数确定,计算公式为
个税税额=应纳税所得额×税率-速算扣除数 ①
应纳税所得额的计算公式为:
应纳税所得额=综合所得收入额-基本减除费用-专项扣除-专项附加扣除-依法确定的其他扣除 ②
其中,“基本减除费用”(免征额)为每年60000元。税率与速算扣除数见下表。
(1) 设全年应纳税所得额为t,应缴纳个税税额为y,
求 ,并画出图象。
解:(1) 根据上表,可得函数 的解析式为
③
函数图象如图所示
(2)小王全年综合所得收入额为189600元,假定缴纳的基本养老保险、基本医疗保险、失业保险等社会保险费和住房公积金占综合所得收入额的比例分别是8%,2%,1%,9%,专项附加扣除是52800元,依法确定其他扣除是4560元,那么他全年应缴纳多少综合所得个税?
解:根据公式②,小王全年应缴纳所得额为
t=189600-60000-189600(8%+2%+1%+9%)-52800-4560
=0.8×189600-117360=34320
将t的值代入③,得
y=0.03×34320=1029.6
所以,小王应缴纳的综合所得个税税额为1029.6元。
当堂训练
(1)理解函数的三种表示方法;
(2)在具体的实际问题中能够选用恰当的表示法来表示函数;
(3)注意分段函数的表示方法及其图象的画法;
课堂小结
人教2019A版必修 第一册
3.1.2 函数的表示法
第三章 函数概念与性质
常用的有解析法、列表法和图象法三种.
⑴解析法:就是用数学表达式表示两个变量之间的对应关系.
如,s=60t2,A=r2,S=2,y=ax2+bx+c(a≠0),y=x+2等等都是用解析式表示函数关系的.3.1.1的问题1、2.
初中学过哪几种表示函数的方法
复习回顾
3.1.1问题1: 某 “复兴号”高速列车加速到350km/h后保持匀速运行半小时.这段时间内,列车行进的路程S(单位:km)与运行时间t(单位:h)的关系可以表示为:
解析法
.
常用的有解析法、列表法和图象法三种.
初中学过哪几种表示函数的方法
复习回顾
(2)图象法:就是用图象表示两个变量之间的对应关系.如3.1.1的问题3.
3.1.1问题3:下图是北京市2016年11月23日的空气质量指数 (AIR Quality Index,简称AQI)变化图:
图象法
定义域:
图象法:以自变量的取值为横坐标,对应的函数值为纵坐标,在平面直角坐标系中描出各个点,这些点构成了函数的图象,这种用图象表示两个变量之间函数关系的方法叫做图象法.
常用的有解析法、列表法和图象法三种.
初中学过哪几种表示函数的方法
复习回顾
(3)列表法:就是列出表格来表示两个变量之间的对应关系.如3.1.1的问题4.
3.1.1 问题4:我国某省城镇居民恩格尔系数变化情况表
列表法
列表法:列一个两行多列的表格,第一行是自变量的取值,第二行是对应的函数值,这种用表格来表示两个变量之间的函数关系的方法叫做列表法.
第一行自变量的取值范围为函数的定义域.
例4 某种笔记本的单价是5元,买个笔记本需要元.试用函数的三种表示法表示函数.
解:这个函数的定义域是数集{1,2,3,4,5},
用解析法可将函数表示为
.
用列表法可将函数表示为:
例4 某种笔记本的单价是5元,买个笔记本需要元.试用函数的三种表示法表示函数.
解:这个函数的定义域是数集{1,2,3,4,5},
用图象法可将y=f(x)表示为
解析法
①函数关系清楚、精确;
②容易从自变量的值求出其对应的函数值;③便于研究函数的性质.
解析法是中学研究函数的主要表达方法.
思考:比较三种表示法,它们各自的特点是什么?
简明、抽象、有规律.
图像法
思考:比较三种表示法,它们各自的特点是什么?
能形象直观的表示出函数的变化趋势,是今后利用数形结合思想解题的基础.
直观、趋势、不精准
列表法
思考:比较三种表示法,它们各自的特点是什么?
不必通过计算就知道当自变量取某些值时函数的对应值,当自变量的值的个数较少时使用.
列表法在实际生产和生活中有广泛的应用.
直观、离散.
不是所有的函数都能用解析法表示.
例如3.1.1问题3,某天24整点的整点数与这一刻的气温的关系.
思考:所有的函数都能用解析法表示吗?
解
例5. 画出函数y=|x| 的图象.
解: 由绝对值的概念,我们有
所以,函数y=|x| 的图象如图所示.
0
3
2
1
-1
-2
-3
1
2
3
4
我们把这样的函数
称为分段函数
以数化形
解析法抽象而精准,图象法直观而形象,二者相辅相成,能更好的理解这一函数,这就是所谓数形结合.
分段函数
1、分段函数:函数定义域分成若干区间段,在各个区间段内,
函数有不同的对应关系.
2、分段函数是一个函数,不是几个函数,分段函数的定义域
是各段函数定义域的并集.
分段函数
例6. 给定函数
(1)在同一直角坐标系中画出函数 的图象;
解:(1)在同一直角坐标系中画出函数 的图象,
如图。
例6. 给定函数
(2) 用M(x)表示 中的较大者,记为
请分别用图象法和解析法表示函数M(x).
解:由(1)中函数图象中函数取值的
情况,结合函数M(x)的定义,可
得函数M(x)的图象,如图
例6. 给定函数
结合函数的图象,
可得函数M(x)的解析式为
教材P69练习
教材P69练习
例7: 下表是某校高一(1)班三名同学在高一学年度六次数学测试的成绩及班级平均分表.
第一次 第二次 第三次 第三次 第五次 第六次
王伟 98 87 91 92 88 95
张城 90 76 88 75 86 80
赵磊 68 65 73 72 75 82
班级平均分 88.2 78.3 85.4 80.3 75.7 82.6
请你对这三位同学在高一学年度的数学学习情况做一个分析.
成绩
测试序号
姓名
解:从表中可以知道每位同学在每次测试中的成绩,但是不太容易看出每
位同学的成绩的变化情况.
可以将“成绩”与“测试序号”之间的关系用函数图像表示出来,如
图1,那么就能比较直观地看到成绩变化的情况.
1
3
2
4
x
0
5
6
60
y
70
80
90
100
王伟
张城
赵磊
班级平均分
图1
1
3
2
4
x
0
5
6
60
y
70
80
90
100
王伟
张城
赵磊
班级平均分
图2
为了更容易的看出学生的学习情况,将离散的点用虚线连接。
1
3
2
4
x
0
5
6
60
y
70
80
90
100
王伟
张城
赵磊
班级平均分
图2
在图2中看到,王伟同学的数学成绩始终高于班级平均水平,学习情况比较稳定而且比较优秀.张诚同学的数学成绩不稳定,总是在班级平均水平上下波动,而且幅度较大.赵磊同学的数学成绩低于平均水平,但是他的成绩呈曲线上升的趋势,从而表明他的数学成绩在稳步提高.
例8 依法纳税是每个公民应尽的义务,个人取得的所得应按照《中华人民共和国个人所得税法》向国家缴纳个人所得税(简称个税)。2019年1月1日起,个税税额根据应纳税所得额、税率和速算扣除数确定,计算公式为
个税税额=应纳税所得额×税率-速算扣除数 ①
应纳税所得额的计算公式为:
应纳税所得额=综合所得收入额-基本减除费用-专项扣除-专项附加扣除-依法确定的其他扣除 ②
其中,“基本减除费用”(免征额)为每年60000元。税率与速算扣除数见下表。
(1) 设全年应纳税所得额为t,应缴纳个税税额为y,
求 ,并画出图象。
解:(1) 根据上表,可得函数 的解析式为
③
函数图象如图所示
(2)小王全年综合所得收入额为189600元,假定缴纳的基本养老保险、基本医疗保险、失业保险等社会保险费和住房公积金占综合所得收入额的比例分别是8%,2%,1%,9%,专项附加扣除是52800元,依法确定其他扣除是4560元,那么他全年应缴纳多少综合所得个税?
解:根据公式②,小王全年应缴纳所得额为
t=189600-60000-189600(8%+2%+1%+9%)-52800-4560
=0.8×189600-117360=34320
将t的值代入③,得
y=0.03×34320=1029.6
所以,小王应缴纳的综合所得个税税额为1029.6元。
当堂训练
(1)理解函数的三种表示方法;
(2)在具体的实际问题中能够选用恰当的表示法来表示函数;
(3)注意分段函数的表示方法及其图象的画法;
课堂小结
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
